不同插值方法的比较

1.多项式插值

多项式插值：以一个多项式的形式来刻画经过一系列点的曲线。

拉格朗日插值：简单易用，即每增加一个新的插值点时，整个基函数就需要重新构建，这大大增加了运算量。为此，我们需要寻找一种新的基函数，其能够在节点增加时，只需要在原有的基函数上增加一些新的基函数即可，而无需对原始的基函数进行重构。
牛顿插值：也是n次多项式插值，是构造插值多项式的另一种方法，它具有继承性和易变化节点的特点。该基函数的一个优点是当增加一个新的插值节点 时，只需在原有基函数的基础上增加一个新的函数即可。

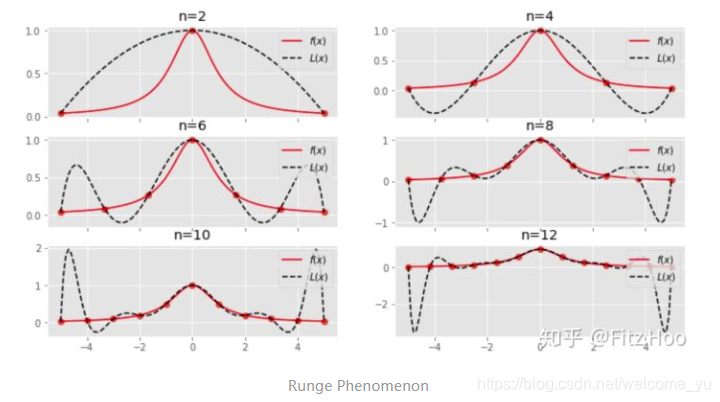
龙格现象：
在一组等间距插值点上使用具有高次多项式进行插值时出现的区间边缘处震荡问题。
随着节点数逐渐在增加，插值精度不断提升，但插值曲线也开始在边缘处变得不够稳定。

2.分段插值

为了避免高次插值多项式的缺陷，得到 较好的近似式, 一般采用分段插值法，即把插值区间 分为若干个子区间，在每个子区间上构造低次插值多项式.

常见的分段插值主要有分段线性插值，三次Hermite插值以及三次样条插值。
分段线性插值：
分段线性插值利用每两个相邻的插值基点组线性插值。
分段低次插值有效地避免了龙格现象, 同时其截断误差也得到了有效的控制, 总体是比较稳定的。
但其缺点在于插值条件仅限定函数值在节点处相等，这仅能保证插值函数的连续性, 总体的光滑性不高，若需要得到光滑性更好的插值函数, 我们需要对函数的导数进行约束。
三次Hermite插值：
三次样条插值：用分段插值方法绘制通过节点的曲线，龙格现象消失。
分段插值时，节点的选择对插值结果会有显著的影响。

更多详细内容及相关代码：
https://zhuanlan.zhihu.com/p/63763725