本文深入探讨旅行商问题(TSP)，解释其作为组合优化问题的数学模型，阐述计算复杂度，并详细介绍了三种求解方法：暴力枚举、动态规划和回溯。通过对每种方法的原理和实现进行讲解，揭示了解决TSP问题的思路。
旅行商问题(TSP)
1 简介
旅行商问题属于组合优化问题。
组合优化问题(Combinatorial Optimization Problem，COP)是一类在离散状态下求极值的问题。把某种离散对象按某个确定的约束条件进行安排，当已知合乎这种约束条件的特定安排存在时寻求这种特定安排在某个优化准则下的极大解或极小解。
TSP 的经典提法是：有一个销售员要去若干个城市销售货品，从某个固定城市出发(假设每个城市之间的距离固定)，经过剩下的每个城市至少一次，然后回到起始城市，问题是选择哪条线路，才能使总行程最短。
该问题在图论意义下就是所谓的 Hamilton 圈问题。
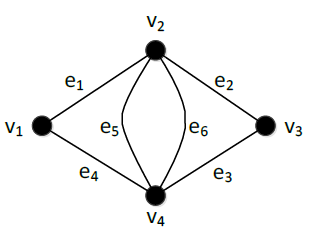
上图展示的是一个无向图 G，假设从任意一个顶点出发，剩下每一个顶点恰好遍历一次，最后回到原点
订阅专栏 解锁全文
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
