初中数学:绝对式和的最小值

一,引入

初中生学了绝对值后，会经常遇到一个类型题，求一个式子绝对值的最小值。形如│x-a│，因当x无限大时，式子的绝对值也无限大，而绝对值是一个非负数，所以式子的绝对值最小为0，此时，x=a。所以，绝对值的最小值是经常考察的一个知识点。接下我们就总结一下绝对值最小值的类型题。

---

二、求绝对式和的最小值

首先我们要了解绝对值的几何含义。一个数的绝对值表示这个数在数轴上到原点的距离。两个数差的绝对值表示两个数在数轴上间的距离。计算方法是大数减小数。

1.绝对值的几何含义

若 a<0, b>0,且 │a│<│ b│,有:
│a│=0-a =-a, │ b│=b-0=b，│b-a│=b-a, │a-b│=b-a。

形如│a+b│，我们可以看作为│a+b│=│a-(-b)│=a-(-b)=a+b。即遇到相加的形式，写成减的形式,构造绝对值的几何意义。

2、两个绝对式的和

形如│x-a│+│x-b│，（a>b）求它的最小值。

（1）当x在b的左边时

│x-a│+│x-b│=线段xb长+线段xa长>线段ab长。

（2）当x在b上时

│x-a│+│x-b│=0+线段ab长=线段ab长。

（3）当x在a,b之间时

│x-a│+│x-b│=线段xb长+线段ax长=ab长。

（4）当x在a上时

│x-a│+│x-b│=线段xb长+0=线段ab长。

（5）当x在a的右边时

│x-a│+│x-b│=线段xb长+线段xa长>线段ab长。

通过上面分析，可知:

当 b≤x≤a时， │x-a│+│x-b│是 最小值，长度为 线段ab长=a-b。

练习

1.

请问│x-3│+│x-8│=多少?

ans:│x-3│+│x-8│=8-3=5

2.

请问│x-3│+│x+8│=多少?

ans:│x-3│+│x+8│=3-（-8）=11

3、三个绝对式的和

形如│x-a│+│x-b│+│x-c│，（a>b>c）,求它的最小值。

进过上面分析，我们已经知道│x-a│+│x-c│的最小值为a-c，那么只需确定│x-b│的最小值就可以了。当x=b时，│x-b│最小为0。

所以:

当且仅当x=b时， │x-a│+│x-b│+│x-c│为最小值， 最小值为a-c。

练习

│x-5│+│x-8│+│x-10│=?。

ans:│x-5│+│x-8│+│x-10│=10-5=5

4、四个绝对式的和

形如│x-a│+│x-b│+│x-c│+│x-d│，（a>b>c>d）,求它的最小值。

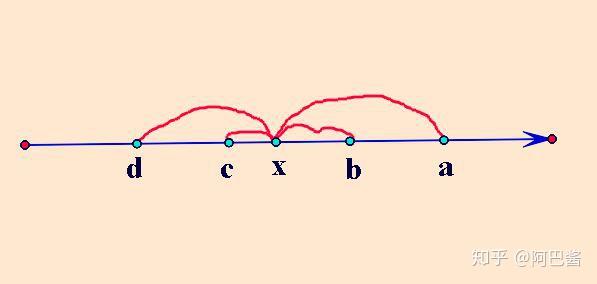
综上分析，我们可知│x-a│+│x-d│有最小值为a-d，│x-b│+│x-c│有最小值为b-c。

所以:

│x-a│+│x-b│+│x-c│+│x-d│的 最小值就为a-d+b-c= a+b-c-d。

5、五个绝对式的值

形如│x-a│+│x-b│+│x-c│+│x-d│+│x-e│，（a>b>c>d>e）,求它的最小值。

综上分析，我们可知│x-a│+│x-e│有最小值为a-e，│x-b│+│x-d│有最小值为b-d,现在只需使│x-c│最小即可。由此可知当且仅当x=c时，，

│x-a│+│x-b│+│x-c│+│x-d│+│x-e│为最小值:a-e+b-d= a+b-e-d。

6,结论

通过以上分析，我们可以得出形如│x-a│+│x-b│+│x-c│+│x-d│+......的最小值的求解方法。

（1）将每个绝对式的形式写成│x-a│的形式。

（2）将各个数它按从大到小排列（从小到大也可以）。

（3）若绝对式的个数是偶数个，可以将数按排列顺序分成相等的两部分，用前面数的和减去后面数的和，就是所求结果。

（4）若绝对式的个数是奇数个，将数按最中间的数为分界点，前面的数分为一部分，后面的数分为一部分，用前面数的后，减去后面数的后，就是所求结果。

也就是

---

三，结语

好了，关于绝对式的和就讲到这里。喜欢的朋友可以关注+点赞+收藏哦,我会不定期与你分享数学和编程知识。bye~bye~

末尾有彩蛋你信吗

---

---

---

---

---

---

---

---

---

---

---

---

---

---

四，彩蛋(不喜勿看)

hhh,恭喜你，喜提我精心准备的举一反三的练习题一份!(附讲解)

1. 例题1

|x-3|+2*|x+5|+3*|x-7|,要使这个算式最小,x的范围是___~___？

ans:

其实很简单,把乘改成加,再套公式即可。

|x-3|+2*|x+5|+3*|x-7|

=|x-3|+2*|x-(-5)|+3*|(x-7)|

=|x-3|+|x-(-5)|+|x-(-5)|+|(x-7)|+|(x-7)|+|(x-7)|

那么此时n为偶数，所以此时将数组{3,-5,-5,7,7,7}排一下序变成{-5,-5,3,7,7,7},

中间的2个数为3,7,所以答案为:x的范围是3~7

1. 例题2

|x-3|+|2x+5|+ |3x-7|,要使这个算式最小,x的范围是___~___？

ans:

上一题的举一反三,将x前面乘的系数移到绝对值符号外即可。

|x-3|+|2x+5|+ |3x-7|

=|x-3|+2*|x+(5/2)|+3*|x-(7/3)|

=|x-3|+|x+(5/2)|+|x+(5/2)|+|x-(7/3)|+|x-(7/3)|+|x-(7/3)|

那么此时n为偶数，所以此时将数组{3,5/2,5/2,7/3,7/3,7/3}排一下序变成{7/3,7/3,7/3,5/2,5/2,3},

中间的2个数为7/3,5/2,所以答案为:x的范围是7/3~5/2

如果本蒟蒻的文章某处有误请各位大佬们在评论区指正,谢谢!

真的没有了!