数据分析模型 第五章

一. 假设检验(Hypothesis Testing)

看到第五章，可能大家会有两个问题:
1.是否我们的参数等于一个具体的数值么？
2.如果有多个模型是否，其中某一个模型更能诠释我们的数据.
本章我们就讨论下第一个问题
假设检验(Hypothesis Testing)通常应用在参数的估计上。这个词，很明显，我们假设是否我们的真参等于某个数值，然后进行检验是否我们的原假设正确.
先介绍下假设检验写法:

                    $H_0:$ 原假设（虚假设,0假设,null hypothesis）

                        $VS$

                   $H_1:$ 对立假设（备择假设,alternative hypothesis）

啥意思？我们随便写一个：
假如我们这里有个总体一大把数据服从正态分布
那么我们假设检验的写法:
                    $H_0:$ $\mu ={\mu }_0$

                        $VS$

                    $H_1:$ $\mu \ne {\mu }_0$

根据上述写法，原假设$H_0:$ $\mu ={\mu }_0$，对立假设$H_1:$ $\mu \ne {\mu }_0$原假设的反面.于是我们会问自己，是否我们的样本数据可以证明我们的假设是否$\mu$等于一个具体的固定的数值${\mu }_0$?
这里有两点核心在假设检验中:
1.我们假想原假设是正确的
2.我们利用样本的数据来计算概率来证明是否我们的原假设正确，概率(p-值)越小，说明样本数据提供大量的证据来反对我们的原假设.
这两句话很抽象，没事，来个简单的例题理解下.

例题:
假如我们的总体服从$N(\mu ,{\sigma }^2)$,$\mu$未知，${\sigma }^2$已知。${\mu }_0$是我们猜的一个具体的数值并认为$\mu ={\mu }_0$.
那么我们的测试写成:
                    $H_0:$ $\mu ={\mu }_0$

                        $VS$

                    $H_1:$ $\mu \ne {\mu }_0$
我们的任务使利用样本来判断是否原假设成立。

错解:
给大家做个错误的做法，可能有很多同学会进入这个误区.
假如抽取一组样本$Y_1,Y_2,...,Y_n$从我们的总体中，如果这道题抛开假设检验不谈，我们是不是发现，这题怎么跟算置信区间很像。根据我们第四章，我们知道$Y_1,Y_2,...,Y_n～N(\mu ,{\sigma }^2)$，也知道${\bar{\mu }}_{ML}=\bar{Y}=\frac{1}{n}{\sum }_{i=1}^n{Y}_i～N(\mu ,\frac{{\sigma }^2}{n})$，$({\bar{\mu }}_{ML}-\mu )/(\sigma \sqrt{n})～N(0,1)$,取95%，那么估计$\mu$的置信区间为 P { μ ˉ M L − 1.96 σ n < μ < μ ˉ M L + 1.96 σ n } = 0.95 P\{ \bar \mu_{ML}-1.96\frac{\sigma}{\sqrt n}<\mu<\bar \mu_{ML}+1.96\frac{\sigma}{\sqrt n}\}=0.95 P{μˉ​ML​−1.96n ​σ​<μ<μˉ​ML​+1.96n ​σ​}=0.95这个结论的含义是我们有95%的自信度，真参$\mu$落在这个区间里. 现在我们在把假设检验也思考进去，因为我们猜$\mu ={\mu }_0$(原假设),那我们希望${\mu }_0$在这个置信区间内.如果不在这个置信区间内，则原假设错误。
这样做对么？很明显不对，为什么，不要忘了，我们取的样本是有很大的随机性的，点估计有很大随机性.正如第四章内容:

假如我们原假设$H_0:\mu =1.65$，因为取样一次算点估计，取得样本为(1.70,1.10,1.53,0.90)得到95%置信区间(0.997,1.617), $\mu =1.65$不在区间内。但你能说他错么？1.65这不就是真参的具体值么，但我们却把原假设定义为错的.

正解：我们要利用p值来判断是否原假设成立!!!

p值(p-value)
p值是由费雪大哥想出来的，虽然p-值饱受争议，但放心，它的争议跟我们涉及使用它没半毛关系。争议主要在于哲学的思考上面，对于由p值引申的学术研究有着思考方向性的影响.
讲p值之前，小弟和大家讲个笑话：天气预报说明天80%概率晴天，1%的概率天上掉钱，5%的概率天上掉饼，4%概率天上掉外星人，5%冰雹，3%沙尘暴…

这个笑话其实挺严肃的，如果在我们心里10%以下概率认为根本不会发生，那么是不是无论有多么不可能，明天我们还是挺期待的，因为除了晴天，还有20%的概率会有些乱七八糟的事情们可能会发生.这20%我们可以把它当作p值，而这p值超出了我们心里认为的10%概率的根本不会发生事件。

这种想法在某种程度上弥补了我们上述点估计的随机性，弥补了原假设$H_0:\mu =1.65$我们会把它当错。因为无论多荒唐的事情，他们累加到一起发生的概率其实还是很可观的，所以发生什么事情其实都不需要很惊讶的。所以p值其实是观察数据后，所有极端的结果出现的概率。

接着上述例题，我们已知$Z=({\bar{\mu }}_{ML}-\mu )/(\sigma \sqrt{n})～N(0,1)$,那么如果我们假设成立，那么我们的$z_{{\bar{\mu }}_{ML}}=({\bar{\mu }}_{ML}-{\mu }_0)/(\sigma \sqrt{n})～N(0,1)$,这个公式用在假设检验里时，也叫z-score，另外我们也知道${\bar{\mu }}_{ML}=\bar{Y}=\frac{1}{n}{\sum }_{i=1}^n{Y}_i～N(\mu ,\frac{{\sigma }^2}{n})$。

我们具体来看看z-score 公式（测试统计数据(Test statistic,z score)）
$$z_{{\bar{\mu }}_{ML}}=({\bar{\mu }}_{ML}-{\mu }_0)/(\sigma \sqrt{n})～N(0,1)$$
根据标准正态分布，上述z-score公式的分子$({\bar{\mu }}_{ML}-{\mu }_0)$描述了我们的点估计和我们假设的${\mu }_0$之间的差距，分母$(\sigma \sqrt{n})$是标准方差，那么这个公式其实在讲，点估计和我们假设的${\mu }_0$之间差了有多少个标准方差。

我们之前也提到了，点估计${\bar{\mu }}_{ML}$怎么着也不会完全等于${\mu }_0$，即使我们假设正确$\mu ={\mu }_0$. 举个例子，真参平均身高1.7米，你原假设猜中了，但你抽的样本很背，抽到样本均值身高2米，但其实这种极端情况我们是可以接受的，并也会证明你的原假设没问题。但如果你抽的样本均值身高100米，这我们就不能接受了，你思考的不仅仅是你原假设有问题了，你该思考我在研究什么了。

再者，根据上述观点，我们做假设检验的时候，我们其实是在问自己:根据样本数据得到的${\bar{\mu }}_{ML}$来证明$\mu ={\mu }_0$有多么不成立，也就是说我们其实本质上是反对原假设的，站在反对原假设，支持备择假设的立场来证明的。因为备择假设$\mu \ne {\mu }_0$,所以在$Z=({\bar{\mu }}_{ML}-\mu )/(\sigma \sqrt{n})～N(0,1)$中，为这个标准正态分布的两小端，概率低，所以这两端地方对应的${\mu }_0$可以认为是不等于$\mu$的. 有的同学会讲，那既然如此，为什么不能把写原假设为$H_0：\mu \ne {\mu }_0$，备择假设写为$H_1：\mu ={\mu }_0$.这个问题小弟当时问过老师，老师原话是这是书写习惯。

因为备择假设$\mu \ne {\mu }_0$,所以在$Z=({\bar{\mu }}_{ML}-\mu )/(\sigma \sqrt{n})～N(0,1)$中，为这个标准正态分布的两小端,这两小段的概率很低并且离我们认为的真参$\mu$相差甚远，所以再回到$z_{{\bar{\mu }}_{ML}}$这个公式，我们要考虑正方向和反方向即$\pm |z_{{\bar{\mu }}_{ML}}|$，如果${\bar{\mu }}_{ML}$比${\mu }_0$大，那么差多少个标准差，如果${\bar{\mu }}_{ML}$比${\mu }_0$小，那么差多少个标准差，这其实也是标准正态分布的特点. 所以无论正差还是负差，差越大，越不好，毕竟$({\bar{\mu }}_{ML}-{\mu }_0)$我们的点估计和我们假设的${\mu }_0$之间的差距越来越大，越不像。但记住，如果把他们累加到一起，他们的概率发生还是很可观的。那么它们所有加一起的概率可以写成:
p = p 值 = 1 − P ( − ∣ z μ ˉ M L ∣ < Z < + ∣ z μ ˉ M L ∣ ) = 2 P { Z < − ∣ z μ ˉ M L ∣ } p=p值=1-P(-|z_{\bar \mu_{ML}}|<Z<+|z_{\bar \mu_{ML}}|)=2P\{Z<-|z_{\bar \mu_{ML}}|\} p=p值=1−P(−∣zμˉ​ML​​∣<Z<+∣zμˉ​ML​​∣)=2P{Z<−∣zμˉ​ML​​∣}
这就是我们的p值，这里的$Z=({\bar{\mu }}_{ML}-\mu )/(\sigma \sqrt{n})～N(0,1)$， 2 P { Z < − ∣ z μ ˉ M L ∣ } 2P\{Z<-|z_{\bar \mu_{ML}}|\} 2P{Z<−∣zμˉ​ML​​∣}，x2因为正态分布的对称性. $z_{{\bar{\mu }}_{ML}}$叫 测试统计数据(Test statistic,z score)也叫z-score。 于是我们可以根据给的表格算出p值，学校里都会给计算p值的表格吧?!

但现在有个问题，现在有p值了，那多少才算发生这些事情的概率很可观呢，对没错利用95%的置信区间，很久以前费雪大哥给p值定义了一个特殊的概率阈值，根据人类的认知。但为了统一，就利用95%的置信区间的P{Z<-1.96}和P{Z>1.96}作为阈值了。啥是阈值，阈值就是个界.但我们不能把它想成坐标里的一个点，应该是一小段概率。

如下图:

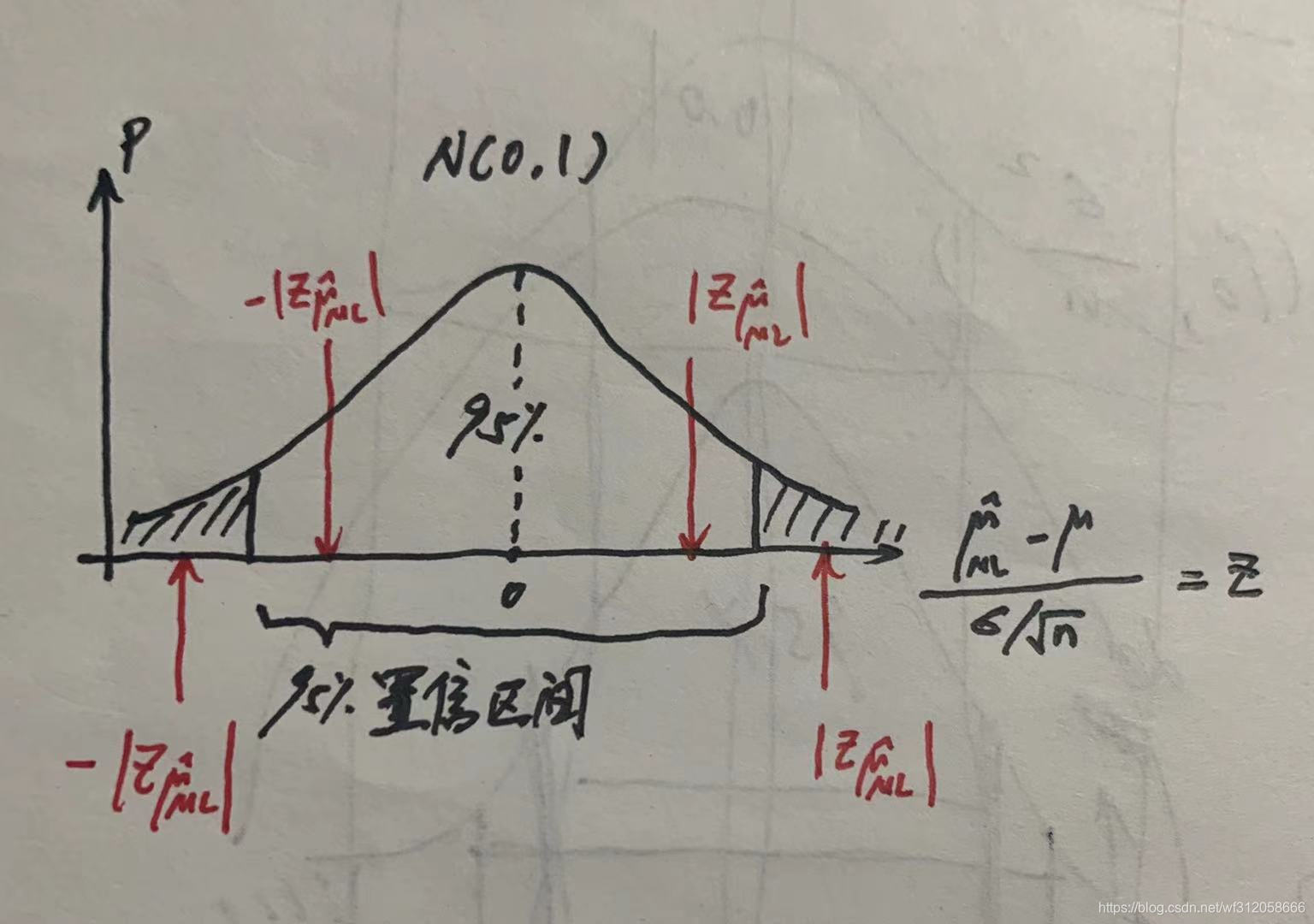
该上图标准正态分布两边阴影面积的概率为1-95%=5%=0.05，假设我们把0.05概率当成我们人类可以接受极端概率发生的总和。
那么如果$\pm |z_{{\bar{\mu }}_{ML}}|$在95%区间内，它的p值= 2 P { Z < − ∣ z μ ˉ M L ∣ } 2P\{Z<-|z_{\bar \mu_{ML}}|\} 2P{Z<−∣zμˉ​ML​​∣}>0.05,所以，原假设$\mu ={\mu }_0$我们认为可以发生，即使${\bar{\mu }}_{ML}$和${\mu }_0$差了十万八千里，就像我们举过的例子，真参平均身高1.7米，你猜1.65.但你抽的样本很背，抽到样本均值身高2米，但你利用p值发现你的原假设其实是对的。因为原假设的概率 P { ± z μ ˉ M L } P\{±z_{\bar \mu_{ML}}\} P{±zμˉ​ML​​}在很多极端事情的里面，而这个这些极端事情发生的概率我们认为是可接受的，即可发生的.

那么如果$\pm |z_{{\bar{\mu }}_{ML}}|$在95%区间外，它的p值= 2 P { Z < − ∣ z μ ˉ M L ∣ } 2P\{Z<-|z_{\bar \mu_{ML}}|\} 2P{Z<−∣zμˉ​ML​​∣}<0.05,这概率就低于我们认可的极端概率发生的总和。那么它是真的太难发生了。所以原假设$\mu ={\mu }_0$我们认为太难发生了，也就是错的.千万别钻牛角尖，有的同学会说，在难也会发生，是没错，人嘛抱有希望是对的，但普罗大众认为不可能，认为不可能发生。

现在我们来学学几句官话：
p-值的具体评级(grade of p-value):

p>0.05,我们的样本数据有很弱的证据(weak evidence)来违抗我们的原假设.(原假设正确）

0.01<p<0.05,我们的样本数据有着适当的证据(moderate evidence)来违抗我们的原假设。(原假设还行吧，不好不坏)

p<0.01,我们的样本数据有很强的证据(strong evidence)来违抗我们的原假设.(原假设错误）

好到这，我相信大家对p值和假设检验有了最基本的了解，系好安全带，我们才刚刚开始，现在准备起飞。

检验正态分布的均值，已知方差(Test mean of normal distribution with known variance)
1.原假设$H_0:\mu ={\mu }_0$,备择假设$H_1:\mu \ne {\mu }_0$:
那么:
$$Z=({\bar{\mu }}_{ML}-\mu )/(\sigma \sqrt{n})～N(0,1)$$
保留该标准正态分布的左侧和右侧阈值。

再计算z-score：
$$z_{{\bar{\mu }}_{ML}}=({\bar{\mu }}_{ML}-{\mu }_0)/(\sigma \sqrt{n})～N(0,1)$$

计算p-值:
p = 1 − P ( − ∣ z μ ˉ M L ∣ < Z < + ∣ z μ ˉ M L ∣ ) = 2 P { Z < − ∣ z μ ˉ M L ∣ } p=1-P(-|z_{\bar \mu_{ML}}|<Z<+|z_{\bar \mu_{ML}}|)=2P\{Z<-|z_{\bar \mu_{ML}}|\} p=1−P(−∣zμˉ​ML​​∣<Z<+∣zμˉ​ML​​∣)=2P{Z<−∣zμˉ​ML​​∣}
那么综合上述，如下图(双边检验):

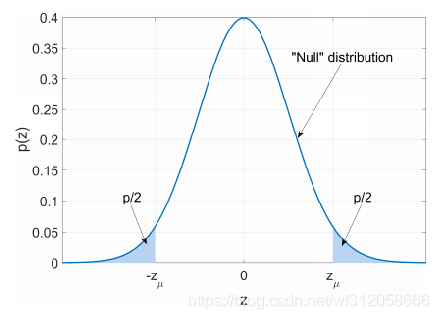
图中的Null 为原假设，$\pm z_{\mu }$为$\pm z_{{\bar{\mu }}_{ML}}$, z为$Z$, p为p值。我们再根据p值的评级来判断是否原假设成立或不成立.

原假设是"="，对立假设是"≠"。那么我们根据对立假设"≠"，而不是原假设是"="。因为"≠"，所以在$Z=({\bar{\mu }}_{ML}-\mu )/(\sigma \sqrt{n})～N(0,1)$中，为这个标准正态分布的两小端即左和右阈值的左端和右端，所以$z_{{\bar{\mu }}_{ML}}$这个公式要考虑我们要考虑正方向和反方向即$\pm |z_{{\bar{\mu }}_{ML}}|$,所以也被称为双边检验(both side test)。

2.原假设$H_0:\mu <={\mu }_0$,备择假设$H_1:\mu >{\mu }_0$:
其实我们也能写成原假设$H_0:\mu ={\mu }_0$,备择假设$H_1:\mu >{\mu }_0$。

但没有原假设$H_0:\mu <{\mu }_0$,备择假设$H_1:\mu >{\mu }_0$这写法，切记，为什么?

我们还是先看当原假设$H_0:\mu ={\mu }_0$,备择假设$H_1:\mu \ne {\mu }_0$我们知道这是两边检验p值。如果p值过大，则$H_0:\mu ={\mu }_0$成立。

当原假设不变，备择假设为$H_1:\mu >{\mu }_0$时，我们自然是去左边阈值留右边阈值，因为我们基于备择假设要算极端事件概率如下图（单边检验）:

当p值再大一些超过阈值时，是不是已经进入$\mu ={\mu }_0$的范畴内了，但我们也清晰的看到，除了中间侧一大段，也囊括了左侧一小段即$\mu <{\mu }_0$而这一小段的概率是极低的，即阈值，如下图:

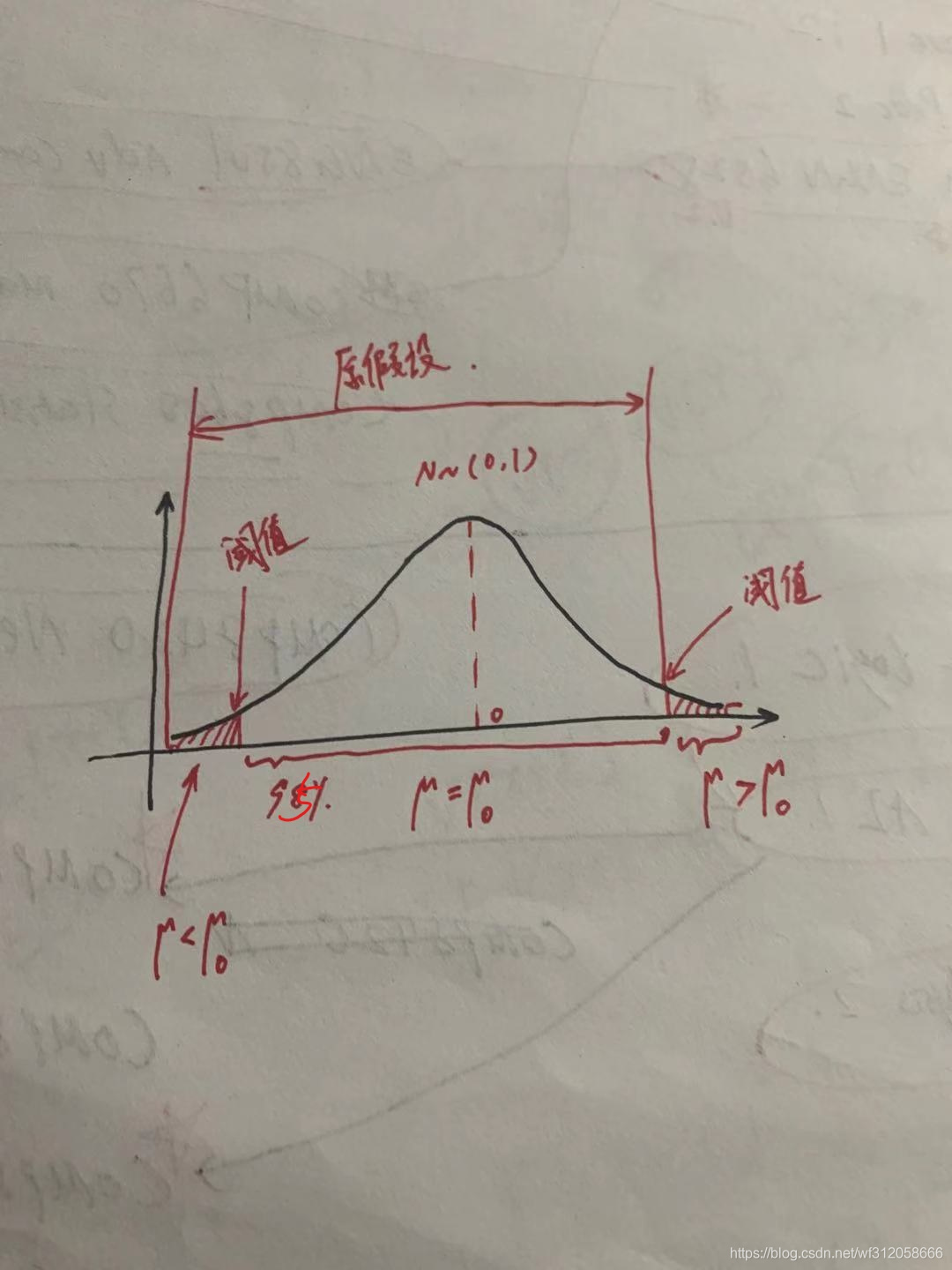
正如上图所示，其实大部分95%概率均支持原假设$\mu ={\mu }_0$，但一小部分概率支持即2.5%支持原假设$\mu <{\mu }_0$,所以我们可以写成原假设$H_0：\mu ={\mu }_0$或者$H_0：\mu <={\mu }_0$,但不能写成$H_0：\mu <{\mu }_0$因为对比$\mu ={\mu }_0$的概率它的概率太小了。所以在$H_0：\mu <={\mu }_0$中，其实重点是$\mu ={\mu }_0$.

言归正传，在算法方面还是大同小异:

$$Z=({\bar{\mu }}_{ML}-\mu )/(\sigma \sqrt{n})～N(0,1)$$
保留该标准正态分布的右侧阈值。

再计算z-score:
$$z_{{\bar{\mu }}_{ML}}=({\bar{\mu }}_{ML}-{\mu }_0)/(\sigma \sqrt{n})～N(0,1)$$

然后计算p值:
p = P { Z > z μ ˉ M L } = 1 − P { Z < z μ ˉ M L } p=P\{Z>z_{\bar \mu_{ML}}\}=1-P\{Z<z_{\bar \mu_{ML}}\} p=P{Z>zμˉ​ML​​}=1−P{Z<zμˉ​ML​​}

我们再根据p值的评级来判断是否原假设成立或不成立.
这种检验也被称为单边检验(one-side test)

3.原假设$H_0:\mu >={\mu }_0$,备择假设$H_1:\mu <{\mu }_0$:
根据上述2所写，同理，我们也能写成原假设$H_0:\mu ={\mu }_0$。
$$Z=({\bar{\mu }}_{ML}-\mu )/(\sigma \sqrt{n})～N(0,1)$$
保留该标准正态分布的左侧阈值。
再计算:
$$z_{{\bar{\mu }}_{ML}}=({\bar{\mu }}_{ML}-{\mu }_0)/(\sigma \sqrt{n})～N(0,1)$$

然后计算p值:
p = P { Z < z μ ˉ M L } p=P\{Z<z_{\bar \mu_{ML}}\} p=P{Z<zμˉ​ML​​}
我们再根据p值的评级来判断是否原假设成立或不成立.
这种检验也被称为单边检验。

检验正态分布的均值，已知方差(Test mean of normal distribution with known variance)小结

原假设(H0)	备择假设(H1)	测试统计数据(Test statistic,z score)	p值	阈值
$\mu ={\mu }_0$	$\mu \ne {\mu }_0$	$z_{{\bar{\mu }}_{ML}}=({\bar{\mu }}_{ML}-{\mu }_0)/(\sigma \sqrt{n})$	2 P { Z < − 2P\{Z<- 2P{Z<−I$z_{{\bar{\mu }}_{ML}}$ I$\}$	保留两端
$\mu <={\mu }_0$	$\mu >{\mu }_0$	$z_{{\bar{\mu }}_{ML}}=({\bar{\mu }}_{ML}-{\mu }_0)/(\sigma \sqrt{n})$	1 − P { Z < z μ ˉ M L } 1-P\{Z<z_{\bar \mu_{ML}}\} 1−P{Z<zμˉ​ML​​}	保留右端
$\mu >={\mu }_0$	$\mu <{\mu }_0$	$z_{{\bar{\mu }}_{ML}}=({\bar{\mu }}_{ML}-{\mu }_0)/(\sigma \sqrt{n})$	P { Z < z μ ˉ M L } P\{Z<z_{\bar \mu_{ML}}\} P{Z<zμˉ​ML​​}	保留左端

*$Z～N(0,1)$

看到这里，大家基本上对假设检验和p值得原理有了充足的认识，那么我们就可以结合第4章，根据它们不同的分布，来判断图像，找阈值，算p值，判断原假设是否成立，均大同小异。

检验正态分布的均值，未知方差(Test mean of normal distribution with unknown variance)（t检验，t-test）
(具体分布原理请看第4章:置信区间与样本均值和总体方差）

无偏差估计计算均值：
$${\bar{\mu }}_{ML}=\bar{Y}=\frac{1}{n}\sum _{i=1}^n{Y}_i～N(\mu ,\frac{{\sigma }^2}{n})$$

无偏差估计计算方差：
$${\bar{\sigma }}^2=\frac{1}{n-1}\sum _{i=1}^n(y_i-{\bar{\mu }}_{ML}{)}^2$$

计算测试统计数据(Test statistic,t score) t-score:
$$t_{{\bar{\mu }}_{ML}}=({\bar{\mu }}_{ML}-{\mu }_0)/(\bar{\sigma }\sqrt{n})～T(n-1)$$
我们知道，它服从n-1自由度的t-分布。所以也叫t检测(t-test)
之后一样的操作，计算p值，评价p值，判断原假设是否成立.

原假设(H0)	备择假设(H1)	测试统计数据(Test statistic,t score)	p值	阈值
$\mu ={\mu }_0$	$\mu \ne {\mu }_0$	$({\bar{\mu }}_{ML}-{\mu }_0)/(\bar{\sigma }\sqrt{n})$	2 P { T < − 2P\{T<- 2P{T<−I$t_{{\bar{\mu }}_{ML}}$ I$\}$	保留两端
$\mu <={\mu }_0$	$\mu >{\mu }_0$	$({\bar{\mu }}_{ML}-{\mu }_0)/(\bar{\sigma }\sqrt{n})$	1 − P { T < t μ ˉ M L } 1-P\{T<t_{\bar \mu_{ML}}\} 1−P{T<tμˉ​ML​​}	保留右端
$\mu >={\mu }_0$	$\mu <{\mu }_0$	$({\bar{\mu }}_{ML}-{\mu }_0)/(\bar{\sigma }\sqrt{n})$	P { T < t μ ˉ M L } P\{T<t_{\bar \mu_{ML}}\} P{T<tμˉ​ML​​}	保留左端

*$T～T(n-1)$

检验不同正态分布的均值是否相同，已知方差(Test difference mean of normal distribution with known variance)
(具体分布原理请看第4章:置信区间和样本均值的差值1.总体均值${\mu }_A$,${\mu }_B$未知，总体方差${\sigma }_A^2$，${\sigma }_B^2$已知）

分别计算对应的无偏估计均值:
$${\bar{\mu }}_x=\frac{1}{n_x}\sum _{i=1}^{n_x}{x}_i,{\bar{\mu }}_y=\frac{1}{n_y}\sum _{i=1}^{n_y}{y}_i$$

假如原假设成立则${\mu }_x-{\mu }_y=0$，所以：
$${\bar{\mu }}_x-{\bar{\mu }}_y～N({\mu }_x-{\mu }_y=0,\frac{{\sigma }_x^2}{n_x}+\frac{{\sigma }_y^2}{n_y})$$

则z-score：
$$z_{({\bar{\mu }}_x-{\bar{\mu }}_y)}=({\bar{\mu }}_x-{\bar{\mu }}_y)/\sqrt{\frac{{\sigma }_x^2}{n_x}+\frac{{\sigma }_y^2}{n_y}}～N(0,1)$$

原假设(H0)	备择假设(H1)	测试统计数据(Test statistic,z score)	p值	阈值
${\mu }_x={\mu }_y$	${\mu }_x\ne {\mu }_y$	$z_{({\bar{\mu }}_x-{\bar{\mu }}_y)}=({\bar{\mu }}_x-{\bar{\mu }}_y)/\sqrt{\frac{{\sigma }_x^2}{n_x}+\frac{{\sigma }_y^2}{n_y}}$	2 P { Z < − 2P\{Z<- 2P{Z<−I$z_{({\bar{\mu }}_x-{\bar{\mu }}_y)}$ I$\}$	保留两端
${\mu }_x<={\mu }_y$	${\mu }_x>{\mu }_y$	$z_{({\bar{\mu }}_x-{\bar{\mu }}_y)}=({\bar{\mu }}_x-{\bar{\mu }}_y)/\sqrt{\frac{{\sigma }_x^2}{n_x}+\frac{{\sigma }_y^2}{n_y}}$	1 − P { Z < z ( μ ˉ x − μ ˉ y ) } 1-P\{Z<z_{(\bar\mu_x-\bar\mu_y)}\} 1−P{Z<z(μˉ​x​−μˉ​y​)​}	保留右端
${\mu }_x>={\mu }_y$	${\mu }_x<{\mu }_y$	$z_{({\bar{\mu }}_x-{\bar{\mu }}_y)}=({\bar{\mu }}_x-{\bar{\mu }}_y)/\sqrt{\frac{{\sigma }_x^2}{n_x}+\frac{{\sigma }_y^2}{n_y}}$	P { Z < z ( μ ˉ x − μ ˉ y ) } P\{Z<z_{(\bar\mu_x-\bar\mu_y)}\} P{Z<z(μˉ​x​−μˉ​y​)​}	保留左端

*$Z～N(0,1)$

检验不同正态分布的均值是否相同，未知方差(Test difference mean of normal distribution with known variance)
(具体分布原理请看第4章:置信区间和样本均值的差值2.总体均值${\mu }_A$,${\mu }_B$未知，总体方差${\sigma }_A^2$，${\sigma }_B^2$未知.）

分别计算对应的无偏估计均值:
$${\bar{\mu }}_x=\frac{1}{n_x}\sum _{i=1}^{n_x}{x}_i,{\bar{\mu }}_y=\frac{1}{n_y}\sum _{i=1}^{n_y}{y}_i$$
分别计算对应的无偏估计方差:
$${\bar{\sigma }}_x^2=\frac{1}{n_x-1}\sum _{i=1}^{n_x}(x_i-{\bar{\mu }}_x{)}^2,{\bar{\sigma }}_y^2=\frac{1}{n_y-1}\sum _{i=1}^{n_y}(y_i-{\bar{\mu }}_y{)}^2$$
情况1.未知方差相同
假如原假设成立则${\mu }_x-{\mu }_y=0$，所以：
$$\frac{{\bar{\mu }}_x-{\bar{\mu }}_y}{\sqrt{\frac{{\sigma }^2}{n_x}+\frac{{\sigma }^2}{n_y}}}～N(0,1)$$
t-score:
$$t_{({\bar{\mu }}_x-{\bar{\mu }}_y)}=\frac{{\bar{\mu }}_x-{\bar{\mu }}_y}{\sqrt{\frac{{\sigma }^2}{n_x}+\frac{{\sigma }^2}{n_y}}}/\sqrt{\frac{{\chi }_{n_x+n_y-2}^2}{n_x+n_y-2}}～T(n_x+n_y-2)$$
我们令:
$$S_p^2=\frac{(n_x-1){\bar{\sigma }}_x^2+(n_y-1){\bar{\sigma }}_y^2}{(n_x+n_y-2)}$$
则:
$$t_{({\bar{\mu }}_x-{\bar{\mu }}_y)}=({\bar{\mu }}_x-{\bar{\mu }}_y)/\sqrt{S_p^2(\frac{1}{n_x}+\frac{1}{n_y})}～T(n_x+n_y-2)$$

原假设(H0)	备择假设(H1)	测试统计数据(Test statistic,t score)	p值	阈值
${\mu }_x={\mu }_y$	${\mu }_x\ne {\mu }_y$	$({\bar{\mu }}_x-{\bar{\mu }}_y)/\sqrt{S_p^2(\frac{1}{n_x}+\frac{1}{n_y})}$	2 P { T < − 2P\{T<- 2P{T<−I$t_{({\bar{\mu }}_x-{\bar{\mu }}_y)}$ I$\}$	保留两端
${\mu }_x<={\mu }_y$	${\mu }_x>{\mu }_y$	$({\bar{\mu }}_x-{\bar{\mu }}_y)/\sqrt{S_p^2(\frac{1}{n_x}+\frac{1}{n_y})}$	1 − P { T < t ( μ ˉ x − μ ˉ y ) } 1-P\{T<t_{(\bar\mu_x-\bar\mu_y)}\} 1−P{T<t(μˉ​x​−μˉ​y​)​}	保留右端
${\mu }_x>={\mu }_y$	${\mu }_x<{\mu }_y$	$({\bar{\mu }}_x-{\bar{\mu }}_y)/\sqrt{S_p^2(\frac{1}{n_x}+\frac{1}{n_y})}$	P { T < t ( μ ˉ x − μ ˉ y ) } P\{T<t_{(\bar\mu_x-\bar\mu_y)}\} P{T<t(μˉ​x​−μˉ​y​)​}	保留左端

*$T～T(n_x+n_y-2)$

情况2.未知方差不同:

假如原假设成立则${\mu }_x-{\mu }_y=0$，
$${\bar{\mu }}_x-{\bar{\mu }}_y～N({\mu }_x-{\mu }_y=0,\frac{{\bar{\sigma }}_x^2}{n_x}+\frac{{\bar{\sigma }}_y^2}{n_y})$$
z-score:
$$({\bar{\mu }}_x-{\bar{\mu }}_y)/\sqrt{\frac{{\bar{\sigma }}_x^2}{n_x}+\frac{{\bar{\sigma }}_y^2}{n_y}}～N(0,1)$$

原假设(H0)	备择假设(H1)	测试统计数据(Test statistic,z score)	p值	阈值
${\mu }_x={\mu }_y$	${\mu }_x\ne {\mu }_y$	$({\bar{\mu }}_x-{\bar{\mu }}_y)/\sqrt{\frac{{\bar{\sigma }}_x^2}{n_x}+\frac{{\bar{\sigma }}_y^2}{n_y}}$	2 P { Z < − 2P\{Z<- 2P{Z<−I$z_{({\bar{\mu }}_x-{\bar{\mu }}_y)}$ I$\}$	保留两端
${\mu }_x<={\mu }_y$	${\mu }_x>{\mu }_y$	$({\bar{\mu }}_x-{\bar{\mu }}_y)/\sqrt{\frac{{\bar{\sigma }}_x^2}{n_x}+\frac{{\bar{\sigma }}_y^2}{n_y}}$	1 − P { Z < z ( μ ˉ x − μ ˉ y ) } 1-P\{Z<z_{(\bar\mu_x-\bar\mu_y)}\} 1−P{Z<z(μˉ​x​−μˉ​y​)​}	保留右端
${\mu }_x>={\mu }_y$	${\mu }_x<{\mu }_y$	$({\bar{\mu }}_x-{\bar{\mu }}_y)/\sqrt{\frac{{\bar{\sigma }}_x^2}{n_x}+\frac{{\bar{\sigma }}_y^2}{n_y}}$	P { Z < z ( μ ˉ x − μ ˉ y ) } P\{Z<z_{(\bar\mu_x-\bar\mu_y)}\} P{Z<z(μˉ​x​−μˉ​y​)​}	保留左端

*$Z～N(0,1)$

检验方差(test variance),方差，均值都未知
(具体分布原理请看第4章:置信区间和样本均值的差值2.总体均值${\mu }_A$,${\mu }_B$未知，总体方差${\sigma }_A^2$，${\sigma }_B^2$未知.）

$$\frac{{\sum }_{i=1}^n(y_i-\bar{y}{)}^2}{{\sigma }^2}=\frac{(n-1)S^2}{{\sigma }^2}～{\chi }^2(n-1)$$
$S^2$为样本方差.

如果原假设正确，则${\sigma }^2={\sigma }_0^2$:
$$\frac{{\sum }_{i=1}^n(y_i-\bar{y}{)}^2}{{\sigma }_0^2}=\frac{(n-1)S^2}{{\sigma }_0^2}～{\chi }^2(n-1)$$
据小弟所知，好像这个验测统计数据没有名字，不像前面的官方叫z-score或者t-score，但小弟上学期间，老师喜欢叫它为c，并且因为它的分布服从n-1 自由度的卡方(chi-square)英语开头有个c，那么我们就叫它c-score吧。即$c=\frac{(n-1)S^2}{{\sigma }_0^2}$
但不巧的是卡方分布跟正态分布不太一样，它是x轴上才会有概率分布，并且它也不基于x轴上某点对称。那么如果原假设为${\sigma }^2={\sigma }_0^2$,我们算的c-score可能会导致一边在阈值以外，一边在阈值以内这种情况依旧拒绝原假设，所以我们要取最小的一端乘2作为p值，即:
p v a l u e = 2 m i n ( P { χ n − 1 2 < c } , 1 − P {   χ n − 1 2 < c } ) p_{value}=2min(P\{\chi^2_{n-1}<c\},1-P\{\ \chi^2_{n-1}<c\}) pvalue​=2min(P{χn−12​<c},1−P{ χn−12​<c})

原假设(H0)	备择假设(H1)	测试统计数据(Test statistic,c score)	p值	阈值
${\sigma }^2={\sigma }_0^2$	${\sigma }^2\ne {\sigma }_0^2$	$\frac{(n-1)S^2}{{\sigma }_0^2}$	2 m i n ( P { χ n − 1 2 < c } , 1 − P {   χ n − 1 2 < c } ) 2min(P\{\chi^2_{n-1}<c\},1-P\{\ \chi^2_{n-1}<c\}) 2min(P{χn−12​<c},1−P{ χn−12​<c})	保留两端
${\sigma }^2<={\sigma }_0^2$	${\sigma }^2>{\sigma }_0^2$	$\frac{(n-1)S^2}{{\sigma }_0^2}$	1 − P { χ n − 1 2 < c } 1-P\{\chi^2_{n-1}<c\} 1−P{χn−12​<c}	保留右端
${\sigma }^2>={\sigma }_0^2$	${\sigma }^2<{\sigma }_0^2$	$\frac{(n-1)S^2}{{\sigma }_0^2}$	P { χ n − 1 2 < c } P\{\chi^2_{n-1}<c\} P{χn−12​<c}	保留左端

*$c～{\chi }^2(n-1)$

检验不同方差(test for different variance):
(具体分布原理请看第4章:置信区间估计方差的比,方差未知，均值未知.）
分别计算样本方差:
$$S_x^2=\frac{{\sum }_{i=1}^n(x_i-{\bar{\mu }}_x{)}^2}{n},S_y^2=\frac{{\sum }_{i=1}^m(y_i-{\bar{\mu }}_y{)}^2}{m}$$
如果原假设正确，则${\sigma }_x^2={\sigma }_y^2$:
$$\frac{S_x^2}{S_y^2}～F(n-1,m-1)$$

据小弟所知，好像这个验测统计数据没有名字，不像前面的官方叫z-score或者t-score，我们叫它f-score吧。

f分布计算p值同理于卡方分布的p值计算,若原假设${\sigma }_x^2={\sigma }_y^2$,那么p值为:
p = 2 m i n ( P { F n − 1 , m − 1 < f } , 1 − P { F n − 1 , m − 1 < f } ) p=2min(P\{F_{n-1,m-1}<f\},1-P\{F_{n-1,m-1}<f\}) p=2min(P{Fn−1,m−1​<f},1−P{Fn−1,m−1​<f})

原假设(H0)	备择假设(H1)	测试统计数据(Test statistic,f score)	p值	阈值
${\sigma }_x^2={\sigma }_y^2$	${\sigma }_x^2\ne {\sigma }_y^2$	$\frac{S_x^2}{S_y^2}$	p = 2 m i n ( P { F n − 1 , m − 1 < f } , 1 − P { F n − 1 , m − 1 < f } ) p=2min(P\{F_{n-1,m-1}<f\},1-P\{F_{n-1,m-1}<f\}) p=2min(P{Fn−1,m−1​<f},1−P{Fn−1,m−1​<f})	保留两端
${\sigma }_x^2<={\sigma }_y^2$	${\sigma }_x^2>{\sigma }_y^2$	$\frac{S_x^2}{S_y^2}$	1 − P { F n − 1 , m − 1 < f } ) 1-P\{F_{n-1,m-1}<f\}) 1−P{Fn−1,m−1​<f})	保留右端
${\sigma }_x^2>={\sigma }_y^2$	${\sigma }_x^2<{\sigma }_y^2$	$\frac{S_x^2}{S_y^2}$	P { F n − 1 , m − 1 < f } P\{F_{n-1,m-1}<f\} P{Fn−1,m−1​<f}	保留左端

*$f～F(n-1,m-1)$

检验二项式分布真参数$\theta$
(具体分布原理请看第4章:置信区间估计均值(期望)例题2)
我们回顾下
计算无偏估计$\theta$,似然估计，详请看第三章似然无偏估计二项式分布参数$\theta$
$$\bar{\theta }=\frac{1}{n}\sum _{i=1}^n{y}_i=\frac{m}{n}$$
因为y成功为1，失败为0，m即为总的成功数目.
n为实验多少次.
当n→∞时，利用中心极限定理并且如果我们的原假设$\theta ={\theta }_0$正确，则:
$$\bar{\theta }{\to }^{d}N({\theta }_0,\frac{{\theta }_0(1-{\theta }_0)}{n})$$

那么,z-score为:
$$(\bar{\theta }-{\theta }_0)/\sqrt{\frac{{\theta }_0(1-{\theta }_0)}{n}}{\to }^{d}N(0,1)$$

原假设(H0)	备择假设(H1)	测试统计数据(Test statistic,z score)	p值	阈值
$\theta ={\theta }_0$	$\theta \ne {\theta }_0$	$(\bar{\theta }-{\theta }_0)/\sqrt{\frac{{\theta }_0(1-{\theta }_0)}{n}}$	2 P { Z < − 2P\{Z<- 2P{Z<−I$z$ I$\}$	保留两端
$\theta <={\theta }_0$	$\theta >{\theta }_0$	$(\bar{\theta }-{\theta }_0)/\sqrt{\frac{{\theta }_0(1-{\theta }_0)}{n}}$	1 − P { Z < z } 1-P\{Z<z\} 1−P{Z<z}	保留右端
$\theta >={\theta }_0$	$\theta <{\theta }_0$	$(\bar{\theta }-{\theta }_0)/\sqrt{\frac{{\theta }_0(1-{\theta }_0)}{n}}$	P { Z < z } P\{Z<z\} P{Z<z}	保留左端

*$Z～N(0,1)$

检验不同二项式分布参数差:
分别计算对应的无偏估计$\theta$当n→∞时，利用中心极限定理：
$${\bar{\theta }}_x=\frac{1}{n_x}\sum _{i=1}^{n_x}{y}_i=\frac{m_x}{n_x}{\to }^{d}N({\theta }_x,\frac{{\theta }_x(1-{\theta }_x)}{n_x})$$
$${\bar{\theta }}_y=\frac{1}{n_y}\sum _{i=1}^{n_y}{y}_i=\frac{m_y}{n_y}{\to }^{d}N({\theta }_y,\frac{{\theta }_y(1-{\theta }_y)}{n_y})$$
那么:
$${\bar{\theta }}_x-{\bar{\theta }}_y{\to }^{d}N({\theta }_x-{\theta }_y,\frac{{\theta }_x(1-{\theta }_x)}{n_x}+\frac{{\theta }_y(1-{\theta }_y)}{n_y})$$
上述公式利用了E[X-Y]=E[X]-E[Y], V[X-Y]=V[X]+V[Y]，详推导请看第二章方差和期望.

又因为我们假设原假设${\theta }_x={\theta }_y=\theta$成立:
那我们可以无偏估计$\theta$,即:
$${\theta }_y={\theta }_x={\bar{\theta }}_p=\frac{m_x+m_y}{n_x+n_y}$$
$m_x$和$m_y$为对应$n_x$和$n_y$个事件里成功多少次
得:
$${\bar{\theta }}_x-{\bar{\theta }}_y{\to }^{d}N({\theta }_x-{\theta }_y=0,{\bar{\theta }}_p(1-{\bar{\theta }}_p)(\frac{1}{n_x}+\frac{1}{n_y}))$$

那么我们的z-score，为:
$$z=({\bar{\theta }}_x-{\bar{\theta }}_y)/\sqrt{{\bar{\theta }}_p(1-{\bar{\theta }}_p)(\frac{1}{n_x}+\frac{1}{n_y})}～N(0,1)$$

原假设(H0)	备择假设(H1)	测试统计数据(Test statistic,z score)	p值	阈值
${\theta }_x={\theta }_y$	${\theta }_x\ne {\theta }_y$	$({\bar{\theta }}_x-{\bar{\theta }}_y)/\sqrt{{\bar{\theta }}_p(1-{\bar{\theta }}_p)(\frac{1}{n_x}+\frac{1}{n_y})}$	2 P { Z < − 2P\{Z<- 2P{Z<−I$z$ I$\}$	保留两端
${\theta }_x<={\theta }_y$	${\theta }_x>{\theta }_y$	$({\bar{\theta }}_x-{\bar{\theta }}_y)/\sqrt{{\bar{\theta }}_p(1-{\bar{\theta }}_p)(\frac{1}{n_x}+\frac{1}{n_y})}$	1 − P { Z < z } 1-P\{Z<z\} 1−P{Z<z}	保留右端
${\theta }_x>={\theta }_y$	${\theta }_x<{\theta }_y$	$({\bar{\theta }}_x-{\bar{\theta }}_y)/\sqrt{{\bar{\theta }}_p(1-{\bar{\theta }}_p)(\frac{1}{n_x}+\frac{1}{n_y})}$	P { Z < z } P\{Z<z\} P{Z<z}	保留左端

*$Z～N(0,1)$

测验泊松分布参数$\lambda$
泊松分布的参数检验很有意思，小弟当时认为可以用检验正态分布均值，已知方差的想法来测验泊松参数，但失败了，等老师讲的时候，你才会发现，不用那么费劲很简单，利用泊松分布的含义即可.

如果我们观测的数据是X=x,在一段时间内发生x个事件，那么我们假设原假设成立，即$\lambda ={\lambda }_0$,那基于周期发生${\lambda }_0$的情况下，我们观测我们的事件x个
观测比它多的情况，和少的情况对应累计的概率作为极端概率和(p值)，再看是否超过我们的阈值即可:
P λ 0 { X > = x } < = α / 2 , P λ 0 { X < = x } < = α / 2 P_{\lambda_0}\{X>=x\}<=\alpha/2, P_{\lambda_0}\{X<=x\}<=\alpha/2 Pλ0​​{X>=x}<=α/2,Pλ0​​{X<=x}<=α/2
$P_{{\lambda }_0}$为基于周期为${\lambda }_0$的泊松分布概率.

那么p值为:
p = 2 m i n ( P λ 0 { X > = x } , P λ 0 { X < = x } ) p=2min(P_{\lambda_0}\{X>=x\},P_{\lambda_0}\{X<=x\}) p=2min(Pλ0​​{X>=x},Pλ0​​{X<=x})

原假设(H0)	备择假设(H1)	测试统计数据(Test statistic)	p值	阈值
$\lambda ={\lambda }_0$	$\lambda \ne {\lambda }_0$	$x$	2 m i n ( P λ 0 { X > = x } , P λ 0 { X < = x } ) 2min(P_{\lambda_0}\{X>=x\},P_{\lambda_0}\{X<=x\}) 2min(Pλ0​​{X>=x},Pλ0​​{X<=x})	保留两端
$\lambda <={\lambda }_0$	$\lambda >{\lambda }_0$	$x$	P λ 0 { X > = x } P_{\lambda_0}\{X>=x\} Pλ0​​{X>=x}	保留右端
$\lambda >={\lambda }_0$	$\lambda <{\lambda }_0$	$x$	P λ 0 { X < = x } P_{\lambda_0}\{X<=x\} Pλ0​​{X<=x}	保留左端

*$X～Poi({\lambda }_0)$

测验不同泊松分布参数$\lambda$的关系
这里有$X_1～Poi({\lambda }_1)$和$X_2～Poi({\lambda }_2)$,${\lambda }_1,{\lambda }_2$未知
现在我们要测验:
$$H_0:{\lambda }_2=c{\lambda }_1$$
$$H_1:{\lambda }_2\ne c{\lambda }_1$$
c是你猜的数值

我们把$X_1$个事件当成成功，$X_2$个事件当成失败，那对应它们的泊松分布，那会有对应的概率.如果${\lambda }_1$和${\lambda }_2$真有c倍的关系的话，那$X_1$个事件和$X_2$个事件肯定有对应的变化.

那么我们利用条件概率:
P { X 1 = k ∣ X 1 + X 2 = n } P\{X_1=k|X_1+X_2=n \} P{X1​=k∣X1​+X2​=n}
意味着,在所有事件中，发生$X_1$个事件的概率是多少.

化简该公式:
P { X 1 = k ∣ X 1 + X 2 = n } = P { X 1 = k ， X 1 + X 2 = n } P { X 1 + X 2 = n } = P { X 1 = k , X 2 = n − k } P { X 1 + X 2 = n } = P { X 1 = k } P { X 2 = n − k } P { X 1 + X 2 = n } P\{X_1=k|X_1+X_2=n \}=\frac{P\{X_1=k，X_1+X_2=n\}}{P\{X_1+X_2=n\}}=\frac{P\{X_1=k,X_2=n-k\}}{P\{X_1+X_2=n\}}=\frac{P\{X_1=k\}P\{X_2=n-k\}}{P\{X_1+X_2=n\}} P{X1​=k∣X1​+X2​=n}=P{X1​+X2​=n}P{X1​=k，X1​+X2​=n}​=P{X1​+X2​=n}P{X1​=k,X2​=n−k}​=P{X1​+X2​=n}P{X1​=k}P{X2​=n−k}​

利用对应的泊松分布得到概率，代入:
P { X 1 = k } P { X 2 = n − k } P { X 1 + X 2 = n } = e x p { − λ 1 } λ 1 k k ! e x p { − λ 2 } λ 2 n − k ( n − k ) ! e x p { − ( λ 1 + λ 2 ) } ( λ 1 + λ 2 ) n n ! \frac{P\{X_1=k\}P\{X_2=n-k\}}{P\{X_1+X_2=n\}}=\frac{\frac{exp\{-\lambda_1\}\lambda^k_1}{k!} \frac{exp\{-\lambda_2\}\lambda^{n-k}_2}{(n-k)!}}{\frac{exp\{-(\lambda_1+\lambda_2)\}(\lambda_1+\lambda_2)^n}{n!}} P{X1​+X2​=n}P{X1​=k}P{X2​=n−k}​=n!exp{−(λ1​+λ2​)}(λ1​+λ2​)n​k!exp{−λ1​}λ1k​​(n−k)!exp{−λ2​}λ2n−k​​​
上述公式分母用到了泊松分布的连加性，详看第二章概率分布。

我们接着整理上述公式:
e x p { − λ 1 } λ 1 k k ! e x p { − λ 2 } λ 2 n − k ( n − k ) ! e x p { − ( λ 1 + λ 2 ) } ( λ 1 + λ 2 ) n n ! = n ! ( n − k ) ! k ! ( λ 1 λ 1 + λ 2 ) k ( λ 2 λ 2 + λ 1 ) n − k \frac{\frac{exp\{-\lambda_1\}\lambda^k_1}{k!} \frac{exp\{-\lambda_2\}\lambda^{n-k}_2}{(n-k)!}}{\frac{exp\{-(\lambda_1+\lambda_2)\}(\lambda_1+\lambda_2)^n}{n!}}=\frac{n!}{(n-k)!k!}(\frac{\lambda_1}{\lambda_1+\lambda_2})^{k}(\frac{\lambda_2}{\lambda_2+\lambda_1})^{n-k} n!exp{−(λ1​+λ2​)}(λ1​+λ2​)n​k!exp{−λ1​}λ1k​​(n−k)!exp{−λ2​}λ2n−k​​​=(n−k)!k!n!​(λ1​+λ2​λ1​​)k(λ2​+λ1​λ2​​)n−k
看出来了么，上述公式这是什么，很明显的二项式分布.
如果原假设成立${\lambda }_2=c{\lambda }_1$，那么我们可以把${\lambda }_2$替换掉，得到:
$$Bin(\theta =\frac{1}{1+c},n)$$
即每件事成功概率为$\frac{1}{1+c}$，一共n个事件。
那么同理，在这个二项式分布中，如果假设成立${\lambda }_2=c{\lambda }_1$，那$X_1$个事件不能发生太多或太少，否则反对我们的原假设.

同理，我们知道二项式分布也不是对称的,那么p值为:
p = 2 m i n ( P B i n ( 1 1 + c , n ) { X > = x 1 } , P B i n ( 1 1 + c , n ) { X < = x 1 } ) p=2min(P_{Bin(\frac{1}{1+c},n)}\{X>=x_1\},P_{Bin(\frac{1}{1+c},n)}\{X<=x_1\}) p=2min(PBin(1+c1​,n)​{X>=x1​},PBin(1+c1​,n)​{X<=x1​})

原假设(H0)	备择假设(H1)	测试统计数据(Test statistic)	p值	阈值
${\lambda }_2=c{\lambda }_1$	${\lambda }_2\ne {\lambda }_1$	$x_1$	p = 2 m i n ( P B i n ( 1 1 + c , n ) { X > = x 1 } , P B i n ( 1 1 + c , n ) { X < = x 1 } ) p=2min(P_{Bin(\frac{1}{1+c},n)}\{X>=x_1\},P_{Bin(\frac{1}{1+c},n)}\{X<=x_1\}) p=2min(PBin(1+c1​,n)​{X>=x1​},PBin(1+c1​,n)​{X<=x1​})	保留两端
${\lambda }_2<=c{\lambda }_1$	${\lambda }_2>c{\lambda }_1$	$x_1$	P B i n ( 1 1 + c , n ) { X > = x 1 } P_{Bin(\frac{1}{1+c},n)}\{X>=x_1\} PBin(1+c1​,n)​{X>=x1​}	保留右端
${\lambda }_2>={\lambda }_1$	${\lambda }_2<c{\lambda }_1$	$x_1$	P B i n ( 1 1 + c , n ) { X < = x 1 } P_{Bin(\frac{1}{1+c},n)}\{X<=x_1\} PBin(1+c1​,n)​{X<=x1​}	保留左端

*$X～Bin(\frac{1}{1+c},n),X_1+X_2=n,X_1=x_1$

二.结语

辛苦各位看官和同学了，如有谬误请告知，小弟及时更改.
本章讲基本涵盖了我们通常会涉及到的所有情况，大部分题也是基于此更改，大家可以发现它们的共通点无疑两方面，找到涉及的分布，假设原假设成立。希望大家可以灵活运用，不仅明白原理加强数字的敏感度，更要明白它们背后的哲学想法，进而用理性和感性去学习，这样不仅可以帮助你做研究或项目皆易如反掌，更能在生活上为人做事也有独到的见解，做到爱自己，爱他人.
自习的同学请看Ross, S.M. (2014) Introduction to Probability and Statistics for Engineers and Scientists, 5th ed. Academic Press. 第8章