计算几何学习——点定位

目录

点定位问题

slab算法（基于简而治之的思想）

基于Kirkpatrick结构的方法（基于简而治之的思想）

梯形图

---

细分的图示，将一个区域进行划分：

点定位问题

定义：令是上有个顶点的细分，给定一个查询点，确定位于哪个面片中。

首先给出几个假设：

• 假设每个面片都标记为不同的数字

• S可以由合适的数据结构（eg.DCEL）表示

• 每个查询点部位与边或者顶点上

每个查询点部位与边或者顶点上

算法效率总结：

slab算法（基于简而治之的思想）

预处理：将细分沿竖直方向进行分割，每条分割线都经过一个顶点，每条分割线之间形成一个个slab。这些slab在下面的操作中会进行组织。

划分slab

不难发现，每个slab都含有很多梯形（三角形看做是退化的梯形），这些梯形在下面的操作中会进行排序组织。

进行数据组织：形成tree of trees

上面那棵树是对slab之间的数据组织，左边那棵树是对每个slab内部梯形的组织。

步骤：先x方向搜索，确定查询点位于哪个slab中，而后y方向搜索，确定查询点位于该slab的哪个梯形中。

基于Kirkpatrick结构的方法（基于简而治之的思想）

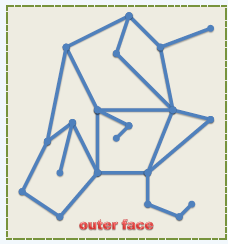
首先给出假设：假设所有面片都是三角形，而且out face也是三角形。如下图所示

构建层次结构：

于是产生了一个三角剖分序列,其中是最初始的三角剖分，是一个简单的三角形，也就是的out face。的每个三角形与有重叠的部分。

由产生：在中找到合适的顶点子集，移除这些顶点以及相应的边，对剩下的洞的部分重新三角剖分。

这里我们要找的顶点子集中的顶点需要是独立的，也就是每两个顶点不相邻，没有边连接这两个顶点。要求独立子集的规模达到原图的固定百分比（比如百分之五，百分之六等）即可。独立子集中的顶点个数越大越好，与的重叠部分越少越好。约定的每个三角形与中三角形重叠的个数不超过某一个常数，也就是控制每个被删除的顶点的度数即可。

独立子集构造算法：

由于平面图中度数不超过8的顶点数至少有个；一个一个检查n个顶点，当顶点的度数不少于8则忽略，否则将该顶点加入到独立子集中去，移除独立子集中该顶点的度数8的相邻点。

从而构成这样一个层次结构：

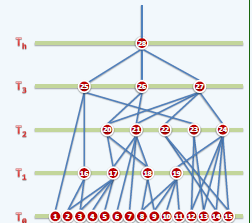
构造过程自底而上，查询过程自顶而下；这样的结构并不是一棵树，而是一个有向无环图（DAG）。

梯形图

考虑subdivision中的一条条不相冲突（除端点外不存在交点）线段

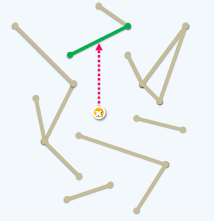
然后找到x的y方向上最上面的那条线段。

构建梯形图TM(S)

每个梯形都可以由top、bottom、left、right组成，left、right是由顶点所决定的。

Search Structure（SS）：DAG（有向无环图）

蓝色方块称为terminal Node，对应于每一个梯形，红色圆圈称为X-Node，对应为每一条线段的端点，橙色菱形称为Y-Node，对应于线段（非一一对应，可能一条线段对应多个Y-Node）

基于梯形图的构造方法:(基于随机递增思想)

首先用一个包围框R把所有的线段包含在其中，生成一个简单的梯形，也就是R（这里实际上是长方形）而后逐一将每条线段加入到梯形图中，使得梯形图进一步细化，而Search Structure得到拓展。

梯形细分可能的情况：

Case1：

Case2:

Case3:

下面给出一个例子：s、t是原有的线段，r是插入线段

插入线段的顺序是无关的，因此是随机算法，每次得到的SS是不同的，但是它的平均期望是很好的。