3-增量序列{3，2，1}的希尔排序时间复杂度分析

在本文中我们进行（3，2，1）-Shellsort在n元素随机序列的算法分析
1.pre
h = (h_t,h_t-1,…,h₂,h₁) : h₁=1的正整数向量
S₁(h;n): 第j趟排序进行的平均元素交换次数
I(L): L中含有的逆序数
L^(h,j): 长度为（n+h-1+j）/h的L的子序列（L[ j ],L[ j+h ],L[ j+2h ],…）
2.conclusion
for h = (3,2,1):
（1）S₁(h;n) = n²/12 +O(n);
（2）S₂(h;n) = （π/192）^1/2 * n^3/2 + O(n);
（3）S₃(h;n) = n/4 + O(n^2/3);
3.prove
(1) pass 1

如图，我们可以将L分成多行，每行代表一个子序列L^(3,j)（0 <= j < 3）
引用插入排序的结论，对一个随机序列，逆序数为n(n-1)/4
可得出
n_i = [(n+2-i)/3] (取下界)
容易算出 S₁(h;n) = n²/12 +O(n);
(2) pass 2
假设 n = 3m , m>0,经过pass1我们得到了一个3-order list
pass 2对L^(2,0) L^(2,1) 进行插入排序
S₂^(j) 表示L^(2,j) 中的逆序数，有
S₂（h;n）=S₂⁽⁰⁾ (n) +S₂⁽¹⁾ (n)
现在考虑一个L’ = {a₀,b₀,a₁,b₁,a₂,b₂……}
定义四个子序列
L_even,even = {a₀,b₀,a₂,b₂,a₄,b₄……}
L_even,odd = {a₀,b₁,a₂,b₃,a₄,b₅……}
L_odd,even = {b₀,a₁,b₂,a₃,b₄,a₅,……}
L_odd,odd = {a₁,b₁,a₃,b₃,a₅,b₅,……}
For each α，β ∈ {even, odd}, let X_α，β denote the random variable, defined on the set of L’, corresponding to the number of inversions in L, and let B_α，β (2m) = E(X_α，β ) for a random 2-ordered L’. Clearly,






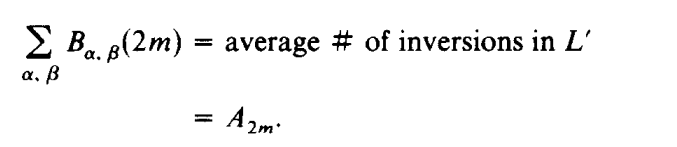
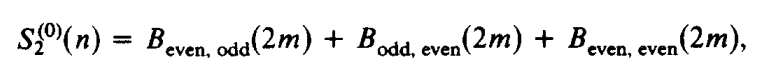
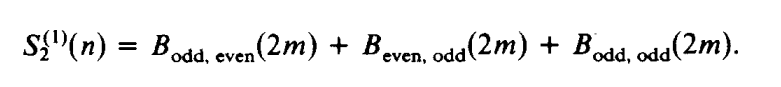
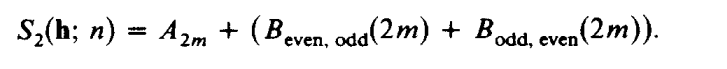
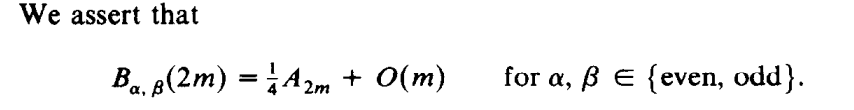
具体证明不加描述，想了解者可阅读文末参考文献
(2) pass 3
O(n^2/3) is an overestimate of the error term for S,.

An Analysis of (h, k, 1)-Shellsort*
ANDREW CHI-CHIH YAO
Conputer Science Deportment, Stanford CJniversi@, Stanford California 94305