二分图的最大匹配

whisperwdn

于 2021-12-17 23:45:30 发布

阅读量1.9k

点赞数 2

分类专栏：算法分析文章标签：算法数据结构

本文链接：https://blog.csdn.net/whisperwdn/article/details/121986144

版权

算法分析专栏收录该内容

6 篇文章 0 订阅

订阅专栏

本文介绍二分图最大匹配算法，有关离散数学中的简单知识不再赘述。如果觉得有用不要吝啬给博主点赞哦

一、定义

matching:
给定一个二分图G = (V,E)，M为E的子集，如果图中的顶点最多与M中的一条边相连，则称M为二分图的一个匹配。
maximum matching:
当M的基数最大时，就为最大匹配.
free:
如果一个顶点v 不与M中任何一条边相连，即未参与匹配，则状态标记为free
augmenting path:
一条通路P=（v₁,v₂）,……(v_2k-1,v_2k)，
如果起点v₁与终点v_2k 均为free且P为交错路径则称P为M的增广路径。
shortest augmenting path:
如果增广路径P的基数最小，即拥有最少的边，则为最短增广路径。
vertex-disjoint
如果两个集合中不包含相同的顶点，则称之为顶点不相交的

二、相关定理及证明（离散数学差的同学可跳过此节）

LEMMA 1
如果P是匹配M的一个增广路径，则P⊕M为一个匹配，且|P⊕M|=|M|+1
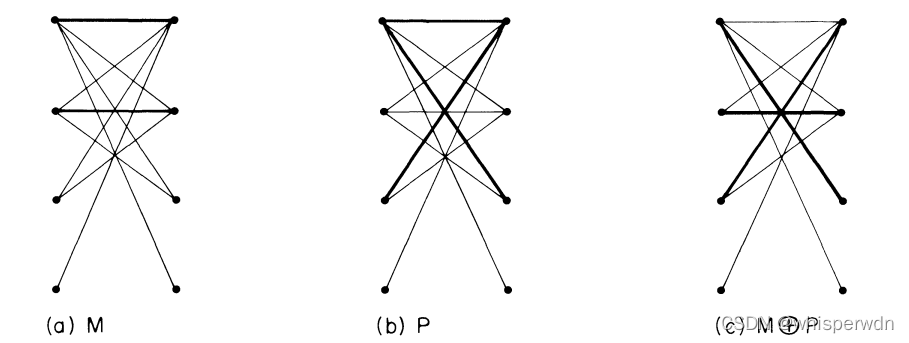
在这里插入图片描述
THEOREM 1
设M和N为匹配，如果|M|=r，|N|=s，s>r,那么M⊕N包含了至少s-r条匹配M的增长路径。
proof：
考虑一个图G’=(V,M⊕N),因为M和N均为匹配，那么每个顶点最多与M-N或N-M中的一条边相连，因此图G’的连通分支有下列三种情况：
（1）单悬挂点
（2）边含于M-N和N-M的一条回路
（3）边含于M-N和N-M的一条通路
设这些连通分支为C₁,C₂……，C_g,C_i = (V_i,E_i)
令α（C_i）= |E_i∩N| -|E_i∩M|则α（C_i）∈{-1，0，1}
当且仅当α（C_i）为1时C_i是M的一条增广路径
∑α（C_i）= |N-M|-|M-N|=|N|-|M|=s-r
因此共有至少s-r个连通分支使得α（C_i）=1，这些连通分支都是M的增广路径。
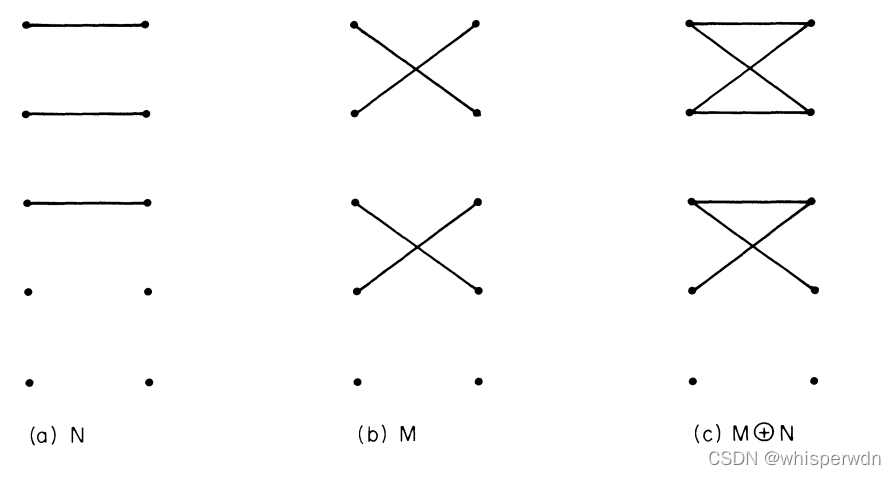
在这里插入图片描述
COROLLARY 1
当且仅当匹配M没有增广路径时M为最大匹配
COROLLARY 2
设|M|=r,最大匹配数为s,则存在一条M的长度<=2 ⌊r/(s-r)⌋+1 的增广路径
Proof
设N是一个最大匹配，则M⊕N包含了s-r条M的增广路径，这些路径一共最多包含r条M中的边，所以每一条路径最多包含最多 ⌊r/(s-r)⌋条M中的边，因此其最多有2 ⌊r/(s-r)⌋+1 条边
THEOREM 2
设M为一个匹配，P为M的一个最短增广路径，P’为P⊕M的一个增广路径，有
|P’|>= |P| +|P∩P’|
proof
令N = P⊕M⊕P’.则N为一个匹配且|N|=|M|+2,所以M⊕N包含两条M的增广路径（顶点不相交），令它们为P₁,P₂。因为M⊕N = P⊕P’,有 |P⊕P’|>=|P₁|+|P₂|.但因为P为M的最短增广路径，则|P₁|>=|P|,|P₂|>|P|.所以|P⊕P’|>=|P₁|+|P₂|>=2|P|.又因为
|P⊕P’|=|P|+|P‘|-|P∩P‘|，因此|P’|>= |P| +|P∩P’|
我们想象下列计算模式：从M₀=空集开始，计算一个序列M₀，M₁，M₂，……M_i，……，P_i是M_i的最短增广路径，M_i+1=M_i⊕P_i
COROLLARY 3
|P_i|<=|P_i+1|
COROLLARY 4
对于所有的i，j，如果|P_i|=|P_j|,则P_i和P_j是顶点不相交的
proof
反证法：设|P_i|=|P_j|,i<j,且顶点相交.那么存在k,l,使得i<=k<l<=j,P_k和P_l是顶点相交的，且对于每一个m,如果m满足k<m<l,则P_m和P_k，P_l都是顶点不相交的。那么P_l是M_k⊕P_k的一条增广路径，由定理二可知|P|>= |P_l| +|P_k∩P_l|。因为|P_k|=|P_l|,可得|P_k∩P_l|=0.由此可知P_k和P_l不包含相同的边。如果P_k和P_l包含相同的顶点v，则他们就会包含与之相关的M_k⊕P_k中的一条边，与事实不符。因此P_k和P_l是顶点不相交的，定理得证。
THEOREM 2
设最大匹配数为s,下列序列中不同整数的个数小于等于

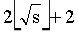
|P₀|，|P₁|，……|P_i|……
proof
令
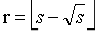
在这里插入图片描述
|M_r| = r由COROLLARY 2得

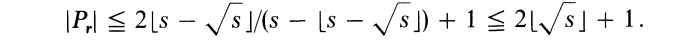
对于i<r,|P_i| 是小于等于

的一个正奇数，对于r<i<s,|P_i|是s-r个整数之一，故加起来总共是

三、算法描述

（1）对于一般图找最大匹配算法是从空集开始，找到M的所有最短增广路径（彼此顶点不相交），再将他们合并，重复执行，直至找不到增广路径为止。算法如下：
在这里插入图片描述

（2）对于二分图，有匈牙利算法
匈牙利算法不断为M寻找一条增广路径（不一定是最短增广路径），直至找不到增广路径为止，时间复杂度为O(n³)
以男女婚配为例
x_i代表男生，y_i代表女生
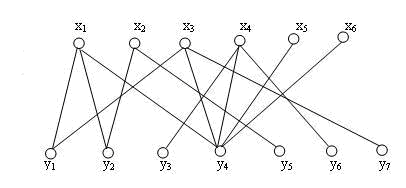
请添加图片描述
从x₁开始寻找增广路径

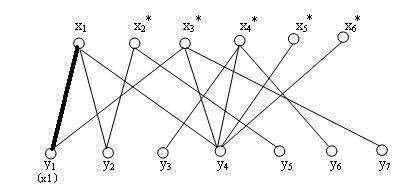
接下来是x₂

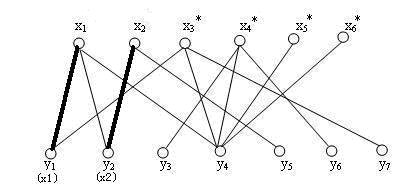
到x₃时，有多条路径可选，依赖于邻接表的存储方式，这里我们以邻接矩阵为例，选取
（x₃，y₁）（y₁,x₁）（x₁，y₂）（y₂,x₂）（x₂，y₅）

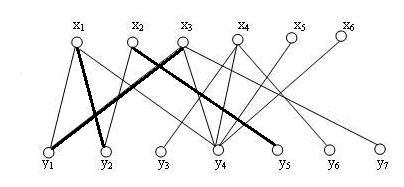
x₄,x₅,如法炮制最终得到一个最大匹配如图
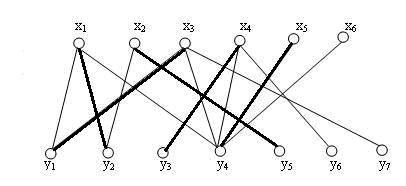
请添加图片描述
匈牙利算法实现如下：

bool Graph::match(int i)
{
    for (int j = 1; j <= N; ++j)
        if (adj[i][j] && !known[j]) //有边且未访问
        {
            known[j] = true;                 //记录状态为访问过
            if (p[j] == 0 || match(p[j])) //如果暂无匹配，或者原来匹配的左侧元素可以找到新的匹配
            {
                p[j] = i;    //当前左侧元素成为当前右侧元素的新匹配

                return true; //返回匹配成功
            }
        }
    return false; //循环结束，仍未找到匹配，返回匹配失败
}

int Graph::Hungarian()
{ 
    int cnt = 0;
    for(int i = 1; i <N+1; i++)
       p[i]=0;

    for (int i = 1; i <= M; i++)
    {
        for(int i = 1; i <N+1; i++)
            known[i]=false;
        if (match(i))
            cnt++;
    }

    return cnt;
}

（3）
现在我们讨论算法A在二分图里的实现，step1意在找到一个M的最短增广路径的集合。
为此，我们需要构造一个有向图，令E-M中的边从女生指向男生，M中的边从男生指向女生，即
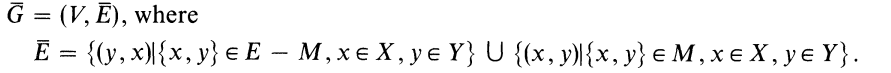
在这里插入图片描述
接下来我们找到其一个子图使得从一个free的女生开始，到一个free的男生结束，其余顶点均在M中，这就是M的一条最短增广路径。
借鉴我们解决最大流问题时的想法，类似的解决最大匹配问题

如下图，偶数层为男生，奇数层为女生,所有的free的女生位于L₀所有的free的男生位于
L₅，s指向所有free的男生，所有的free的女生指向t,这样就把寻找最短增广路径的集合类比为一个最大流问题
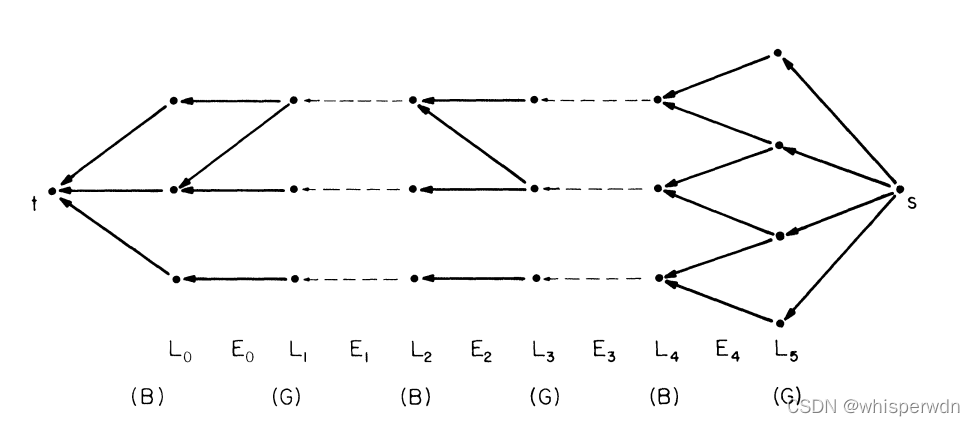
在这里插入图片描述
下面列出算法B的伪码实现

该算法的时间复杂度为
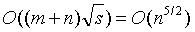
在这里插入图片描述
下面是我自己的算法实现供大家学习参考

void Graph::initialize()
{
    int i;
    cin>>M>>N>>Ne;
    vector<string> adj1,adj2;
    G.insert(pair<string,vector<string>>("s",adj1));

    for(i = 0; i < Ne; i++)
    {
        string p1, p2;
        cin>>p1>>p2;
        if(G.find(p1)==G.end()) {
            vector<string> adj;
            G.insert(pair<string,vector<string>>(p1,adj));
            G[p1].push_back("t");

        }

        if(G.find(p2)==G.end()) {
            vector<string> adj;
            G.insert(pair<string,vector<string>>(p2,adj));
            G["s"].push_back(p2);
        }
        if(known.find(p1)==known.end()) {
            known.insert(pair<string,bool>(p1,false));
        }
        if(known.find(p2)==known.end()) {
            known.insert(pair<string,bool>(p2,false));
        }
        known.insert(pair<string,bool>("t",false));
        // G[p1].push_back(p2);
        G[p2].push_back(p1);
    }

}

int Graph::max_match()
{   
    stack<string> STACK;
    STACK.push("s");
    string u,v;
    string FIRST;
    vector<string> B;
    int cnt = 0;
    bool flag = false;
    while(!STACK.empty())
    {
        u = STACK.top();
        //当此条路径不通时返回上层节点
        if(G[u].empty()) {
            while(G[STACK.top()].empty()) STACK.pop();
        }

        while(!G[u].empty()){
            FIRST = G[u].back();
            // 该节点未曾遍历
            if(!known[FIRST]) {
                if(FIRST!="t") {
                    STACK.push(FIRST);
                    known[FIRST] = true;
                    G[u].pop_back();
                    break;
                }else if(FIRST=="t"){//找到增广路径，立即输出
                    G[STACK.top()].pop_back();
                    while(STACK.top()!="s") {
                        v = STACK.top();
                        // cout<<v<<" ";
                        STACK.pop();
                        if(STACK.top()!="s")
                            G[v].push_back(STACK.top());
                    }
                    // cout<<endl;
                    cnt++;
                    for(auto iter = known.begin();iter!=known.end();iter++) iter->second=false;
                    known["t"] = false;
                    break;

                }
            }else G[u].pop_back();
        }
        if(G[STACK.top()].empty()&&(STACK.top()=="s")) break;
    }
    return cnt;
}

该算法本质上是匈牙利算法的非递归实现，但其结合了最大算法的思想，用栈存储，一旦某条边不能构成增广路径，便即删去，是以更为精妙，运行时间更快

J.E.Hopcroft and R.E.Karp,“An n^5/2Algorithm for Maximum Mathching in Biparartite Graphs”,SIAM Journal on Compuing,2(1973),135-158

whisperwdn

关注

2
点赞
踩
4

收藏

觉得还不错? 一键收藏
0
评论
二分图的最大匹配

一、定义matching:给定一个二分图G = (V,E)，M为E的子集，如果图中的顶点最多与M中的一条边相连，则称M为二分图的一个匹配。maximum matching:当M的基数最大时，就为最大匹配.free:如果一个顶点v 不与M中任何一条边相连，即未参与匹配，则状态标记为freeaugmenting path:一条通路P=（v1,v2）,……(v2k-1,v2k)如果起点v1与终点v2k 均为free且P为交错路径则称P为M的增广路径...
复制链接

扫一扫