我们在《》讲到:含有电容、电感的电路也是线性电路。其实这句话是存在瑕疵的,应该说当电感,电容中不储能,即其初始值为零的时候,电感,电容是线性元件(线性系统)。这个我们从线性系统的定义可以看出:
当一个系统满足ay=ax时,通俗的讲就是当其输入增加或减少a倍,其输出同时也增加或减少a倍时,就说这个系统是线性系统。
依据上面的定义,我们看下电容的公式:
当我们以u为输入,i为输出的时候
i
(
t
)
=
c
∗
d
u
d
t
i(t) =c*\frac{du}{dt}
i(t)=c∗dtdu
这个系统就是线性系统,但是这个时候也不存在初始值的概念了。因为自变量就是u。
当我们以i为输入,u为输出的时候
u
(
t
)
=
1
c
∗
∫
0
t
i
(
t
)
d
t
+
u
(
0
)
 
u(t) =\frac1c *\int_0^t i(t)dt+u(0)\,
u(t)=c1∗∫0ti(t)dt+u(0)
这个时候当
i
(
t
)
i(t)
i(t)变为原来的两倍时,很显然我们不能直接得到
u
(
t
)
u(t)
u(t)也是原来的两倍。这就不是一个线性的系统。
并且在实际的电路中,我们很难以一个电压直接作为电容的自变量。例如
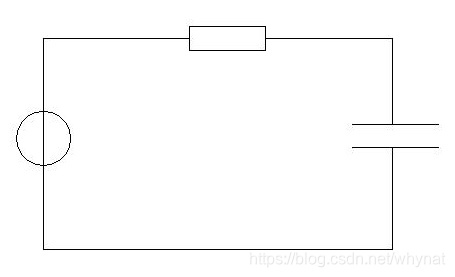
在这个电路中,如果我们用电容的电流做方程,会得到
u
s
(
t
)
=
i
(
t
)
∗
r
+
∫
0
t
i
(
t
)
d
t
+
u
(
0
)
 
u_s(t) =i(t)*r +\int_0^t i(t)dt+u(0)\,
us(t)=i(t)∗r+∫0ti(t)dt+u(0)
这样做是得不到微分方程,没法求解的。
因此我们只能列下面的微分方程
u
s
(
t
)
=
u
c
+
r
∗
c
d
u
d
t
u_s(t) =u_c +r*c\frac{du}{dt}
us(t)=uc+r∗cdtdu
我们注意观察这个方程,其解得的值为
u
c
=
u
0
∗
e
−
t
r
c
+
u
s
(
1
−
e
−
t
r
c
)
u_c =u_0*e^{- \frac{t}{rc}}+u_s(1-e^{-\frac{t}{rc}})
uc=u0∗e−rct+us(1−e−rct)
也就是说这个系统的输出是电容电压,输入是电源电压,这个系统是非线性的。那么我们就不能利用叠加定理了吗,其实不是的,
注意观察,上面式子的右边是线性的,且只与电源电压有关,左边是电容的零输入响应。
其实左边的部分可以写为
u
0
∗
e
−
t
r
c
=
u
0
∗
δ
∗
(
1
−
e
−
t
r
c
)
u_0*e^{- \frac{t}{rc}}=u_0*\delta*(1-e^{-\frac{t}{rc}})
u0∗e−rct=u0∗δ∗(1−e−rct)
其中的
δ
\delta
δ为单位冲激激励,其积分值为1。也就是说:电容的零输入响应其实相当于冲激激励的零状态响应(冲激量的积分为电容的初始值)
这就巧妙的避开了电容初始值的问题。其实在电路教材里面,我们已经知道了电路的全响应=零状态响应+零输入响应。这就是我们在利用叠加定理时需要注意的。
总结
带有初始值的电容,电感组成的系统可以看做是线性系统,也可以利用叠加定理求解,但是要考虑系统的零输入响应。
我们在利用叠加定理的时候,可以将电容的初始值置零,然后计算所有激励的响应,叠加起来。这个时候注意,我们还要将所有激励置零,然后计算在电容初始值条件下的零输入响应,最后将两部分叠加起来就是电容的实际响应。
即:
全响应=电容置零时电源1的零状态响应+电容置零时电源2的零状态响应+电容置零时电源n的零状态响应+电源置零时的电容的零输入响应。
其实从另一个角度考虑,电源置零时的电容的零输入响应其实相当于电容置零时,冲激电源的响应(冲激量的积分为电容的初始值)
那么上面的式子可以写为:
全响应=电容置零时电源1的零状态响应+电容置零时电源2的零状态响应+电容置零时电源n的零状态响应+电容置零时的冲激响应
因为都是电容置零,所以简写为:
全响应=电源1的零状态响应+电源2的零状态响应+电源n的零状态响应+冲激响应(冲激量的积分为电容的初始值)
另外还可以写为:
全响应=电源1全响应+电源2的零状态响应+电源n的零状态响应
也就是说:在电路中运用叠加定理时,储能元件(电容,电感)的初始值只能计算一次
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








