第16章 强化学习
16.1 任务与奖赏
强化学习任务通常用马尔可夫决策过程(Markov Decision Process,MDP)来描述:及其处于缓解E中,状态空间为X,其中每个状态x∈Xx \in Xx∈X是机器感知到缓解的描述,机器能采取的动作构成了动作空间A,若某个动作a∈Aa \in Aa∈A作用在当前状态xxx上,则潜在的转移函数PPP将使得环境从当前状态按某种概率转移到另一种状态。
在转移到另一个状态的同时,环境会根据潜在的奖赏(reward)函数RRR反馈给机器一个奖赏。
强化学习任务对应了四元组E=⟨X,A,P,R⟩E = \left\langle X,A,P,R \right\rangleE=⟨X,A,P,R⟩,其中P:X×A×X→RP:X \times A \times X \rightarrow RP:X×A×X→R指定了状态转移概率;R:X×A×X→RR:X \times A \times X\mathbb{\rightarrow R}R:X×A×X→R指定了奖赏。
机器通过在环境中不断地尝试而学得一个策略π\piπ,根据这个策略,在状态xxx下就能得知要执行的动作a=π(x)a = \pi\left( x \right)a=π(x)。策略的两种表示方法:一种是将策略表示为函数π:X→A\pi:X \rightarrow Aπ:X→A,确定性策略常用这种表示;另一种是概率表示π:X×A→R\pi:X \times A\mathbb{\rightarrow R}π:X×A→R,随机性策略常用这种表示,π(x,a)\pi\left( x,a \right)π(x,a)为状态xxx下选择动作aaa的概率,这里必须有∑aπ(x,a)=1\sum_{a}^{}{\pi\left( x,a \right) = 1}∑aπ(x,a)=1
16.2 K-摇臂赌博机
16.2.1 探索与利用
欲最大化单步奖赏考虑:1、需要知道每个动作带来的奖赏;2、执行奖赏最大的动作
K-摇臂赌博机(K-armed bandit):单步强化学习任务对应的理论模型
仅探索法:将所有的尝试机会平均分配给每个摇臂,最后以每个摇臂各自的平均吐币概率作为其奖赏期望的近似估计。
仅利用法:按下目前最优的摇臂,若有多个摇臂同时为最优,则从中随机选取一个。
16.2.2 ϵ\mathbf{\epsilon}ϵ-贪心
ϵ\epsilonϵ-贪心法基于概率来对探索和利用进行折中:每次尝试时,以ϵ\epsilonϵ的概率进行探索,以1−ϵ1- \epsilon1−ϵ的概率进行利用。
令Q(k)Q\left( k \right)Q(k)记录摇臂kkk的平均奖赏。若摇臂kkk被尝试nnn次,得到的奖赏为v1,v2,…,vnv_{1},v_{2},\ldots,v_{n}v1,v2,…,vn,平均奖赏为
Q(k)=1n∑i=1nvi
Q\left( k \right) = \frac{1}{n}\sum_{i = 1}^{n}v_{i}
Q(k)=n1i=1∑nvi

16.2.3 Softmax
Softmax算法基于当前已知的摇臂平均奖赏来对探索和利用进行折中。若个摇臂的平均奖赏相当,则选取各摇臂的概率也相当;若某些摇臂的平均奖赏明显高于其他摇臂,则它们被选取的概率也明显高。
Softmax算法中的摇臂概的分配是基于Boltzmann分布
P(k)=eQ(k)τ∑i=1KeQ(i)τ P\left( k \right) = \frac{e^{\frac{Q\left( k \right)}{\tau}}}{\sum_{i = 1}^{K}e^{\frac{Q\left( i \right)}{\tau}}} P(k)=∑i=1KeτQ(i)eτQ(k)
其中Q(i)Q\left( i \right)Q(i)记录当前摇臂的平均奖赏

16.3 有模型学习
16.3.1 策略评估
令函数Vπ(x)V^{\pi}\left( x \right)Vπ(x)表示从状态xxx出发,使用策略π\piπ所带来的累积奖赏,函数Qπ(x,a)Q^{\pi}\left( x,a \right)Qπ(x,a)表示从状态xxx出发,执行动作aaa后再使用策略π\piπ所带来的累积奖赏。V(.)V\left( . \right)V(.)为状态值函数,Q(.)\left( . \right)(.)为状态-动作值函数。
由累积奖赏的定义,有状态值函数
{VTπ(x)=Eπ[ 1T∑i=1Trt∣x0=x],TVγπ(x)=Eπ[ ∑i=1+∞γtrt+1∣x0=x],γ \left\{ \begin{matrix} V_{T}^{\pi}\left( x \right) = \mathbb{E}_{\pi}\left\lbrack \left. \ \frac{1}{T}\sum_{i = 1}^{T}r_{t} \right|x_{0} = x \right\rbrack,T \\ V_{\gamma}^{\pi}\left( x \right) = \mathbb{E}_{\pi}\left\lbrack \left. \ \sum_{i = 1}^{+ \infty}{\gamma^{t}r}_{t + 1} \right|x_{0} = x \right\rbrack,\gamma \\ \end{matrix} \right.\ {VTπ(x)=Eπ[ T1∑i=1Trt∣∣∣x0=x],TVγπ(x)=Eπ[ ∑i=1+∞γtrt+1∣∣x0=x],γ
令x0x_{0}x0表示起始状态,a0a_{0}a0表示起始状态上采取的第一个动作,对于T步累积奖赏,则有状态-动作值函数
{QTπ(x,a)=Eπ[ 1T∑i=1Trt∣x0=x,a0=a]Qγπ(x,a)=Eπ[ ∑i=1+∞γtrt+1∣x0=x,a0=a] \left\{ \begin{matrix} Q_{T}^{\pi}\left( x,a \right) = \mathbb{E}_{\pi}\left\lbrack \left. \ \frac{1}{T}\sum_{i = 1}^{T}r_{t} \right|x_{0} = x,a_{0} = a \right\rbrack \\ Q_{\gamma}^{\pi}\left( x,a \right) = \mathbb{E}_{\pi}\left\lbrack \left. \ \sum_{i = 1}^{+ \infty}{\gamma^{t}r}_{t + 1} \right|x_{0} = x,a_{0} = a \right\rbrack \\ \end{matrix} \right.\ {QTπ(x,a)=Eπ[ T1∑i=1Trt∣∣∣x0=x,a0=a]Qγπ(x,a)=Eπ[ ∑i=1+∞γtrt+1∣∣x0=x,a0=a]
则T步累积奖赏有
VTπ(x)=Eπ[ 1T∑i=1Trt∣x0=x] V_{T}^{\pi}\left( x \right) = \mathbb{E}_{\pi}\left\lbrack \left. \ \frac{1}{T}\sum_{i = 1}^{T}r_{t} \right|x_{0} = x \right\rbrack VTπ(x)=Eπ[ T1i=1∑Trt∣∣∣∣∣x0=x]
=Eπ[ 1Tr1+T−1T1T−1∑i=2Trt∣x0=x] = \mathbb{E}_{\pi}\left\lbrack \left. \ \frac{1}{T}r_{1} + \frac{T - 1}{T}\frac{1}{T - 1}\sum_{i = 2}^{T}r_{t} \right|x_{0} = x \right\rbrack =Eπ[ T1r1+TT−1T−11i=2∑Trt∣∣∣∣∣x0=x]
=∑a∈Aπ(x,a)∑x′∈XPx→x′a(1TRx→x′a+T−1TEπ[ 1T−1∑i=1T−1rt∣x0=x′]) = \sum_{a \in A}^{}{\pi\left( x,a \right)\sum_{x^{'} \in X}^{}{P_{x \rightarrow x^{'}}^{a}\left( \frac{1}{T}R_{x \rightarrow x^{'}}^{a} + \frac{T - 1}{T}\mathbb{E}_{\pi}\left\lbrack \left. \ \frac{1}{T - 1}\sum_{i = 1}^{T - 1}r_{t} \right|x_{0} = x' \right\rbrack \right)}} =a∈A∑π(x,a)x′∈X∑Px→x′a(T1Rx→x′a+TT−1Eπ[ T−11i=1∑T−1rt∣∣∣∣∣x0=x′])
=∑a∈Aπ(x,a)∑x′∈XPx→x′a(1TRx→x′a+TT−1VT−1π(x′)) = \sum_{a \in A}^{}{\pi\left( x,a \right)\sum_{x^{'} \in X}^{}{P_{x \rightarrow x^{'}}^{a}\left( \frac{1}{T}R_{x \rightarrow x^{'}}^{a} + \frac{T}{T - 1}V_{T - 1}^{\pi}\left( x^{'} \right) \right)}} =a∈A∑π(x,a)x′∈X∑Px→x′a(T1Rx→x′a+T−1TVT−1π(x′))
类似的,对于γ\gammaγ折扣累积奖赏有
Vγπ(x)=∑a∈Aπ(x,a)∑x′∈XPx→x′a(Rx→x′a+γVγπ(x′))
V_{\gamma}^{\pi}\left( x \right) = \sum_{a \in A}^{}{\pi\left( x,a \right)\sum_{x^{'} \in X}^{}{P_{x \rightarrow x^{'}}^{a}\left( R_{x \rightarrow x^{'}}^{a} + \gamma V_{\gamma}^{\pi}\left( x^{'} \right) \right)}}
Vγπ(x)=a∈A∑π(x,a)x′∈X∑Px→x′a(Rx→x′a+γVγπ(x′))

则状态-动作值函数
{QTπ(x,a)=∑x′∈XPx→x′a(1TRx→x′a+TT−1VT−1π(x′))Qγπ(x,a)=∑x′∈XPx→x′a(Rx→x′a+γVγπ(x′)) \left\{ \begin{matrix} Q_{T}^{\pi}\left( x,a \right) = \sum_{x^{'} \in X}^{}{P_{x \rightarrow x^{'}}^{a}\left( \frac{1}{T}R_{x \rightarrow x^{'}}^{a} + \frac{T}{T - 1}V_{T - 1}^{\pi}\left( x^{'} \right) \right)} \\ Q_{\gamma}^{\pi}\left( x,a \right) = \sum_{x^{'} \in X}^{}{P_{x \rightarrow x^{'}}^{a}\left( R_{x \rightarrow x^{'}}^{a} + \gamma V_{\gamma}^{\pi}\left( x^{'} \right) \right)} \\ \end{matrix} \right.\ ⎩⎨⎧QTπ(x,a)=∑x′∈XPx→x′a(T1Rx→x′a+T−1TVT−1π(x′))Qγπ(x,a)=∑x′∈XPx→x′a(Rx→x′a+γVγπ(x′))
16.3.2 策略改进
理想的策略响应能最大化累积奖赏
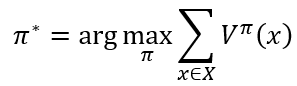
一个强化学习任务可能有多个最优策略,最优策略所对应的值函数V∗V^{*}V∗称为最优值函数,即
∀x∈X:V∗(x)=Vπ∗(x) \forall x \in X:V^{*}\left( x \right) = V^{\pi^{*}}\left( x \right) ∀x∈X:V∗(x)=Vπ∗(x)
对累积奖赏进行改进
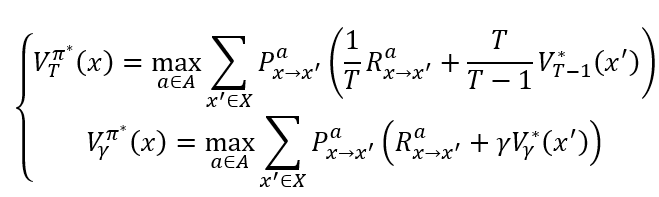
即改进后为
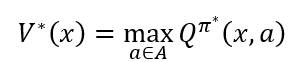
则最优状态-动作值函数
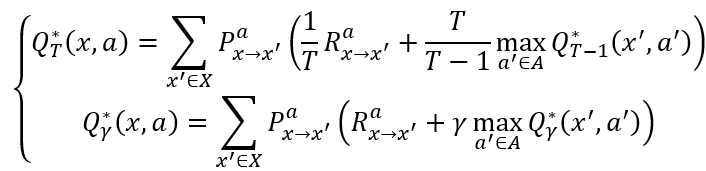
最优Bellman等式揭示了非最优策略的改进方式:将策略选择的动作改进为当前最优的动作。
16.3.3 策略迭代与值迭代
策略迭代(policy iteration):从一个初始策略出发,先进行策略评估,然后改进策略,评估改进的策略,再进一步改进策略,……不断迭代进行测量评估和改进,直到测量收敛、不再改变为止。

则值函数的改进为
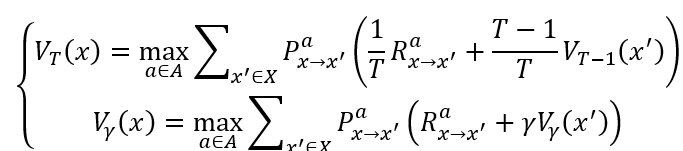

16.4 免模型学习
免模型学习(model-free learning):若学习算法不依赖于环境建模
16.4.1 蒙特卡罗强化学习
同策略蒙特卡罗强化学习算法
算法中奖赏均值采用增量式计算,每采样出一条轨迹,就根据该轨迹涉及的所有状态-动作对来对值函数进行更新

函数fff在概率分布ppp的期望可表达为
E[f]=∫xp(x)f(x)dx \mathbb{E}\left\lbrack f \right\rbrack = \int_{x}^{}{p\left( x \right)f\left( x \right)\text{dx}} E[f]=∫xp(x)f(x)dx
可通过从概率分布ppp上的采样{x1,x2,…,xm}\left\{ x_{1},x_{2},\ldots,x_{m} \right\}{x1,x2,…,xm}来估计fff的期望,即
E^[f]=1m∑i=1mf(x) \hat{\mathbb{E}}\left\lbrack f \right\rbrack = \frac{1}{m}\sum_{i = 1}^{m}{f\left( x \right)} E^[f]=m1i=1∑mf(x)
若引入另一个分布qqq,则函数fff在概率分布ppp下的期望为
E[f]=∫xq(x)p(x)q(x)f(x)dx \mathbb{E}\left\lbrack f \right\rbrack = \int_{x}^{}{q\left( x \right)\frac{p\left( x \right)}{q\left( x \right)}f\left( x \right)\text{dx}} E[f]=∫xq(x)q(x)p(x)f(x)dx
上式可看作p(x)q(x)f(x)\frac{p\left( x \right)}{q\left( x \right)}f\left( x \right)q(x)p(x)f(x)在分布qqq下的期望,因此通过在qqq上的采样{x1′,x2′,…,xm′}\left\{ x_{1}^{'},x_{2}^{'},\ldots,x_{m}^{'} \right\}{x1′,x2′,…,xm′}可估计为
E^[f]=1m∑i=1mp(xi′)q(xi′)f(xi′) \hat{\mathbb{E}}\left\lbrack f \right\rbrack = \frac{1}{m}\sum_{i = 1}^{m}\frac{p\left( x_{i}^{'} \right)}{q\left( x_{i}^{'} \right)}f\left( x_{i}^{'} \right) E^[f]=m1i=1∑mq(xi′)p(xi′)f(xi′)
对累积奖赏估计期望
Q(x,a)=1m∑i=1mRi Q\left( x,a \right) = \frac{1}{m}\sum_{i = 1}^{m}R_{i} Q(x,a)=m1i=1∑mRi
其中RiR_{i}Ri表示第iii条轨迹上自状态xxx至结束的累积奖赏。
若改用策略π′\pi^{'}π′的采样轨迹来评估策略π\piπ,则仅需对累积奖赏加权,即
Q(x,a)=1m∑i=1mPiπPiπ′Ri Q\left( x,a \right) = \frac{1}{m}\sum_{i = 1}^{m}{\frac{P_{i}^{\pi}}{P_{i}^{\pi^{'}}}R_{i}} Q(x,a)=m1i=1∑mPiπ′PiπRi
其中PiπP_{i}^{\pi}Piπ和Piπ′P_{i}^{\pi^{'}}Piπ′分别表示两个策略产生第iii条轨迹的概率
对于给定的一条轨迹⟨x0,a0,r1,…,xT−1,aT−1,rT,xT⟩\left\langle x_{0},a_{0},r_{1},\ldots,x_{T - 1},a_{T - 1},r_{T},x_{T} \right\rangle⟨x0,a0,r1,…,xT−1,aT−1,rT,xT⟩,策略π\piπ产生该轨迹的概率为
Pπ=∏i=0T−1π(xi,ai)Pxi→xi+1ai P^{\pi} = \prod_{i = 0}^{T - 1}{\pi\left( x_{i},a_{i} \right)P_{x_{i} \rightarrow x_{i + 1}}^{a_{i}}} Pπ=i=0∏T−1π(xi,ai)Pxi→xi+1ai
两个策略概率的比值
PπPπ′=∏i=0T−1π(xi,ai)π′(xi,ai)
\frac{P^{\pi}}{P^{\pi^{'}}} = \prod_{i = 0}^{T - 1}\frac{\pi\left( x_{i},a_{i} \right)}{\pi^{'}\left( x_{i},a_{i} \right)}
Pπ′Pπ=i=0∏T−1π′(xi,ai)π(xi,ai)

16.4.2 时序差分学习
时序差分学习(Temporal Difference,TD):结合了动态规划与蒙特卡罗方法的思想,能做到更高效的免模型学习。
蒙特卡罗强化学习算法的本质:通过多次尝试后求平均作为期望累积奖赏的近似,但它在求平均时是批处理式进行的,即在一个完整的采样轨迹完成后再对所有的状态-动作对进行更新。


16.5 值函数近似
表格值函数(tabular value function):值函数能表示为一个数值,输入iii对应的函数值就是数值元素iii的值,且更改一个状态上的值不会影响其他状态上的值。
假定状态空间为n维实数空间X=RnX = \mathbb{R}^{n}X=Rn,值函数能表达为状态的线性函数
Vθ(x)=θTx V_{\theta}\left( x \right) = \theta^{T}x Vθ(x)=θTx
其中xxx为状态向量,θ\thetaθ为参数向量。
值函数尽可能近似真实值函数VπV^{\pi}Vπ,用最小二乘误差来度量
Eθ=Ex∼π[(Vπ(x)−Vθ(x))2] E_{\theta} = \mathbb{E}_{x\sim\pi}\left\lbrack \left( V^{\pi}\left( x \right) - V_{\theta}\left( x \right) \right)^{2} \right\rbrack Eθ=Ex∼π[(Vπ(x)−Vθ(x))2]
其中Ex∼π\mathbb{E}_{x\sim\pi}Ex∼π表示由策略π\piπ所采样而得的状态上的期望。
为了使误差最小化,采用梯度下降法,对误差求负导数
−∂Eθ∂θ=Ex∼π[2(Vπ(x)−Vθ(x))∂Vθ(x)∂θ]=Ex∼π[2(Vπ(x)−Vθ(x))x]- \frac{\partial E_{\theta}}{\partial\theta} = \mathbb{E}_{x\sim\pi}\left\lbrack 2\left( V^{\pi}\left( x \right) - V_{\theta}\left( x \right) \right)\frac{\partial V_{\theta}\left( x \right)}{\partial\theta} \right\rbrack = \mathbb{E}_{x\sim\pi}\left\lbrack 2\left( V^{\pi}\left( x \right) - V_{\theta}\left( x \right) \right)x \right\rbrack −∂θ∂Eθ=Ex∼π[2(Vπ(x)−Vθ(x))∂θ∂Vθ(x)]=Ex∼π[2(Vπ(x)−Vθ(x))x]
可得到对应单样本的更新规则
θ=θ+α(Vπ(x)−Vθ(x))x \theta = \theta + \alpha\left( V^{\pi}\left( x \right) - V_{\theta}\left( x \right) \right)x θ=θ+α(Vπ(x)−Vθ(x))x
基于Vπ(x)=r+γVπ(x′)V^{\pi}\left( x \right) = r + \gamma V^{\pi}\left( x^{'} \right)Vπ(x)=r+γVπ(x′)用当前估计的值函数代替真实值函数,即
θ=θ+αVθ(r+γVθ(x′)−Vθ(x))x=θ+α(r+γx′−θTx)x \theta = \theta + \alpha V_{\theta}\left( r + \gamma V_{\theta}\left( x^{'} \right) - V_{\theta}\left( x \right) \right)x = \theta + \alpha\left( r + \gamma x^{'} - \theta^{T}x \right)x θ=θ+αVθ(r+γVθ(x′)−Vθ(x))x=θ+α(r+γx′−θTx)x
其中x′x^{'}x′是下一时刻的状态

16.6 模仿学习
16.6.1 直接模仿学习
直接模仿学习:直接模仿人类专家的状态-动作对可环境多步决策。
假定获得一批人类专家的决策轨迹数据{τ1,τ2,…,τm}\left\{ \tau_{1},\tau_{2},\ldots,\tau_{m} \right\}{τ1,τ2,…,τm},每条轨迹包含状态和动作序列
τi=⟨s1i,a1i,s2i,a2i,…,sni+1i⟩ \tau_{i} = \left\langle s_{1}^{i},a_{1}^{i},s_{2}^{i},a_{2}^{i},\ldots,s_{n_{i} + 1}^{i} \right\rangle τi=⟨s1i,a1i,s2i,a2i,…,sni+1i⟩
其中nin_{i}ni为第iii条轨迹中的转移次数。
将所有轨迹上的所有状态-动作对抽取,构造出一个新的数据集合
D={(s1,a1),(s2,a2),…,(s∑i=1mni,a∑i=1mni)} D = \left\{ \left( s_{1},a_{1} \right),\left( s_{2},a_{2} \right),\ldots,\left( s_{\sum_{i = 1}^{m}n_{i}},a_{\sum_{i = 1}^{m}n_{i}} \right) \right\} D={(s1,a1),(s2,a2),…,(s∑i=1mni,a∑i=1mni)}
然后对这个新构造出的数据集合D使用分类或回归算法即可学得策略模型。学得的这个策略模型可作为机器进行强化学习的初始策略,再通过强化学习方法基于环境反馈进行改进,从而获得更好的策略。
16.6.2 逆强化学习
寻找某种奖赏函数使得范例数据是最优的,然后即可使用这个奖赏函数来训练强化学习策略。
假设奖赏函数能表达为状态特征的线性函数,即R(x)=ωTxR\left( x \right) = \omega^{T}xR(x)=ωTx。于是策略π\piπ的累积奖赏为
ρπ=E[∑t=0+∞γtR(xt)∣π ]=E[∑t=0+∞γtωTxt∣π ]=ωTE[∑t=0+∞γtxt∣π ] \rho^{\pi} = \mathbb{E}\left\lbrack \sum_{t = 0}^{+ \infty}{\gamma^{t}R\left( x_{t} \right)\left| \pi \right.\ } \right\rbrack\mathbb{= E}\left\lbrack \sum_{t = 0}^{+ \infty}{\gamma^{t}\omega^{T}x_{t}\left| \pi \right.\ } \right\rbrack = \omega^{T}\mathbb{E}\left\lbrack \sum_{t = 0}^{+ \infty}{\gamma^{t}x_{t}\left| \pi \right.\ } \right\rbrack ρπ=E[t=0∑+∞γtR(xt)∣π ]=E[t=0∑+∞γtωTxt∣π ]=ωTE[t=0∑+∞γtxt∣π ]
即状态向量加权和的期望与系数ω\omegaω的内积。
将状态向量的期望E[∑t=0+∞γtxt∣π ]\mathbb{E}\left\lbrack \sum_{t = 0}^{+ \infty}{\gamma^{t}x_{t}\left| \pi \right.\ } \right\rbrackE[∑t=0+∞γtxt∣π ]简写为x‾π{\overset{\overline{}}{x}}^{\pi}xπ,将每条范例轨迹上的状态加权求和再平均,记为x‾∗{\overset{\overline{}}{x}}^{*}x∗。对于最优奖赏函数R(x)=ω∗TxR\left( x \right) = \omega^{*T}xR(x)=ω∗Tx和任意其他策略产生的x‾π{\overset{\overline{}}{x}}^{\pi}xπ,有
ω∗Tx‾∗−ω∗Tx‾π=ω∗T(x‾∗−x‾π)≥0 \omega^{*T}{\overset{\overline{}}{x}}^{*} - \omega^{*T}{\overset{\overline{}}{x}}^{\pi} = \omega^{*T}\left( {\overset{\overline{}}{x}}^{*} - {\overset{\overline{}}{x}}^{\pi} \right) \geq 0 ω∗Tx∗−ω∗Txπ=ω∗T(x∗−xπ)≥0
若能对所有策略计算出(x‾∗−x‾π)\left( {\overset{\overline{}}{x}}^{*} -
{\overset{\overline{}}{x}}^{\pi} \right)(x∗−xπ),即可解出:
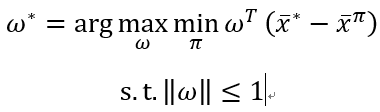






 本文围绕强化学习展开,介绍其用马尔可夫决策过程描述及对应四元组。阐述K - 摇臂赌博机的探索与利用方法,如ϵ - 贪心、Softmax算法。还讲解有模型学习的策略评估、改进与迭代,免模型学习的蒙特卡罗强化学习和时序差分学习,以及值函数近似、模仿学习等内容。
本文围绕强化学习展开,介绍其用马尔可夫决策过程描述及对应四元组。阐述K - 摇臂赌博机的探索与利用方法,如ϵ - 贪心、Softmax算法。还讲解有模型学习的策略评估、改进与迭代,免模型学习的蒙特卡罗强化学习和时序差分学习,以及值函数近似、模仿学习等内容。
















 3599
3599

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








