二分搜索树
定义
二分搜索树(Binary Search Tree),也称二叉查找树,有序二叉树,排序二叉树,是指一棵空树或者具有下列性质的二叉树:
- 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 任意节点的左、右子树也分别为二叉查找树。
没有键值相等的节点(no duplicate nodes)。
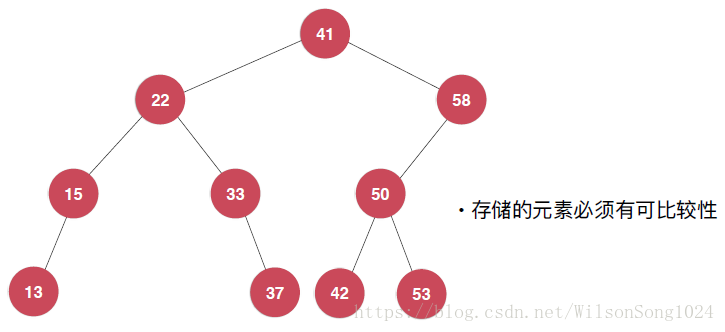
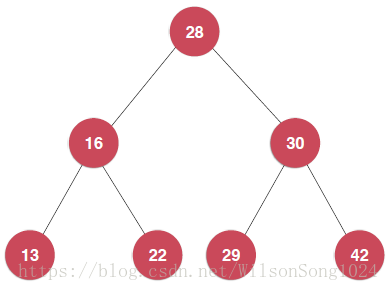
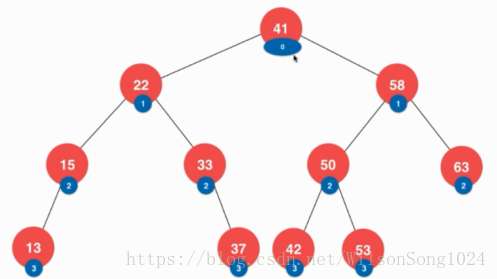
如下图就是一个二分搜索树,其本质就是一个二叉树,并且不一定是满的,而且元素要可比较大小。
优势
二分搜索树在某些方面是具有优势的,比如我们从时间复杂度上来分析一下:
实现
二分搜索树的实现
简单的实现一下,通过一个私有类实现包含其所需的节点,值,左节点,右节点。
public class BinarySearchTree<E extends Comparable<E>> {
/**
* 定义树节点的私有类
* @param <E>
*/
private class Node{
public E e;
public Node left, right;
public Node(E e){
this.e = e;
left = null;
right = null;
}
}
private Node root; //根节点
private int size; //树的大小
public BinarySearchTree(){
root = null;
size = 0;
}向树中添加元素
其实插入元素使用递归的方式很容易,其核心思想:从根节点开始找插入的位置,满足二叉搜索树的特性,比左子节点大,比右子节点小.
具体的步骤:
从根节点开始,先比较当前节点,如果当前节点为null那么很明显就应该插入到这个节点。
如果上面的节点不是null,那么和当前节点比较,如果小于节点就往左子树放,如果大于节点就往右子树放。
然后分别对左子树或者右子树递归的递归进行如上1、2步骤的操作
此时就用到了递归,那么递归是对某一个问题,它的子问题需要是同样的模型。此处的一个小的问题就是:对某个node,然后进行操作,所以参数应该有个node才能实现循环起来。此处向以node为根的二叉搜索树中,插入节点value.
/**
* 添加元素
* @param e 添加的元素
*/
public void add(E e){
root = add(root, e);
}
/**
* 递归的添加元素
* 向以node为根的二分搜索树中插入元素e,递归算法
* 返回插入新节点后二分搜索树的根
* @param node 树节点
* @param e 元素
* @return
*/
private Node add(Node node, E e){
if (node == null){
size ++;
return new Node(e);
}
if (e.compareTo(node.e) > 0){
node.right = add(node.right, e);
}
if (e.compareTo(node.e) < 0){
node.left= add(node.left, e);
}
return node;
}
注意
在这里抠一下关于递归添加元素这个函数为啥要返回插入新节点后二分搜索树的根,
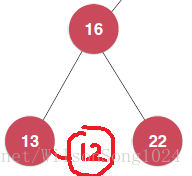
比方说上面这棵树,我要添加元素12,执行递归的第一步之后,node节点其实是28这个根节点,然后执行
add(node.left, e);
其实就是像下面的树中添加元素,但是现在的节点还是28,执行完之后就是下面这棵树,返回以16为根节点的这棵树,然后赋值给node.left。其实就是相当于把这棵树连接到了28这个节点上。最后返回node也就是28这个节点,其实就是新添加元素之后的树。
查询树中包含某一个元素
其实查询包含树中是否包含某个元素与向树中添加一个元素的思路是类似的,都是通过递归的方式查询左右子树。
/**
* 查询是否包含元素
* @param e 元素
* @return
*/
public boolean contain(E e){
return contains(root, e);
}
/**
* 递归的查询是否包含某个元素
* @param node 树节点
* @param e 元素
* @return
*/
private boolean contains(Node node, E e){
if (node == null){
return false;
}
if (e.compareTo(node.e) < 0){
return contains(node.left, e);
}else if (e.compareTo(node.e) > 0){
return contains(node.right, e);
}else {
return true;
}
}树的遍历
其实树的遍历和图的遍历是一样的,分为两种,一种是广度优先遍历,一种是深度优先遍历。
深度优先遍历
深度优先遍历又分为三种:
前序遍历(Preorder Traversal):先访问当前节点,再依次递归访问左右子树
中序遍历(Inorder Traversal):先递归访问左子树,再访问自身,再递归访问右子树
后序遍历(Postorder Traversal):先递归访问左右子树,最后再访问当前节点。
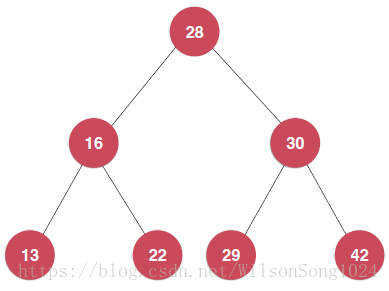
比如一棵树:
前序遍历的结果是:28–16–13–22–30–29–42
中序遍历的结果是:13–16–22–28–30–29–42
后序遍历的结果是:13–22–16–29–42–30–28
前序遍历的递归实现
递归实现的思想是非常简单的,从根节点开始,判断根节点是否有值,有则输出,然后递归的去处理器左子树,最后去处理其右子树。
/**
* 前序遍历
*/
public void preOrder(){
preOrder(root);
}
/**
* 递归前序遍历
* @param node
*/
public void preOrder(Node node){
if (node == null){
return;
}else {
System.out.println(node.e);
preOrder(node.left);
preOrder(node.right);
}
}前序遍历的非递归实现
关于前序遍历的非递归实现这里使用栈的方式,具体的思路如下:
具体的实现其实就是从根节点开始向堆栈中压入元素,然后弹出元素,然将该根节点的左右孩子按顺序压入堆栈,然后弹出栈顶元素,在将弹出的元素的左右孩子按顺序压入堆栈,不断的执行,直到树中没有元素,堆栈中就只弹出元素,直至堆栈为空。
具体的实现如下:
/**
* 非递归的实现二分搜索树的前序遍历
*/
public void preOrderNR(){
Stack<Node> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()){
Node cur = stack.pop();
System.out.println(cur.e);
if (cur.right != null){
stack.push(cur.right);
}
if (cur.left != null){
stack.push(cur.left);
}
}
}中序遍历的递归实现
/**
* 中序遍历
*/
public void inOrder(){
inOrder(root);
}
/**
* 递归的实现中序遍历
* @param node 节点
*/
public void inOrder(Node node){
if(node == null)
return;
inOrder(node.left);
System.out.println(node.e);
inOrder(node.right);
}后序遍历的递归实现
/**
* 后序遍历
*/
public void postOrder(){
postOrder(root);
}
/**
* 递归的实现后序遍历
* @param node 节点
*/
private void postOrder(Node node){
if(node == null)
return;
postOrder(node.left);
postOrder(node.right);
System.out.println(node.e);
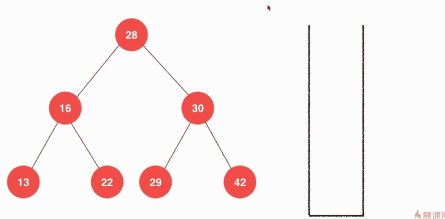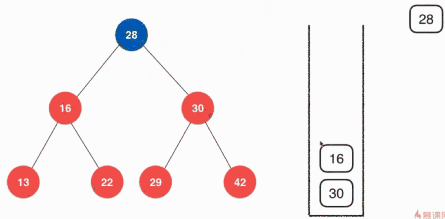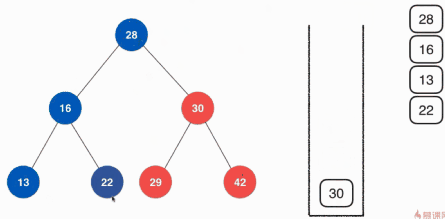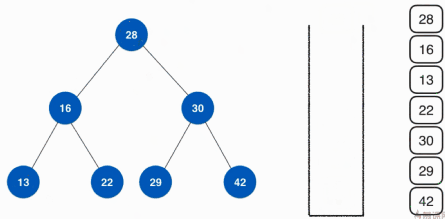
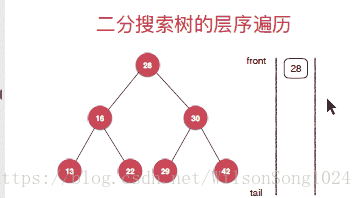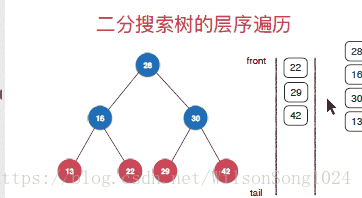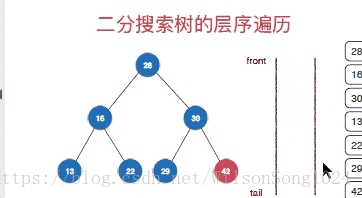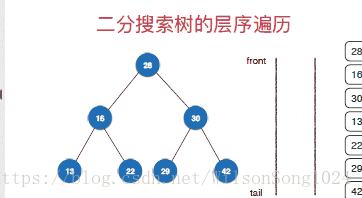
}广度优先遍历(层序遍历)
层序遍历的实现从根节点开,一次安深度往下遍历,按照先左孩子然后右孩子的方式遍历,这里使用队列的方式来实现层序遍历,具体的实现方式如下:
/**
* 层序遍历
*/
public void levelOrder(){
Queue<Node> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()){
Node cur= queue.remove();
if (cur.left != null){
queue.add(cur.left);
}
if (cur.right != null){
queue.add(cur.right);
}
}
}删除书中的节点
删除树中的最大元素和最小元素
首先是先要找到最大和最小元素,根据二分搜索树的性质我们可以很容易的就找到最大最小的元素
/**
* 查找树中最小元素
* @return
*/
public E minimum(){
if (size == 0){
throw new IllegalArgumentException("BST can not be empty");
}
return minimum(root).e;
}
/**
* 查找树中最小元素的节点
* @param node
* @return
*/
private Node minimum(Node node){
if (node.left == null){
return null;
}
return minimum(node.left);
}
/**
* 查找树中最大元素
* @return
*/
public E maximum(){
if (size == 0){
throw new IllegalArgumentException("BST can not be empty");
}
return maximum(root).e;
}
/**
* 查找树中最大元素的节点
* @param node
* @return
*/
private Node maximum(Node node){
if (node.right == null){
return node;
}
return maximum(node.right);
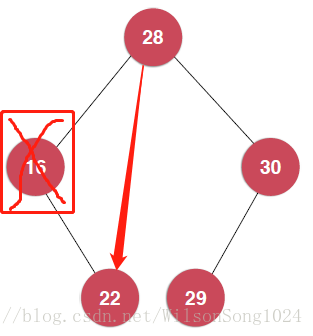
}找到了最大个最小元素之后要将其删除,有需要注意的地方就是当树的结构如下时:
从图上我们可以看出,要是删除的最小元素还有右孩子或者要删除的最大元素还有左孩子的时候,就需要重新把待删除元素的根节点指向其孩子节点。
具体的实现如下:
/**
* 查找树中最小元素
* @return
*/
public E minimum(){
if (size == 0){
throw new IllegalArgumentException("BST can not be empty");
}
return minimum(root).e;
}
/**
* 查找树中最小元素的节点
* @param node
* @return
*/
private Node minimum(Node node){
if (node.left == null){
return null;
}
return minimum(node.left);
}
/**
* 查找树中最大元素
* @return
*/
public E maximum(){
if (size == 0){
throw new IllegalArgumentException("BST can not be empty");
}
return maximum(root).e;
}
/**
* 查找树中最大元素的节点
* @param node
* @return
*/
private Node maximum(Node node){
if (node.right == null){
return node;
}
return maximum(node.right);
}
/**
* 删除最小元素
* @return 返回最小元素的值
*/
public E removeMin(){
E ret = minimum();
root = removeMin(root);
return ret;
}
/**
* 删除最小元素的节点,并返回删除该节点之后新的二分搜索树的根
* @param node 树节点
* @return
*/
public Node removeMin(Node node){
if (node.left == null && node.right != null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
/**
* 删除最大元素,并返回最大元素的值
* @return
*/
public E removeMax(){
E ret = maximum();
root = removeMax(root);
return ret;
}
/**
* 删除最大元素节点并返回删除该节点之后新的二分搜索树的根
* @param node
* @return
*/
private Node removeMax(Node node){
if (node.right == null && node.left != null){
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}删除树中任意节点
删除树中任意的节点需要考虑的问题就多一些了
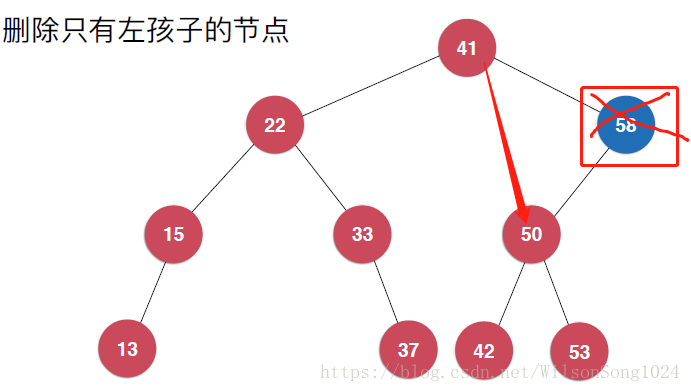
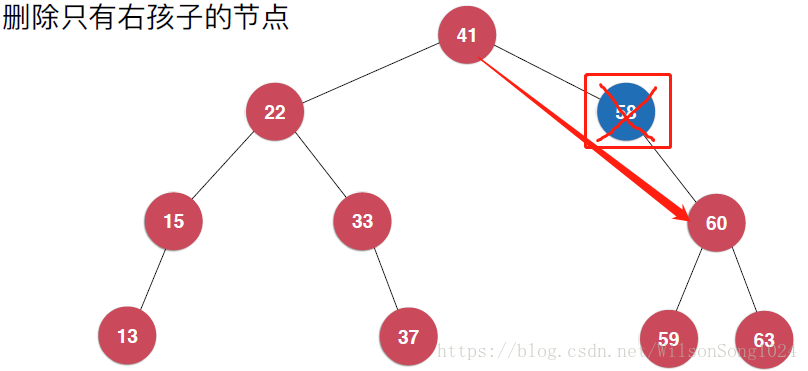
首先删除的节点只有左孩子或者只有右孩子,这个时候其实是比较简单的,删除该节点后,其子节点有其父节点继承即可。如下:
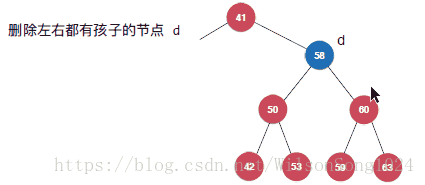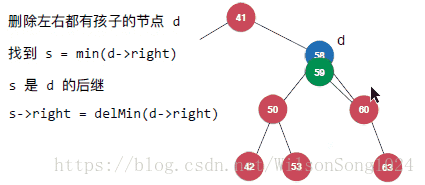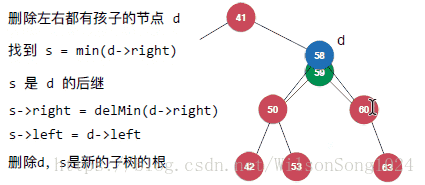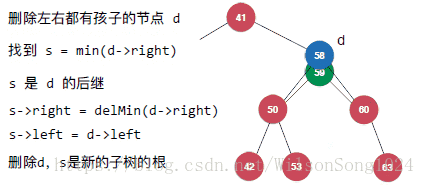
但是当要删除的节点既有左孩子又有右孩子的时候就需要注意了,这里使用Hibbard Deletion方法来实现,具体如下:
其实核心的思想即使找到该节点中右子树中的最小节点来替代该节点成为新的节点。
具体的实现如下:
/**
* 从二分搜索树中删除元素为e的节点
* @param e 删除的元素
* @return
*/
public void remove(E e){
root = remove(root, e);
}
/**
* 删除掉以node为根的二分搜索树中值为e的节点, 递归算法,返回删除节点后新的二分搜索树的根
* @param e 删除的元素
*@param node 节点
* @return
*/
private Node remove(Node node, E e){
if( node == null )
return null;
if( e.compareTo(node.e) < 0 ){
node.left = remove(node.left , e);
return node;
}
else if(e.compareTo(node.e) > 0 ){
node.right = remove(node.right, e);
return node;
}
else{ // e.compareTo(node.e) == 0
// 待删除节点左子树为空的情况
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
// 待删除节点右子树为空的情况
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
// 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}注意
这里删除的操作为什么需要返回删除元素之后的新的树的根节点其实和添加元素的道理是一样的,可以参照一下。一样的理解方式。
这样就完成了树的简单的实现
拓展
当然树还有很多的东西可以去设计,比方说把每个树的节点代表的含义设置的更加丰富
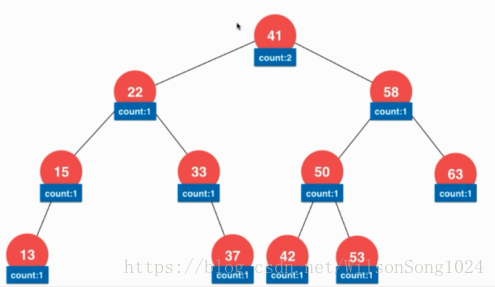
如:树节点除了存值,还存储以其为根节点的树的元素的个数,也就是树的size
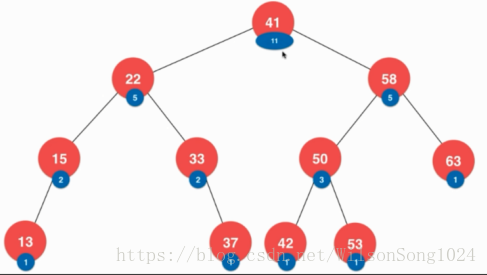
或者是存储该节点在树中的深度
或者是把树设计成可以存储重复的元素,就是在该节点在存一个代表其元素个数的值。
总之树的拓展还有很多,待慢慢探索实现。























 63
63











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








