MATLAB数学建模——时间序列ARIMA及可视化

已于 2024-08-05 17:07:13 修改
阅读量7.7k 收藏 145
点赞数 36
分类专栏： MATLAB数学建模 文章标签： 数学建模 matlab
于 2024-02-25 16:44:38 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/wjw_154378/article/details/136284061
版权

【2024-08-05更新】修正了代码注释和图标的中文格式，增加各选项下结果可视化，Excel表格格式见文末，注意要和代码放在同一文件夹下！ 

完整代码 

首先给出完整代码：

% 运行之前注意保存已有数据
clc; clear;
close all;

% 是否强制确定ARIMA模型（不理想的情况下选择1）
% 值为0时会自动确定模型，但结果可能不理想
isKill = 1;

% 预测时间长度
PreTime = 100;

% 是否进行新时间段的预测，建议先用0再用1
isPre = 1;

% 导入数据集
data = readtable('data.xlsx');
y = data.Value;

% 拆分数据集为训练集和测试集
train_size = floor(0.8 * length(y));
train_data = y(1:train_size);
if isPre == 1
    train_data = y;
end
test_data = y(train_size+1:end);

% 平稳性检验 - ADF检验
[h_adf, p_adf] = adftest(y);
fprintf('ADF检验结果:\n');
fprintf('是否拒绝原假设（序列非平稳）: %d\n', h_adf);
fprintf('p值: %.4f\n', p_adf);

% 平稳性检验 - KPSS检验
[h_kpss, p_kpss] = kpsstest(y);
fprintf('KPSS检验结果:\n');
fprintf('是否拒绝原假设（序列平稳）: %d\n', ~h_kpss);
fprintf('p值: %.4f\n', p_kpss);

% 确定d参数
if isKill == 0
    % 根据ADF和KPSS检验结果确定d参数
    if h_adf == 1 && h_kpss == 0
        d = 0; 
        disp('序列已经平稳')
    elseif h_adf == 0 && h_kpss == 1
        d = 1; 
        disp('序列需要一阶差分')
    elseif h_adf == 1 && h_kpss == 1
        d = 2; 
        disp('序列需要二阶差分')
    else
        error('无法确定d参数');
    end
    
    % 差分处理
    if d > 0
        y_diff = diff(train_data, d);
    else
        y_diff = train_data;
    end
else
    y_diff = train_data;
end

% 确定p和q参数
figure
subplot(2,1,1)
autocorr(y_diff)
title('自相关函数')
xlabel('滞后')
ylabel('自相关系数')
subplot(2,1,2)
parcorr(y_diff)
title('偏自相关函数')
xlabel('滞后')
ylabel('偏自相关系数')

% 训练ARIMA模型
if isKill == 0
    model = arima('D', d, 'ARLags', [1 2], 'MALags', 1); % ARIMA(p, d, q) model
else 
    model = arima(2, 1, 1);
end
model = estimate(model, y_diff);

% 测试未来时间预测情况
if isPre == 0
    horizon = length(y) - train_size;
else
    horizon = PreTime;
end
[forecastTest, YMSE, forecastCI] = forecast(model, horizon, 'Y0', y_diff);
ResultScale(:, 1) = forecastTest - 1.64*sqrt(YMSE); % 90%置信区间下限
ResultScale(:, 2) = forecastTest + 1.64*sqrt(YMSE); % 90%置信区间上限

% 自动确定的可能修正方法
if isKill == 0
    forecastTest = forecastTest + train_data(end) - forecastTest(1);
    ResultScale(:, 1) = forecastTest - 1.64*sqrt(YMSE); % 90%置信区间下限
    ResultScale(:, 2) = forecastTest + 1.64*sqrt(YMSE); % 90%置信区间上限
end

% 可视化预测结果
figure
plot(y, 'ko-')
hold on
if isPre == 0
    % 如果是测试数据预测，绘制测试集部分的预测值和置信区间
    time_axis = (train_size+1:length(y))';
    plot(time_axis, forecastTest, 'b-', 'LineWidth', 1.5)
    plot(time_axis, ResultScale(:, 1), 'r--', 'LineWidth', 1.5)
    plot(time_axis, ResultScale(:, 2), 'r--', 'LineWidth', 1.5)
    fill([time_axis; flipud(time_axis)], [ResultScale(:, 1); flipud(ResultScale(:, 2))], 'r', 'FaceAlpha', 0.3)
else
    % 如果是新时间段预测，绘制新时间段的预测值和置信区间
    time_axis = (length(y)+1:length(y)+PreTime)';
    plot(time_axis, forecastTest, 'b-', 'LineWidth', 1.5)
    plot(time_axis, ResultScale(:, 1), 'r--', 'LineWidth', 1.5)
    plot(time_axis, ResultScale(:, 2), 'r--', 'LineWidth', 1.5)
    fill([time_axis; flipud(time_axis)], [ResultScale(:, 1); flipud(ResultScale(:, 2))], 'r', 'FaceAlpha', 0.3)
end
xlabel('时间')
ylabel('值')
legend('观察值', '预测值', '下置信界限', '上置信界限')
title('ARIMA预测结果及置信区间')

% 误差分析和残差检验（仅当isPre == 0时）
if isPre == 0
    % 误差分析
    error = y(train_size+1:end) - forecastTest;
    mse = mean(error.^2);
    rmse = sqrt(mse);
    mae = mean(abs(error));
    
    fprintf('均方误差 (MSE): %.4f\n', mse);
    fprintf('均方根误差 (RMSE): %.4f\n', rmse);
    fprintf('平均绝对误差 (MAE): %.4f\n', mae);
    
    % 残差检验
    residuals = infer(model, y_diff);
    figure
    subplot(3,1,1)
    plot(residuals)
    xlabel('时间')
    ylabel('残差')
    title('残差')

    % 残差自相关检验
    subplot(3,1,2)
    autocorr(residuals)
    xlabel('滞后')
    ylabel('自相关系数')
    title('残差自相关函数')

    % 残差偏自相关检验
    subplot(3,1,3)
    parcorr(residuals)
    xlabel('滞后')
    ylabel('偏自相关系数')
    title('残差偏自相关函数')
end

代码分段解释

平稳性检验

  • ADF检验：用于检测时间序列是否具有单位根，即是否非平稳。如果拒绝原假设（即h_adf=1），则认为序列平稳。
  • KPSS检验：用于检测时间序列是否平稳。如果拒绝原假设（即h_kpss=0），则认为序列非平稳。
% 平稳性检验 - ADF检验
[h_adf, p_adf] = adftest(y);
fprintf('ADF检验结果:\n');
fprintf('是否拒绝原假设（序列非平稳）: %d\n', h_adf);
fprintf('p值: %.4f\n', p_adf);

% 平稳性检验 - KPSS检验
[h_kpss, p_kpss] = kpsstest(y);
fprintf('KPSS检验结果:\n');
fprintf('是否拒绝原假设（序列平稳）: %d\n', ~h_kpss);
fprintf('p值: %.4f\n', p_kpss);

强制确定模型 

当强制确定模型，即isKill = 1时结果如下图所示：

自动确定模型 

当非强制确定模型时，会给出推荐的差分阶数，如下图所示：

差分（仅非强制确定模型时有效）

根据ADF和KPSS检验结果，确定差分阶数d。如果序列非平稳，则需要进行差分处理以使其平稳。 

% 确定d参数
if isKill == 0
    % 根据ADF和KPSS检验结果确定d参数
    if h_adf == 1 && h_kpss == 0
        d = 0; 
        disp('序列已经平稳')
    elseif h_adf == 0 && h_kpss == 1
        d = 1; 
        disp('序列需要一阶差分')
    elseif h_adf == 1 && h_kpss == 1
        d = 2; 
        disp('序列需要二阶差分')
    else
        error('无法确定d参数');
    end
    
    % 差分处理
    if d > 0
        y_diff = diff(train_data, d);
    else
        y_diff = train_data;
    end
else
    y_diff = train_data;
end

模型选择

通过自相关函数（ACF）和偏自相关函数（PACF）图确定ARIMA模型的p和q参数。这里假设p=2和q=1。

% 确定p和q参数
figure
subplot(2,1,1)
autocorr(y_diff)
title('自相关函数')
xlabel('滞后')
ylabel('自相关系数')
subplot(2,1,2)
parcorr(y_diff)
title('偏自相关函数')
xlabel('滞后')
ylabel('偏自相关系数')

自动确定模型

运行结果如下图所示： 

强制确定模型

运行结果如下图所示： 

模型训练和预测

训练ARIMA模型并进行未来数据的预测，计算预测值的置信区间。

% 训练ARIMA模型
if isKill == 0
    model = arima('D', d, 'ARLags', [1 2], 'MALags', 1); % ARIMA(p, d, q) model
else 
    model = arima(2, 1, 1);
end
model = estimate(model, y_diff);

% 测试未来时间预测情况
if isPre == 0
    horizon = length(y) - train_size;
else
    horizon = PreTime;
end
[forecastTest, YMSE, forecastCI] = forecast(model, horizon, 'Y0', y_diff);
ResultScale(:, 1) = forecastTest - 1.64*sqrt(YMSE); % 90%置信区间下限
ResultScale(:, 2) = forecastTest + 1.64*sqrt(YMSE); % 90%置信区间上限

% 自动确定的可能修正方法
if isKill == 0
    forecastTest = forecastTest + train_data(end) - forecastTest(1);
    ResultScale(:, 1) = forecastTest - 1.64*sqrt(YMSE); % 90%置信区间下限
    ResultScale(:, 2) = forecastTest + 1.64*sqrt(YMSE); % 90%置信区间上限
end

% 可视化预测结果
figure
plot(y, 'ko-')
hold on
if isPre == 0
    % 如果是测试数据预测，绘制测试集部分的预测值和置信区间
    time_axis = (train_size+1:length(y))';
    plot(time_axis, forecastTest, 'b-', 'LineWidth', 1.5)
    plot(time_axis, ResultScale(:, 1), 'r--', 'LineWidth', 1.5)
    plot(time_axis, ResultScale(:, 2), 'r--', 'LineWidth', 1.5)
    fill([time_axis; flipud(time_axis)], [ResultScale(:, 1); flipud(ResultScale(:, 2))], 'r', 'FaceAlpha', 0.3)
else
    % 如果是新时间段预测，绘制新时间段的预测值和置信区间
    time_axis = (length(y)+1:length(y)+PreTime)';
    plot(time_axis, forecastTest, 'b-', 'LineWidth', 1.5)
    plot(time_axis, ResultScale(:, 1), 'r--', 'LineWidth', 1.5)
    plot(time_axis, ResultScale(:, 2), 'r--', 'LineWidth', 1.5)
    fill([time_axis; flipud(time_axis)], [ResultScale(:, 1); flipud(ResultScale(:, 2))], 'r', 'FaceAlpha', 0.3)
end
xlabel('时间')
ylabel('值')
legend('观察值', '预测值', '下置信界限', '上置信界限')
title('ARIMA预测结果及置信区间')

% 误差分析和残差检验（仅当isPre == 0时）
if isPre == 0
    % 误差分析
    error = y(train_size+1:end) - forecastTest;
    mse = mean(error.^2);
    rmse = sqrt(mse);
    mae = mean(abs(error));
    
    fprintf('均方误差 (MSE): %.4f\n', mse);
    fprintf('均方根误差 (RMSE): %.4f\n', rmse);
    fprintf('平均绝对误差 (MAE): %.4f\n', mae);
    
    % 残差检验
    residuals = infer(model, y_diff);
    figure
    subplot(3,1,1)
    plot(residuals)
    xlabel('时间')
    ylabel('残差')
    title('残差')

    % 残差自相关检验
    subplot(3,1,2)
    autocorr(residuals)
    xlabel('滞后')
    ylabel('自相关系数')
    title('残差自相关函数')

    % 残差偏自相关检验
    subplot(3,1,3)
    parcorr(residuals)
    xlabel('滞后')
    ylabel('偏自相关系数')
    title('残差偏自相关函数')
end

自动确定模型

 

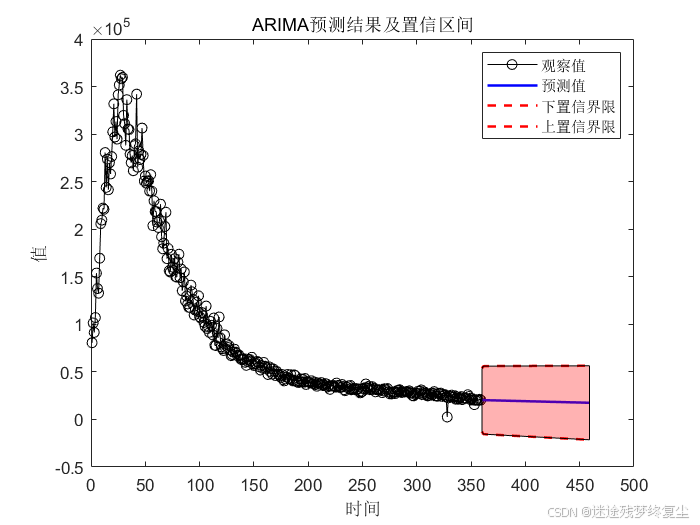
强制确定模型

 

非预测模式 

在非预测模式下，会给出相关参数的检验及可视化结果，如下图所示：

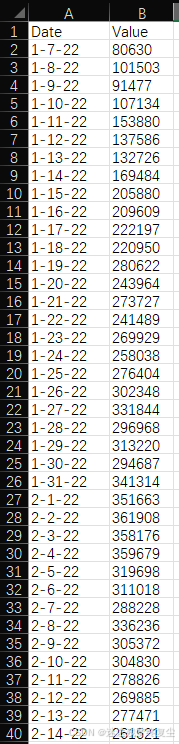
数据表格格式 

【2024-08-05更新】数据表格格式如下：

第68步 时间序列建模实战：ARIMA建模（Matlab）
Jet4505的博客
09-09 5098
第68步 时间序列建模实战：ARIMA建模（Matlab）
时间序列分析matlab_ARIMA时间序列分析入门介绍
weixin_39778447的博客
11-27 4948
ARIMA建模分析分析的步骤数据可视化，识别平稳性对非平稳的时间序列数据，做平稳性处理，得到平稳序列根据偏自相关系数和自相关系数选择模型模型的阶数在确定之后，对模型进行参数估计判断（诊断）残差序列是否为白噪声序列，删除不显著的参数利用已通过检验的模型进行预测预测结果需要通过相关逆变换进行还原时间序列的分解时间序列是由四种因素组成的：长期趋势、季节变动、循环变动、随机波动。当我们对一个时间序列进行预...
时间序列预测中特征构建
思过留痕
07-30 6438
传统统计学习方法： naive approach, moving average, Holt linear, exponential smoothing, ARIMA, and Prophet 现代机器学习方法： 树模型等 深度学习方法： LSTM、Seq2seq、Transform-XL等 树模型需要人为构建特征，同时预测值不可超越区间内取值的上限。 深度学习网络，可以发现输入数据之间的交互关系，同时可以发现趋势。 根据数据可以尝试不同的方法，选择较优的方法。下面是树模型的构造特征的方法。 1. 时间戳特
【监督学习】ARIMA预测模型步骤及matlab实现
最新发布
smile_007996的博客
02-24 1997
本文详细介绍了ARIMA模型以及实现方法！！！
MATLAB_时间序列模型
08-31
MATLAB_时间序列模型共有67页，较为祥细地介绍了时间序列各类模型，并用matlab语言对诸多实例进行建模、预测演示，是一非常好的资料，对时间序列工作者具有较好的指导作用。
【Matlab】时间序列模型(ARIMA)
m0_65032457的博客
08-27 4866
接上一篇博客，用 Matlab 完成代码编写。【学习笔记】时间序列模型(ARIMA)
ARIMA时间序列预测的matlab实现
05-16
在matlab中实现ARIMA时间序列预测。函数形式如下： function [result] = ARIMA_algorithm(data, Periodicity, ACF_P, PACF_Q, n) 其中data为预测所用的数据，为一维列向量；Periodicity为数据的周期；ACF_P和PACF_Q分别是p值和q值；n为想要预测的数据的个数。所返回的结果result是预测出来的数据（一维列向量），同时会画出预测数据的折线图。
ARIMA模型-matlab代码
01-25
ARIMA模型-matlab代码，可以根据自己的实际情况进行参数调节，实现所需要的效果。
基于MATLAB的时间序列分析（建模、预测）
03-03
基于MATLAB，用神经网络对已有数据进行时间序列分析、建模、预测。内含视频教学，有数据可供练习。（教程缺乏预测部分，但是网上有简单的教学，一查就可以查到）主要可用于数学建模，美赛国赛均可。
ARIMA时间序列预测MATLAB代码模板（无需调试）
热门推荐
m0_62526778的博客
02-11 5万+
ARIMA时间序列预测MATLAB代码，通用性强，无需调试
MATLAB数学建模经典案例实战教学PPT (1)_matlab_Matlab数学建模教程_matlab教程_数学建模_
09-28
MATLAB是一种强大的编程环境，专为数值计算、符号计算、数据可视化和图形用户界面构建而设计，广泛应用于工程、科学和数学领域。本教程“MATLAB数学建模经典案例实战教学PPT”针对工科学生和研究人员，旨在通过一...
MATLAB在时间序列建模预测及程序代码
03-04
时间序列是按时间顺序排列的、随时间变化且相互关联的数据序列。分析时间序列的方法构成数据分析的一个重要领域，即时间序列分析。代码
ARIMA模型的MATLAB实现
05-03
此压缩包中包括2018年华为软赛初赛练习数据，数据预处理及应用MATLAB自带的ARIMA函数进行算法可行性验证。
时间序列分析的一些模型Matlab源码
02-17
arima 的一些Matlab源码共享，欢迎下载，相互交流和学习
MATLAB在时间序列建模预测及程序代码（百度文库 第二十四章 时间序列模型）
06-14
时间序列是按时间顺序排列的、随时间变化且相互关联的数据序列。分析时间序列的方法构成数据分析的一个重要领域，即时间序列分析。代码（百度文库 第二十四章 时间序列模型）
时间序列预测建模，ARIMA模型的MATLAB程序实现代码 （含详细讲解）
04-14
MATLAB还提供了`plot`函数，可以帮助我们可视化ARIMA模型的残差，以确认模型是否充分捕捉了时间序列的结构。如果残差显示无明显模式，那么我们可以认为模型已经较好地拟合了数据。 总的来说，ARIMA模型在MATLAB中的...
arima.rar_ARIMA时间序列_arima状态空间_matlab-arima_时间序列 ARIMA_状态空间
09-14
ARIMA模型，全称为自回归整合滑动平均模型（AutoRegressive Integrated Moving Average Model），是时间序列分析中的一种重要工具，常用于预测和建模非平稳时间序列数据。本资料包“arima.rar”主要围绕ARIMA模型在...
MATLAB在时间序列建模预测及程序代码.zip_arima_matlab_时间序列_时间序列 matlab_时间序列预测
09-21
资料包中包含的"MATLAB在时间序列建模预测及程序代码.pdf"很可能是对上述过程的详细解释，包括如何导入数据、构建模型、进行预测以及可视化结果。PDF文档可能会包含具体的MATLAB代码示例，演示如何使用MATLAB的函数...
ARIMA模型预测matlab代码
01-14
### ARIMA Model Prediction Code Example in MATLAB For implementing an ARIMA model and performing predictions using MATLAB, the following code provides a comprehensive guide on how to achieve this. The process involves loading data, fitting an ARIMA model, diagnosing the fit, forecasting future values, and visualizing results. ```matlab % Load your time series data into variable 'y' load('your_time_series_data.mat'); % Replace with actual file or use another method to load data % Plot the original time series data figure; plot(y); title('Original Time Series Data'); xlabel('Time Index'); ylabel('Value'); % Define the ARIMA model parameters (p,d,q) Mdl = arima(2,1,2); % This creates an ARIMA(2,1,2) model as an example; adjust p,d,q based on analysis % Fit the defined ARIMA model to the loaded dataset EstMdl = estimate(Mdl,y); % Generate forecasts over a specified horizon h periods ahead h = 10; % Forecasting horizon can be adjusted according to needs [YF,YMSE] = forecast(EstMdl,h,'Y0',y); % Display predicted means along with confidence intervals disp([YF YMSE]); % Visualize both historical observations alongside forecasts including confidence bounds ub = YF + 1.96*sqrt(YMSE); lb = YF - 1.96*sqrt(YMSE); figure; hold on; plot(y,'Color',[.7,.7,.7]); plot(length(y)+1:h+length(y),YF,'r','LineWidth',2); fill([length(y)+1:h+length(y) fliplr(length(y)+1:h+length(y))], ... [ub fliplr(lb)],'k',... 'EdgeColor','none',... 'FaceAlpha',0.1,... 'HandleVisibility','off'); legend('Observed','Forecasted Mean','Confidence Interval') title(['ARIMA Forecasts Over Next ', num2str(h),' Periods']); xlabel('Time Index'); ylabel('Value'); hold off; ``` This script covers essential steps from defining an appropriate ARIMA(p,d,q) structure through estimation of its coefficients given observed data points up until generating out-of-sample projections while providing uncertainty measures around these estimates via confidence bands[^1].
评论 9
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值