【多样化的思想】反随机测试

随机测试只能在一定程度上实现用例的多样性，因为随机测试仅仅依据统计意义上的“均匀分布”选择每一个测试用例，没有考虑用例之间的关系。那不同的用例之间，到底有着什么样的关系呢？在测试输入空间里，用例之间的关系主要体现为“距离”的远近。

假定测试输入空间有k个维度，对应着k个影响因素。任意两个测试输入点x和y，都可以表示为如下向量形式（其中，xi、yi指的是第i个影响因素的水平）：

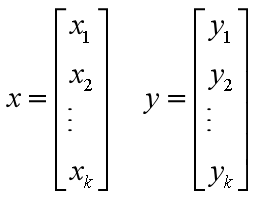
有几种方式可以定义x和y之间的距离。最直观的是欧几里得距离，也就是两点之间连线的长度：

曼哈顿距离，也叫出租车距离。因为像纽约曼哈顿这种地方，街区道路横平竖直，出租车从一点到达另一点的距离，就是南北方向移动的距离加上东西方向移动的距离：

如果我们不考虑移动的具体距离是多少，只考虑南北方向或者东西方向需不需要移动，那么曼哈顿距离就简化成了汉明距离。汉明距离只关心两个测试输入点有多少因素处于不同的水平。比方说，如下两个二进制串，汉明距离是2：

如果测试输入点是自由文本形式的字符串，可以用莱文斯坦距离。两个字符串x、y之间的莱文斯坦距离，是“将x更改为y所需的最少编辑操作次数”。所谓“编辑操作”，指的是单个字符的替换、插入或删除。比如，要把“arcfox”改成“partox”，拢共分3步：第一步：最前边插入一个p；第二步，把c替换成t；第三步：删除f。所以，这两个字符串之间的莱文斯坦距离就是3：

无论采用哪一种距离的定义，测试输入点之间距离越大，都意味着它们之间的差异越大。差异越大，用例的多样性就越强。因此，真正贯彻多样化思想的测试设计方法，一般都会关注测试输入点之间的距离。

反随机测试就是其中的一种。为什么叫“反随机测试”？因为随机测试不管用例之间的关系，反随机测试所反对的，就是这一点。

我们通过一个例子来看一下反随机测试的做法。假定被测对象期望的影响因素是3个二进制变量，测试输入空间里一共有8个点，我们只能选出4个作为测试用例。怎么选呢？

  ① 首先，从测试输入空间中随机选取第一个测试用例，比如000，把它加入测试集：

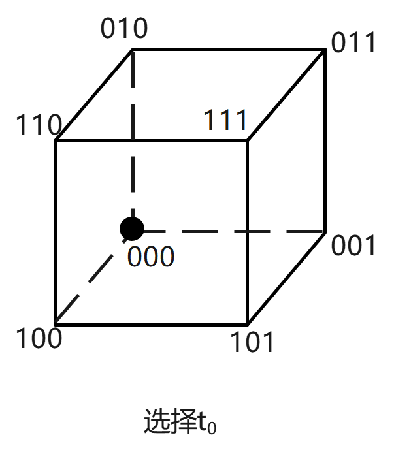
  ② 然后，从剩下的测试输入点中，选择与000距离最大的一个加入测试集，也就是111。如果采用汉明距离，111和000的距离是3：

  ③ 接着，选择与000和111距离之和最大的点加入测试集。剩下的点与000和111距离之和都是3，所以随机选择一个，比如110：

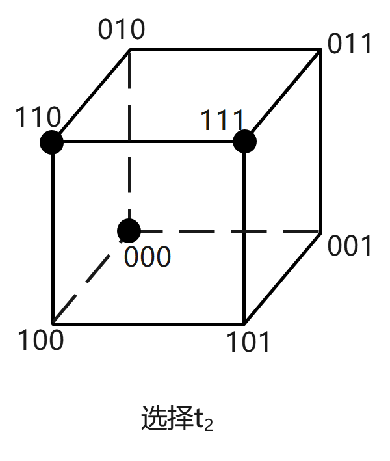
  ④ 最后，选择与000/111/110距离之和最大的点加入测试集，也就是001：

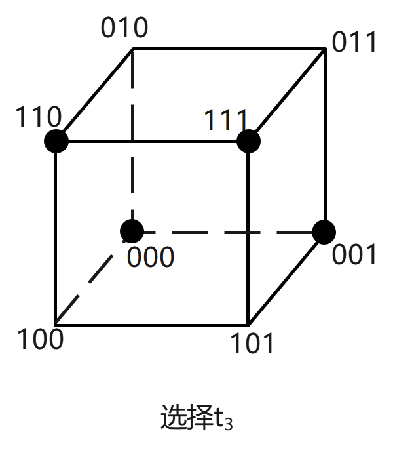
这样，测试选择就完成了。可以看到，反随机测试的思路，是在选择每一个用例的时候，都力求让用例之间的距离之和最大，以此来保证用例的多样性，避免出现用例扎堆的情况。