【机器学习实战】线性支持向量机Python实现

最新推荐文章于 2025-02-10 09:41:29 发布
最新推荐文章于 2025-02-10 09:41:29 发布
阅读量2.5k 收藏 41
点赞数 12
分类专栏： 机器学习 Python 文章标签： 机器学习 支持向量机 python
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/wl1780852311/article/details/121734120
版权
本文深入浅出地介绍了支持向量机的基本概念，从逻辑回归出发，详细推导了SVM的工作原理，包括线性可分情况下的最大化间隔，以及非线性数据的核技巧处理。并通过SMO算法展示了SVM的优化过程，涉及拉格朗日乘子法、KKT条件及对偶问题求解。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

在这里插入图片描述

文章目录

支持向量机

由于理解支持向量机（Support Vector Machines，SVM）需要掌握一些理论知识，而这对读者来说有一定难度，于是建议读者直接下载LIBSVM使用。

好，SVM讲解完毕，完结撒花！！！

开个玩笑（2333)，下面来让我们进入SVM的详细数学推导

前言

什么是SVM？

在机器学习中，支持向量机 (英语: support vector machine，常简称为SVM，又名支持向量网络) 是在分类与回归分析中分析数据的监督式学习模型与相关的学习算法。给定一组训练实例，每个训练实例被标记为属于两个类别中的一个或另一个，SVM训练算法创 建一个将新的实例分配给两个类别之一的模型，使其成为非概率二元线性分类器。SVM模型是将实例表示为空间中的点，这样映射就使得单独类别的实例被尽可能宽的明显的间隔分开。然后，将新的实例映射到同一空间，并基于它们落在间隔的哪一侧来预测所属类别。
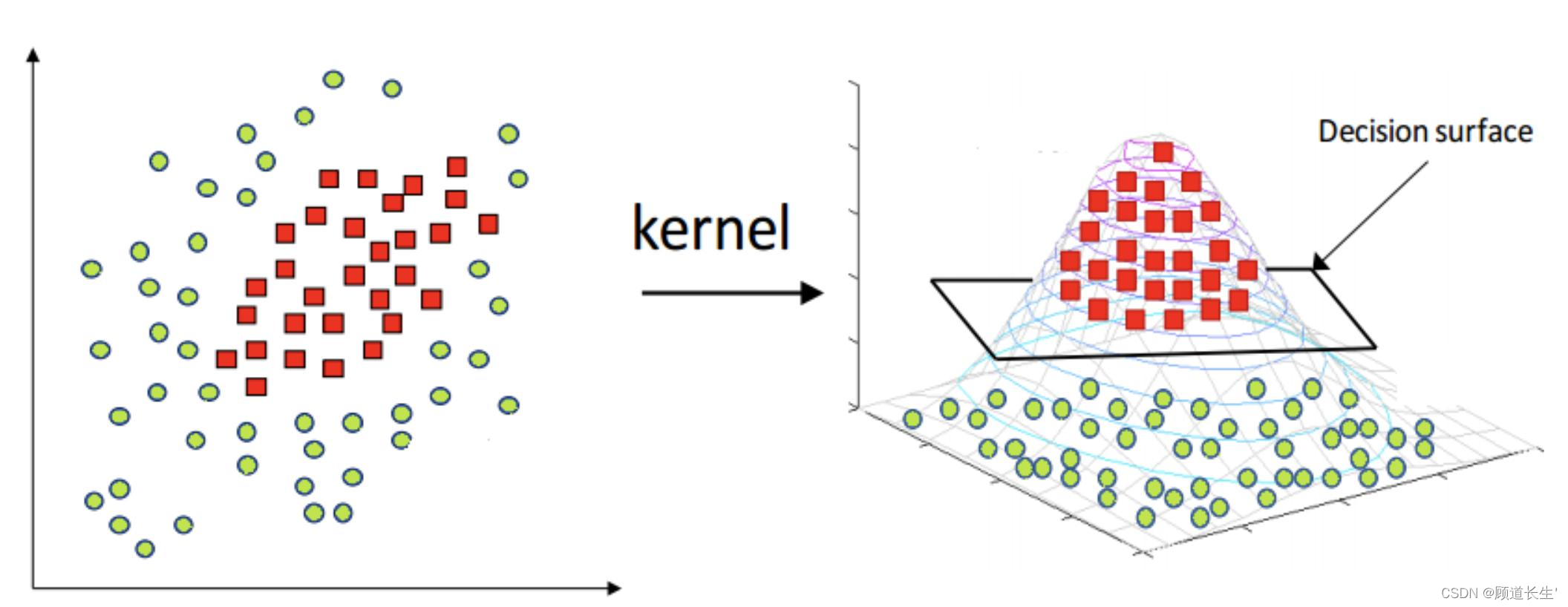
除了进行线性分类之外，SVM还可以使用所谓的核技巧有效地进行非线性分类，将其输入隐式映射到高维特征空间中。
当数据末被标记时，不能进行监督式学习，需要用非监督式学习，它会尝试找出数据到簇的自然聚类，并将新数据映射到这些已形成的簇。将支持向量机改进的聚类算法被称为支持向量聚类，当数据末被标记或者仅一些数据被标记时，支持向量聚类经常在工业应用中用作分类步骤的预处理。

从逻辑回归引出SVM

回顾Logistic回归

Logistic 回归目的是从特征学习出一个 0/1 分类模型, 而这个模型是将特性的线性组合 作为自变量, 由于自变量的取值范围是负无穷到正无穷。因此, 使用 logistic 函数（或称作 sigmoid 函数) 将自变量映射到 ( 0 , 1 ) (0,1) (0,1) 上, 映射后的值被认为是属于 y = 1 y=1 y=1 的概率。

形式化表示就是假设函数

h θ ( x ) = g ( θ T x ) = 1 1 + e − θ T x , h_{\theta}(x)=g\left(\theta^{T} x\right)=\frac{1}{1+e^{-\theta^{T} x}}, hθ​(x)=g(θTx)=1+e−θTx1​,

其中 x \mathrm{x} x 是 n \mathrm{n} n 维特征向量, 函数 g \mathrm{g} g 就是 logistic 函数。

g ( z ) = 1 1 + e − z  的图像是  g(z)=\frac{1}{1+e^{-z}} \text { 的图像是 } g(z)=1+e−z1​ 的图像是 

image.png

可以看到，将无穷映射到了 ( 0 , 1 ) (0,1) (0,1) 。

而假设函数就是特征属于 y = 1 \mathrm{y}=1 y=1 的概率。

P ( y = 1 ∣ x ; θ ) = h θ ( x ) P ( y = 0 ∣ x ; θ ) = 1 − h θ ( x ) \begin{aligned} &P(y=1 \mid x ; \theta)=h_{\theta}(x) \\ &P(y=0 \mid x ; \theta)=1-h_{\theta}(x) \end{aligned} ​P(y=1∣x;θ)=hθ​(x)P(y=0∣x;θ)=1−hθ​(x)​

当我们要判别一个新来的特征属于哪个类时, 只需求 h θ ( x ) h_{\theta}(\mathrm{x}) hθ​(x), 若大于 0.5 0.5 0.5 就是 y = 1 \mathrm{y}=1 y=1 的类, 反之属于 y = 0 y=0 y=0 类。

再审视一下 h θ ( x ) h_{\theta}(\mathrm{x}) hθ​(x), 发现 h θ ( x ) h_{\theta}(\mathrm{x}) hθ​(x) 只和 θ T x \theta^{T} x θTx 有关, θ T x > 0 \theta^{T} x>0 θTx>0, 那么 h θ ( x ) > 0.5 ,   g ( z ) h_{\theta}(\mathrm{x})>0.5, \mathrm{~g}(\mathrm{z}) hθ​(x)>0.5, g(z) 只不过是用来映射, 真实的类别决定权还在 θ T x \theta^{T} x θTx 。还有当 θ T x ≫ 0 \theta^{T} x \gg 0 θTx≫0 时, h θ ( x ) = 1 h_{\theta}(\mathrm{x})=1 hθ​(x)=1, 反之 h θ ( x ) = 0 h_{\theta}(\mathrm{x})=0 hθ​(x)=0 。

如果我们只从 θ T x \theta^{T} x θTx 出发, 希望模型达到的目标无非就是让训练数据中 y = 1 \mathrm{y}=1 y=1 的特征 θ T x ≫ 0 \theta^{T} x \gg 0 θTx≫0, 而是 y = 0 \mathrm{y}=0 y=0 的特征 θ T x ≪ 0 \theta^{T} x \ll 0 θTx≪0 。 Logistic 回归就是要学习得到 θ \theta θ, 使得正例的特征远大于 0 , 负例的特征远 小于 0 , 强调在全部训练实例上达到这个目标。

图形化表示如下:

image.png

中间那条线是 θ T x = 0 \theta^{T} x=0 θTx=0, logistic 回顾强调所有点尽可能地远离中间那条线。学习出的结果也就中间那条线。

考虑上面 3 个点 A 、 B A 、 B A、B 和 C C C 。从图中我们可以确定 A A A 是 × \times × 类别的, 然而C我们是不太确定的, B 还算能够确定。这样我们可以得出结论, 我们更应该关心靠近中间 分割线的点, 让他们尽可能地远离中间线, 而不是在所有点上达到最优。因为那样的话, 要使得一部分点靠近中间线来换取另外一部分点更加远离中间线。我想这就是支持向量机的思路和 logistic 回归的不同点, 一个考虑局部 (不关心已经确定远离的点)（支持向量机）, 一个考虑全局（已经远离的点可能通过调整中间线使其能够更加远离)（逻辑回归）。

SVM形式化表示

我们这次使用的结果标签是 y = − 1 , y = 1 y=-1, y=1 y=−1,y=1, 替换在 logistic 回归中使用的 y = 0 y=0 y=0 和 y = 1 y=1 y=1 。同时将 θ \theta θ 替换成 w w w 和 b b b 。以前的 θ T x = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n \theta^{T} x=\theta_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}+\cdots+\theta_{n} x_{n} θTx=θ0​+θ1​x1​+θ2​x2​+⋯+θn​xn​, 其中认为 x 0 = 1 \mathrm{x}_{0}=1 x0​=1 。现在我们替 换 θ 0 \theta_{0} θ0​ 为 b \mathrm{b} b, 后面替换 θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n \theta_{1} x_{1}+\theta_{2} x_{2}+\cdots+\theta_{n} x_{n} θ1​x1​+θ2​x2​+⋯+θn​xn​ 为 w 1 x 1 + w 2 x 2 + ⋯ + w n x n \mathrm{w}_{1} x_{1}+\mathrm{w}_{2} x_{2}+\cdots+\mathrm{w}_{n} x_{n} w1​x1​+w2​x2​+⋯+wn​xn​ (即 w T x w^{T} x wTx )。这样, 我们让 θ T x = w T x + b \theta^{T} x=w^{T} x+\mathrm{b} θTx=wTx+b, 进一步 h θ ( x ) = g ( θ T x ) = g ( w T x + b ) h_{\theta}(\mathrm{x})=g\left(\theta^{T} x\right)=\mathrm{g}\left(w^{T} x+\mathrm{b}\right) hθ​(x)=g(θTx)=g(wTx+b) 。也就是说除了 y \mathrm{y} y 由 y = 0 \mathrm{y}=0 y=0 变为 y = − 1 y=-1 y=−1, 只是标记不同外, 与 logistic 回归的形式化表示没区别。再明确下假设函数

h w , b ( x ) = g ( w T x + b ) h_{w, b}(\mathrm{x})=g\left(w^{T} x+\mathrm{b}\right) hw,b​(x)=g(wTx+b)

只需考虑 θ T x \theta^{T} x θTx 的正负问题, 而不用关心 g ( z ) g(z) g(z), 因此我们这里将 g ( z ) g(z) g(z) 做 一个简化, 将其简单映射到 y = − 1 y=-1 y=−1 和 y = 1 y=1 y=1 上。映射关系如下:

g ( z ) = { 1 , z ≥ 0 − 1 , z < 0 g(z)=\left\{\begin{aligned} 1, & z \geq 0 \\ -1, & z<0 \end{aligned}\right. g(z)={1,−1,​z≥0z<0​

接下来，先让我们看一下SVM的直观理解

SVM直观解释

以下面这个故事来理解SVM

在很久以前的情人节，大侠要去救他的爱人，但魔鬼和他玩了一个游戏。

魔鬼在桌子上似乎有规律放了两种颜色的球，说：“你用一根棍分开它们？要求：尽量在放更多球之后，仍然适用。”

image.png

于是大侠这样放，干的不错

image.png

然后魔鬼，又在桌上放了更多的球，似乎有一个球站错了阵营。

image.png

SVM就是试图把棍放在最佳位置，好让在棍的两边有尽可能大的间隙。

image.png

现在即使魔鬼放了更多的球，棍仍然是一个好的分界线。

image.png

然后，在SVM工具箱中有另一个更加重要的 trick 。 魔鬼看到大侠已经学会了一个trick，于是魔鬼给了大侠一个新的挑战。

image.png

现在，大侠没有棍可以很好帮他分开两种球了，现在怎么办呢？当然像所有武侠片中一样大侠桌子一拍，球飞到空中。然后，凭借大侠的轻功，大侠抓起一张纸，插到了两种球的中间。

image.png

现在，从魔鬼的角度看这些球，这些球看起来像是被一条曲线分开了

image.png

再之后，无聊的大人们，把这些球叫做 「data」 ，把棍子叫做 「classifier」 , 最大间隙trick 叫做 「optimization」 ， 拍桌子叫做 「kernelling」 , 那张纸叫做 「hyperplane」

线性SVM

先看下线性可分的二分类问题。

image.png

上图中的(a)是已有的数据，红色和蓝色分别代表两个不同的类别。数据显然是线性可分的，但是将两类数据点分开的直线显然不止一条。上图的(b)和©分别给出了B、C两种不同的分类方案，其中黑色实线为分界线，术语称为“决策面”。每个决策面对应了一个线性分类器。虽然从分类结果上看，分类器A和分类器B的效果是相同的。但是他们的性能是有差距的，看下图：

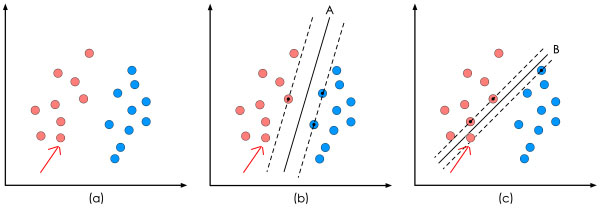
image.png

在"决策面"不变的情况下，又添加了一个红点。可以看到，分类器(b)依然能很好的分类结果，而分类器©则出现了分类错误。显然分类器B的"决策面"放置的位置优于分类器©的"决策面"放置的位置，SVM算法也是这么认为的，它的依据就是分类器B的分类间隔比分类器©的分类间隔大。这里涉及到第一个SVM独有的概念"分类间隔"。在保证决策面方向不变且不会出现错分样本的情况下移动决策面，会在原来的决策面两侧找到两个极限位置（越过该位置就会产生错分现象），如虚线所示。虚线的位置由决策面的方向和距离原决策面最近的几个样本的位置决定。而这两条平行虚线正中间的分界线就是在保持当前决策面方向不变的前提下的最优决策面。两条虚线之间的垂直距离就是这个最优决策面对应的分类间隔（几何间隔）。显然每一个可能把数据集正确分开的方向都有一个最优决策面（有些方向无论如何移动决策面的位置也不可能将两类样本完全分开），而不同方向的最优决策面的分类间隔通常是不同的，那个具有“最大间隔”的决策面就是SVM要寻找的最优解。而这个真正的最优解对应的两侧虚线所穿过的样本点，就是SVM中的支持样本点，称为"支持向量"。

建模

求解这个"决策面"的过程，就是最优化。一个最优化问题通常有两个基本的因素：

  1. 目标函数，也就是你希望什么东西的什么指标达到最好；
  2. 优化对象，你期望通过改变哪些因素来使你的目标函数达到最优。

在线性SVM算法中，目标函数显然就是那个"分类间隔"，而优化对象则是决策面。所以要对SVM问题进行数学建模，首先要对上述两个对象（“分类间隔"和"决策面”）进行数学描述。按照一般的思维习惯，我们先描述决策面。

数学建模的时候，先在二维空间建模，然后再推广到多维。

决策面方程

二维空间下一条直线的方式如下所示:

y = 2 x + b y=2 x+b y=2x+b

现在做个小小的改变，让原来的x轴变成x1，y轴变成 x 2 x 2 x2 。

x 2 = a x 1 + b x_{2}=a x_{1}+b x2​=ax1​+b

移项得:

a x 1 − x 2 + b = 0 \mathrm{ax}_{1}-\mathrm{x}_{2}+\mathrm{b}=0 ax1​−x2​+b=0

将公式向量化得:

[ a − 1 ] [ X 1 X 2 ] + b = 0 [a-1]\left[\begin{array}{l} {X}_{1} \\ {X}_{2} \end{array}\right]+b=0 [a−1][X1​X2​​]+b=0

进一步向量化，用 w w w列向量和 x x x列向量和标量 γ \gamma γ 进一步向量化:

ω T x + γ = 0 \omega^{T} x+\gamma=0 ωTx+γ=0

其中，向量 w w w 和 x x x 分别为:

ω = [ ω 1 , ω 2 , ⋯   , ω n ] T x = [ x 1 , x 2 , ⋯   , x n ] T \begin{aligned} &\omega=\left[\omega_{1}, \omega_{2}, \cdots, \omega_{n}\right]^{T} \\ &\boldsymbol{x}=\left[x_{1}, x_{2}, \cdots, x_{n}\right]^{T} \end{aligned} ​ω=[ω1​,ω2​,⋯,ωn​]Tx=[x1​,x2​,⋯,xn​]T​

那么向量化后的直线，现在成为了超平面，而超平面的 w w w和 γ \gamma γ的几何意义是什么呢?

γ \gamma γ还是代表直线的截距。而 w w w则是超平面的法向量。

详细证明： w w w是直线的法向量

微信图片_20211203101247.jpg

至此，顺利推出决策面方程，之后统称为超平面方程

分类间隔方程

对于一个二维平面的简单例子进行推导

image.png

已经知道间隔（margin)的大小实际上就是支持向量对应的样本点到决策面的距离的二倍。那么图中的距离d怎么求? 高中都学过，点到直线的距离距离公式如下:

d = ∣ A x 0 + B y 0 + C A 2 + B 2 ∣ d=\left|\frac{A x_{0}+B y_{0}+C}{\sqrt{A^{2}+B^{2}}}\right| d=∣∣∣∣​A2+B2 ​Ax0​+By0​+C​∣∣∣∣​

公式中的直线方程为 A x 0 + B y 0 + C = 0 A x_0+B y_0+C=0 Ax0​+By0​+C=0 ，点 P P P 的坐标为 ( x 0 , y 0 ) (x_0, y_0) (x0​,y0​) 。
现在，将直线方程扩展到多维，用求得的超平面方程，对公式进行如下变形:

d = ∣ ω T x + γ ∣ ∣ ∣ ω ∣ ∣ d=\frac{\left|\omega^{T} x+\gamma\right|}{|| \omega||} d=∣∣ω∣∣∣∣​ωTx+γ∣∣​​

此乃几何间隔

这个 d就是"分类间隔"。其中 ∥ w ∥ \|w\| ∥w∥ 表示w的二范数，求所有元素的平方和，然后再开方。比如对于二维平面:

ω = [ ω 1 , ω 2 ] T \omega=\left[\omega_{1}, \omega_{2}\right]^{T} ω=[ω1​,ω2​]T

那么

∥ ω ∥ = ω 1 2 + ω 2 2 \|\omega\|=\sqrt[]{\omega_{1}^{2}+\omega_{2}^{2}} ∥ω∥=ω12​+ω22​ ​

SVM的目的是为了找出一个分类效果好的超平面作为分类器。分类器的好坏的评定依据是分类间隔 W = 2 d W=2 d W=2d 的大小，即分类间隔 W W W越大，认为这个超平面的分类效果越好。此时，求解超平面的问题就变成了求解分类间隔W最大化的为题。W的最大化也就是 d \mathrm{d} d 最大化。

函数间隔和几何间隔解释：

给定一个训练样本 ( x ( i ) , y ( i ) ) , x \left(x^{(i)}, y^{(i)}\right), \mathrm{x} (x(i),y(i)),x 是特征, y \mathrm{y} y 是结果标签。 i \mathrm{i} i 表示第 i \mathrm{i} i 个样本。我们定义函数间隔如下:

γ ^ ( i ) = y ( i ) ( w T x ( i ) + b ) \hat{\gamma}^{(\mathrm{i})}=y^{(i)}\left(w^{T} x^{(i)}+b\right) γ^​(i)=y(i)(wTx(i)+b)

可想而知, 当 y ( i ) = 1 y^{(i)}=1 y(i)=1 时, 在我们的 g ( z ) \mathrm{g}(\mathrm{z}) g(z) 定义中, w T x ( i ) + b ≥ 0 , γ ^ ( i ) w^{T} x^{(i)}+b \geq 0, \hat{\gamma}^{(\mathrm{i})} wTx(i)+b≥0,γ^​(i) 的值实际上就是 ∣ w T x ( i ) + b ∣ \left|w^{T} x^{(i)}+b\right| ∣∣​wTx(i)+b∣∣​ 。反之亦然。为了使函数间隔最大 (更大的信心确定该例是正例还是反例), 当 y ( i ) = 1 y^{(i)}=1 y(i)=1 时, w T x ( i ) + b w^{T} x^{(i)}+b wTx(i)+b 应该是个大正数, 反之是个大负数。因此函数间隔代表了我们认为特 征是正例还是反例的确信度。
继续考虑 w \mathrm{w} w 和 b \mathrm{b} b, 如果同时加大 w \mathrm{w} w 和 b \mathrm{b} b, 比如在 ( w T x ( i ) + b ) \left(w^{T} x^{(i)}+b\right) (wTx(i)+b) 前面乘个系数比如 2 , 那 么所有点的函数问隔都会增大二倍, 这个对求解问题来说不应该有影响, 因为我们要求解的 是 w T x + b = 0 w^{T} x+b=0 wTx+b=0, 同时扩大 w w w 和 b b b 对结果是无影响的。这样, 我们为了限制 w w w 和 b b b, 可能需 要加入归一化条件, 毕竟求解的目标是确定唯一一个 w w w 和 b b b, 而不是多组线性相关的向量。 这个归一化一会再考虑。
刚刚我们定义的函数间隔是针对某一个样本的, 现在我们定义全局样本上的函数间隔 γ ^ = min ⁡ i = 1 , … , m γ ^ ( i ) \hat{\gamma}=\min _{i=1, \ldots, m} \hat{\gamma}^{(i)} γ^​=mini=1,…,m​γ^​(i)

说白了就是在训练样本上分类正例和负例确信度最小那个函数间隔。
接下来定义几何间隔, 先看图

image.png

假设我们有了 B \mathrm{B} B 点所在的 w T x + b = 0 w^{T} x+b=0 wTx+b=0 分割面。任何其他一点, 比如 A \mathrm{A} A 到该面的距离以 γ ( i ) \gamma^{(i)} γ(i) 表示, 假设 B \mathrm{B} B 就是 A \mathrm{A} A 在分割面上的投影。我们知道向量 B A \mathrm{BA} BA 的方向是 W \mathrm{W} W (分割面的梯度), 单位向量是 w ∥ w ∥ ∘ \frac{w}{\|w\|^{\circ}} ∥w∥∘w​ A 点是 ( x ( i ) , y ( i ) ) \left(x^{(i)}, y^{(i)}\right) (x(i),y(i)), 所以 B 点是 x = x ( i ) − γ ( i ) w ∥ w ∥ \mathrm{x}=x^{(i)}-\gamma^{(i)} \frac{w}{\|w\|} x=x(i)−γ(i)∥w∥w​ (利用初中的几何知识), 带入 w T x + b = 0 w^{T} x+b=0 wTx+b=0 得,

w T ( x ( i ) − γ ( i ) w ∣ ∣ w ∣ ∣ ) + b = 0 \mathbf{w}^{T}\left(x^{(i)}-\gamma^{(i)} \frac{w}{|| \mathbf{w}||}\right)+b=0 wT(x(i)−γ(i)∣∣w∣∣w​)+b=0

进一步得到

γ ( i ) = w T x ( i ) + b ∥ w ∥ = ( w ∥ w ∥ ) T x ( i ) + b ∥ w ∥ \gamma^{(i)}=\frac{w^{T} x^{(i)}+b}{\|w\|}=\left(\frac{w}{\|w\|}\right)^{T} x^{(i)}+\frac{b}{\|w\|} γ(i)=∥w∥wTx(i)+b​=(∥w∥w​)Tx(i)+∥w∥b​

γ ( i ) \gamma^{(i)} γ(i)实际上就是点到平面距离
再换种更加优雅的写法:

γ ( i ) = y ( i ) ( ( w ∥ w ∥ ) T x ( i ) + b ∥ w ∥ ) \gamma^{(i)}=y^{(i)}\left(\left(\frac{w}{\|w\|}\right)^{T} x^{(i)}+\frac{b}{\|w\|}\right) γ(i)=y(i)((∥w∥w​)Tx(i)+∥w∥b​)

当 || w ∣ ∣ = 1 w||=1 w∣∣=1 时, 不就是函数间隔吗? 是的, 前面提到的函数间隔归一化结果就是几何间隔。他们为什么会一样呢? 因为函数问隔是我们定义的, 在定义的时候就有几何间隔的色彩。

同样, 同时扩大 w w w 和 b , w b, w b,w 扩大几倍, ∥ w ∥ \|w\| ∥w∥ 就扩大几倍, 结果无影响。同样定义全局的几何 间隔 γ = min ⁡ i = 1 , … , m γ ( i ) \gamma=\min _{i=1, \ldots, m} \gamma^{(i)} γ=mini=1,…,m​γ(i).

约束条件

看起来起来，已经顺利获得了目标函数的数学形式。但是为了求解w的最大值。不得不面对如下问题:

  • 如何判断超平面是否将样本点正确分类?
  • 知道要求距离 d \mathrm{d} d 的最大值, 首先需要找到支持向量上的点, 怎么在众多的点中选出支持向量上的点呢?

上述需要面对的问题就是约束条件，也就是说优化的变量 d d d 的取值范围受到了限制和约束。事实上约束条件一直是最优化问题里最让人头疼的东西。但既然已经知道了这些约束条件 确实存在，就得不用数学语言对他们进行描述。但SVM算法通过一些巧妙的小技巧，将这些约束条件融合到一个不等式里面。

这个二维平面上有两种点，分别对它们进行标记:

  • 红新色的圆点标记为 1 ，人为规定其为正样本;
  • 蓝竡色的五角星标记为 − 1 -1 −1 ，人为规定其为负样本。

对每个样本点 x i x_i xi​加上一个类别标签 y i y_i yi​ :

y i = { + 1  红色点  − 1  蓝色点  y_{i}= \begin{cases}+1 & \text { 红色点 } \\ -1 & \text { 蓝色点 }\end{cases} yi​={+1−1​ 红色点  蓝色点 ​

如果超平面方程能够完全正确地对上图的样本点进行分类, 就会满足下面的方程:

{ ω T x i + γ > 0 y i = 1 ω T x i + γ < 0 y i = − 1 \left\{\begin{array}{cc} \omega^{T} x_{i}+\gamma>0 & y_{i}=1 \\ \omega^{T} x_{i}+\gamma<0 & y_{i}=-1 \end{array}\right. {ωTxi​+γ>0ωTxi​+γ<0​yi​=1yi​=−1​

如果要求再高一点，假设决策面正好处于间隔区域的中轴线上，并且相应的支持向量对应的样本点到决策面的距离为 d d d ，那么公式进一步写成:

{ ω T x i + γ ∥ ω ∥ ≥ d ∀ y i = 1 ω T x i + γ ∥ ω ∥ ≤ − d ∀ y i = − 1 \begin{cases}\frac{\omega^{T} x_{i}+\gamma}{\|\omega\|} \geq \mathrm{d} \quad & \forall y_{i}=1 \\ \frac{\omega^{T} x_{i}+\gamma}{\|\omega\|} \leq-\mathrm{d} \quad & \forall y_{i}=-1\end{cases} {∥ω∥ωTxi​+γ​≥d∥ω∥ωTxi​+γ​≤−d​∀yi​=1∀yi​=−1​

上述公式的解释就是，对于所有分类标签为1和-1样本点，它们到直线的距离都大于等于 d d d(支持向量上的样本点到超平面的距离)。公式两边都除以 d d d，就可以得到：

{ ω d T x i + γ d ≥ 1 ∀ y i = 1 ω d T x i + γ d ≤ − 1 ∀ y i = − 1 \left\{\begin{array}{lr} \omega_{d}^{T} x_{i}+\gamma_{d} \geq 1 & \forall y_{i}=1 \\ \omega_{d}^{T} x_{i}+\gamma_{d} \leq-1 & \forall y_{i}=-1 \end{array}\right. {ωdT​xi​+γd​≥1ωdT​xi​+γd​≤−1​∀yi​=1∀yi​=−1​

其中，

ω d = ω ∥ ω ∥ d , γ d = γ ∥ ω ∥ d \boldsymbol{\omega}_{d}=\frac{\boldsymbol{\omega}}{\|\boldsymbol{\omega}\| d}, \gamma_{d}=\frac{\gamma}{\|\boldsymbol{\omega}\| d} ωd​=∥ω∥dω​,γd​=∥ω∥dγ​

因为 ∥ w ∥ \|w\| ∥w∥和 d d d都是标量。所上述公式的两个矢量，依然描述一条直线的法向量和截距。

ω d T x + γ d = 0 ω T x + γ = 0 \begin{aligned} &\omega_{d}^{T} \boldsymbol{x}+\gamma_{d}=0 \\ &\omega^{T} \boldsymbol{x}+\gamma=0 \end{aligned} ​ωdT​x+γd​=0ωTx+γ=0​

上述两个公式，都是描述一条直线，数学模型代表的意义是一样的。现在，对 w d w_d wd​和 y d y_d yd​重新 起个名字, 就叫它们w和 γ \gamma γ。因此, 就可以说: "对于存在分类间隔的两类样本点, 一定可以找到一些超平面，使其对于所有的样本点均满足下面的条件: "

{ ω T x i + γ ≥ 1 ∀ y i = 1 ω T x i + γ ≤ − 1 ∀ y i = − 1 \left\{\begin{array}{lr} \omega^{T} x_{i}+\gamma \geq 1 & \forall y_{i}=1 \\ \omega^{T} x_{i}+\gamma \leq-1 & \forall y_{i}=-1 \end{array}\right. {ωTxi​+γ≥1ωTxi​+γ≤−1​∀yi​=1∀yi​=−1​

上述方程即给出了SVM最优化问题的约束条件。这时侯，可能有人会问了，为什么标记为 1 和- 1 呢? 因为这样标记方便将上述方程变成如下形式:

y i ( ω T x i + γ ) ≥ 1 ∀ x i y_{i}\left(\omega^{T} x_{i}+\gamma\right) \geq 1 \quad \forall x_{i} yi​(ωTxi​+γ)≥1∀xi​

正是因为标签为 1 和 − 1 -1 −1, 才方便将约束条件变成一个约束方程，从而方便计算。

线性SVM优化问题描述

现在整合一下思路，已经得到目标函数:

d = ∣ ω T x + γ ∣ ∥ ω ∥ d=\frac{\left|\omega^{T} x+\gamma\right|}{\|\omega\|} d=∥ω∥∣∣​ωTx+γ∣∣​​

优化目标是 d d d 最大化。用支持向量上的样本点求解d的最大化的问题，那么支持向量上的样本点有什么特点呢?

∣ ω T x i + γ ∣ = 1 ∀  支持向量上的样本点  x i \left|\omega^{T} x_{i}+\gamma\right|=1 \quad \forall \text { 支持向量上的样本点 } x_{i} ∣∣​ωTxi​+γ∣∣​=1∀ 支持向量上的样本点 xi​

现在就可以将目标函数进一步化简:

d = 1 ∥ ω ∥ d=\frac{1}{\|\omega\|} d=∥ω∥1​

因为，只关心支持向量上的点。随后求解 d d d 的最大化问题变成了 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣的最小化问题。进而 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣的最小化问题等效于

min ⁡ 1 2 ∥ ω ∥ 2 \min \frac{1}{2}\|\omega\|^{2} min21​∥ω∥2

为什么要做这样的等效呢? 这是为了在进行最优化的过程中对目标函数求导时比较方便，但这绝对不影响最优化问题最后的求解。

将最终的目标函数和约束条件放在一起进行描述:

min ⁡ 1 2 ∥ ω ∥ 2  s.t.  y i ( ω T x i + b ) ≥ 1 , i = 1 , 2 , … , n \begin{aligned} &\min \frac{1}{2}\|\omega\|^{2} \\ &\text { s.t. } y_{i}\left(\omega^{T} x_{i}+b\right) \geq 1, i=1,2, \ldots, n \end{aligned} ​min21​∥ω∥2 s.t. yi​(ωTxi​+b)≥1,i=1,2,…,n​

这里n是样本点的总个数，缩写s.t.表示"Subject to"，是"服从某某条件"的意思。上述公式描述的 是一个典型的不等式约束条件下的二次型函数优化问题,这属于非线性规划问题，同时也是支持向量机的基本数学模型。

求解凸优化问题知识补充

知识补充-凸优化

凸优化问题

  • 目标函数是凸函数
  • 可行域是凸集
  • 局部最优解=全局最优解

凸集的定义: 对于一个点的集合 C \mathrm{C} C, 有 x , y \mathrm{x}, \mathrm{y} x,y 它都是属于 C 里面的两个点, 它们两点的连线中任何一点也是属于集合 C \mathrm{C} C的，
θ x + ( 1 − θ ) y ∈ C \theta x+(1-\theta) y \in C θx+(1−θ)y∈C
0 ≤ θ ≤ 1 0\le \theta \le 1 0≤θ≤1
image.png

典型的凸集
欧式空间 R n R^{n} Rn
x , y ∈ R n ⇒ θ x + ( 1 − θ ) y ∈ R n x, y \in R^{n} \Rightarrow \theta x+(1-\theta) y \in R^{n} x,y∈Rn⇒θx+(1−θ)y∈Rn
它的意义在于，很多时候可行域就是欧式空间, 那肯定是凸集

凸集的交集还是凸集

仿射函数 f ( x ) f(x) f(x) 称为仿射函数, 如果它满足 f ( x ) = a ⋅ x + b , a ∈ R n , b ∈ R , x ∈ R n f(x)=a \cdot x+b, a \in \mathbf{R}^{n}, b \in \mathbf{R}, x \in \mathbf{R}^{n} f(x)=a⋅x+b,a∈Rn,b∈R,x∈Rn 。

通常我们需要求解的最优化问题有如下几类:

  • (a)无约束优化问题, 可以写为:
    min ⁡ f ( x ) \min f(x) minf(x)
  • (b)有等式约束的优代问题, 可以写为:
    min ⁡ f ( x ) \min f(x) minf(x)
    s.t. h i ( x ) = 0 , i = 1 , 2 , … , n h_{i(x)}=0, \quad i=1,2, \ldots, n hi(x)​=0,i=1,2,…,n
  • ©有不等式约束的优化问题, 可以㝍为:
    min ⁡ f ( x ) \min f(x) minf(x)
    s.t. g i ( x ) ≤ 0 , i = 1 , 2 , … , n g_{i(x)} \leq 0, \quad i=1,2, \ldots, n gi(x)​≤0,i=1,2,…,n
    h j ( x ) = 0 , j = 1 , 2 , … , m h_{j(x)}=0, \quad j=1,2, \ldots, m hj(x)​=0,j=1,2,…,m

对于第 (a)类的优化问题，常常使用的方法就是费马大定理(Fermat)，即使用求取函数 f ( x ) f(x) f(x) 的导数， 然后令其为零，可以求得候选最优值，再在这些候选值中验证; 如果是凸函数，可以保证是最 解。这也就是我们高中经常使用的求函数的极值的方法。
对于第(b)类的优化问题，常常使用的方法就是拉格朗日乘子法 (Lagrange Multiplier)，即把等 式约束 i i ( x ) \mathrm{i} i(\mathrm{x}) ii(x) 用一个系数与 f ( x ) \mathrm{f}(\mathrm{x}) f(x) 写为一个式子，称为拉格朗日函数，而系数称为拉格朗日乘子。通过拉格朗日函数对各个变量求导，令其为零，可以求得候选值集合，然后验证求得最优值。
对于第©类的优化问题，常常使用的方法就是KKT条件。同样地，我们把所有的等式、不等式约束 与 f ( x ) f(x) f(x) 写为一个式子，也叫拉格朗日函数，系数也称拉格朗日乘子，通过一些条件，可以求出最优值的必要条件，这个条件称为KKT条件。
必要条件和充要条件如果不理解，可以看下面这句话:

  • A的必要条件就是A可以推出的结论
  • A的充分条件就是可以推出A的前提
拉格朗日函数

首先，先要从宏观的视野上了解一下拉格朗日对偶问题出现的原因和背景。
要求解的是最小化问题，所以一个直观的想法是如果能够构造一个函数，使得该函数在可行解区域内与原目标函数完全一致，而在可行解区域外的数值非常大，甚至是无穷大，那么 这个没有约束条件的新目标函数的优化问题就与原来有约束条件的原始目标函数的优化问题是等价的问题。这就是使用拉格朗日方程的目的，它将约束条件放到目标函数中，从而将有约束优化问题转换为无约束优化问题。
随后，人们又发现，使用拉格朗日获得的函数，使用求导的方法求解依然困难。进而，需要对问题 再进行一次转换，即使用一个数学技巧：拉格朗日对偶。
所以，显而易见的是，在拉格朗日优化我们的问题这个道路上，需要进行下面二个步骤:

  • 将有约束的原始目标函数转换为无约束的新构造的拉格朗日目标函数
  • 使用拉格朗日对偶性，将不易求解的优化问题转化为易求解的优化

下面，进行第一步: 将有约束的原始目标函数转换为无约束的新构造的拉格朗日目标函数
公式变形如下:

L ( w , b , α ) = 1 2 ∥ w ∥ 2 − ∑ i = 1 n α i ( y i ( w T x i + b ) − 1 ) \mathcal{L}(\boldsymbol{w}, b, \boldsymbol{\alpha})=\frac{1}{2}\|\boldsymbol{w}\|^{2}-\sum_{i=1}^{n} \alpha_{i}\left(y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right)-1\right) L(w,b,α)=21​∥w∥2−i=1∑n​αi​(yi​(wTxi​+b)−1)

其中 α i \alpha_i αi​是拉格朗日乘子， α i \alpha_i αi​大于等于 0 ，是构造新目标函数时引入的系数变量(自己设置)。现在令:

θ ( w ) = max ⁡ α i ≥ 0 L ( w , b , α ) \theta(w)=\max _{\alpha_{i} \geq 0} \mathcal{L}(w, b, \alpha) θ(w)=αi​≥0max​L(w,b,α)

当样本点不满足约束条件时，即在可行解区域外:

y i ( ω T x i + b ) < 1 y_{i}\left(\omega^{T} x_{i}+b\right)<1 yi​(ωTxi​+b)<1

此时，将 α i \alpha_i αi​设置为正无穷，此时 θ ( w ) \theta(\mathrm{w}) θ(w) 显然也是正无穷。
当样本点满足约束条件时，即在可行解区域内:

y i ( ω T x i + b ) ≥ 1 y_{i}\left(\boldsymbol{\omega}^{T} x_{i}+b\right) \geq 1 yi​(ωTxi​+b)≥1

此时，显然 θ ( w ) \theta(w) θ(w) 为原目标函数本身。将上述两种情况结合一下，就得到了新的目标函数：

θ ( ω ) = { 1 2 ∥ ω ∥ 2 + ∞ x ∈  非可行区域  \theta(\omega)=\left\{\begin{array}{l} \frac{1}{2}\|\omega\|^{2} \\ +\infty \end{array} \quad x \in\right. \text { 非可行区域 } θ(ω)={21​∥ω∥2+∞​x∈ 非可行区域 

此时，再看我们的初衷，就是为了建立一个在可行解区域内与原目标函数相同，在可行解区域外函数值趋近于无穷大的新函数，现在做到了。
现在，问题变成了求新目标函数的最小值，即:

min ⁡ w , b θ ( w ) = min ⁡ w , b max ⁡ α i ≥ 0 L ( w , b , α ) = p ∗ \min _{w, b} \theta(w)=\min _{w, b} \max _{\alpha_{i} \geq 0} \mathcal{L}(w, b, \alpha)=p^{*} w,bmin​θ(w)=w,bmin​αi​≥0max​L(w,b,α)=p∗

这里用 p ∗ p^{*} p∗ 表示这个问题的最优值，且和最初的问题是等价的。

接下来，进行第二步：将不易求解的优化问题转化为易求解的优化
看一下新目标函数，先求最大值，再求最小值。这样的话，首先就要面对带有需要 求解的参数 w w w 和 b b b 的方程，而 α \alpha α 又是不等式约束，这个求解过程不好做。所以，需要使用拉格朗日函数对偶性，将最小和最大的位置交换一下，这样就变成了:

max ⁡ α i ≥ 0 min ⁡ w , b L ( w , b , α ) = d ∗ \max _{\alpha_{i} \geq 0} \min _{w, b} \mathcal{L}(w, b, \alpha)=d^{*} αi​≥0max​w,bmin​L(w,b,α)=d∗

交换以后的新问题是原始问题的对偶问题，这个新问题的最优值用 d ∗ \mathrm{d}^{*} d∗ 来表示。而且 d ∗ < = p ∗ \mathrm{d}^{*}<=\mathrm{p}^{*} d∗<=p∗ 。但其实我们关心的是 d = p d=p d=p 的时候，这才是我们要的解。需要什么条件才能让 d = p d=p d=p 呢?

  • 首先必须满足这个优化问题是凸优化问题。
  • 其次，需要满足KKT条件。
    凸优化问题的定义是: 求取最小值的目标函数为凸函数的一类优化问题。目标函数是凸函数已经知道，这个优化问题又是求最小值。所以这个最优化问题就是凸优化问题。
    接下来，就是探讨是否满足KKT条件了。
KKT条件

已经使用拉格朗日函数对我们的目标函数进行了处理，生成了一个新的目标函数。通过一些条件，可以求出最优值的必要条件，这个条件就是接下来要说的KKT条件。一个最优化模型能够表示成下列标准形式:

min ⁡ f ( x )  s.t.  h j ( x ) = 0 , j = 1 , 2 , ⋯   , p g k ( x ) ≤ 0 , k = 1 , 2 , ⋯   , q x ∈ X ⊂ R n \begin{array}{ll} \min & f(\boldsymbol{x}) \\ \text { s.t. } & h_{j}(\boldsymbol{x})=0, j=1,2, \cdots, p \\ & g_{k}(\boldsymbol{x}) \leq 0, k=1,2, \cdots, q \\ & \boldsymbol{x} \in X \subset \mathbb{R}^{n} \end{array} min s.t. ​f(x)hj​(x)=0,j=1,2,⋯,pgk​(x)≤0,k=1,2,⋯,qx∈X⊂Rn​

KKT条件的全称是Karush-Kuhn-Tucker条件，KKT条件是说最优值条件必须满足以下条件:

  • 条件一: 经过拉格朗日函数处理之后的新目标函数 L ( w , b , α ) L(w, b, \alpha) L(w,b,α) 对 x x x 求导为零:
  • 条件二: h j ( x ) = 0 h_{j}(x)=0 hj​(x)=0;
  • 条件三: α ∗ g k ( k ) = 0 \alpha * g_{k}(k)=0 α∗gk​(k)=0;

等式约束和不等式约束的几何意象(二维空间中）

image.png h j ( x ) = 0 h_j(x)=0 hj​(x)=0，等式约束对应的可行解空间就是一条线

image.png g k ( x ) ≤ 0 g_k(x) \leq 0 gk​(x)≤0,不等式约束对应的则是这条线以及线的某一侧对应的区域

以上x与前面的样本点毫无关系，只是一种通用表示

对于这个的优化问题:
min ⁡ 1 2 ∥ ω ∥ 2 \min \frac{1}{2}\|\omega\|^{2} min21​∥ω∥2
s.t. y i ( ω T x i + b ) ≥ 1 , i = 1 , 2 , … , n y_{i}\left(\omega^{T} x_{i}+b\right) \geq 1, i=1,2, \ldots, n yi​(ωTxi​+b)≥1,i=1,2,…,n

条件二显然满足，因为本问题不存在等式约束

推导这个优化问题符合KKT条件

以上优化问题改写为下面的形式

min ⁡ f ( w ) = min ⁡ 1 2 ∥ w ∥ 2  s.t.  g i ( w ) = 1 − y i ( w T x i + b ) ≤ 0 \begin{array}{ll} & \min f(w)=\min \frac{1}{2}\|w\|^{2} \\ \text { s.t. } & g_{i}(w)=1-y_{i}\left(w^{T} x_{i}+b\right) \leq 0\end{array}  s.t. ​minf(w)=min21​∥w∥2gi​(w)=1−yi​(wTxi​+b)≤0​
引入松弛变量 a i 2 a_{i}^{2} ai2​ 得到 h i ( w , a i ) = g i ( w ) + a i 2 = 0 h_{i}\left(w, a_{i}\right)=g_{i}(w)+a_{i}^{2}=0 hi​(w,ai​)=gi​(w)+ai2​=0 。这里加平方主要为了不再引入新的约束条件，如果只引入 a i a_{i} ai​ 那必须要保证 a i ≥ 0 a_{i} \geq 0 ai​≥0 才能保证 h i ( w , a i ) = 0 h_{i}\left(w, a_{i}\right)=0 hi​(w,ai​)=0 ，这不符合我们的意愿。

由此将不等式约束转化为了等式约束，并得到 Lagrange 函数:

L ( w , α , a ) = f ( w ) + ∑ i = 1 n α i h i ( w ) = f ( w ) + ∑ i = 1 n α i [ g i ( w ) + a i 2 ] λ i ≥ 0 \begin{aligned} L(w, \alpha, a)&=f(w)+\sum_{i=1}^{n} \alpha_{i} h_{i}(w) \\ &=f(w)+\sum_{i=1}^{n} \alpha_{i}\left[g_{i}(w)+a_{i}^{2}\right] \quad \lambda_{i} \geq 0 \end{aligned} L(w,α,a)​=f(w)+i=1∑n​αi​hi​(w)=f(w)+i=1∑n​αi​[gi​(w)+ai2​]λi​≥0​

只是L式，为了推导简便，省略了参数b，大家不要疑惑这

由等式约束优化问题极值的必要条件对其求解，联立方程 :

{ ∂ L ∂ w i = ∂ f ∂ w i + ∑ i = 1 n α i ∂ g i ∂ w i = 0 ∂ L ∂ a i = 2 α i a i = 0 ∂ L ∂ α i = g i ( w ) + a i 2 = 0 α i ; ≥ 0 \left\{\begin{aligned} \frac{\partial L}{\partial w_{i}} &=\frac{\partial f}{\partial w_{i}}+\sum_{i=1}^{n} \alpha_{i} \frac{\partial g_{i}}{\partial w_{i}}=0 \\ \frac{\partial L}{\partial a_{i}} &=2 \alpha_{i} a_{i}=0 \\ \frac{\partial L}{\partial \alpha_{i}} &=g_{i}(w)+a_{i}^{2}=0 \\ \alpha_{i} &; \geq 0 \end{aligned}\right. ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧​∂wi​∂L​∂ai​∂L​∂αi​∂L​αi​​=∂wi​∂f​+i=1∑n​αi​∂wi​∂gi​​=0=2αi​ai​=0=gi​(w)+ai2​=0;≥0​

针对 α i a i = 0 \alpha_{i} a_{i}=0 αi​ai​=0 有两种情况:
情形一: α i = 0 , a i ≠ 0 \alpha_{i}=0, a_{i} \neq 0 αi​=0,ai​​=0
由于 α i = 0 \alpha_{i}=0 αi​=0 ，因此约束条件 g i ( w ) g_{i}(w) gi​(w) 不起作用，且 g i ( w ) < 0 g_{i}(w)<0 gi​(w)<0
情形二: α i ≠ 0 , a i = 0 \quad \alpha_{i} \neq 0, a_{i}=0 αi​​=0,ai​=0
此时 g i ( w ) = 0 g_{i}(w)=0 gi​(w)=0 且 α i > 0 \alpha_{i}>0 αi​>0 ，可以理解为约束条件 g i ( w ) g_{i}(w) gi​(w) 起作用了，且 g i ( w ) = 0 g_{i}(w)=0 gi​(w)=0
综合可得: α i g i ( w ) = 0 \alpha_{i} g_{i}(w)=0 αi​gi​(w)=0 ，且在约束条件起作用时 α i > 0 , g i ( w ) = 0 \alpha_{i}>0, g_{i}(w)=0 αi​>0,gi​(w)=0 ； 约束不起作用时 α i = 0 , g i ( w ) < 0 \alpha_{i}=0, g_{i}(w)<0 αi​=0,gi​(w)<0

由此方程组转换为:

{ ∂ L ∂ w i = ∂ f ∂ w i + ∑ j = 1 n α j ∂ g j ∂ w i = 0 （ 稳 定 性 条 件 ） α i g i ( w ) = 0 , （ 互 补 松 弛 条 件 ） g i ( w ) ≤ 0 （ 原 始 可 行 性 条 件 ） α i ≥ 0 （ 对 偶 可 行 性 条 件 ） \left\{\begin{aligned} \frac{\partial L}{\partial w_{i}} &=\frac{\partial f}{\partial w_{i}}+\sum_{j=1}^{n} \alpha_{j} \frac{\partial g_{j}}{\partial w_{i}}=0 （稳定性条件）\\ \alpha_{i} g_{i}(w) &=0, （互补松弛条件）\\ g_{i}(w) & \leq 0（原始可行性条件） \\ \alpha_{i} & \geq 0（对偶可行性条件） \end{aligned}\right. ⎩⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧​∂wi​∂L​αi​gi​(w)gi​(w)αi​​=∂wi​∂f​+j=1∑n​αj​∂wi​∂gj​​=0（稳定性条件）=0,（互补松弛条件）≤0（原始可行性条件）≥0（对偶可行性条件）​

以上便是不等式约束优化优化问题的 KKT(Karush-Kuhn-Tucker) 条件， α i \alpha_{i} αi​ 称为 KKT 乘子。

这个式子告诉了我们什么事情呢?
直观来讲就是，支持向量 g i ( w ) = 0 g_{i}(w)=0 gi​(w)=0 ，所以 α i > 0 \alpha_{i}>0 αi​>0 即可。而其他向量 g i ( w ) < 0 , α i = 0 g_{i}(w)<0, \alpha_{i}=0 gi​(w)<0,αi​=0.

1）KKT条件是对最优解的约束，而原始问题中的约束条件是对可行解的约束。

2）KKT条件的推导对于后面马上要介绍的拉格朗日对偶问题的推导很重要。

其实这段解释还有更形象化的图文解释，请参考https://zhuanlan.zhihu.com/p/24638007

关于拉格朗日乘子 α \alpha α为什么非负，https://zhuanlan.zhihu.com/p/24638007这篇文章也有解释。

但其实，我们毕竟是搞机器学习的，对于数学理论的证明，不必太过于深究，不要舍本逐末，本文推导已经很流畅了（个人觉得）

现在，凸优化问题和KKT都满足了，问题转换成了强对偶问题。而求解这个对偶学习问题，可以分为三个步骤：

  • 首先要让 L ( w , b , α ) L(w, b, \alpha) L(w,b,α) 关于 w w w 和 b b b 最小化
  • 然后求对 α \alpha α 的极大
  • 最后利用SMO算法求解对偶问题中的拉格朗日乘子

接下来，继续推导。

对偶问题求解

  1. 根据上述推导已知:
    max ⁡ α i ≥ 0 min ⁡ w , b L ( w , b , α ) = d ∗ L ( w , b , α ) = 1 2 ∥ w ∥ 2 − ∑ i = 1 n α i ( y i ( w T x i + b ) − 1 ) \begin{aligned} &\max _{\alpha_{i} \geq 0} \min _{w, b} \mathcal{L}(w, b, \alpha)=d^{*} \\ &\mathcal{L}(\boldsymbol{w}, b, \boldsymbol{\alpha})=\frac{1}{2}\|\boldsymbol{w}\|^{2}-\sum_{i=1}^{n} \alpha_{i}\left(y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right)-1\right) \end{aligned} ​αi​≥0max​w,bmin​L(w,b,α)=d∗L(w,b,α)=21​∥w∥2−i=1∑n​αi​(yi​(wTxi​+b)−1)​

    首先固定 α \alpha α ，要让 L ( w , b , α ) L(w, b, \alpha) L(w,b,α) 关于 w w w 和 b b b 最小化，分别对w和b偏导数，令其等于 0 , 即:
    ∂ L ∂ w = 0 ⇒ w = ∑ i = 1 n α i y i x i ∂ L ∂ b = 0 ⇒ ∑ i = 1 n α i y i = 0 \begin{aligned} \frac{\partial \mathcal{L}}{\partial \boldsymbol{w}} &=0 \Rightarrow \boldsymbol{w}=\sum_{i=1}^{n} \alpha_{i} y_{i} \boldsymbol{x}_{i} \\ \frac{\partial \mathcal{L}}{\partial b} &=0 \Rightarrow \sum_{i=1}^{n} \alpha_{i} y_{i}=0 \end{aligned} ∂w∂L​∂b∂L​​=0⇒w=i=1∑n​αi​yi​xi​=0⇒i=1∑n​αi​yi​=0​

    将上述结果带回 L ( w , b , α ) L(w, b, \alpha) L(w,b,α) 得到:
    L ( w , b , α ) = 1 2 ∥ w ∥ 2 − ∑ i = 1 n α i [ y i ( w T x i + b ) − 1 ] = 1 2 w T w − w T ∑ i = 1 n α i y i x i − b ∑ i = 1 n α i y i + ∑ i = 1 n α i = 1 2 w T ∑ i = 1 n α i y i x i − w T ∑ i = 1 n α i y i x i − b ⋅ 0 + ∑ i = 1 n α i = ∑ i = 1 n α i − 1 2 ( ∑ i = 1 n α i y i x i ) T ∑ i = 1 n α i y i x i = ∑ i = 1 n α i − 1 2 ∑ i , j = 1 n α i α j y i y j x i T x j \begin{aligned} \mathcal{L}(\boldsymbol{w}, b, \boldsymbol{\alpha}) &=\frac{1}{2}\|\boldsymbol{w}\|^{2}-\sum_{i=1}^{n} \alpha_{i}\left[y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right)-1\right] \\ &=\frac{1}{2} \boldsymbol{w}^{\mathrm{T}} \boldsymbol{w}-\boldsymbol{w}^{\mathrm{T}} \sum_{i=1}^{n} \alpha_{i} y_{i} \boldsymbol{x}_{i}-b \sum_{i=1}^{n} \alpha_{i} y_{i}+\sum_{i=1}^{n} \alpha_{i} \\ &=\frac{1}{2} \boldsymbol{w}^{\mathrm{T}} \sum_{i=1}^{n} \alpha_{i} y_{i} \boldsymbol{x}_{i}-\boldsymbol{w}^{\mathrm{T}} \sum_{i=1}^{n} \alpha_{i} y_{i} \boldsymbol{x}_{i}-b \cdot 0+\sum_{i=1}^{n} \alpha_{i} \\ &=\sum_{i=1}^{n} \alpha_{i}-\frac{1}{2}\left(\sum_{i=1}^{n} \alpha_{i} y_{i} \boldsymbol{x}_{i}\right)^{\mathrm{T}} \sum_{i=1}^{n} \alpha_{i} y_{i} \boldsymbol{x}_{i} \\ &=\sum_{i=1}^{n} \alpha_{i}-\frac{1}{2} \sum_{i, j=1}^{n} \alpha_{i} \alpha_{j} y_{i} y_{j} \boldsymbol{x}_{i}^{\mathrm{T}} \boldsymbol{x}_{j} \end{aligned} L(w,b,α)​=21​∥w∥2−i=1∑n​αi​[yi​(wTxi​+b)−1]=21​wTw−wTi=1∑n​αi​yi​xi​−bi=1∑n​αi​yi​+i=1∑n​αi​=21​wTi=1∑n​αi​yi​xi​−wTi=1∑n​αi​yi​xi​−b⋅0+i=1∑n​αi​=i=1∑n​αi​−21​(i=1∑n​αi​yi​xi​)Ti=1∑n​αi​yi​xi​=i=1∑n​αi​−21​i,j=1∑n​αi​αj​yi​yj​xiT​xj​​

    从上面的最后一个式子，可以看出，此时的 L ( w , b , α ) L(w, b, \alpha) L(w,b,α) 函数只含有一个变量，即 α i \alpha_i αi​。

  2. 现在内侧的最小值求解完成，求解外侧的最大值，从上面的式子得到
    max ⁡ α ∑ i = 1 n α i − 1 2 ∑ i , j = 1 n α i α j y i y j x i T x j  s.t.  α i ≥ 0 , i = 1 , 2 , ⋯   , n ∑ i = 1 n α i y i = 0 \begin{aligned} &\max _{\boldsymbol{\alpha}} \sum_{i=1}^{n} \alpha_{i}-\frac{1}{2} \sum_{i, j=1}^{n} \alpha_{i} \alpha_{j} y_{i} y_{j} \boldsymbol{x}_{i}^{\mathrm{T}} \boldsymbol{x}_{j} \\ &\text { s.t. } \alpha_{i} \geq 0, i=1,2, \cdots, n \\ &\sum_{i=1}^{n} \alpha_{i} y_{i}=0 \end{aligned} ​αmax​i=1∑n​αi​−21​i,j=1∑n​αi​αj​yi​yj​xiT​xj​ s.t. αi​≥0,i=1,2,⋯,ni=1∑n​αi​yi​=0​

现在优化问题变成了如上的形式。对于这个问题，有更高效的优化算法，即序列最小优 化 (SMO) 算法。通过这个优化算法能得到 α \alpha α ，再根据 α \alpha α ，就可以求解出 w w w和 b b b，进而求得最初的目的: 找到超平面，即"决策平面"。

SMO算法

Platt的SMO算法

1996年, John Platt发布了一个称为 SMO 的强大算法, 用于训练SVM。SMO表示序列最小优化 ( Sequential Minimal Optimization )。Platt的SMO算法是将大优化问题分解为多个小优化问题来 求解的。这些小优化问题往往很容易求解, 并且对它们进行顺序求解的结果与将它们作为整体来 求解的结果是完全一致的。在结果完全相同的同时, SMO算法的求解时间短很多。

SMO算法的目标是求出一系列 α \alpha α和 b b b,一旦求出了这些 α \alpha α, 就很容易计算出权重向量 w w w 并得到分隔超平面。

SMO算法的工作原理是：每次循环中选择两个 α \alpha α进行优化处理。一旦找到一对合适的 α \alpha α, 那么就增大其中一个同时减小另一个。这里所谓的 “合适” 就是指两个 α \alpha α必须要符合一定的条件, 条件之一就是这两个 α \alpha α必须要在间隔边界之外, 而其第二个条件则是这两个 α \alpha α 还没有进行过区间化处理或者不在边界上。

SMO算法的解法

先来定义特征到结果的输出函数为:

u = ω T x + b u=\omega^{T} x+b u=ωTx+b

接着，回忆一下原始优化问题，如下:

min ⁡ 1 2 ∥ ω ∥ 2  s.t.  y i ( ω T x i + b ) ≥ 1 , i = 1 , 2 , … , n \begin{aligned} &\min \frac{1}{2}\|\omega\|^{2} \\ &\text { s.t. } y_{i}\left(\omega^{T} x_{i}+b\right) \geq 1, i=1,2, \ldots, n \end{aligned} ​min21​∥ω∥2 s.t. yi​(ωTxi​+b)≥1,i=1,2,…,n​

求导得:

ω = ∑ i = 1 n α i y i x i \boldsymbol{\omega}=\sum_{i=1}^{n} \alpha_{i} y_{i} \boldsymbol{x}_{\boldsymbol{i}} ω=i=1∑n​αi​yi​xi​

将上述公式带入输出函数中:

u = ∑ i = 1 n α i y i x i T x + b u=\sum_{i=1}^{n} \alpha_{i} y_{i} x_{i}^{T} x+b u=i=1∑n​αi​yi​xiT​x+b

与此同时，拉格朗日对偶后得到最终的目标化函数:

max ⁡ α ∑ i = 1 n α i − 1 2 ∑ i , j = 1 n α i α j y i y j x i T x j  s.t.  α i ≥ 0 , i = 1 , 2 , ⋯   , n ∑ i = 1 n α i y i = 0 \begin{aligned} \max _{\alpha} & \sum_{i=1}^{n} \alpha_{i}-\frac{1}{2} \sum_{i, j=1}^{n} \alpha_{i} \alpha_{j} y_{i} y_{j} x_{i}^{\mathrm{T}} x_{j} \\ \text { s.t. } \alpha_{i} & \geq 0, i=1,2, \cdots, n \\ & \sum_{i=1}^{n} \alpha_{i} y_{i}=0 \end{aligned} αmax​ s.t. αi​​i=1∑n​αi​−21​i,j=1∑n​αi​αj​yi​yj​xiT​xj​≥0,i=1,2,⋯,ni=1∑n​αi​yi​=0​

将目标函数变形，在前面增加一个负号，将最大值问题转换成最小值问题：

min ⁡ α 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j x i T x j − ∑ i = 1 n α i \min _{\alpha} \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_{i} \alpha_{j} y_{i} y_{j} \boldsymbol{x}_{i}{ }^{T} \boldsymbol{x}_{j}-\sum_{i=1}^{n} \alpha_{i} αmin​21​i=1∑n​j=1∑n​αi​αj​yi​yj​xi​Txj​−i=1∑n​αi​

 s.t.  α i ≥ 0 , i = 1 , 2 , ⋯   , n ∑ i = 1 n α i y i = 0 \begin{aligned} &\text { s.t. } \alpha_{i} \geq 0, \quad i=1,2, \cdots, n \\ &\quad \sum_{i=1}^{n} \alpha_{i} y_{i}=0 \end{aligned} ​ s.t. αi​≥0,i=1,2,⋯,ni=1∑n​αi​yi​=0​

实际上，对于上述目标函数，是存在一个假设的，即数据100%线性可分。但是，目前为止，我们知道几乎所有数据都不那么"干净"。这时我们就可以通过引入所谓的 松弛变量 (slack variable)，来允许有些数据点可以处于超平面的错误的一侧。这样我们的优化目标就能保持仍然不变，但是此时我们的约束条件有所改变：

推导过程：

原始最优化问题的拉格朗日函数是

L ( w , b , ξ , α , μ ) ≡ 1 2 ∥ w ∥ 2 + C ∑ i = 1 N ξ i − ∑ i = 1 N α i ( y i ( w ⋅ x i + b ) − 1 + ξ i ) − ∑ i = 1 N μ i ξ i L(w, b, \xi, \alpha, \mu) \equiv \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{N} \xi_{i}-\sum_{i=1}^{N} \alpha_{i}\left(y_{i}\left(w \cdot x_{i}+b\right)-1+\xi_{i}\right)-\sum_{i=1}^{N} \mu_{i} \xi_{i} L(w,b,ξ,α,μ)≡21​∥w∥2+Ci=1∑N​ξi​−i=1∑N​αi​(yi​(w⋅xi​+b)−1+ξi​)−i=1∑N​μi​ξi​

其中, α i ⩾ 0 , μ i ⩾ 0 \alpha_{i} \geqslant 0, \mu_{i} \geqslant 0 αi​⩾0,μi​⩾0 。
对偶问题是拉格朗日函数的极大极小问题。首先求 L ( w , b , ξ , α , μ ) L(w, b, \xi, \alpha, \mu) L(w,b,ξ,α,μ) 对 w , b , ξ w, b, \xi w,b,ξ 的极小, 由

∇ w L ( w , b , ξ , α , μ ) = w − ∑ i = 1 N α i y i x i = 0 ∇ b L ( w , b , ξ , α , μ ) = − ∑ i = 1 N α i y i = 0 ∇ ξ 1 L ( w , b , ξ , α , μ ) = C − α i − μ i = 0 \begin{aligned} &\nabla_{w} L(w, b, \xi, \alpha, \mu)=w-\sum_{i=1}^{N} \alpha_{i} y_{i} x_{i}=0 \\ &\nabla_{b} L(w, b, \xi, \alpha, \mu)=-\sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\ &\nabla_{\xi_{1}} L(w, b, \xi, \alpha, \mu)=C-\alpha_{i}-\mu_{i}=0 \end{aligned} ​∇w​L(w,b,ξ,α,μ)=w−i=1∑N​αi​yi​xi​=0∇b​L(w,b,ξ,α,μ)=−i=1∑N​αi​yi​=0∇ξ1​​L(w,b,ξ,α,μ)=C−αi​−μi​=0​

得

w = ∑ i = 1 N α i y i x i w=\sum_{i=1}^{N} \alpha_{i} y_{i} x_{i} w=i=1∑N​αi​yi​xi​

∑ i = 1 N α i y i = 0 C − α i − μ i = 0 \begin{gathered} \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\ C-\alpha_{i}-\mu_{i}=0 \end{gathered} i=1∑N​αi​yi​=0C−αi​−μi​=0​

将上面三个式子代入式 L ( w , b , ξ , α , μ ) ≡ 1 2 ∥ w ∥ 2 + C ∑ i = 1 N ξ i − ∑ i = 1 N α i ( y i ( w ⋅ x i + b ) − 1 + ξ i ) − ∑ i = 1 N μ i ξ i L(w, b, \xi, \alpha, \mu) \equiv \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{N} \xi_{i}-\sum_{i=1}^{N} \alpha_{i}\left(y_{i}\left(w \cdot x_{i}+b\right)-1+\xi_{i}\right)-\sum_{i=1}^{N} \mu_{i} \xi_{i} L(w,b,ξ,α,μ)≡21​∥w∥2+C∑i=1N​ξi​−∑i=1N​αi​(yi​(w⋅xi​+b)−1+ξi​)−∑i=1N​μi​ξi​, 得

min ⁡ w , b , ξ L ( w , b , ξ , α , μ ) = − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) + ∑ i = 1 N α i \min _{w, b, \xi} L(w, b, \xi, \alpha, \mu)=-\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)+\sum_{i=1}^{N} \alpha_{i} w,b,ξmin​L(w,b,ξ,α,μ)=−21​i=1∑N​j=1∑N​αi​αj​yi​yj​(xi​⋅xj​)+i=1∑N​αi​

再对 min ⁡ w , b , ξ L ( w , b , ξ , α , μ ) \min _{w, b, \xi} L(w, b, \xi, \alpha, \mu) minw,b,ξ​L(w,b,ξ,α,μ) 求 α \alpha α 的极大, 即得对偶问题:

max ⁡ α − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) + ∑ i = 1 N α i  s.t.  ∑ i = 1 N α i y i = 0 C − α i − μ i = 0 α i ⩾ 0 μ i ⩾ 0 , i = 1 , 2 , ⋯   , N \begin{array}{ll} \max _{\alpha} & -\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)+\sum_{i=1}^{N} \alpha_{i} \\ \text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\ & C-\alpha_{i}-\mu_{i}=0 \\ & \alpha_{i} \geqslant 0 \\ & \mu_{i} \geqslant 0, \quad i=1,2, \cdots, N \end{array} maxα​ s.t. ​−21​∑i=1N​∑j=1N​αi​αj​yi​yj​(xi​⋅xj​)+∑i=1N​αi​∑i=1N​αi​yi​=0C−αi​−μi​=0αi​⩾0μi​⩾0,i=1,2,⋯,N​

C − α i − μ i = 0 = > C − α i = μ i , ∵ μ i ⩾ 0 ， ∴ C − α i = μ i ⩾ 0 , = > α i ⩽ C , 又 ∵ α i ⩾ 0 ， ∴ C-\alpha_{i}-\mu_{i}=0=>C-\alpha_{i}=\mu_{i},∵\mu_{i} \geqslant 0 ，∴C-\alpha_{i}=\mu_{i} \geqslant 0 ,=>\alpha_{i} \leqslant C,又∵\alpha_{i} \geqslant 0，∴ C−αi​−μi​=0=>C−αi​=μi​,∵μi​⩾0，∴C−αi​=μi​⩾0,=>αi​⩽C,又∵αi​⩾0，∴ 0 ⩽ α i ⩽ C 0 \leqslant \alpha_{i} \leqslant C 0⩽αi​⩽C

再将对目标函数求极大转换为求极小, 于是得到对偶问题 min ⁡ α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i  s.t.  ∑ i = 1 N α i y i = 0 0 ⩽ α i ⩽ C , i = 1 , 2 , ⋯   , N \begin{array}{ll}\min _{\alpha} & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} \\\text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\& 0 \leqslant \alpha_{i} \leqslant C, \quad i=1,2, \cdots, N\end{array} minα​ s.t. ​21​∑i=1N​∑j=1N​αi​αj​yi​yj​(xi​⋅xj​)−∑i=1N​αi​∑i=1N​αi​yi​=00⩽αi​⩽C,i=1,2,⋯,N​ 。 可以通过求解对偶问题而得到原始问题的解, 进而确定分离超平面和决策函数。 为此, 就可以定理的形式叙述原始问题的最优解和对偶问题的最优解的关系。

min ⁡ w , b , ξ 1 2 ∥ w ⃗ ∥ 2 + C ∑ i = 1 N ξ i \min _{w, b, \xi} \frac{1}{2}\|\vec{w}\|^{2}+C \sum_{i=1}^{N} \xi_{i} w,b,ξmin​21​∥w ∥2+Ci=1∑N​ξi​

 subject to  y i ( w ⃗ ⋅ x ⃗ i − b ) ≥ 1 − ξ i , ∀ i \text { subject to } y_{i}\left(\vec{w} \cdot \vec{x}_{i}-b\right) \geq 1-\xi_{i}, \forall i  subject to yi​(w ⋅x i​−b)≥1−ξi​,∀i

0 ≤ α i ≤ C , ∀ i 0 \leq \alpha_{i} \leq C, \forall i 0≤αi​≤C,∀i

化简得

min ⁡ α a m p ; 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i  s.t.  a m p ; ∑ i = 1 N α i y i = 0 a m p ; 0 ⩽ α i ⩽ C , i = 1 , 2 , ⋯   , N \begin{array}{ll}\min _{\alpha} &amp; \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} \\\text { s.t. } &amp; \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\&amp; 0 \leqslant \alpha_{i} \leqslant C, \quad i=1,2, \cdots, N\end{array} minα​ s.t. ​amp;21​∑i=1N​∑j=1N​αi​αj​yi​yj​(xi​⋅xj​)−∑i=1N​αi​amp;∑i=1N​αi​yi​=0amp;0⩽αi​⩽C,i=1,2,⋯,N​

根据KKT条件可以得出其中 α i \alpha_i αi​取值的意义为:

以下是KKT条件

∇ w L ( w ∗ , b ∗ , ξ ∗ , α ∗ , μ ∗ ) = w ∗ − ∑ i = 1 N α i ∗ y i x i = 0 \nabla_{w} L\left(w^{*}, b^{*}, \xi^{*}, \alpha^{*}, \mu^{*}\right)=w^{*}-\sum_{i=1}^{N} \alpha_{i}^{*} y_{i} x_{i}=0 ∇w​L(w∗,b∗,ξ∗,α∗,μ∗)=w∗−i=1∑N​αi∗​yi​xi​=0

∇ b L ( w ∗ , b ∗ , ξ ∗ , α ∗ , μ ∗ ) = − ∑ i = 1 N α i ∗ y i = 0 ∇ ξ L ( w ∗ , b ∗ , ξ ∗ , α ∗ , μ ∗ ) = C − α ∗ − μ ∗ = 0 α i ∗ ( y i ( w ∗ ⋅ x i + b ∗ ) − 1 + ξ i ∗ ) = 0 μ i ∗ ξ i ∗ = 0 \begin{gathered} \nabla_{b} L\left(w^{*}, b^{*}, \xi^{*}, \alpha^{*}, \mu^{*}\right)=-\sum_{i=1}^{N} \alpha_{i}^{*} y_{i}=0 \\ \nabla_{\xi} L\left(w^{*}, b^{*}, \xi^{*}, \alpha^{*}, \mu^{*}\right)=C-\alpha^{*}-\mu^{*}=0 \\ \alpha_{i}^{*}\left(y_{i}\left(w^{*} \cdot x_{i}+b^{*}\right)-1+\xi_{i}^{*}\right)=0 \\ \mu_{i}^{*} \xi_{i}^{*}=0 \end{gathered} ∇b​L(w∗,b∗,ξ∗,α∗,μ∗)=−i=1∑N​αi∗​yi​=0∇ξ​L(w∗,b∗,ξ∗,α∗,μ∗)=C−α∗−μ∗=0αi∗​(yi​(w∗⋅xi​+b∗)−1+ξi∗​)=0μi∗​ξi∗​=0​
y i ( w ∗ ⋅ x i + b ∗ ) − 1 + ξ i ∗ ⩾ 0 ξ i ∗ ⩾ 0 α i ∗ ⩾ 0 μ i ∗ ⩾ 0 , i = 1 , 2 , ⋯   , N \begin{gathered} y_{i}\left(w^{*} \cdot x_{i}+b^{*}\right)-1+\xi_{i}^{*} \geqslant 0 \\ \xi_{i}^{*} \geqslant 0 \\ \alpha_{i}^{*} \geqslant 0 \\ \mu_{i}^{*} \geqslant 0, \quad i=1,2, \cdots, N \end{gathered} yi​(w∗⋅xi​+b∗)−1+ξi∗​⩾0ξi∗​⩾0αi∗​⩾0μi∗​⩾0,i=1,2,⋯,N​

α i = 0 ⇔ y i u i ≥ 1 0 < α i < C ⇔ y i u i = 1 α i = C ⇔ y i u i ≤ 1 \begin{aligned} \alpha_{i}=0 & \Leftrightarrow y_{i} u_{i} \geq 1 \\ 0<\alpha_{i}<C & \Leftrightarrow y_{i} u_{i}=1 \\ \alpha_{i}=C & \Leftrightarrow y_{i} u_{i} \leq 1 \end{aligned} αi​=00<αi​<Cαi​=C​⇔yi​ui​≥1⇔yi​ui​=1⇔yi​ui​≤1​

这个KKT条件说明，在两条间隔线外面的点，对应前面的系数 α i \alpha_{i} αi​ 为 0 ，在两条间隔线里面的对应 α i \alpha_{i} αi​ 为 C C C ，在两条间隔线上的对应的系数 α i \alpha_{i} αi​ 在0和 C C C之间。

而最优解需要满足KKT条件，即上述 3 个条件都得满足，以下几种情况出现将会不满足：

y i u i ≤ 1 α i < C y i u i ≥ 1 α i > 0 y i u i = 1 α i = 0  或者  α i = C \begin{gathered} \mathrm{y}_{i} u_{i} \leq 1 \quad \alpha_{i}<C \\ \mathrm{y}_{i} u_{i} \geq 1 \quad \alpha_{i}>0 \\ \mathrm{y}_{i} u_{i}=1 \quad \alpha_{i}=0 \text { 或者 } \alpha_{i}=\mathrm{C} \end{gathered} yi​ui​≤1αi​<Cyi​ui​≥1αi​>0yi​ui​=1αi​=0 或者 αi​=C​

也就是说，如果存在不能满足KKT条件的 α \alpha α ，那么需要更新这些 α i \alpha_i αi​ ，这是第一个约束条件。此外， 更新的同时还要受到第二个约束条件的限制，即：

∑ i = 1 n α i y i = 0 \sum_{i=1}^{n} \alpha_{i} y_{i}=0 i=1∑n​αi​yi​=0

因为这个条件, 我们同时更新两个 α \alpha α 值, 因为只有成对更新, 才能保证更新之后的值仍然满足和为 0 的约束，假设我们选择的两个乘子为 α 1 \alpha 1 α1 和 α 2 \alpha 2 α2 :

α 1 n e w y 1 + α 2 n e w y 2 = α 1 o l d y 1 + α 2 o l d y 2 = ζ \alpha_{1}^{n e w} y_{1}+\alpha_{2}^{n e w} y_{2}=\alpha_{1}^{o l d} y_{1}+\alpha_{2}^{o l d} y_{2}=\zeta α1new​y1​+α2new​y2​=α1old​y1​+α2old​y2​=ζ

其中， ζ \zeta ζ为常数。因为两个因子不好同时求解，所以可以先求第二个乘子 α 2 \alpha_2 α2​ 的解 ( α 2 n e w \alpha_2^{new} α2new​ )， 得到 α 2 \alpha_2 α2​ 的解 ( α 2 n e w \alpha_2^{new} α2new​ ) 之后, 再用 α 2 \alpha_2 α2​ 的解 ( α 2 n e w \alpha_2^{new} α2new​ ) 表示 α 1 \alpha_1 α1​ 的解 ( α 1 n e w \alpha_1^{new} α1new​ )。为了求解 α 2 n e w \alpha_2^{new} α2new​ ，得先确定 α 2 n e w \alpha_2^{new} α2new​ 的取值范围。假设它的上下边界分别为H和L，那会有:

L ≤ α 2 n e w ≤ H L \leq \alpha_{2}^{n e w} \leq H L≤α2new​≤H

接下来，综合下面两个条件:

C ≥ α i ≥ 0 , i = 1 , 2 , ⋯   , n α 1 n e w y 1 + α 2 n e w y 2 = α 1 old  y 1 + α 2 old  y 2 = ζ \begin{aligned} &C \geq \alpha_{i} \geq 0, \quad i=1,2, \cdots, n \\ &\alpha_{1}^{n e w} y_{1}+\alpha_{2}^{n e w} y_{2}=\alpha_{1}^{\text {old }} y_{1}+\alpha_{2}^{\text {old }} y_{2}=\zeta \end{aligned} ​C≥αi​≥0,i=1,2,⋯,nα1new​y1​+α2new​y2​=α1old ​y1​+α2old ​y2​=ζ​

当 y 1 y_1 y1​ 不等于 y 2 y_2 y2​ 时，即一个为正 1 ， 一 1 ， 一 1，一 个为负 1 的时侯，可以得到:

α 1 o l d − α 2 o l d = ζ \alpha_{1}^{o l d}-\alpha_{2}^{o l d}=\zeta α1old​−α2old​=ζ

所以有:

L = max ⁡ ( 0 , − ζ ) , H = min ⁡ ( C , C − ζ ) L=\max (0,-\zeta), \quad H=\min (C, C-\zeta) L=max(0,−ζ),H=min(C,C−ζ)

α 1 old  + α 2 old  = ζ \alpha_{1}^{\text {old }}+\alpha_{2}^{\text {old }}=\zeta α1old ​+α2old ​=ζ

所以有:

L = max ⁡ ( 0 , ζ − C ) , H = min ⁡ ( C , ζ ) L=\max (0, \zeta-C), \quad H=\min (C, \zeta) L=max(0,ζ−C),H=min(C,ζ)

如此，根据 y 1 y_1 y1​和 y 2 y_2 y2​ 异号或同号，可以得出 α 2 n e w \alpha_2^{new} α2new​ 的上下界分别为:

{ L = max ⁡ ( 0 , α 2 o l d − α 1 o l d ) , H = min ⁡ ( C , C + α 2 o l d − α 1 o l d )  if  y 1 ≠ y 2 L = max ⁡ ( 0 , α 2 o l d + α 1 o l d − C ) , H = min ⁡ ( C , α 2 o l d + α 1 o l d )  if  y 1 = y 2 \left\{\begin{array}{l} L=\max \left(0, \alpha_{2}^{o l d}-\alpha_{1}^{o l d}\right), H=\min \left(C, C+\alpha_{2}^{o l d}-\alpha_{1}^{o l d}\right) \quad \text { if } y_{1} \neq y_{2} \\ L=\max \left(0, \alpha_{2}^{o l d}+\alpha_{1}^{o l d}-C\right), H=\min \left(C, \alpha_{2}^{o l d}+\alpha_{1}^{o l d}\right) \quad \text { if } y_{1}=y_{2} \end{array}\right. {L=max(0,α2old​−α1old​),H=min(C,C+α2old​−α1old​) if y1​​=y2​L=max(0,α2old​+α1old​−C),H=min(C,α2old​+α1old​) if y1​=y2​​

这个界限就是编程的时候需要用到的。已经确定了边界，接下来，就是推导迭代式，用于更新 α \alpha α 值。

  • 以下是补充推导， K K K是核函数
  • 选择两个变量，其它变量固定
  • SMO将对偶问题转化成一系列子问题：

min ⁡ α 1 , α 2 W ( α 1 , α 2 ) 2 = 1 2 K 11 α 1 2 + 1 2 K 22 α 2 2 + y 1 y 2 K 12 α 1 α 2 − ( α 1 + α 2 ) + y 1 α 1 ∑ i = 3 N y i α i K i 1 + y 2 α 2 ∑ i = 3 N y i α i K i 2  s.t.  α 1 y 1 + α 2 y 2 = − ∑ i = 3 N y i α i = ζ 0 ≤ α i ≤ C , i = 1 , 2 \begin{aligned} \min _{\alpha_{1}, \alpha_{2}} & \frac{W\left(\alpha_{1}, \alpha_{2}\right)}{2}=\frac{1}{2} K_{11} \alpha_{1}^{2}+\frac{1}{2} K_{22} \alpha_{2}^{2}+y_{1} y_{2} K_{12} \alpha_{1} \alpha_{2} \\ &-\left(\alpha_{1}+\alpha_{2}\right)+y_{1} \alpha_{1} \sum_{i=3}^{N} y_{i} \alpha_{i} K_{i 1}+y_{2} \alpha_{2} \sum_{i=3}^{N} y_{i} \alpha_{i} K_{i 2} \\ \text { s.t. } & \alpha_{1} y_{1}+\alpha_{2} y_{2}=-\sum_{i=3}^{N} y_{i} \alpha_{i}=\zeta \\ & 0 \leq \alpha_{i} \leq C, i=1,2 \end{aligned} α1​,α2​min​ s.t. ​2W(α1​,α2​)​=21​K11​α12​+21​K22​α22​+y1​y2​K12​α1​α2​−(α1​+α2​)+y1​α1​i=3∑N​yi​αi​Ki1​+y2​α2​i=3∑N​yi​αi​Ki2​α1​y1​+α2​y2​=−i=3∑N​yi​αi​=ζ0≤αi​≤C,i=1,2​

  • 根据约束条件, α 2 \alpha_{2} α2​ 可以表示成 α 1 \alpha_{1} α1​ 的函数
  • 优化问题可以有解析解
  • 基于初始可行解 α 1 old  α 2 old  \alpha_{1}^{\text {old }} \alpha_{2}^{\text {old }} α1old ​α2old ​, 可以得到 α 1 new  α 2 new  \alpha_{1}^{\text {new }} \alpha_{2}^{\text {new }} α1new ​α2new ​

min ⁡ α 1 , α 2 W ( α 1 , α 2 ) = 1 2 K 11 α 1 2 + 1 2 K 22 α 2 2 + y 1 y 2 K 12 α 1 α 2 − ( α 1 + α 2 ) + y 1 α 1 ∑ i = 3 N y i α i K i 1 + y 2 α 2 ∑ i = 3 N y i α i K i 2  s.t.  α 1 y 1 + α 2 y 2 = − ∑ i = 3 N y i α i = ζ 0 ≤ α i ≤ C , i = 1 , 2 \begin{array}{rl} \min _{\alpha_{1}, \alpha_{2}} & W\left(\alpha_{1}, \alpha_{2}\right)=\frac{1}{2} K_{11} \alpha_{1}^{2}+\frac{1}{2} K_{22} \alpha_{2}^{2}+y_{1} y_{2} K_{12} \alpha_{1} \alpha_{2} \\ & -\left(\alpha_{1}+\alpha_{2}\right)+y_{1} \alpha_{1} \sum_{i=3}^{N} y_{i} \alpha_{i} K_{i 1}+y_{2} \alpha_{2} \sum_{i=3}^{N} y_{i} \alpha_{i} K_{i 2} \\ \text { s.t. } & \alpha_{1} y_{1}+\alpha_{2} y_{2}=-\sum_{i=3}^{N} y_{i} \alpha_{i}=\zeta \\ & 0 \leq \alpha_{i} \leq C, i=1,2 \end{array} minα1​,α2​​ s.t. ​W(α1​,α2​)=21​K11​α12​+21​K22​α22​+y1​y2​K12​α1​α2​−(α1​+α2​)+y1​α1​∑i=3N​yi​αi​Ki1​+y2​α2​∑i=3N​yi​αi​Ki2​α1​y1​+α2​y2​=−∑i=3N​yi​αi​=ζ0≤αi​≤C,i=1,2​

  • 两个变量,约束条件用二维空间中的图形表示
    在这里插入图片描述

  • 根据不等式条件 α 2 n e w \alpha_{2}^{n e w} α2new​ 的取值范围：
    L ≤ α 2 new  ≤ H L = max ⁡ ( 0 , α 2 old  − α 1 old  ) H = min ⁡ ( C , C + α 2 old  − α 1 old  ) \begin{gathered} L \leq \alpha_{2}^{\text {new }} \leq H \\ L=\max \left(0, \alpha_{2}^{\text {old }}-\alpha_{1}^{\text {old }}\right) \quad H=\min \left(C, C+\alpha_{2}^{\text {old }}-\alpha_{1}^{\text {old }}\right) \end{gathered} L≤α2new ​≤HL=max(0,α2old ​−α1old ​)H=min(C,C+α2old ​−α1old ​)​

    在这里插入图片描述
    ∵ α 1 ∈ [ 0 , C ] ∴ k − α 1 ∈ [ k , k − C ] α 2 ∈ [ k , k − C ] α 2 ∈ [ α 1 + α 2 , α 1 + α 2 − C ] α 2 ∈ [ 0 , C ] } ⇒ L = max ⁡ ( 0 , α 2 old  − α 1 old  ) H = min ⁡ ( C , C + α 2 old  − α 1 old  ) ∵\alpha_1 \in [0,C]\\∴k-\alpha_1 \in [k,k-C]\\\alpha_2 \in [k,k-C]\\\left.\begin{matrix} \alpha_2 \in [\alpha_1+\alpha_2,\alpha_1+\alpha_2-C] \\ \alpha_2 \in [0,C] \end{matrix}\right\}\Rightarrow L=\max \left(0, \alpha_{2}^{\text {old }}-\alpha_{1}^{\text {old }}\right) \quad H=\min \left(C, C+\alpha_{2}^{\text {old }}-\alpha_{1}^{\text {old }}\right) ∵α1​∈[0,C]∴k−α1​∈[k,k−C]α2​∈[k,k−C]α2​∈[α1​+α2​,α1​+α2​−C]α2​∈[0,C]​}⇒L=max(0,α2old ​−α1old ​)H=min(C,C+α2old ​−α1old ​)
    同理，如果 y 1 = y 2 y_1=y_2 y1​=y2​,则 L = max ⁡ ( 0 , α 2 old  + α 1 old  − C ) , H = min ⁡ ( C , α 2 old  + α 1 old  ) L=\max \left(0, \alpha_{2}^{\text {old }}+\alpha_{1}^{\text {old }}-C\right), \quad H=\min \left(C, \alpha_{2}^{\text {old }}+\alpha_{1}^{\text {old }}\right) L=max(0,α2old ​+α1old ​−C),H=min(C,α2old ​+α1old ​)

这段推导摘自我的博客https://blog.csdn.net/wl1780852311/article/details/119493842，其中符号和这篇博客不统一，有兴趣可以看一下那篇博客

这个界限就是编程的时候需要用到的。已经确定了边界，接下来，就是推导迭代式，用于更新 α \alpha α 值。

已经知道，更新 α \alpha α 的边界，接下来就是讨论如何更新 α \alpha α 值。依然假设选择的两个乘子为 α 1 \alpha_1 α1​ 和 α 2 \alpha_2 α2​ 。固定这两个乘子，进行推导。于是目标函数变成了:

W ( a 2 ) = ∑ i = 1 n α i − 1 2 ∑ i = 1 n ∑ j = 1 n y i y j x i T x j α i α j = α 1 + α 2 + ∑ i = 3 n α i − 1 2 ∑ i = 1 n ( ∑ j = 1 2 y i y j α i α j x i T x j + ∑ j = 3 n y i y j α i α j x i T x j ) = α 1 + α 2 + ∑ i = 3 n α i − 1 2 ∑ i = 1 2 ( ∑ j = 1 2 y i y j α i α j x i T x j + ∑ j = 3 n y i y j α i α j x i T x j ) − 1 2 ∑ i = 3 n ( ∑ j = 1 2 y i y j α i α j x i T x j + ∑ j = 3 n y i y j α i α j x i T x j ) = α 1 + α 2 + ∑ i = 3 n α i − 1 2 ∑ i = 1 2 ∑ j = 1 2 y i y j α i α j x i T x j − ∑ i = 1 2 ∑ j = 3 n y i y j α i α j x i T x j − 1 2 ∑ i = 3 n ∑ j = 3 n y i y j α i α j x i T x j = α 1 + α 2 − 1 2 α 1 2 x 1 T x 1 − 1 2 α 2 2 x 2 T x 2 − y 1 y 2 α 1 α 2 x 1 T x 2 − y 1 α 1 ∑ j = 3 n α j y j x 1 T x j − y 2 α 2 ∑ j = 3 n α j y j x 2 T x j + ∑ i = 3 n α i − 1 2 ∑ i = 3 n ∑ j = 3 n y i y j α i α j x i T x j \begin{aligned} &W\left(a_{2}\right)=\sum_{i=1}^{n} \alpha_{i}-\frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} y_{i} y_{j}{\boldsymbol{x}}_{i}{ }^{T} \boldsymbol{x}_{j} \alpha_{i} \alpha_{j}\\ &=\alpha_{1}+\alpha_{2}+\sum_{i=3}^{n} \alpha_{i}-\frac{1}{2} \sum_{i=1}^{n}\left(\sum_{j=1}^{2} y_{i} y_{j} \alpha_{i} \alpha_{j} \boldsymbol{x}_{i}{ }^{T} \boldsymbol{x}_{j}+\sum_{j=3}^{n} y_{i} y_{j} \alpha_{i} \alpha_{j} \boldsymbol{x}_{i}{ }^{T} \boldsymbol{x}_{j}\right)\\ &=\alpha_{1}+\alpha_{2}+\sum_{i=3}^{n} \alpha_{i}-\frac{1}{2} \sum_{i=1}^{2}\left(\sum_{j=1}^{2} y_{i} y_{j} \alpha_{i} \alpha_{j}{\boldsymbol{x}}_{i}{ }^{T} \boldsymbol{x}_{j}+\sum_{j=3}^{n} y_{i} y_{j} \alpha_{i} \alpha_{j} \boldsymbol{x}_{i}{ }^{T} \boldsymbol{x}_{j}\right)\\ &-\frac{1}{2} \sum_{i=3}^{n}\left(\sum_{j=1}^{2} y_{i} y_{j} \alpha_{i} \alpha_{j} \boldsymbol{x}_{i}^{T} \boldsymbol{x}_{j}+\sum_{j=3}^{n} y_{i} y_{j} \alpha_{i} \alpha_{j} \boldsymbol{x}_{i}^{T} \boldsymbol{x}_{j}\right)\\ &=\alpha_{1}+\alpha_{2}+\sum_{i=3}^{n} \alpha_{i}-\frac{1}{2} \sum_{i=1}^{2} \sum_{j=1}^{2} y_{i} y_{j} \alpha_{i} \alpha_{j} x_{i}^{T} x_{j}-\sum_{i=1}^{2} \sum_{j=3}^{n} y_{i} y_{j} \alpha_{i} \alpha_{j} x_{i}^{T} x_{j}\\ &-\frac{1}{2} \sum_{i=3}^{n} \sum_{j=3}^{n} y_{i} y_{j} \alpha_{i} \alpha_{j} x_{i}{ }^{T} x_{j}\\ &=\alpha_{1}+\alpha_{2}-\frac{1}{2} \alpha_{1}{ }^{2}{x_{1}}^{T} \boldsymbol{x}_{1}-\frac{1}{2} \alpha_{2}{ }^{2} \boldsymbol{x}_{2}{ }^{T} \boldsymbol{x}_{2}-y_{1} y_{2} \alpha_{1} \alpha_{2} \boldsymbol{x}_{1}{ }^{T} \boldsymbol{x}_{2}-y_{1} \alpha_{1} \sum_{j=3}^{n} \alpha_{j} y_{j} \boldsymbol{x}_{1}{ }^{T} \boldsymbol{x}_{j}\\ &-y_{2} \alpha_{2} \sum_{j=3}^{n} \alpha_{j} y_{j} \boldsymbol{x}_{2}{ }^{T} \boldsymbol{x}_{j}+\sum_{i=3}^{n} \alpha_{i}-\frac{1}{2} \sum_{i=3}^{n} \sum_{j=3}^{n} y_{i} y_{j} \alpha_{i} \alpha_{j} \boldsymbol{x}_{i}{ }^{T} \boldsymbol{x}_{j} \end{aligned} ​W(a2​)=i=1∑n​αi​−21​i=1∑n​j=1∑n​yi​yj​xi​Txj​αi​αj​=α1​+α2​+i=3∑n​αi​−21​i=1∑n​(j=1∑2​yi​yj​αi​αj​xi​Txj​+j=3∑n​yi​yj​αi​αj​xi​Txj​)=α1​+α2​+i=3∑n​αi​−21​i=1∑2​(j=1∑2​yi​yj​αi​αj​xi​Txj​+j=3∑n​yi​yj​αi​αj​xi​Txj​)−21​i=3∑n​(j=1∑2​yi​yj​αi​αj​xiT​xj​+j=3∑n​yi​yj​αi​αj​xiT​xj​)=α1​+α2​+i=3∑n​αi​−21​i=1∑2​j=1∑2​yi​yj​αi​αj​xiT​xj​−i=1∑2​j=3∑n​yi​yj​αi​αj​xiT​xj​−21​i=3∑n​j=3∑n​yi​yj​αi​αj​xi​Txj​=α1​+α2​−21​α1​2x1​Tx1​−21​α2​2x2​Tx2​−y1​y2​α1​α2​x1​Tx2​−y1​α1​j=3∑n​αj​yj​x1​Txj​−y2​α2​j=3∑n​αj​yj​x2​Txj​+i=3∑n​αi​−21​i=3∑n​j=3∑n​yi​yj​αi​αj​xi​Txj​​

为了描述方便，我们定义如下符号:

f ( x i ) = ∑ j = 1 n α j y j x i T x j + b f\left(\boldsymbol{x}_{i}\right)=\sum_{j=1}^{n} \alpha_{j} y_{j} \boldsymbol{x}_{i}{ }^{T} \boldsymbol{x}_{j}+b f(xi​)=j=1∑n​αj​yj​xi​Txj​+b

v i = ∑ j = 3 n α j y j x i T x j = f ( x i ) − ∑ j = 1 2 α j y j x i T x j − b \begin{aligned} {v_{i}=\sum_{j=3}^{n} \alpha_{j} y_{j} \boldsymbol{x}_{i}{ }^{T} \boldsymbol{x}_{j}=f\left(\boldsymbol{x}_{i}\right)-\sum_{j=1}^{2} \alpha_{j} y_{j} \boldsymbol{x}_{i}{ }^{T} \boldsymbol{x}_{j}-b} \end{aligned} vi​=j=3∑n​αj​yj​xi​Txj​=f(xi​)−j=1∑2​αj​yj​xi​Txj​−b​

最终目标函数变为:

W ( a 2 ) = α 1 + α 2 − 1 2 α 1 2 x 1 T x 1 − 1 2 α 2 2 x 2 T x 2 − y 1 y 2 α 1 α 2 x 1 T x 2 − y 1 α 1 v 1 − y 2 α 2 v 2 +  constant  \begin{aligned} W\left(a_{2}\right)=\alpha_{1}+& \alpha_{2}-\frac{1}{2} \alpha_{1}{ }^{2} \boldsymbol{x}_{1}{ }^{T} \boldsymbol{x}_{1}-\frac{1}{2} \alpha_{2}{ }^{2} \boldsymbol{x}_{2}{ }^{T} \boldsymbol{x}_{2}-y_{1} y_{2} \alpha_{1} \alpha_{2} \boldsymbol{x}_{1}{ }^{T} \boldsymbol{x}_{2}-y_{1} \alpha_{1} v_{1}-y_{2} \alpha_{2} v_{2} \\ &+\text { constant } \end{aligned} W(a2​)=α1​+​α2​−21​α1​2x1​Tx1​−21​α2​2x2​Tx2​−y1​y2​α1​α2​x1​Tx2​−y1​α1​v1​−y2​α2​v2​+ constant ​

不关心constant的部分，因为对于 α 1 \alpha 1 α1 和 α 2 \alpha 2 α2 来说，它们都是常数项，在求导的时候，直接变为 0 。对于这个目标函数，如果对其求导，还有个末知数 α 1 \alpha_1 α1​ ，所以要推导出 α 1 \alpha_1 α1​ 和 α 2 \alpha_2 α2​ 的关系，然后用 α 2 \alpha_2 α2​ 代替 α 1 \alpha_1 α1​ ，这样目标函数就剩一个末知数了，我们就可以求导了，推导出迭代公式。所以现在继续推导 α 1 \alpha _1 α1​ 和 α 2 \alpha _2 α2​ 的关系。注意第一个约束条件:

∑ i = 1 n α i y i = 0 \sum_{i=1}^{n} \alpha_{i} y_{i}=0 i=1∑n​αi​yi​=0

在求 α 1 \alpha _1 α1​ 和 α 2 \alpha _2 α2​ 的时候，可以将 α 3 , α 4 , … , α n \alpha _3, \alpha _4, \ldots, \alpha _n α3​,α4​,…,αn​ 和 y 3 , y 4 , … , y n y _3, y_ 4, \ldots, y _n y3​,y4​,…,yn​ 看作常数项。因此有:

α 1 y 1 + α 2 y 2 = B \alpha_{1} y_{1}+\alpha_{2} y_{2}=B α1​y1​+α2​y2​=B

不必关心常数B的大小，现在将上述等式两边同时乘以 y 1 y_1 y1​ ，得到 ( y 1 y 1 = 1 ) (y_ 1 y _1=1) (y1​y1​=1) :

α 1 = γ − s α 2 \alpha_{1}=\gamma-s \alpha_{2} α1​=γ−sα2​

其中 γ \gamma γ 为常数 B y 1 B y_1 By1​ ， s = y 1 y 2 s=y _1 y_ 2 s=y1​y2​ 。接下来，将得到的 α 1 \alpha _1 α1​ 带入 W ( α 2 ) W(\alpha _2) W(α2​) 公式得:

W ( a 2 ) = γ − s α 2 + α 2 − 1 2 ( γ − s α 2 ) 2 x 1 T x 1 − 1 2 α 2 2 x 2 T x 2 − s ( γ − s α 2 ) α 2 x 1 T x 2 − y 1 ( γ − s α 2 ) v 1 − y 2 α 2 v 2 +  constant  \begin{gathered} W\left(a_{2}\right)=\gamma-s \alpha_{2}+\alpha_{2}-\frac{1}{2}\left(\gamma-s \alpha_{2}\right)^{2} \boldsymbol{x}_{1}{ }^{T} \boldsymbol{x}_{1}-\frac{1}{2} \alpha_{2}{ }^{2} \boldsymbol{x}_{2}{ }^{T} \boldsymbol{x}_{2}-s\left(\gamma-s \alpha_{2}\right) \alpha_{2} \boldsymbol{x}_{1}{ }^{T} \boldsymbol{x}_{2} \\ -y_{1}\left(\gamma-s \alpha_{2}\right) v_{1}-y_{2} \alpha_{2} v_{2}+\text { constant } \end{gathered} W(a2​)=γ−sα2​+α2​−21​(γ−sα2​)2x1​Tx1​−21​α2​2x2​Tx2​−s(γ−sα2​)α2​x1​Tx2​−y1​(γ−sα2​)v1​−y2​α2​v2​+ constant ​

这样目标函数中就只剩下 α 2 \alpha _2 α2​ ， 对其求偏导 (注意: s = y 1 y 2 s=y _1 y_ 2 s=y1​y2​ ，所以s的平方为 1 ， y 1 1 ， y _1 1，y1​ 的平方和 y 2 y_2 y2​的平方均为 1 ) :

∂ W ( a 2 ) ∂ a 2 = − s + 1 + γ s x 1 T x 1 − α 2 x 1 T x 1 − α 2 x 2 T x 2 − γ s x 1 T x 2 + 2 α 2 x 1 T x 2 + y 2 v 1 − y 2 v 2 = 0 \begin{aligned} \frac{\partial W\left(a_{2}\right)}{\partial a_{2}} &=-s+1+\gamma s x_{1}^{T} x_{1}-\alpha_{2} x_{1}^{T} x_{1}-\alpha_{2} x_{2}^{T} x_{2} \\ &-\gamma s x_{1}^{T} x_{2}+2 \alpha_{2} x_{1}^{T} x_{2}+y_{2} v_{1}-y_{2} v_{2}=0 \end{aligned} ∂a2​∂W(a2​)​​=−s+1+γsx1T​x1​−α2​x1T​x1​−α2​x2T​x2​−γsx1T​x2​+2α2​x1T​x2​+y2​v1​−y2​v2​=0​

继续化简，将 s = y 1 y 2 s=y _1 y_ 2 s=y1​y2​ 带入方程得

α 2 n e w = y 2 ( y 2 − y 1 + y 1 γ ( x 1 T x 1 − x 1 T x 2 ) + v 1 − v 2 ) x 1 T x 1 + x 2 T x 2 − 2 x 1 T x 2 ③ \alpha_{2}^{n e w}=\frac{y_{2}\left(y_{2}-y_{1}+y_{1} \gamma\left(\boldsymbol{x}_{1}^{T} \boldsymbol{x}_{1}-\boldsymbol{x}_{1}^{T} \boldsymbol{x}_{2}\right)+v_{1}-v_{2}\right)}{\boldsymbol{x}_{1}^{T} \boldsymbol{x}_{1}+\boldsymbol{x}_{2}^{T} \boldsymbol{x}_{2}-2 \boldsymbol{x}_{1}^{T} \boldsymbol{x}_{2}}③ α2new​=x1T​x1​+x2T​x2​−2x1T​x2​y2​(y2​−y1​+y1​γ(x1T​x1​−x1T​x2​)+v1​−v2​)​③

令

E i = f ( x i ) − y i η = x 1 T x 1 + x 2 T x 2 − 2 x 1 T x 2 \begin{aligned} &E_{i}=f\left(x_{i}\right)-y_{i} \\ &\eta=x_{1}^{T} x_{1}+x_{2}^{T} x_{2}-2 x_{1}^{T} x_{2} \end{aligned} ​Ei​=f(xi​)−yi​η=x1T​x1​+x2T​x2​−2x1T​x2​​

E i E_i Ei​为误差项， η \eta η 为学习速率

再根据已知的公式:

γ = α 1 old  + s α 2 old  v j = ∑ i = 3 n α i y i x j T x i = f ( x j ) − ∑ i = 1 2 α i y i x j T x i − b \begin{aligned} &\gamma=\alpha_{1}{ }^{\text {old }}+\mathrm{s} \alpha_{2}{ }^{\text {old }} \\ &v_{j}=\sum_{i=3}^{n} \alpha_{i} y_{i} x_{j}{ }^{T} x_{i}=f\left(x_{j}\right)-\sum_{i=1}^{2} \alpha_{i} y_{i} x_{j}{ }^{T} x_{i}-b \end{aligned} ​γ=α1​old +sα2​old vj​=i=3∑n​αi​yi​xj​Txi​=f(xj​)−i=1∑2​αi​yi​xj​Txi​−b​

将以上两个式子代入式③得 α 2 n e w \alpha_2^{new} α2new​

推导过程：

在这里插入图片描述

α 2 new  = α 2 old  + y 2 ( E 1 − E 2 ) η \alpha_{2}^{\text {new }}=\alpha_{2}^{\text {old }}+\frac{y_{2}\left(E_{1}-E_{2}\right)}{\eta} α2new ​=α2old ​+ηy2​(E1​−E2​)​

这样，就得到了最终需要的迭代公式。这个是没有经过剪辑的解，需要考虑约束:

0 < α i < C 0<\alpha_{i}<C 0<αi​<C

根据之前推导的 α \alpha α 取值范围，得到最终的解析解为:

α 2 new  ,  clipped  = { H α 2 new  > H α 2 new  L ≤ α 2 new  ≤ H L α 2 new  < L \alpha_{2}^{\text {new }, \text { clipped }}=\left\{\begin{array}{lr} H & \alpha_{2}^{\text {new }}>H \\ \alpha_{2}^{\text {new }} & L \leq \alpha_{2}^{\text {new }} \leq H \\ L & \alpha_{2}^{\text {new }}<L \end{array}\right. α2new , clipped ​=⎩⎨⎧​Hα2new ​L​α2new ​>HL≤α2new ​≤Hα2new ​<L​

又因为:

α 1 old  = γ − s α 2 old  α 1 new  = γ − s α 2 new  ,  clipped  \begin{aligned} &\alpha_{1}^{\text {old }}=\gamma-s \alpha_{2}^{\text {old }} \\ &\alpha_{1}^{\text {new }}=\gamma-s \alpha_{2}^{\text {new }, \text { clipped }} \end{aligned} ​α1old ​=γ−sα2old ​α1new ​=γ−sα2new , clipped ​​

消去 γ \gamma γ 得:

α 1 new  = α 1 old  + y 1 y 2 ( α 2 old  − α 2 new, clipped  ) \alpha_{1}^{\text {new }}=\alpha_{1}^{\text {old }}+y_{1} y_{2}\left(\alpha_{2}^{\text {old }}-\alpha_{2}^{\text {new, clipped }}\right) α1new ​=α1old ​+y1​y2​(α2old ​−α2new, clipped ​)

这样，就知道了怎样计算 α 1 \alpha_ 1 α1​ 和 α 2 \alpha_ 2 α2​ ， 也就是如何对选择的 α \alpha α 进行更新。
当更新了 α 1 \alpha 1 α1 和 α 2 \alpha 2 α2 之后，需要重新计算阈值b，因为b关系到了 f ( x ) \mathrm{f}(\mathrm{x}) f(x) 的计算，也就关系到了误差E的计算。

根据 α \alpha α 的取值范围，去更正b的值，使间隔最大化。当 α 1 n e w \alpha_1^{new} α1new​在0和 C C C之间的时候，根据KKT 条件可知，这个点是支持向量上的点。因此，满足下列公式:

y 1 ( ω T x 1 + b ) = 1 y_{1}\left(\boldsymbol{\omega}^{T} \boldsymbol{x}_{\mathbf{1}}+b\right)=1 y1​(ωTx1​+b)=1

公式两边同时乘以 y 1 y_1 y1​ 得 ( y 1 y 1 = 1 ) (y _1 y _1=1) (y1​y1​=1) :

∑ i = 1 n α i y i x i x 1 + b = y 1 \sum_{i=1}^{n} \alpha_{i} y_{i} x_{i} x_{1}+b=y_{1} i=1∑n​αi​yi​xi​x1​+b=y1​

因为是根据 α 1 \alpha _1 α1​ 和 α 2 \alpha _2 α2​ 的值去更新 b \mathrm{b} b ，所以单独提出 i = 1 \mathrm{i}=1 i=1 和 i = 2 \mathrm{i}=2 i=2 的时候，整理可得:

b 1 n e w = y 1 − ∑ i = 3 n α i y i x i T x 1 − α 1 n e w y 1 x 1 T x 1 − α 2 new  y 2 x 2 T x 1 ④ b_{1}^{n e w}=y_{1}-\sum_{i=3}^{n} \alpha_{i} y_{i} \boldsymbol{x}_{i}{ }^{T} \boldsymbol{x}_{1}-\alpha_{1}{ }^{n e w} y_{1} \boldsymbol{x}_{1}{ }^{T} \boldsymbol{x}_{1}-\alpha_{2}{ }^{\text {new }} y_{2} \boldsymbol{x}_{2}{ }^{T} \boldsymbol{x}_{1}④ b1new​=y1​−i=3∑n​αi​yi​xi​Tx1​−α1​newy1​x1​Tx1​−α2​new y2​x2​Tx1​④

其中前两项为:

y 1 − ∑ i = 3 n α i y i x i T x 1 = − E 1 + α 1 old  y 1 x 1 T x 1 + α 2 old  y 2 x 2 T x 1 + b old  ⑤ y_{1}-\sum_{i=3}^{n} \alpha_{i} y_{i} x_{i}{ }^{T} x_{1}=-E_{1}+\alpha_{1}{ }^{\text {old }} y_{1} x_{1}{ }^{T} x_{1}+\alpha_{2}{ }^{\text {old }} y_{2}{\boldsymbol{x}}_{2}{ }^{T}{x}_{1}+b^{\text {old }}⑤ y1​−i=3∑n​αi​yi​xi​Tx1​=−E1​+α1​old y1​x1​Tx1​+α2​old y2​x2​Tx1​+bold ⑤

推导过程：

因为

f ( x i ) = ∑ j = 1 n α j y j x i T x j + b f\left(\boldsymbol{x}_{i}\right)=\sum_{j=1}^{n} \alpha_{j} y_{j} \boldsymbol{x}_{i}{ }^{T} \boldsymbol{x}_{j}+b f(xi​)=j=1∑n​αj​yj​xi​Txj​+b

E i = f ( x i ) − y i E_{i}=f\left(x_{i}\right)-y_{i} Ei​=f(xi​)−yi​

所以i=1时代入，可得

y 1 − ∑ i = 3 n α i y i x i T x 1 = − E 1 + α 1 old  y 1 x 1 T x 1 + α 2 old  y 2 x 2 T x 1 + b old  y_{1}-\sum_{i=3}^{n} \alpha_{i} y_{i} x_{i}{ }^{T} x_{1}=-E_{1}+\alpha_{1}{ }^{\text {old }} y_{1} x_{1}{ }^{T} x_{1}+\alpha_{2}{ }^{\text {old }} y_{2}{\boldsymbol{x}}_{2}{ }^{T}{x}_{1}+b^{\text {old }} y1​−i=3∑n​αi​yi​xi​Tx1​=−E1​+α1​old y1​x1​Tx1​+α2​old y2​x2​Tx1​+bold 

将上述两个公式④⑤，整理得:

b 1 new  = b old  − E 1 − y 1 ( α 1 new  − α 1 old  ) x 1 T x 1 − y 2 ( α 2 new  − α 2 old  ) x 2 T x 1 \begin{gathered} b_{1}^{\text {new }}=b^{\text {old }}-E_{1}-y_{1}\left(\alpha_{1}^{\text {new }}-\alpha_{1}^{\text {old }}\right) \boldsymbol{x}_{\mathbf{1}}^{T} \boldsymbol{x}_{\mathbf{1}} \\ -y_{2}\left(\alpha_{2}^{\text {new }}-\alpha_{2}^{\text {old }}\right) \boldsymbol{x}_{\mathbf{2}}^{\boldsymbol{T}} \boldsymbol{x}_{\mathbf{1}} \end{gathered} b1new ​=bold −E1​−y1​(α1new ​−α1old ​)x1T​x1​−y2​(α2new ​−α2old ​)x2T​x1​​

同理可得 b 2 n e w b_2^{new} b2new​为:

b 2 new  = b old  − E 2 − y 1 ( α 1 new  − α 1 old  ) x 1 T x 2 − y 2 ( α 2 new  − α 2 old  ) x 2 T x 2 \begin{gathered} b_{2}^{\text {new }}=b^{\text {old }}-E_{2}-y_{1}\left(\alpha_{1}^{\text {new }}-\alpha_{1}^{\text {old }}\right) \boldsymbol{x}_{\mathbf{1}}^{T} \boldsymbol{x}_{2} \\ -y_{2}\left(\alpha_{2}^{\text {new }}-\alpha_{2}^{\text {old }}\right) \boldsymbol{x}_{\mathbf{2}}^{T} \boldsymbol{x}_{2} \end{gathered} b2new ​=bold −E2​−y1​(α1new ​−α1old ​)x1T​x2​−y2​(α2new ​−α2old ​)x2T​x2​​

当 b 1 \mathrm{b} 1 b1 和 b 2 \mathrm{b} 2 b2 都有效(都属于 0 0 0到 C C C)的时候，它们是相等的，即:

b n e w = b 1 n e w = b 2 n e w b^{n e w}=b_{1}^{n e w}=b_{2}^{n e w} bnew=b1new​=b2new​

当两个乘子都在边界上，则b间值和KKT条件一致。当不满足的时候，SMO算法选择它们的中点作 为新的间值:

b = { b 1 , 0 < α 1 new  < C b 2 0 < α 2 new  < C ( b 1 + b 2 ) / 2  otherwise  b=\left\{\begin{array}{cc} b_{1}, & 0<\alpha_{1}^{\text {new }}<C \\ b_{2} & 0<\alpha_{2}^{\text {new }}<C \\ \left(b_{1}+b_{2}\right) / 2 & \text { otherwise } \end{array}\right. b=⎩⎨⎧​b1​,b2​(b1​+b2​)/2​0<α1new ​<C0<α2new ​<C otherwise ​

最后，更新所有的 α \alpha α 和 b \mathrm{b} b ，这样模型就出来了，从而即可求出我们的分类函数。

SMO算法求解步骤

  1. 计算误差：
    E i = f ( x i ) − y i = ∑ j = 1 n α j y j x i T x j + b − y i E_{i}=f\left(\boldsymbol{x}_{\boldsymbol{i}}\right)-\mathrm{y}_{i}=\sum_{j=1}^{n} \alpha_{j} y_{j} \boldsymbol{x}_{\boldsymbol{i}}^{\boldsymbol{T}} \boldsymbol{x}_{\boldsymbol{j}}+b-\mathrm{y}_{i} Ei​=f(xi​)−yi​=j=1∑n​αj​yj​xiT​xj​+b−yi​

  2. 计算上界 H H H和下界 L L L：
    { L = max ⁡ ( 0 , α j old  − α i old  ) , H = min ⁡ ( C , C + α j old  − α i old  )  if  y i ≠ y j L = max ⁡ ( 0 , α j old  + α i old  − C ) , H = min ⁡ ( C , α j old  + α i old  )  if  y i = y j \left\{\begin{array}{l} L=\max \left(0, \alpha_{j}^{\text {old }}-\alpha_{i}^{\text {old }}\right), H=\min \left(C, C+\alpha_{j}^{\text {old }}-\alpha_{i}^{\text {old }}\right) \text { if } \mathrm{y}_{i} \neq \mathrm{y}_{j} \\ L=\max \left(0, \alpha_{j}^{\text {old }}+\alpha_{i}^{\text {old }}-C\right), H=\min \left(C, \alpha_{j}^{\text {old }}+\alpha_{i}^{\text {old }}\right) \text { if } \mathrm{y}_{i} =\mathrm{y}_{j} \end{array}\right. {L=max(0,αjold ​−αiold ​),H=min(C,C+αjold ​−αiold ​) if yi​​=yj​L=max(0,αjold ​+αiold ​−C),H=min(C,αjold ​+αiold ​) if yi​=yj​​

  3. 计算 η \eta η:
    η = x i T x i + x j T x j − 2 x i T x j \eta=x_{i}^{T} x_{i}+x_{j}^{T} x_{j}-2 x_{i}^{T} x_{j} η=xiT​xi​+xjT​xj​−2xiT​xj​

    加个负号变换下形式
    η = − η = − ( x i T x i + x j T x j − 2 x i T x j ) = 2 x i T x j − x i T x i − x j T x j \eta=-\eta =-(x_{i}^{T} x_{i}+x_{j}^{T} x_{j}-2 x_{i}^{T} x_{j})=2 x_{i}^{T} x_{j}-x_{i}^{T} x_{i}-x_{j}^{T} x_{j} η=−η=−(xiT​xi​+xjT​xj​−2xiT​xj​)=2xiT​xj​−xiT​xi​−xjT​xj​

  4. 更新 α j \alpha_j αj​:
    α j new  = α j old  − y j ( E i − E j ) η \alpha_{j}^{\text {new }}=\alpha_{j}^{\text {old }}-\frac{y_{j}\left(E_{i}-E_{j}\right)}{\eta} αjnew ​=αjold ​−ηyj​(Ei​−Ej​)​

  5. 根据取值范围修剪 α j \alpha_j αj​ :
    α new, clipped  = { H  if  α 2 new  ≥ H α 2 new   if  L ≤ α 2 new  ≤ H L  if  α 2 new  ≤ L \alpha^{\text {new, clipped }}=\left\{\begin{array}{lr} H & \text { if } \alpha_{2}^{\text {new }} \geq H \\ \alpha_{2}^{\text {new }} & \text { if } L \leq \alpha_{2}^{\text {new }} \leq H \\ L & \text { if } \alpha_{2}^{\text {new }} \leq L \end{array}\right. αnew, clipped =⎩⎨⎧​Hα2new ​L​ if α2new ​≥H if L≤α2new ​≤H if α2new ​≤L​

  6. 更新 α i \alpha_i αi​:
    α i new  = α i old  + y i y j ( α j old  − α j new, clipped  ) \alpha_{i}^{\text {new }}=\alpha_{i}^{\text {old }}+y_{i} y_{j}\left(\alpha_{j}^{\text {old }}-\alpha_{j}^{\text {new, clipped }}\right) αinew ​=αiold ​+yi​yj​(αjold ​−αjnew, clipped ​)

  7. 更新 b 1 b_1 b1​和 b 2 b_2 b2​:
    b 1 new  = b old  − E i − y i ( α i new  − α i old  ) x i T x i − y j ( α j new  − α j old  ) x j T x i b 2 new  = b old  − E j − y i ( α i new  − α i old  ) x i T x j − y j ( α j new  − α j old  ) x j T x j \begin{aligned} b_{1}^{\text {new }}=& b^{\text {old }}-E_{i}-y_{i}\left(\alpha_{i}^{\text {new }}-\alpha_{i}^{\text {old }}\right) \boldsymbol{x}_{\boldsymbol{i}}^{T} \boldsymbol{x}_{i}-y_{j}\left(\alpha_{j}^{\text {new }}\right.\\ &\left.-\alpha_{j}^{\text {old }}\right) \boldsymbol{x}_{j}^{T} \boldsymbol{x}_{i} \\ b_{2}^{\text {new }}=& b^{\text {old }}-E_{j}-y_{i}\left(\alpha_{i}^{\text {new }}-\alpha_{i}^{\text {old }}\right) \boldsymbol{x}_{\boldsymbol{i}}^{T} \boldsymbol{x}_{j}-y_{j}\left(\alpha_{j}^{\text {new }}\right.\\ &\left.-\alpha_{j}^{\text {old }}\right) \boldsymbol{x}_{\boldsymbol{j}}^{\boldsymbol{T}} \boldsymbol{x}_{\boldsymbol{j}} \end{aligned} b1new ​=b2new ​=​bold −Ei​−yi​(αinew ​−αiold ​)xiT​xi​−yj​(αjnew ​−αjold ​)xjT​xi​bold −Ej​−yi​(αinew ​−αiold ​)xiT​xj​−yj​(αjnew ​−αjold ​)xjT​xj​​

  8. 根据 b 1 \mathrm{b}_1 b1​ 和 b 2 \mathrm{b}_2 b2​ 更新 b \mathrm{b} b :
    b = { b 1 0 < α 1 n e w < C b 2 0 < α 2 n e w < C b 1 + b 2 2  otherwise  b=\left\{\begin{array}{lc} b_{1} & 0<\alpha_{1}^{n e w}<C \\ b_{2} & 0<\alpha_{2}^{n e w}<C \\ \frac{b_{1}+b_{2}}{2} & \text { otherwise } \end{array}\right. b=⎩⎨⎧​b1​b2​2b1​+b2​​​0<α1new​<C0<α2new​<C otherwise ​

编程求解线性SVM

可视化数据集

import matplotlib.pyplot as plt
import numpy as np

#读取数据
def loadDataSet(fileName):
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines(): #逐行读取，滤除空格等
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]),float(lineArr[1])]) #添加数据
        labelMat.append(float(lineArr[2])) #添加标签
    return dataMat,labelMat

#数据可视化
def showDataSet(dataMat,labelMat):
    data_plus = []
    data_minus = []
    for i in range(len(dataMat)):
        if labelMat[i] > 0:
            data_plus.append(dataMat[i])
        else:
            data_minus.append(dataMat[i])
    data_plus_np = np.array(data_plus) #转换为numpy矩阵
    data_minus_np = np.array(data_minus)#转换为numpy矩阵
    plt.scatter(np.transpose(data_plus_np)[0],np.transpose(data_plus_np)[1]) #正样本
    plt.scatter(np.transpose(data_minus_np)[0],np.transpose(data_minus_np)[1]) #负样本
    plt.show()

dataMat,labelMat = loadDataSet('testSet.txt')
showDataSet(dataMat,labelMat)

png

这个数据集显然线性可分

应用简化版SMO算法处理小规模数据集

下面给出简化版SMO算法的实现
但执行速度慢。Platt SMO算法中的外循环确定要优化的最佳alpha对。而简化版却会跳过这一部 分, 首先在数据集上遍历每一个alpha, 然后在剩下的alpha集合中随机选择另一个alpha, 从而构建alpha对。这里有一点相当重要, 就是我们要同时改变两个alpha。之所以这样做是因为我们有 一个约束条件:
∑ α i ⋅  label  ( i ) = 0 \sum \alpha_{i} \cdot \text { label }^{(i)}=0 ∑αi​⋅ label (i)=0
由于改变一个alpha可能会导致该约束条件失效, 因此我们总是同时改变两个alpha。

为此, 我们将构建一个辅助函数, 用于在某个区间范围内随机选择一个整数。同时, 我们也需要另一个辅助函数, 用于在数值太大时对其进行调整

import random

def selectJrand(i,m):
    j=i
    while(j==i): #选择一个不等于i的j
        j = int(random.uniform(0,m))
    return j

def clipAlpha(aj,H,L):
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj

dataArr,labelArr  =loadDataSet('testSet.txt')
labelArr

[-1.0,
 -1.0,
 1.0,
 -1.0,
 1.0,
 1.0,
 1.0,
 -1.0,
 -1.0,
 -1.0,
 -1.0,
 -1.0,
 -1.0,
 1.0,
 -1.0,
 1.0,
 1.0,
 -1.0,
 1.0,
 -1.0,
 -1.0,
 -1.0,
 1.0,
 -1.0,
 -1.0,
 1.0,
 1.0,
 -1.0,
 -1.0,
 -1.0,
 -1.0,
 1.0,
 1.0,
 1.0,
 1.0,
 -1.0,
 1.0,
 -1.0,
 -1.0,
 1.0,
 -1.0,
 -1.0,
 -1.0,
 -1.0,
 1.0,
 1.0,
 1.0,
 1.0,
 1.0,
 -1.0,
 1.0,
 1.0,
 -1.0,
 -1.0,
 1.0,
 1.0,
 -1.0,
 1.0,
 -1.0,
 -1.0,
 -1.0,
 -1.0,
 1.0,
 -1.0,
 1.0,
 -1.0,
 -1.0,
 1.0,
 1.0,
 1.0,
 -1.0,
 1.0,
 1.0,
 -1.0,
 -1.0,
 1.0,
 -1.0,
 1.0,
 1.0,
 1.0,
 1.0,
 1.0,
 1.0,
 1.0,
 -1.0,
 -1.0,
 -1.0,
 -1.0,
 1.0,
 -1.0,
 1.0,
 1.0,
 1.0,
 -1.0,
 -1.0,
 -1.0,
 -1.0,
 -1.0,
 -1.0,
 -1.0]

data = np.mat(dataArr)
data[2,:]

matrix([[ 7.55151, -1.58003]])

可以看出来，这里使用的类别标签是-1和1

SMO算法的伪代码：

创建一个alpha向量并将其初始化为 0 向量 
当迭代次数小于最大迭代次数时 (外循环) 
    对数据集中的每个数据向量 (内循环):
    如果该数据向量可以被优化:
        随机选择另外一个数据向量
        同时优化这两个向量
        如果两个向量都不能被优化, 退出内循环
如果所有向量都没被优化, 增加迭代数目, 继续下一次循环


#简化版SMO算法
def smoSimple(dataMatIn,classLabels,C,toler,maxIter):
    dataMatrix = np.mat(dataMatIn); labelMat = np.mat(classLabels).transpose()
    b = 0; m,n = np.shape(dataMatrix)
    alphas = np.mat(np.zeros((m,1)))#初始化alpha参数，设置为0
    iterSmo = 0 #初始化迭代次数
    while(iterSmo < maxIter):
        alphaPairsChanged = 0#用于记录alpha是否已经进行优化
        #步骤1. 计算误差Ei
        for i in range(m):
            fXi = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
            Ei = fXi - float(labelMat[i])
            if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > -toler) and (alphas[i] > 0)):
                j = selectJrand(i,m)
                #步骤1. 计算误差Ej
                fXj = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
                Ej = fXj - float(labelMat[j])
                #保存更新前的alpha值，使用浅拷贝
                alphaIold = alphas[i].copy()
                alphaJold = alphas[j].copy()
                #步骤2：计算上界H和下界L
                if (labelMat[i] != labelMat[j]):
                    L = max(0,alphas[j] - alphas[i])
                    H = min(C,C + alphas[j] - alphas[i])
                else:
                    L = max(0,alphas[j] + alphas[i] - C)
                    H = min(C,alphas[j] + alphas[i])
                if L==H: print("L==H"); continue
                #步骤3：计算eta
                eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
                if eta >=0 : print("eta>=0");continue
                #步骤4：更新alpha_j
                alphas[j] -= labelMat[j]*(Ei-Ej)/eta
                #步骤5：修剪alpha_j
                alphas[j] = clipAlpha(alphas[j],H,L)
                if (abs(alphas[j] - alphaJold) < 0.00001) : print("j not moving enough") ; continue
                #步骤6：更新alpha_i
                alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])
                #步骤7：更新b_1和b_2
                b1 = b - Ei - labelMat[i]*(alphas[i] - alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T \
                - labelMat[j]*(alphas[j] - alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
                b2 = b - Ej - labelMat[i]*(alphas[i] - alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T \
                - labelMat[j]*(alphas[j] - alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
                #步骤8：根据b_1和b_2更新b
                if (0 < alphas[i]) and (C > alphas[i]) :
                    b = b1
                elif (0 < alphas[j]) and (C > alphas[j]):
                    b = b2
                else:
                    b = (b1 + b2)/2.0
                #统计优化次数
                #如果程序执行到for循环的最后一行都不执行continue语句，那么就已经成功地改变了一对alpha，同时可以增加alphaPairsChanged的值
                alphaPairsChanged += 1
                #打印统计信息
                print("第%d次迭代 样本:%d, alpha优化次数:%d" % (iterSmo,i,alphaPairsChanged))
        #更新迭代次数
        #在for循环之外，需要检查alpha值是否做了更新，如果有更新则将iterSmo设为0后继续运行程序。只有在所有数据集上遍历maxIter次，且不再发生任何alpha修改之后，程序才会停止并退出while循环
        if (alphaPairsChanged == 0): iterSmo += 1
        else:
            iterSmo = 0
        print("迭代次数：%d" % iterSmo)
    return b,alphas

b,alphas = smoSimple(dataArr,labelArr,0.6,0.001,500)

L==H
第0次迭代 样本:1, alpha优化次数:1
第0次迭代 样本:3, alpha优化次数:2
第0次迭代 样本:5, alpha优化次数:3
L==H
第0次迭代 样本:8, alpha优化次数:4
L==H
j not moving enough
j not moving enough
L==H
L==H
j not moving enough
L==H
第0次迭代 样本:30, alpha优化次数:5
第0次迭代 样本:31, alpha优化次数:6
L==H
L==H
第0次迭代 样本:54, alpha优化次数:7
L==H
L==H
第0次迭代 样本:71, alpha优化次数:8
L==H
L==H
L==H
第0次迭代 样本:79, alpha优化次数:9
L==H
第0次迭代 样本:92, alpha优化次数:10
j not moving enough
L==H
迭代次数：0
第0次迭代 样本:1, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
L==H
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
L==H
L==H
j not moving enough
j not moving enough
第0次迭代 样本:37, alpha优化次数:2
第0次迭代 样本:39, alpha优化次数:3
第0次迭代 样本:52, alpha优化次数:4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第0次迭代 样本:71, alpha优化次数:5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
第0次迭代 样本:8, alpha优化次数:1
L==H
j not moving enough
第0次迭代 样本:23, alpha优化次数:2
L==H
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
第0次迭代 样本:39, alpha优化次数:3
L==H
j not moving enough
第0次迭代 样本:52, alpha优化次数:4
j not moving enough
第0次迭代 样本:55, alpha优化次数:5
L==H
L==H
L==H
L==H
L==H
j not moving enough
第0次迭代 样本:79, alpha优化次数:6
第0次迭代 样本:92, alpha优化次数:7
迭代次数：0
j not moving enough
L==H
j not moving enough
j not moving enough
L==H
j not moving enough
第0次迭代 样本:23, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
L==H
第0次迭代 样本:51, alpha优化次数:2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
第0次迭代 样本:69, alpha优化次数:3
L==H
j not moving enough
第0次迭代 样本:94, alpha优化次数:4
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第0次迭代 样本:69, alpha优化次数:1
L==H
第0次迭代 样本:78, alpha优化次数:2
j not moving enough
L==H
L==H
j not moving enough
j not moving enough
迭代次数：0
L==H
j not moving enough
j not moving enough
L==H
L==H
j not moving enough
j not moving enough
第0次迭代 样本:24, alpha优化次数:1
j not moving enough
j not moving enough
L==H
j not moving enough
第0次迭代 样本:34, alpha优化次数:2
j not moving enough
j not moving enough
L==H
第0次迭代 样本:46, alpha优化次数:3
第0次迭代 样本:47, alpha优化次数:4
j not moving enough
j not moving enough
第0次迭代 样本:54, alpha优化次数:5
第0次迭代 样本:55, alpha优化次数:6
j not moving enough
j not moving enough
第0次迭代 样本:96, alpha优化次数:7
j not moving enough
迭代次数：0
j not moving enough
第0次迭代 样本:6, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
L==H
L==H
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第0次迭代 样本:47, alpha优化次数:2
第0次迭代 样本:51, alpha优化次数:3
第0次迭代 样本:52, alpha优化次数:4
j not moving enough
第0次迭代 样本:55, alpha优化次数:5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
第0次迭代 样本:17, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第0次迭代 样本:94, alpha优化次数:2
j not moving enough
迭代次数：0
j not moving enough
L==H
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第0次迭代 样本:46, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
第0次迭代 样本:8, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第0次迭代 样本:39, alpha优化次数:2
第0次迭代 样本:46, alpha优化次数:3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第0次迭代 样本:94, alpha优化次数:4
L==H
迭代次数：0
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
第0次迭代 样本:46, alpha优化次数:1
j not moving enough
j not moving enough
第0次迭代 样本:55, alpha优化次数:2
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第0次迭代 样本:46, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
L==H
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第1次迭代 样本:23, alpha优化次数:1
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
第0次迭代 样本:8, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
第0次迭代 样本:46, alpha优化次数:1
j not moving enough
第0次迭代 样本:54, alpha优化次数:2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第1次迭代 样本:76, alpha优化次数:1
j not moving enough
j not moving enough
第1次迭代 样本:96, alpha优化次数:2
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
L==H
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
第0次迭代 样本:54, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第0次迭代 样本:29, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第5次迭代 样本:52, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第9次迭代 样本:96, alpha优化次数:1
j not moving enough
迭代次数：0
j not moving enough
L==H
L==H
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
迭代次数：1
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
迭代次数：2
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
第2次迭代 样本:29, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
第0次迭代 样本:0, alpha优化次数:1
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
第0次迭代 样本:55, alpha优化次数:2
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
第1次迭代 样本:23, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
第0次迭代 样本:23, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第1次迭代 样本:52, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
第9次迭代 样本:8, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
第0次迭代 样本:17, alpha优化次数:1
第0次迭代 样本:23, alpha优化次数:2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
第0次迭代 样本:10, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
第8次迭代 样本:17, alpha优化次数:1
j not moving enough
j not moving enough
第8次迭代 样本:52, alpha优化次数:2
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第5次迭代 样本:52, alpha优化次数:1
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第2次迭代 样本:55, alpha优化次数:1
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
第3次迭代 样本:23, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
第3次迭代 样本:55, alpha优化次数:2
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
第4次迭代 样本:23, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
第4次迭代 样本:55, alpha优化次数:2
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：10
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：11
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：12
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：13
j not moving enough
j not moving enough
第13次迭代 样本:52, alpha优化次数:1
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：10
j not moving enough
j not moving enough
j not moving enough
第10次迭代 样本:54, alpha优化次数:1
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：10
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：11
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：12
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：13
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：14
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：15
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：16
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：17
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：18
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：19
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：20
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：21
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：22
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：23
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：24
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：25
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：26
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：27
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：28
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：29
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：30
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：31
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：32
j not moving enough
j not moving enough
j not moving enough
第32次迭代 样本:54, alpha优化次数:1
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
第4次迭代 样本:52, alpha优化次数:1
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
第0次迭代 样本:52, alpha优化次数:1
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：10
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：11
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：12
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：13
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：14
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：15
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：16
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：17
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：18
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：19
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：20
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：21
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：22
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：23
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：24
j not moving enough
第24次迭代 样本:23, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
第2次迭代 样本:52, alpha优化次数:1
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
第0次迭代 样本:29, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：10
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：11
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：12
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第12次迭代 样本:55, alpha优化次数:1
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：10
j not moving enough
j not moving enough
第10次迭代 样本:29, alpha优化次数:1
第10次迭代 样本:52, alpha优化次数:2
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第3次迭代 样本:54, alpha优化次数:1
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：10
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：11
j not moving enough
j not moving enough
j not moving enough
第11次迭代 样本:52, alpha优化次数:1
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第5次迭代 样本:54, alpha优化次数:1
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
第2次迭代 样本:29, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：10
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：11
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：12
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：13
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：14
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：15
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第15次迭代 样本:55, alpha优化次数:1
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第0次迭代 样本:55, alpha优化次数:1
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
第2次迭代 样本:29, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
第4次迭代 样本:17, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
第4次迭代 样本:29, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第1次迭代 样本:55, alpha优化次数:1
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
第5次迭代 样本:17, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
第0次迭代 样本:17, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
第1次迭代 样本:52, alpha优化次数:1
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：10
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：11
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：12
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：13
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：14
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：15
第15次迭代 样本:17, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：10
第10次迭代 样本:17, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
第4次迭代 样本:54, alpha优化次数:1
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
第5次迭代 样本:52, alpha优化次数:1
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
L==H
j not moving enough
第0次迭代 样本:52, alpha优化次数:1
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
第1次迭代 样本:17, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
第1次迭代 样本:55, alpha优化次数:2
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
L==H
j not moving enough
j not moving enough
第1次迭代 样本:54, alpha优化次数:1
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
第1次迭代 样本:29, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
第5次迭代 样本:52, alpha优化次数:1
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
第3次迭代 样本:17, alpha优化次数:1
L==H
j not moving enough
L==H
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
L==H
j not moving enough
L==H
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
第6次迭代 样本:29, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
第3次迭代 样本:55, alpha优化次数:1
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
第3次迭代 样本:52, alpha优化次数:1
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：10
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：11
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：12
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：13
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：14
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：15
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：16
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：17
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：18
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：19
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：20
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：21
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：22
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：23
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：24
j not moving enough
j not moving enough
第24次迭代 样本:54, alpha优化次数:1
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：10
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：11
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：12
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：13
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：14
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：15
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：16
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：17
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：18
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：19
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：20
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：21
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：22
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：23
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：24
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：25
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：26
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：27
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：28
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：29
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：30
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：31
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：32
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：33
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：34
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：35
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：36
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：37
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：38
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：39
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：40
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：41
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：42
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：43
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：44
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：45
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：46
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：47
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：48
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：49
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：50
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：51
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：52
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：53
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：54
第54次迭代 样本:17, alpha优化次数:1
j not moving enough
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
第8次迭代 样本:29, alpha优化次数:1
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：10
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：11
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：12
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：13
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：14
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：15
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：16
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：17
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：18
j not moving enough
第18次迭代 样本:29, alpha优化次数:1
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：10
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：11
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：12
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：13
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：14
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：15
j not moving enough
j not moving enough
第15次迭代 样本:54, alpha优化次数:1
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
第1次迭代 样本:54, alpha优化次数:1
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
第2次迭代 样本:29, alpha优化次数:1
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
第6次迭代 样本:29, alpha优化次数:1
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
第5次迭代 样本:17, alpha优化次数:1
j not moving enough
j not moving enough
第5次迭代 样本:55, alpha优化次数:2
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
迭代次数：10
j not moving enough
j not moving enough
j not moving enough
迭代次数：11
j not moving enough
j not moving enough
j not moving enough
迭代次数：12
j not moving enough
j not moving enough
j not moving enough
迭代次数：13
j not moving enough
j not moving enough
j not moving enough
迭代次数：14
j not moving enough
j not moving enough
j not moving enough
迭代次数：15
j not moving enough
j not moving enough
j not moving enough
迭代次数：16
j not moving enough
j not moving enough
j not moving enough
迭代次数：17
j not moving enough
j not moving enough
j not moving enough
迭代次数：18
j not moving enough
j not moving enough
j not moving enough
迭代次数：19
j not moving enough
j not moving enough
j not moving enough
迭代次数：20
j not moving enough
j not moving enough
j not moving enough
迭代次数：21
j not moving enough
j not moving enough
j not moving enough
迭代次数：22
j not moving enough
j not moving enough
j not moving enough
迭代次数：23
j not moving enough
j not moving enough
j not moving enough
迭代次数：24
j not moving enough
j not moving enough
j not moving enough
迭代次数：25
j not moving enough
j not moving enough
j not moving enough
迭代次数：26
j not moving enough
j not moving enough
j not moving enough
迭代次数：27
j not moving enough
j not moving enough
j not moving enough
迭代次数：28
j not moving enough
j not moving enough
j not moving enough
迭代次数：29
j not moving enough
j not moving enough
j not moving enough
迭代次数：30
j not moving enough
第30次迭代 样本:29, alpha优化次数:1
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
迭代次数：10
j not moving enough
j not moving enough
j not moving enough
迭代次数：11
第11次迭代 样本:17, alpha优化次数:1
j not moving enough
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
迭代次数：10
j not moving enough
j not moving enough
j not moving enough
迭代次数：11
j not moving enough
j not moving enough
j not moving enough
迭代次数：12
j not moving enough
j not moving enough
j not moving enough
迭代次数：13
j not moving enough
j not moving enough
j not moving enough
迭代次数：14
j not moving enough
j not moving enough
j not moving enough
迭代次数：15
j not moving enough
j not moving enough
第15次迭代 样本:55, alpha优化次数:1
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
迭代次数：10
j not moving enough
j not moving enough
j not moving enough
迭代次数：11
j not moving enough
j not moving enough
j not moving enough
迭代次数：12
j not moving enough
j not moving enough
j not moving enough
迭代次数：13
j not moving enough
j not moving enough
j not moving enough
迭代次数：14
j not moving enough
j not moving enough
j not moving enough
迭代次数：15
j not moving enough
j not moving enough
j not moving enough
迭代次数：16
j not moving enough
j not moving enough
j not moving enough
迭代次数：17
j not moving enough
j not moving enough
j not moving enough
迭代次数：18
j not moving enough
j not moving enough
j not moving enough
迭代次数：19
j not moving enough
j not moving enough
j not moving enough
迭代次数：20
j not moving enough
j not moving enough
j not moving enough
迭代次数：21
j not moving enough
j not moving enough
j not moving enough
迭代次数：22
j not moving enough
j not moving enough
j not moving enough
迭代次数：23
j not moving enough
j not moving enough
j not moving enough
迭代次数：24
j not moving enough
j not moving enough
j not moving enough
迭代次数：25
j not moving enough
j not moving enough
j not moving enough
迭代次数：26
j not moving enough
j not moving enough
j not moving enough
迭代次数：27
j not moving enough
j not moving enough
j not moving enough
迭代次数：28
j not moving enough
j not moving enough
j not moving enough
迭代次数：29
j not moving enough
j not moving enough
j not moving enough
迭代次数：30
j not moving enough
第30次迭代 样本:29, alpha优化次数:1
j not moving enough
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
迭代次数：10
j not moving enough
j not moving enough
j not moving enough
迭代次数：11
j not moving enough
j not moving enough
j not moving enough
迭代次数：12
j not moving enough
j not moving enough
j not moving enough
迭代次数：13
j not moving enough
j not moving enough
j not moving enough
迭代次数：14
j not moving enough
j not moving enough
j not moving enough
迭代次数：15
j not moving enough
j not moving enough
j not moving enough
迭代次数：16
j not moving enough
j not moving enough
j not moving enough
迭代次数：17
j not moving enough
j not moving enough
j not moving enough
迭代次数：18
j not moving enough
j not moving enough
j not moving enough
迭代次数：19
j not moving enough
j not moving enough
j not moving enough
迭代次数：20
j not moving enough
j not moving enough
j not moving enough
迭代次数：21
j not moving enough
j not moving enough
j not moving enough
迭代次数：22
j not moving enough
j not moving enough
j not moving enough
迭代次数：23
j not moving enough
j not moving enough
j not moving enough
迭代次数：24
j not moving enough
j not moving enough
j not moving enough
迭代次数：25
j not moving enough
j not moving enough
j not moving enough
迭代次数：26
j not moving enough
j not moving enough
j not moving enough
迭代次数：27
j not moving enough
j not moving enough
j not moving enough
迭代次数：28
j not moving enough
j not moving enough
j not moving enough
迭代次数：29
j not moving enough
j not moving enough
j not moving enough
迭代次数：30
j not moving enough
j not moving enough
第30次迭代 样本:55, alpha优化次数:1
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
迭代次数：10
j not moving enough
j not moving enough
j not moving enough
迭代次数：11
j not moving enough
j not moving enough
j not moving enough
迭代次数：12
j not moving enough
j not moving enough
j not moving enough
迭代次数：13
j not moving enough
j not moving enough
j not moving enough
迭代次数：14
j not moving enough
j not moving enough
j not moving enough
迭代次数：15
j not moving enough
j not moving enough
j not moving enough
迭代次数：16
j not moving enough
j not moving enough
j not moving enough
迭代次数：17
j not moving enough
j not moving enough
j not moving enough
迭代次数：18
j not moving enough
j not moving enough
j not moving enough
迭代次数：19
j not moving enough
j not moving enough
j not moving enough
迭代次数：20
j not moving enough
j not moving enough
j not moving enough
迭代次数：21
j not moving enough
j not moving enough
j not moving enough
迭代次数：22
j not moving enough
j not moving enough
j not moving enough
迭代次数：23
j not moving enough
j not moving enough
j not moving enough
迭代次数：24
j not moving enough
j not moving enough
j not moving enough
迭代次数：25
j not moving enough
j not moving enough
j not moving enough
迭代次数：26
j not moving enough
j not moving enough
j not moving enough
迭代次数：27
j not moving enough
j not moving enough
第27次迭代 样本:55, alpha优化次数:1
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
第7次迭代 样本:55, alpha优化次数:1
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
迭代次数：10
j not moving enough
j not moving enough
j not moving enough
迭代次数：11
j not moving enough
j not moving enough
j not moving enough
迭代次数：12
j not moving enough
j not moving enough
j not moving enough
迭代次数：13
j not moving enough
j not moving enough
j not moving enough
迭代次数：14
j not moving enough
j not moving enough
j not moving enough
迭代次数：15
j not moving enough
j not moving enough
j not moving enough
迭代次数：16
j not moving enough
j not moving enough
j not moving enough
迭代次数：17
j not moving enough
j not moving enough
j not moving enough
迭代次数：18
j not moving enough
j not moving enough
j not moving enough
迭代次数：19
j not moving enough
j not moving enough
j not moving enough
迭代次数：20
j not moving enough
j not moving enough
j not moving enough
迭代次数：21
j not moving enough
j not moving enough
j not moving enough
迭代次数：22
j not moving enough
j not moving enough
j not moving enough
迭代次数：23
j not moving enough
j not moving enough
j not moving enough
迭代次数：24
j not moving enough
j not moving enough
j not moving enough
迭代次数：25
j not moving enough
j not moving enough
j not moving enough
迭代次数：26
j not moving enough
j not moving enough
j not moving enough
迭代次数：27
j not moving enough
j not moving enough
j not moving enough
迭代次数：28
j not moving enough
j not moving enough
j not moving enough
迭代次数：29
j not moving enough
j not moving enough
j not moving enough
迭代次数：30
j not moving enough
j not moving enough
j not moving enough
迭代次数：31
j not moving enough
j not moving enough
j not moving enough
迭代次数：32
j not moving enough
j not moving enough
j not moving enough
迭代次数：33
j not moving enough
j not moving enough
j not moving enough
迭代次数：34
j not moving enough
j not moving enough
j not moving enough
迭代次数：35
j not moving enough
j not moving enough
j not moving enough
迭代次数：36
j not moving enough
j not moving enough
j not moving enough
迭代次数：37
j not moving enough
j not moving enough
j not moving enough
迭代次数：38
j not moving enough
j not moving enough
j not moving enough
迭代次数：39
j not moving enough
j not moving enough
j not moving enough
迭代次数：40
j not moving enough
j not moving enough
j not moving enough
迭代次数：41
j not moving enough
j not moving enough
j not moving enough
迭代次数：42
j not moving enough
j not moving enough
j not moving enough
迭代次数：43
j not moving enough
j not moving enough
j not moving enough
迭代次数：44
j not moving enough
j not moving enough
j not moving enough
迭代次数：45
j not moving enough
j not moving enough
j not moving enough
迭代次数：46
j not moving enough
j not moving enough
j not moving enough
迭代次数：47
j not moving enough
j not moving enough
j not moving enough
迭代次数：48
j not moving enough
j not moving enough
j not moving enough
迭代次数：49
j not moving enough
j not moving enough
j not moving enough
迭代次数：50
j not moving enough
j not moving enough
j not moving enough
迭代次数：51
j not moving enough
j not moving enough
j not moving enough
迭代次数：52
j not moving enough
j not moving enough
j not moving enough
迭代次数：53
j not moving enough
j not moving enough
j not moving enough
迭代次数：54
j not moving enough
j not moving enough
j not moving enough
迭代次数：55
j not moving enough
j not moving enough
j not moving enough
迭代次数：56
j not moving enough
j not moving enough
j not moving enough
迭代次数：57
j not moving enough
j not moving enough
j not moving enough
迭代次数：58
j not moving enough
j not moving enough
j not moving enough
迭代次数：59
j not moving enough
j not moving enough
j not moving enough
迭代次数：60
j not moving enough
j not moving enough
j not moving enough
迭代次数：61
j not moving enough
j not moving enough
j not moving enough
迭代次数：62
j not moving enough
j not moving enough
j not moving enough
迭代次数：63
j not moving enough
j not moving enough
j not moving enough
迭代次数：64
j not moving enough
j not moving enough
j not moving enough
迭代次数：65
j not moving enough
j not moving enough
j not moving enough
迭代次数：66
j not moving enough
j not moving enough
j not moving enough
迭代次数：67
j not moving enough
j not moving enough
第67次迭代 样本:55, alpha优化次数:1
迭代次数：0
j not moving enough
j not moving enough
j not moving enough
迭代次数：1
j not moving enough
j not moving enough
j not moving enough
迭代次数：2
j not moving enough
j not moving enough
j not moving enough
迭代次数：3
j not moving enough
j not moving enough
j not moving enough
迭代次数：4
j not moving enough
j not moving enough
j not moving enough
迭代次数：5
j not moving enough
j not moving enough
j not moving enough
迭代次数：6
j not moving enough
j not moving enough
j not moving enough
迭代次数：7
j not moving enough
j not moving enough
j not moving enough
迭代次数：8
j not moving enough
j not moving enough
j not moving enough
迭代次数：9
j not moving enough
j not moving enough
j not moving enough
迭代次数：10
j not moving enough
j not moving enough
j not moving enough
迭代次数：11
j not moving enough
j not moving enough
j not moving enough
迭代次数：12
j not moving enough
j not moving enough
j not moving enough
迭代次数：13
j not moving enough
j not moving enough
j not moving enough
迭代次数：14
j not moving enough
j not moving enough
j not moving enough
迭代次数：15
j not moving enough
j not moving enough
j not moving enough
迭代次数：16
j not moving enough
j not moving enough
j not moving enough
迭代次数：17
j not moving enough
j not moving enough
j not moving enough
迭代次数：18
j not moving enough
j not moving enough
j not moving enough
迭代次数：19
j not moving enough
j not moving enough
j not moving enough
迭代次数：20
j not moving enough
j not moving enough
j not moving enough
迭代次数：21
j not moving enough
j not moving enough
j not moving enough
迭代次数：22
j not moving enough
j not moving enough
j not moving enough
迭代次数：23
j not moving enough
j not moving enough
j not moving enough
迭代次数：24
j not moving enough
j not moving enough
j not moving enough
迭代次数：25
j not moving enough
j not moving enough
j not moving enough
迭代次数：26
j not moving enough
j not moving enough
j not moving enough
迭代次数：27
j not moving enough
j not moving enough
j not moving enough
迭代次数：28
j not moving enough
j not moving enough
j not moving enough
迭代次数：29
j not moving enough
j not moving enough
j not moving enough
迭代次数：30
j not moving enough
j not moving enough
j not moving enough
迭代次数：31
j not moving enough
j not moving enough
j not moving enough
迭代次数：32
j not moving enough
j not moving enough
j not moving enough
迭代次数：33
j not moving enough
j not moving enough
j not moving enough
迭代次数：34
j not moving enough
j not moving enough
j not moving enough
迭代次数：35
j not moving enough
j not moving enough
j not moving enough
迭代次数：36
j not moving enough
j not moving enough
j not moving enough
迭代次数：37
j not moving enough
j not moving enough
j not moving enough
迭代次数：38
j not moving enough
j not moving enough
j not moving enough
迭代次数：39
j not moving enough
j not moving enough
j not moving enough
迭代次数：40
j not moving enough
j not moving enough
j not moving enough
迭代次数：41
j not moving enough
j not moving enough
j not moving enough
迭代次数：42
j not moving enough
j not moving enough
j not moving enough
迭代次数：43
j not moving enough
j not moving enough
j not moving enough
迭代次数：44
j not moving enough
j not moving enough
j not moving enough
迭代次数：45
j not moving enough
j not moving enough
j not moving enough
迭代次数：46
j not moving enough
j not moving enough
j not moving enough
迭代次数：47
j not moving enough
j not moving enough
j not moving enough
迭代次数：48
j not moving enough
j not moving enough
j not moving enough
迭代次数：49
j not moving enough
j not moving enough
j not moving enough
迭代次数：50
j not moving enough
j not moving enough
j not moving enough
迭代次数：51
j not moving enough
j not moving enough
j not moving enough
迭代次数：52
j not moving enough
j not moving enough
j not moving enough
迭代次数：53
j not moving enough
j not moving enough
j not moving enough
迭代次数：54
j not moving enough
j not moving enough
j not moving enough
迭代次数：55
j not moving enough
j not moving enough
j not moving enough
迭代次数：56
j not moving enough
j not moving enough
j not moving enough
迭代次数：57
j not moving enough
j not moving enough
j not moving enough
迭代次数：58
j not moving enough
j not moving enough
j not moving enough
迭代次数：59
j not moving enough
j not moving enough
j not moving enough
迭代次数：60
j not moving enough
j not moving enough
j not moving enough
迭代次数：61
j not moving enough
j not moving enough
j not moving enough
迭代次数：62
j not moving enough
j not moving enough
j not moving enough
迭代次数：63
j not moving enough
j not moving enough
j not moving enough
迭代次数：64
j not moving enough
j not moving enough
j not moving enough
迭代次数：65
j not moving enough
j not moving enough
j not moving enough
迭代次数：66
j not moving enough
j not moving enough
j not moving enough
迭代次数：67
j not moving enough
j not moving enough
j not moving enough
迭代次数：68
j not moving enough
j not moving enough
j not moving enough
迭代次数：69
j not moving enough
j not moving enough
j not moving enough
迭代次数：70
j not moving enough
j not moving enough
j not moving enough
迭代次数：71
j not moving enough
j not moving enough
j not moving enough
迭代次数：72
j not moving enough
j not moving enough
j not moving enough
迭代次数：73
j not moving enough
j not moving enough
j not moving enough
迭代次数：74
j not moving enough
j not moving enough
j not moving enough
迭代次数：75
j not moving enough
j not moving enough
j not moving enough
迭代次数：76
j not moving enough
j not moving enough
j not moving enough
迭代次数：77
j not moving enough
j not moving enough
j not moving enough
迭代次数：78
j not moving enough
j not moving enough
j not moving enough
迭代次数：79
j not moving enough
j not moving enough
j not moving enough
迭代次数：80
j not moving enough
j not moving enough
j not moving enough
迭代次数：81
j not moving enough
j not moving enough
j not moving enough
迭代次数：82
j not moving enough
j not moving enough
j not moving enough
迭代次数：83
j not moving enough
j not moving enough
j not moving enough
迭代次数：84
j not moving enough
j not moving enough
j not moving enough
迭代次数：85
j not moving enough
j not moving enough
j not moving enough
迭代次数：86
j not moving enough
j not moving enough
j not moving enough
迭代次数：87
j not moving enough
j not moving enough
j not moving enough
迭代次数：88
j not moving enough
j not moving enough
j not moving enough
迭代次数：89
j not moving enough
j not moving enough
j not moving enough
迭代次数：90
j not moving enough
j not moving enough
j not moving enough
迭代次数：91
j not moving enough
j not moving enough
j not moving enough
迭代次数：92
j not moving enough
j not moving enough
j not moving enough
迭代次数：93
j not moving enough
j not moving enough
j not moving enough
迭代次数：94
j not moving enough
j not moving enough
j not moving enough
迭代次数：95
j not moving enough
j not moving enough
j not moving enough
迭代次数：96
j not moving enough
j not moving enough
j not moving enough
迭代次数：97
j not moving enough
j not moving enough
j not moving enough
迭代次数：98
j not moving enough
j not moving enough
j not moving enough
迭代次数：99
j not moving enough
j not moving enough
j not moving enough
迭代次数：100
j not moving enough
j not moving enough
j not moving enough
迭代次数：101
j not moving enough
j not moving enough
j not moving enough
迭代次数：102
j not moving enough
j not moving enough
j not moving enough
迭代次数：103
j not moving enough
j not moving enough
j not moving enough
迭代次数：104
j not moving enough
j not moving enough
j not moving enough
迭代次数：105
j not moving enough
j not moving enough
j not moving enough
迭代次数：106
j not moving enough
j not moving enough
j not moving enough
迭代次数：107
j not moving enough
j not moving enough
j not moving enough
迭代次数：108
j not moving enough
j not moving enough
j not moving enough
迭代次数：109
j not moving enough
j not moving enough
j not moving enough
迭代次数：110
j not moving enough
j not moving enough
j not moving enough
迭代次数：111
j not moving enough
j not moving enough
j not moving enough
迭代次数：112
j not moving enough
j not moving enough
j not moving enough
迭代次数：113
j not moving enough
j not moving enough
j not moving enough
迭代次数：114
j not moving enough
j not moving enough
j not moving enough
迭代次数：115
j not moving enough
j not moving enough
j not moving enough
迭代次数：116
j not moving enough
j not moving enough
j not moving enough
迭代次数：117
j not moving enough
j not moving enough
j not moving enough
迭代次数：118
j not moving enough
j not moving enough
j not moving enough
迭代次数：119
j not moving enough
j not moving enough
j not moving enough
迭代次数：120
j not moving enough
j not moving enough
j not moving enough
迭代次数：121
j not moving enough
j not moving enough
j not moving enough
迭代次数：122
j not moving enough
j not moving enough
j not moving enough
迭代次数：123
j not moving enough
j not moving enough
j not moving enough
迭代次数：124
j not moving enough
j not moving enough
j not moving enough
迭代次数：125
j not moving enough
j not moving enough
j not moving enough
迭代次数：126
j not moving enough
j not moving enough
j not moving enough
迭代次数：127
j not moving enough
j not moving enough
j not moving enough
迭代次数：128
j not moving enough
j not moving enough
j not moving enough
迭代次数：129
j not moving enough
j not moving enough
j not moving enough
迭代次数：130
j not moving enough
j not moving enough
j not moving enough
迭代次数：131
j not moving enough
j not moving enough
j not moving enough
迭代次数：132
j not moving enough
j not moving enough
j not moving enough
迭代次数：133
j not moving enough
j not moving enough
j not moving enough
迭代次数：134
j not moving enough
j not moving enough
j not moving enough
迭代次数：135
j not moving enough
j not moving enough
j not moving enough
迭代次数：136
j not moving enough
j not moving enough
j not moving enough
迭代次数：137
j not moving enough
j not moving enough
j not moving enough
迭代次数：138
j not moving enough
j not moving enough
j not moving enough
迭代次数：139
j not moving enough
j not moving enough
j not moving enough
迭代次数：140
j not moving enough
j not moving enough
j not moving enough
迭代次数：141
j not moving enough
j not moving enough
j not moving enough
迭代次数：142
j not moving enough
j not moving enough
j not moving enough
迭代次数：143
j not moving enough
j not moving enough
j not moving enough
迭代次数：144
j not moving enough
j not moving enough
j not moving enough
迭代次数：145
j not moving enough
j not moving enough
j not moving enough
迭代次数：146
j not moving enough
j not moving enough
j not moving enough
迭代次数：147
j not moving enough
j not moving enough
j not moving enough
迭代次数：148
j not moving enough
j not moving enough
j not moving enough
迭代次数：149
j not moving enough
j not moving enough
j not moving enough
迭代次数：150
j not moving enough
j not moving enough
j not moving enough
迭代次数：151
j not moving enough
j not moving enough
j not moving enough
迭代次数：152
j not moving enough
j not moving enough
j not moving enough
迭代次数：153
j not moving enough
j not moving enough
j not moving enough
迭代次数：154
j not moving enough
j not moving enough
j not moving enough
迭代次数：155
j not moving enough
j not moving enough
j not moving enough
迭代次数：156
j not moving enough
j not moving enough
j not moving enough
迭代次数：157
j not moving enough
j not moving enough
j not moving enough
迭代次数：158
j not moving enough
j not moving enough
j not moving enough
迭代次数：159
j not moving enough
j not moving enough
j not moving enough
迭代次数：160
j not moving enough
j not moving enough
j not moving enough
迭代次数：161
j not moving enough
j not moving enough
j not moving enough
迭代次数：162
j not moving enough
j not moving enough
j not moving enough
迭代次数：163
j not moving enough
j not moving enough
j not moving enough
迭代次数：164
j not moving enough
j not moving enough
j not moving enough
迭代次数：165
j not moving enough
j not moving enough
j not moving enough
迭代次数：166
j not moving enough
j not moving enough
j not moving enough
迭代次数：167
j not moving enough
j not moving enough
j not moving enough
迭代次数：168
j not moving enough
j not moving enough
j not moving enough
迭代次数：169
j not moving enough
j not moving enough
j not moving enough
迭代次数：170
j not moving enough
j not moving enough
j not moving enough
迭代次数：171
j not moving enough
j not moving enough
j not moving enough
迭代次数：172
j not moving enough
j not moving enough
j not moving enough
迭代次数：173
j not moving enough
j not moving enough
j not moving enough
迭代次数：174
j not moving enough
j not moving enough
j not moving enough
迭代次数：175
j not moving enough
j not moving enough
j not moving enough
迭代次数：176
j not moving enough
j not moving enough
j not moving enough
迭代次数：177
j not moving enough
j not moving enough
j not moving enough
迭代次数：178
j not moving enough
j not moving enough
j not moving enough
迭代次数：179
j not moving enough
j not moving enough
j not moving enough
迭代次数：180
j not moving enough
j not moving enough
j not moving enough
迭代次数：181
j not moving enough
j not moving enough
j not moving enough
迭代次数：182
j not moving enough
j not moving enough
j not moving enough
迭代次数：183
j not moving enough
j not moving enough
j not moving enough
迭代次数：184
j not moving enough
j not moving enough
j not moving enough
迭代次数：185
j not moving enough
j not moving enough
j not moving enough
迭代次数：186
j not moving enough
j not moving enough
j not moving enough
迭代次数：187
j not moving enough
j not moving enough
j not moving enough
迭代次数：188
j not moving enough
j not moving enough
j not moving enough
迭代次数：189
j not moving enough
j not moving enough
j not moving enough
迭代次数：190
j not moving enough
j not moving enough
j not moving enough
迭代次数：191
j not moving enough
j not moving enough
j not moving enough
迭代次数：192
j not moving enough
j not moving enough
j not moving enough
迭代次数：193
j not moving enough
j not moving enough
j not moving enough
迭代次数：194
j not moving enough
j not moving enough
j not moving enough
迭代次数：195
j not moving enough
j not moving enough
j not moving enough
迭代次数：196
j not moving enough
j not moving enough
j not moving enough
迭代次数：197
j not moving enough
j not moving enough
j not moving enough
迭代次数：198
j not moving enough
j not moving enough
j not moving enough
迭代次数：199
j not moving enough
j not moving enough
j not moving enough
迭代次数：200
j not moving enough
j not moving enough
j not moving enough
迭代次数：201
j not moving enough
j not moving enough
j not moving enough
迭代次数：202
j not moving enough
j not moving enough
j not moving enough
迭代次数：203
j not moving enough
j not moving enough
j not moving enough
迭代次数：204
j not moving enough
j not moving enough
j not moving enough
迭代次数：205
j not moving enough
j not moving enough
j not moving enough
迭代次数：206
j not moving enough
j not moving enough
j not moving enough
迭代次数：207
j not moving enough
j not moving enough
j not moving enough
迭代次数：208
j not moving enough
j not moving enough
j not moving enough
迭代次数：209
j not moving enough
j not moving enough
j not moving enough
迭代次数：210
j not moving enough
j not moving enough
j not moving enough
迭代次数：211
j not moving enough
j not moving enough
j not moving enough
迭代次数：212
j not moving enough
j not moving enough
j not moving enough
迭代次数：213
j not moving enough
j not moving enough
j not moving enough
迭代次数：214
j not moving enough
j not moving enough
j not moving enough
迭代次数：215
j not moving enough
j not moving enough
j not moving enough
迭代次数：216
j not moving enough
j not moving enough
j not moving enough
迭代次数：217
j not moving enough
j not moving enough
j not moving enough
迭代次数：218
j not moving enough
j not moving enough
j not moving enough
迭代次数：219
j not moving enough
j not moving enough
j not moving enough
迭代次数：220
j not moving enough
j not moving enough
j not moving enough
迭代次数：221
j not moving enough
j not moving enough
j not moving enough
迭代次数：222
j not moving enough
j not moving enough
j not moving enough
迭代次数：223
j not moving enough
j not moving enough
j not moving enough
迭代次数：224
j not moving enough
j not moving enough
j not moving enough
迭代次数：225
j not moving enough
j not moving enough
j not moving enough
迭代次数：226
j not moving enough
j not moving enough
j not moving enough
迭代次数：227
j not moving enough
j not moving enough
j not moving enough
迭代次数：228
j not moving enough
j not moving enough
j not moving enough
迭代次数：229
j not moving enough
j not moving enough
j not moving enough
迭代次数：230
j not moving enough
j not moving enough
j not moving enough
迭代次数：231
j not moving enough
j not moving enough
j not moving enough
迭代次数：232
j not moving enough
j not moving enough
j not moving enough
迭代次数：233
j not moving enough
j not moving enough
j not moving enough
迭代次数：234
j not moving enough
j not moving enough
j not moving enough
迭代次数：235
j not moving enough
j not moving enough
j not moving enough
迭代次数：236
j not moving enough
j not moving enough
j not moving enough
迭代次数：237
j not moving enough
j not moving enough
j not moving enough
迭代次数：238
j not moving enough
j not moving enough
j not moving enough
迭代次数：239
j not moving enough
j not moving enough
j not moving enough
迭代次数：240
j not moving enough
j not moving enough
j not moving enough
迭代次数：241
j not moving enough
j not moving enough
j not moving enough
迭代次数：242
j not moving enough
j not moving enough
j not moving enough
迭代次数：243
j not moving enough
j not moving enough
j not moving enough
迭代次数：244
j not moving enough
j not moving enough
j not moving enough
迭代次数：245
j not moving enough
j not moving enough
j not moving enough
迭代次数：246
j not moving enough
j not moving enough
j not moving enough
迭代次数：247
j not moving enough
j not moving enough
j not moving enough
迭代次数：248
j not moving enough
j not moving enough
j not moving enough
迭代次数：249
j not moving enough
j not moving enough
j not moving enough
迭代次数：250
j not moving enough
j not moving enough
j not moving enough
迭代次数：251
j not moving enough
j not moving enough
j not moving enough
迭代次数：252
j not moving enough
j not moving enough
j not moving enough
迭代次数：253
j not moving enough
j not moving enough
j not moving enough
迭代次数：254
j not moving enough
j not moving enough
j not moving enough
迭代次数：255
j not moving enough
j not moving enough
j not moving enough
迭代次数：256
j not moving enough
j not moving enough
j not moving enough
迭代次数：257
j not moving enough
j not moving enough
j not moving enough
迭代次数：258
j not moving enough
j not moving enough
j not moving enough
迭代次数：259
j not moving enough
j not moving enough
j not moving enough
迭代次数：260
j not moving enough
j not moving enough
j not moving enough
迭代次数：261
j not moving enough
j not moving enough
j not moving enough
迭代次数：262
j not moving enough
j not moving enough
j not moving enough
迭代次数：263
j not moving enough
j not moving enough
j not moving enough
迭代次数：264
j not moving enough
j not moving enough
j not moving enough
迭代次数：265
j not moving enough
j not moving enough
j not moving enough
迭代次数：266
j not moving enough
j not moving enough
j not moving enough
迭代次数：267
j not moving enough
j not moving enough
j not moving enough
迭代次数：268
j not moving enough
j not moving enough
j not moving enough
迭代次数：269
j not moving enough
j not moving enough
j not moving enough
迭代次数：270
j not moving enough
j not moving enough
j not moving enough
迭代次数：271
j not moving enough
j not moving enough
j not moving enough
迭代次数：272
j not moving enough
j not moving enough
j not moving enough
迭代次数：273
j not moving enough
j not moving enough
j not moving enough
迭代次数：274
j not moving enough
j not moving enough
j not moving enough
迭代次数：275
j not moving enough
j not moving enough
j not moving enough
迭代次数：276
j not moving enough
j not moving enough
j not moving enough
迭代次数：277
j not moving enough
j not moving enough
j not moving enough
迭代次数：278
j not moving enough
j not moving enough
j not moving enough
迭代次数：279
j not moving enough
j not moving enough
j not moving enough
迭代次数：280
j not moving enough
j not moving enough
j not moving enough
迭代次数：281
j not moving enough
j not moving enough
j not moving enough
迭代次数：282
j not moving enough
j not moving enough
j not moving enough
迭代次数：283
j not moving enough
j not moving enough
j not moving enough
迭代次数：284
j not moving enough
j not moving enough
j not moving enough
迭代次数：285
j not moving enough
j not moving enough
j not moving enough
迭代次数：286
j not moving enough
j not moving enough
j not moving enough
迭代次数：287
j not moving enough
j not moving enough
j not moving enough
迭代次数：288
j not moving enough
j not moving enough
j not moving enough
迭代次数：289
j not moving enough
j not moving enough
j not moving enough
迭代次数：290
j not moving enough
j not moving enough
j not moving enough
迭代次数：291
j not moving enough
j not moving enough
j not moving enough
迭代次数：292
j not moving enough
j not moving enough
j not moving enough
迭代次数：293
j not moving enough
j not moving enough
j not moving enough
迭代次数：294
j not moving enough
j not moving enough
j not moving enough
迭代次数：295
j not moving enough
j not moving enough
j not moving enough
迭代次数：296
j not moving enough
j not moving enough
j not moving enough
迭代次数：297
j not moving enough
j not moving enough
j not moving enough
迭代次数：298
j not moving enough
j not moving enough
j not moving enough
迭代次数：299
j not moving enough
j not moving enough
j not moving enough
迭代次数：300
j not moving enough
j not moving enough
j not moving enough
迭代次数：301
j not moving enough
j not moving enough
j not moving enough
迭代次数：302
j not moving enough
j not moving enough
j not moving enough
迭代次数：303
j not moving enough
j not moving enough
j not moving enough
迭代次数：304
j not moving enough
j not moving enough
j not moving enough
迭代次数：305
j not moving enough
j not moving enough
j not moving enough
迭代次数：306
j not moving enough
j not moving enough
j not moving enough
迭代次数：307
j not moving enough
j not moving enough
j not moving enough
迭代次数：308
j not moving enough
j not moving enough
j not moving enough
迭代次数：309
j not moving enough
j not moving enough
j not moving enough
迭代次数：310
j not moving enough
j not moving enough
j not moving enough
迭代次数：311
j not moving enough
j not moving enough
j not moving enough
迭代次数：312
j not moving enough
j not moving enough
j not moving enough
迭代次数：313
j not moving enough
j not moving enough
j not moving enough
迭代次数：314
j not moving enough
j not moving enough
j not moving enough
迭代次数：315
j not moving enough
j not moving enough
j not moving enough
迭代次数：316
j not moving enough
j not moving enough
j not moving enough
迭代次数：317
j not moving enough
j not moving enough
j not moving enough
迭代次数：318
j not moving enough
j not moving enough
j not moving enough
迭代次数：319
j not moving enough
j not moving enough
j not moving enough
迭代次数：320
j not moving enough
j not moving enough
j not moving enough
迭代次数：321
j not moving enough
j not moving enough
j not moving enough
迭代次数：322
j not moving enough
j not moving enough
j not moving enough
迭代次数：323
j not moving enough
j not moving enough
j not moving enough
迭代次数：324
j not moving enough
j not moving enough
j not moving enough
迭代次数：325
j not moving enough
j not moving enough
j not moving enough
迭代次数：326
j not moving enough
j not moving enough
j not moving enough
迭代次数：327
j not moving enough
j not moving enough
j not moving enough
迭代次数：328
j not moving enough
j not moving enough
j not moving enough
迭代次数：329
j not moving enough
j not moving enough
j not moving enough
迭代次数：330
j not moving enough
j not moving enough
j not moving enough
迭代次数：331
j not moving enough
j not moving enough
j not moving enough
迭代次数：332
j not moving enough
j not moving enough
j not moving enough
迭代次数：333
j not moving enough
j not moving enough
j not moving enough
迭代次数：334
j not moving enough
j not moving enough
j not moving enough
迭代次数：335
j not moving enough
j not moving enough
j not moving enough
迭代次数：336
j not moving enough
j not moving enough
j not moving enough
迭代次数：337
j not moving enough
j not moving enough
j not moving enough
迭代次数：338
j not moving enough
j not moving enough
j not moving enough
迭代次数：339
j not moving enough
j not moving enough
j not moving enough
迭代次数：340
j not moving enough
j not moving enough
j not moving enough
迭代次数：341
j not moving enough
j not moving enough
j not moving enough
迭代次数：342
j not moving enough
j not moving enough
j not moving enough
迭代次数：343
j not moving enough
j not moving enough
j not moving enough
迭代次数：344
j not moving enough
j not moving enough
j not moving enough
迭代次数：345
j not moving enough
j not moving enough
j not moving enough
迭代次数：346
j not moving enough
j not moving enough
j not moving enough
迭代次数：347
j not moving enough
j not moving enough
j not moving enough
迭代次数：348
j not moving enough
j not moving enough
j not moving enough
迭代次数：349
j not moving enough
j not moving enough
j not moving enough
迭代次数：350
j not moving enough
j not moving enough
j not moving enough
迭代次数：351
j not moving enough
j not moving enough
j not moving enough
迭代次数：352
j not moving enough
j not moving enough
j not moving enough
迭代次数：353
j not moving enough
j not moving enough
j not moving enough
迭代次数：354
j not moving enough
j not moving enough
j not moving enough
迭代次数：355
j not moving enough
j not moving enough
j not moving enough
迭代次数：356
j not moving enough
j not moving enough
j not moving enough
迭代次数：357
j not moving enough
j not moving enough
j not moving enough
迭代次数：358
j not moving enough
j not moving enough
j not moving enough
迭代次数：359
j not moving enough
j not moving enough
j not moving enough
迭代次数：360
j not moving enough
j not moving enough
j not moving enough
迭代次数：361
j not moving enough
j not moving enough
j not moving enough
迭代次数：362
j not moving enough
j not moving enough
j not moving enough
迭代次数：363
j not moving enough
j not moving enough
j not moving enough
迭代次数：364
j not moving enough
j not moving enough
j not moving enough
迭代次数：365
j not moving enough
j not moving enough
j not moving enough
迭代次数：366
j not moving enough
j not moving enough
j not moving enough
迭代次数：367
j not moving enough
j not moving enough
j not moving enough
迭代次数：368
j not moving enough
j not moving enough
j not moving enough
迭代次数：369
j not moving enough
j not moving enough
j not moving enough
迭代次数：370
j not moving enough
j not moving enough
j not moving enough
迭代次数：371
j not moving enough
j not moving enough
j not moving enough
迭代次数：372
j not moving enough
j not moving enough
j not moving enough
迭代次数：373
j not moving enough
j not moving enough
j not moving enough
迭代次数：374
j not moving enough
j not moving enough
j not moving enough
迭代次数：375
j not moving enough
j not moving enough
j not moving enough
迭代次数：376
j not moving enough
j not moving enough
j not moving enough
迭代次数：377
j not moving enough
j not moving enough
j not moving enough
迭代次数：378
j not moving enough
j not moving enough
j not moving enough
迭代次数：379
j not moving enough
j not moving enough
j not moving enough
迭代次数：380
j not moving enough
j not moving enough
j not moving enough
迭代次数：381
j not moving enough
j not moving enough
j not moving enough
迭代次数：382
j not moving enough
j not moving enough
j not moving enough
迭代次数：383
j not moving enough
j not moving enough
j not moving enough
迭代次数：384
j not moving enough
j not moving enough
j not moving enough
迭代次数：385
j not moving enough
j not moving enough
j not moving enough
迭代次数：386
j not moving enough
j not moving enough
j not moving enough
迭代次数：387
j not moving enough
j not moving enough
j not moving enough
迭代次数：388
j not moving enough
j not moving enough
j not moving enough
迭代次数：389
j not moving enough
j not moving enough
j not moving enough
迭代次数：390
j not moving enough
j not moving enough
j not moving enough
迭代次数：391
j not moving enough
j not moving enough
j not moving enough
迭代次数：392
j not moving enough
j not moving enough
j not moving enough
迭代次数：393
j not moving enough
j not moving enough
j not moving enough
迭代次数：394
j not moving enough
j not moving enough
j not moving enough
迭代次数：395
j not moving enough
j not moving enough
j not moving enough
迭代次数：396
j not moving enough
j not moving enough
j not moving enough
迭代次数：397
j not moving enough
j not moving enough
j not moving enough
迭代次数：398
j not moving enough
j not moving enough
j not moving enough
迭代次数：399
j not moving enough
j not moving enough
j not moving enough
迭代次数：400
j not moving enough
j not moving enough
j not moving enough
迭代次数：401
j not moving enough
j not moving enough
j not moving enough
迭代次数：402
j not moving enough
j not moving enough
j not moving enough
迭代次数：403
j not moving enough
j not moving enough
j not moving enough
迭代次数：404
j not moving enough
j not moving enough
j not moving enough
迭代次数：405
j not moving enough
j not moving enough
j not moving enough
迭代次数：406
j not moving enough
j not moving enough
j not moving enough
迭代次数：407
j not moving enough
j not moving enough
j not moving enough
迭代次数：408
j not moving enough
j not moving enough
j not moving enough
迭代次数：409
j not moving enough
j not moving enough
j not moving enough
迭代次数：410
j not moving enough
j not moving enough
j not moving enough
迭代次数：411
j not moving enough
j not moving enough
j not moving enough
迭代次数：412
j not moving enough
j not moving enough
j not moving enough
迭代次数：413
j not moving enough
j not moving enough
j not moving enough
迭代次数：414
j not moving enough
j not moving enough
j not moving enough
迭代次数：415
j not moving enough
j not moving enough
j not moving enough
迭代次数：416
j not moving enough
j not moving enough
j not moving enough
迭代次数：417
j not moving enough
j not moving enough
j not moving enough
迭代次数：418
j not moving enough
j not moving enough
j not moving enough
迭代次数：419
j not moving enough
j not moving enough
j not moving enough
迭代次数：420
j not moving enough
j not moving enough
j not moving enough
迭代次数：421
j not moving enough
j not moving enough
j not moving enough
迭代次数：422
j not moving enough
j not moving enough
j not moving enough
迭代次数：423
j not moving enough
j not moving enough
j not moving enough
迭代次数：424
j not moving enough
j not moving enough
j not moving enough
迭代次数：425
j not moving enough
j not moving enough
j not moving enough
迭代次数：426
j not moving enough
j not moving enough
j not moving enough
迭代次数：427
j not moving enough
j not moving enough
j not moving enough
迭代次数：428
j not moving enough
j not moving enough
j not moving enough
迭代次数：429
j not moving enough
j not moving enough
j not moving enough
迭代次数：430
j not moving enough
j not moving enough
j not moving enough
迭代次数：431
j not moving enough
j not moving enough
j not moving enough
迭代次数：432
j not moving enough
j not moving enough
j not moving enough
迭代次数：433
j not moving enough
j not moving enough
j not moving enough
迭代次数：434
j not moving enough
j not moving enough
j not moving enough
迭代次数：435
j not moving enough
j not moving enough
j not moving enough
迭代次数：436
j not moving enough
j not moving enough
j not moving enough
迭代次数：437
j not moving enough
j not moving enough
j not moving enough
迭代次数：438
j not moving enough
j not moving enough
j not moving enough
迭代次数：439
j not moving enough
j not moving enough
j not moving enough
迭代次数：440
j not moving enough
j not moving enough
j not moving enough
迭代次数：441
j not moving enough
j not moving enough
j not moving enough
迭代次数：442
j not moving enough
j not moving enough
j not moving enough
迭代次数：443
j not moving enough
j not moving enough
j not moving enough
迭代次数：444
j not moving enough
j not moving enough
j not moving enough
迭代次数：445
j not moving enough
j not moving enough
j not moving enough
迭代次数：446
j not moving enough
j not moving enough
j not moving enough
迭代次数：447
j not moving enough
j not moving enough
j not moving enough
迭代次数：448
j not moving enough
j not moving enough
j not moving enough
迭代次数：449
j not moving enough
j not moving enough
j not moving enough
迭代次数：450
j not moving enough
j not moving enough
j not moving enough
迭代次数：451
j not moving enough
j not moving enough
j not moving enough
迭代次数：452
j not moving enough
j not moving enough
j not moving enough
迭代次数：453
j not moving enough
j not moving enough
j not moving enough
迭代次数：454
j not moving enough
j not moving enough
j not moving enough
迭代次数：455
j not moving enough
j not moving enough
j not moving enough
迭代次数：456
j not moving enough
j not moving enough
j not moving enough
迭代次数：457
j not moving enough
j not moving enough
j not moving enough
迭代次数：458
j not moving enough
j not moving enough
j not moving enough
迭代次数：459
j not moving enough
j not moving enough
j not moving enough
迭代次数：460
j not moving enough
j not moving enough
j not moving enough
迭代次数：461
j not moving enough
j not moving enough
j not moving enough
迭代次数：462
j not moving enough
j not moving enough
j not moving enough
迭代次数：463
j not moving enough
j not moving enough
j not moving enough
迭代次数：464
j not moving enough
j not moving enough
j not moving enough
迭代次数：465
j not moving enough
j not moving enough
j not moving enough
迭代次数：466
j not moving enough
j not moving enough
j not moving enough
迭代次数：467
j not moving enough
j not moving enough
j not moving enough
迭代次数：468
j not moving enough
j not moving enough
j not moving enough
迭代次数：469
j not moving enough
j not moving enough
j not moving enough
迭代次数：470
j not moving enough
j not moving enough
j not moving enough
迭代次数：471
j not moving enough
j not moving enough
j not moving enough
迭代次数：472
j not moving enough
j not moving enough
j not moving enough
迭代次数：473
j not moving enough
j not moving enough
j not moving enough
迭代次数：474
j not moving enough
j not moving enough
j not moving enough
迭代次数：475
j not moving enough
j not moving enough
j not moving enough
迭代次数：476
j not moving enough
j not moving enough
j not moving enough
迭代次数：477
j not moving enough
j not moving enough
j not moving enough
迭代次数：478
j not moving enough
j not moving enough
j not moving enough
迭代次数：479
j not moving enough
j not moving enough
j not moving enough
迭代次数：480
j not moving enough
j not moving enough
j not moving enough
迭代次数：481
j not moving enough
j not moving enough
j not moving enough
迭代次数：482
j not moving enough
j not moving enough
j not moving enough
迭代次数：483
j not moving enough
j not moving enough
j not moving enough
迭代次数：484
j not moving enough
j not moving enough
j not moving enough
迭代次数：485
j not moving enough
j not moving enough
j not moving enough
迭代次数：486
j not moving enough
j not moving enough
j not moving enough
迭代次数：487
j not moving enough
j not moving enough
j not moving enough
迭代次数：488
j not moving enough
j not moving enough
j not moving enough
迭代次数：489
j not moving enough
j not moving enough
j not moving enough
迭代次数：490
j not moving enough
j not moving enough
j not moving enough
迭代次数：491
j not moving enough
j not moving enough
j not moving enough
迭代次数：492
j not moving enough
j not moving enough
j not moving enough
迭代次数：493
j not moving enough
j not moving enough
j not moving enough
迭代次数：494
j not moving enough
j not moving enough
j not moving enough
迭代次数：495
j not moving enough
j not moving enough
j not moving enough
迭代次数：496
j not moving enough
j not moving enough
j not moving enough
迭代次数：497
j not moving enough
j not moving enough
j not moving enough
迭代次数：498
j not moving enough
j not moving enough
j not moving enough
迭代次数：499
j not moving enough
j not moving enough
j not moving enough
迭代次数：500

b

matrix([[-3.83785102]])

alphas[alphas>0]

matrix([[0.1273855 , 0.24131542, 0.36872064]])

np.shape(alphas[alphas>0])

(1, 3)

for i in range(100):
    if alphas[i] > 0.0:
        print(dataArr[i],labelArr[i])

[4.658191, 3.507396] -1.0
[3.457096, -0.082216] -1.0
[6.080573, 0.418886] 1.0

#分类结果可视化
def showClassifer(dataMat, w, b):
    #绘制样本点
    data_plus = []                                  #正样本
    data_minus = []                                 #负样本
    for i in range(len(dataMat)):
        if labelMat[i] > 0:
            data_plus.append(dataMat[i])
        else:
            data_minus.append(dataMat[i])
    data_plus_np = np.array(data_plus)              #转换为numpy矩阵
    data_minus_np = np.array(data_minus)            #转换为numpy矩阵
    plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1], s=30, alpha=0.7)   #正样本散点图
    plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1], s=30, alpha=0.7) #负样本散点图
    #绘制直线
    x1 = max(dataMat)[0]
    x2 = min(dataMat)[0]
    a1, a2 = w
    b = float(b)
    a1 = float(a1[0])
    a2 = float(a2[0])
    y1, y2 = (-b- a1*x1)/a2, (-b - a1*x2)/a2
    plt.plot([x1, x2], [y1, y2])
    #找出支持向量点
    for i, alpha in enumerate(alphas):
        if abs(alpha) > 0:
            x, y = dataMat[i]
            plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')
    plt.show()

#计算w
def get_w(dataMat, labelMat, alphas):
    alphas, dataMat, labelMat = np.array(alphas), np.array(dataMat), np.array(labelMat)
    w = np.dot((np.tile(labelMat.reshape(1, -1).T, (1, 2)) * dataMat).T, alphas)
    return w.tolist()

w = get_w(dataMat,labelMat,alphas)

showClassifer(dataMat,w,b)

png

机器学习 - 使用 Python 实现支持向量机
学习使你进步。
09-19 841
支持向量机（Support Vector Machines，简称 SVM）是一种强大的机器学习算法，被广泛应用于分类和回归问题。对于非线性可分的数据集，我们可以使用其他核函数，如高斯核函数（Gaussian kernel）。通过调整不同的核函数和参数，我们可以适应不同类型的数据集并获得良好的分类或回归性能。假设我们有一个二维的训练数据集，其中包含两个类别的样本点。训练完成后，我们可以使用模型对新的数据点进行回归预测。训练完成后，我们可以使用训练好的模型对新的数据点进行分类预测。将输出预测的类别标签。
python支持向量机
11-22
支持向量机python代码，也用于二分类，对新手学习了解支持向量机很有帮助
支持向量机以及python实现
weixin_59049646的博客
06-11 3755
它通过寻找最优的决策边界，即最大间隔超平面，来对数据进行分类。
python回归算法_支持向量回归（SVR）
最新发布
2301_81791289的博客
02-10 1353
支持向量回归（SVR）
支持向量机Python实现
ruosiliu_123的博客
07-17 817
SVM中C参数（松弛向量的系数）和gamma参数（RBF函数中的参数）的改变对分类效果的影响如下：from sklearn import datasets import numpy as np from sklearn.cross_validation import train_test_split import matplotlib.pyplot as plt from matplotlib.co
支持向量机源码Python实现
06-12
SVM支持向量机Python实现，大家可以当备用资料存储，也可以直接实际操作
机器学习实战(第六章-支持向量机-所有代码与详细注解-python3.7)
12-18
本章聚焦于通过Python 3.7实现支持向量机，提供详尽的代码注解，帮助读者深入理解其工作原理。 一、支持向量机基本概念 支持向量机的核心思想是找到一个最优超平面，该超平面能够最大程度地将不同类别的数据分开。...
近似线性可分支持向量机Python代码实现
10-27
采用软间隔最大化策略，代码解释说明的博客地址：https://blog.csdn.net/u013172930/article/details/143270417
支持向量机python实现
Cherry的博客
03-19 474
有问题欢迎和我联系，加微信下图 import numpy as np import pandas as pd from sklearn.svm import SVR from sklearn.metrics import mean_absolute_error, mean_squared_error import matplotlib.pyplot as plt import datetime start = datetime.datetime.now() df = pd.read_csv("./dat
SVM.py,支持向量机的python 代码实现
06-17
SVM.py,支持向量机的python 代码实现
Python 支持向量机
weixin_45659364的博客
04-29 4977
学习目标： Python代码实现向量机 学习内容： 支持向量机，是属于统计学习中的一种常见算法，但这种算法如果使用计算器计算的话也是浪费时间，哪怕是用计算机计算，也会很麻烦，所以使用代码来进行计算，简单快捷。 要实现的功能也很简单，我们传入一个文件，文件中写有相关数据，然后代码自动计算w和b在，以及其它的一些参数，如下图，是我们的实现结果 代码实现： 直接上代码吧 from numpy import * import matplotlib.pyplot as plt from sklearn impo
支持向量机 及其分类案例详解（附Python 代码）
qq_39538718的博客
07-27 1490
我们将构建一个支持向量机（SVM）分类器，以预测一个人基于14个属性的收入等级。我们的目标是判断收入是否高于或低于每年$50,000。因此，这是一个二元分类问题。我们将使用在可用的人口普查收入数据集。需要注意的是，此数据集中的每个数据点都是单词和数字的混合。我们不能使用原始格式的数据，因为算法不知道如何处理单词。我们不能使用标签编码器转换所有数据，因为数值数据是有价值的。因此，我们需要结合使用标签编码器和原始数值数据来构建一个有效的分类器。
Python机器学习：支持向量机
faltas的博客
04-12 880
支持向量机
支持向量机python代码_支持向量机及python实现（一）
weixin_39609527的博客
11-23 510
支持向量机英文名称Support Vector Machine简称SVM，它是由前苏联科学家Corinna Cortes在1995年首先提出的，它在解决小样本、非线性及高维模式识别中表现出许多特有的优势，并能够推广应用到函数拟合等其他机器学习问题中.SVM是一种二分类模型，它的目的是寻找一个超平面来对样本进行分割，分割的原则是间隔最大化，最终转化为一个凸二次规划问题来求解. 在机器学习中，使用支持...
Python学习入门之支持向量机
qq_74868273的博客
08-01 2338
支持向量机（Support Vector Machine，SVM）是一种强大的监督学习模型，广泛应用于分类和回归分析。其核心思想是将数据点映射到高维空间，以便找到一个最佳的超平面将不同类别的数据有效分开。本文将介绍支持向量机的基本概念、原理以及如何使用 Python 实现 SVM。支持向量机是一种强大的分类算法，其通过构建最大间隔决策边界，能够有效处理线性和非线性问题。利用 Python 和库，我们可以轻松实现支持向量机模型。随着实际应用的深入，我们可以探索更复杂的模型和参数调整，以优化性能。
机器学习作业班_python实现支持向量机
lzay的博客
02-27 336
支持向量机 在本练习中，我们将使用支持向量机（SVM）来构建垃圾邮件分类器。 我们将从一些简单的2D数据集开始使用SVM来查看它们的工作原理。 然后，我们将对一组原始电子邮件进行一些预处理工作，并使用SVM在处理的电子邮件上构建分类器，以确定它们是否为垃圾邮件。 我们要做的第一件事是看一个简单的二维数据集，看看线性SVM如何对数据集进行不同的C值（类似于线性/逻辑回归中的正则化项）。 import...
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

顾道长生'

您的支持是我创作的动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值