
7.1 线性可分支持向量机与硬间隔最大化
7.1.1 线性可分支持向量机
当训练数据集线性可分时,存在无穷个分离超平面可将两类数据正确分开。
- 感知机利用误分类最小的策略,求得分离超平面,不过这时的解有无穷多个。
- 线性可分支持向量机利用间隔最大化求最优分离超平面,这时,解是唯一的。
线性可分支持向量机 给定线性可分训练数据集,通过间隔最大化或
等价地求解相应的凸二次规划问题学习得到的分离超平面为
w ∗ ⋅ x + b ∗ = 0 w^{*} \cdot x+b^{*}=0 w∗⋅x+b∗=0
以及相应的分类决策函数
f ( x ) = sign ( w ∗ ⋅ x + b ∗ ) f(x)=\operatorname{sign}\left(w^{*} \cdot x+b^{*}\right) f(x)=sign(w∗⋅x+b∗)
称为线性可分支持向量机。
通俗解释,距离超平面最近的实例,距离最大,所以是唯一的平面。
7.1.2 函数间隔和几何间隔
一个点距离分离超平面的远近可以表示分类预测的确信程度。
-
函数间隔 对于给定的训练数据集 T T T 和超平面 ( w , b ) (w, b) (w,b), 定义超平面 ( w , b ) (w, b) (w,b) 关于样本点 ( x i , y i ) \left(x_{i}, y_{i}\right) (xi,yi) 的函数间隔为
γ ^ i = y i ( w ⋅ x i + b ) \hat{\gamma}_{i}=y_{i}\left(w \cdot x_{i}+b\right) γ^i=yi(w⋅xi+b)定义超平面 ( w , b ) (w, b) (w,b) 关于训练数据集 T T T 的函数间隔为超平面 ( w , b ) (w, b) (w,b) 关于 T T T 中所有 样本点 ( x i , y i ) \left(x_{i}, y_{i}\right) (xi,yi) 的函数间隔之最小值, 即
γ ^ = min i = 1 , ⋯ , N γ ^ i \hat{\gamma}=\min _{i=1, \cdots, N} \hat{\gamma}_{i} γ^=i=1,⋯,Nminγ^i函数间隔可以表示分类预测的正确性及确信度。
-
几何间隔 对于给定的训练数据集 T T T 和超平面 ( w , b ) (w, b) (w,b), 定义超平面 ( w , b ) (w, b) (w,b) 关于样本点 ( x i , y i ) \left(x_{i}, y_{i}\right) (xi,yi) 的几何间隔为
γ i = y i ( w ∥ w ∥ ⋅ x i + b ∥ w ∥ ) \gamma_{i}=y_{i}\left(\frac{w}{\|w\|} \cdot x_{i}+\frac{b}{\|w\|}\right) γi=yi(∥w∥w⋅xi+∥w∥b)其中, ∥ w ∥ \|w\| ∥w∥是 w w w的 L 2 L2 L2范数。
定义超平面 ( w , b ) (w, b) (w,b) 关于训练数据集 T T T 的几何间隔为超平面 ( w , b ) (w, b) (w,b) 关于 T T T 中所有 样本点 ( x i , y i ) \left(x_{i}, y_{i}\right) (xi,yi) 的几何间隔之最小值, 即
γ = min i = 1 , ⋯ , N γ i \gamma=\min _{i=1, \cdots, N} \gamma_{i} γ=i=1,⋯,Nminγi -
超平面 ( w , b ) (w, b) (w,b) 关于样本点 ( x i , y i ) \left(x_{i}, y_{i}\right) (xi,yi) 的几何间隔一般是实例点到超平面的带符号的距离(signed distance), 当样本点被超平面正确分类时就是实例点到超平面的距离。
函数间隔和几何间隔有 下面的关系:
γ i = γ ^ i ∥ w ∥ γ = γ ^ ∥ w ∥ \begin{aligned} &\gamma_{i}=\frac{\hat{\gamma}_{i}}{\|w\|} \\ &\gamma=\frac{\hat{\gamma}}{\|w\|} \end{aligned} γi=∥w∥γ^iγ=∥w∥γ^ -
L 2 L2 L2范数:向量元素绝对值的平方和再开平方, ∥ x ∥ 2 = ∑ i = 1 N x i 2 \|x\|_{2}=\sqrt{\sum_{i=1}^{N} x_{i}^{2}} ∥x∥2=∑i=1Nxi2
7.1.3 间隔最大化
知识补充-凸优化
凸优化问题
- 目标函数是凸函数
- 可行域是凸集
- 局部最优解=全局最优解
凸集的定义: 对于一个点的集合 C \mathrm{C} C, 有 x , y \mathrm{x}, \mathrm{y} x,y 它都是属于 C 里面的两个点, 它们两点的连线中任何一点也是属于集合 C \mathrm{C} C的,
θ x + ( 1 − θ ) y ∈ C \theta x+(1-\theta) y \in C θx+(1−θ)y∈C
0 ≤ θ ≤ 1 0\le \theta \le 1 0≤θ≤1
典型的凸集
欧式空间 R n R^{n} Rn
x , y ∈ R n ⇒ θ x + ( 1 − θ ) y ∈ R n x, y \in R^{n} \Rightarrow \theta x+(1-\theta) y \in R^{n} x,y∈Rn⇒θx+(1−θ)y∈Rn
它的意义在于,很多时候可行域就是欧式空间, 那肯定是凸集凸集的交集还是凸集
仿射函数 f ( x ) f(x) f(x) 称为仿射函数, 如果它满足 f ( x ) = a ⋅ x + b , a ∈ R n , b ∈ R , x ∈ R n f(x)=a \cdot x+b, a \in \mathbf{R}^{n}, b \in \mathbf{R}, x \in \mathbf{R}^{n} f(x)=a⋅x+b,a∈Rn,b∈R,x∈Rn 。
支持向量机学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。(这里的间隔最大化又称为硬间隔最大化)
-
最大间隔分离超平面
max w , b γ s.t. y i ( w ∥ w ∥ ⋅ x i + b ∥ w ∥ ) ⩾ γ , i = 1 , 2 , ⋯ , N \begin{array}{ll} \max _{w, b} & \gamma \\ \text { s.t. } & y_{i}\left(\frac{w}{\|w\|} \cdot x_{i}+\frac{b}{\|w\|}\right) \geqslant \gamma, \quad i=1,2, \cdots, N \end{array} maxw,b s.t. γyi(∥w∥w⋅xi+∥w∥b)⩾γ,i=1,2,⋯,N最大化超平面 ( w , b ) (w, b) (w,b) 关于训练数据集的几何间隔 γ \gamma γ, 约束条件表示的是超平面 ( w , b ) (w, b) (w,b) 关于每个训练样本点的几何间隔至少是 γ 。 \gamma_{\text {。 }} γ。
考虑几何间隔和函数间隔的关系式 γ = γ ^ ∥ w ∥ \gamma=\frac{\hat{\gamma}}{\|w\|} γ=∥w∥γ^, 可将这个问题改写为
max w , b γ ^ ∥ w ∥ s.t. y i ( w ⋅ x i + b ) ⩾ γ ^ , i = 1 , 2 , ⋯ , N \begin{array}{ll} \max _{w, b} & \frac{\hat{\gamma}}{\|w\|} \\ \text { s.t. } & y_{i}\left(w \cdot x_{i}+b\right) \geqslant \hat{\gamma}, \quad i=1,2, \cdots, N \end{array} maxw,b s.t. ∥w∥γ^yi(w⋅xi+b)⩾γ^,i=1,2,⋯,N函数间隔 γ ^ \hat{\gamma} γ^ 的取值并不影响最优化问题的解。事实上, 假设将 w w w 和 b b b 按比例改 变为 λ w \lambda w λw 和 λ b \lambda b λb, 这时函数间隔成为 λ γ ^ ∘ \lambda \hat{\gamma}_{\circ} λγ^∘ 函数间隔的这一改变对上面最优化问题的不等式约束没有影响, 对目标函数的优化也没有影响, 也就是说, 它产生一个等价的最
优化问题。这样, 就可以取 γ ^ = 1 \hat{\gamma}=1 γ^=1 。 将 γ ^ = 1 \hat{\gamma}=1 γ^=1 代入上面的最优化问题, 注意到最大化 1 ∥ w ∥ \frac{1}{\|w\|} ∥w∥1 和最小化 1 2 ∥ w ∥ 2 \frac{1}{2}\|w\|^{2} 21∥w∥2 是等价的, 于是就得到下面的线性可分支持向量机学习的最优化问题:
min w , b 1 2 ∥ w ∥ 2 s.t. y i ( w ⋅ x i + b ) − 1 ⩾ 0 , i = 1 , 2 , ⋯ , N \begin{array}{ll} \min _{w, b} & \frac{1}{2}\|w\|^{2} \\ \text { s.t. } & y_{i}\left(w \cdot x_{i}+b\right)-1 \geqslant 0, \quad i=1,2, \cdots, N \end{array} minw,b s.t. 21∥w∥2yi(w⋅xi+b)−1⩾0,i=1,2,⋯,N这是一个凸二次规划 (convex quadratic programming) 问题。
凸优化问题是指约束最优化问题
min w f ( w ) s.t. g i ( w ) ⩽ 0 , i = 1 , 2 , ⋯ , k h i ( w ) = 0 , i = 1 , 2 , ⋯ , l \begin{array}{ll} \min _{w} & f(w) \\ \text { s.t. } & g_{i}(w) \leqslant 0, \quad i=1,2, \cdots, k \\ & h_{i}(w)=0, \quad i=1,2, \cdots, l \end{array} minw s.t. f(w)gi(w)⩽0,i=1,2,⋯,khi(w)=0,i=1,2,⋯,l
其中, 目标函数 f ( w ) f(w) f(w) 和约束函数 g i ( w ) g_{i}(w) gi(w) 都是 R n \mathbf{R}^{n} Rn 上的连续可微的品函数, 约束函数 h i ( w ) h_{i}(w) hi(w) 是 R n \mathbf{R}^{n} Rn 上的仿射函数。
最大间隔法
输入: 线性可分训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{N}, y_{N}\right)\right\} T={(x1,y1),(x2,y2),⋯,(xN,yN)}, 其中, x i ∈ x_{i} \in xi∈ X = R n , y i ∈ Y = { − 1 , + 1 } , i = 1 , 2 , ⋯ , N \mathcal{X}=\mathbf{R}^{n}, y_{i} \in \mathcal{Y}=\{-1,+1\}, i=1,2, \cdots, N X=Rn,yi∈Y={−1,+1},i=1,2,⋯,N
输出: 最大间隔分离超平面和分类决策函数。
(1)构造并求解约束最优化问题:
min w , b 1 2 ∥ w ∥ 2 s.t. y i ( w ⋅ x i + b ) − 1 ⩾ 0 , i = 1 , 2 , ⋯ , N \begin{array}{ll} \min _{w, b} & \frac{1}{2}\|w\|^{2} \\ \text { s.t. } & y_{i}\left(w \cdot x_{i}+b\right)-1 \geqslant 0, \quad i=1,2, \cdots, N \end{array} minw,b s.t. 21∥w∥2yi(w⋅xi+b)−1⩾0,i=1,2,⋯,N求得最优解 w ∗ , b ∗ w^{*}, b^{*} w∗,b∗ 。
(2)由此得到分离超平面:
w ∗ ⋅ x + b ∗ = 0 w^{*} \cdot x+b^{*}=0 w∗⋅x+b∗=0分类决策函数
f ( x ) = sign ( w ∗ ⋅ x + b ∗ ) f(x)=\operatorname{sign}\left(w^{*} \cdot x+b^{*}\right) f(x)=sign(w∗⋅x+b∗) -
最大间隔分离超平面的存在唯一性
最大间隔分离超平面的存在唯一性 若训练数据集T线性可分,则可将训练数据集中的样本点完全正确分开的最大间隔分离超平面存在且唯一。
证明:-
存在性
由于训练数据集线性可分,所以上述最优化问题一定存在可行解。又由于目标函数有下界,所以最优化问题必有解,记作 ( w ∗ , b ∗ ) (w^*,b^*) (w∗,b∗),由于训练数据集中既有正类点又有负类点,所以 ( w , b ) (w, b) (w,b) = (0,b)不是最优化的可行解,因而最优解 ( w ∗ , b ∗ ) (w^*,b^*) (w∗,b∗)必满足 w ∗ ≠ 0 w^*\ne 0 w∗=0,由此得知分离超平面的存在性。 -
唯一性
首先证明 w ∗ w^{*} w∗ 的唯一性。假设最优化问题存在两个最优解 ( w 1 ∗ , b 1 ∗ ) \left(w_{1}^{*}, b_{1}^{*}\right) (w1∗,b1∗) 和 ( w 2 ∗ , b 2 ∗ ) \left(w_{2}^{*}, b_{2}^{*}\right) (w2∗,b2∗) 。显然 ∥ w 1 ∗ ∥ = ∥ w 2 ∗ ∥ = c \left\|w_{1}^{*}\right\|=\left\|w_{2}^{*}\right\|=c ∥w1∗∥=∥w2∗∥=c, 其中 c c c 是一个常数。令 w = w 1 ∗ + w 2 ∗ 2 , b = b 1 ∗ + b 2 ∗ 2 w=\frac{w_{1}^{*}+w_{2}^{*}}{2}, b=\frac{b_{1}^{*}+b_{2}^{*}}{2} w=2w1∗+w2∗,b=2b1∗+b2∗, 易知 ( w , b ) (w, b) (w,b) 是最优化问题的可行解,从而有
c ⩽ ∥ w ∥ = ∣ 1 2 ∥ w 1 ∗ ∥ + 1 2 ∥ w 2 ∗ ∥ ∣ ⩽ 1 2 ∥ w 1 ∗ ∥ + 1 2 ∥ w 2 ∗ ∥ = c c \leqslant\|w\| =|\frac{1}{2}\left\|w_{1}^{*}\right\|+\frac{1}{2}\left\|w_{2}^{*}\right\||\leqslant \frac{1}{2}\left\|w_{1}^{*}\right\|+\frac{1}{2}\left\|w_{2}^{*}\right\|=c c⩽∥w∥=∣21∥w1∗∥+21∥w2∗∥∣⩽21∥w1∗∥+21∥w2∗∥=c上式表明, 式中的不等号必须为等号, 即 ∥ w ∥ = 1 2 ∥ w 1 ∗ ∥ + 1 2 ∥ w 2 ∗ ∥ \|w\|=\frac{1}{2}\left\|w_{1}^{*}\right\|+\frac{1}{2}\left\|w_{2}^{*}\right\| ∥w∥=21∥w1∗∥+21∥w2∗∥, 从而有 w 1 ∗ = w_{1}^{*}= w1∗= λ w 2 ∗ , ∣ λ ∣ = 1 \lambda w_{2}^{*},|\lambda|=1 λw2∗,∣λ∣=1 。 若 λ = − 1 \lambda=-1 λ=−1, 则 w = 0 , ( w , b ) w=0,(w, b) w=0,(w,b) 不是最优化问题的可行解, 矛盾。 因此必有 λ = 1 \lambda=1 λ=1, 即
w 1 ∗ = w 2 ∗ w_{1}^{*}=w_{2}^{*} w1∗=w2∗由此可以把两个最优解 ( w 1 ∗ , b 1 ∗ ) \left(w_{1}^{*}, b_{1}^{*}\right) (w1∗,b1∗) 和 ( w 2 ∗ , b 2 ∗ ) \left(w_{2}^{*}, b_{2}^{*}\right) (w2∗,b2∗) 分别写成 ( w ∗ , b 1 ∗ ) \left(w^{*}, b_{1}^{*}\right) (w∗,b1∗) 和 ( w ∗ , b 2 ∗ ) \left(w^{*}, b_{2}^{*}\right) (w∗,b2∗) 。
再证 b 1 ∗ = b 2 ∗ b_{1}^{*}=b_{2}^{*} b1∗=b2∗ 。设 x 1 ′ x_{1}^{\prime} x1′ 和 x 2 ′ x_{2}^{\prime} x2′ 是集合 { x i ∣ y i = + 1 } \left\{x_{i} \mid y_{i}=+1\right\} {xi∣yi=+1} 中分别对应于 ( w ∗ , b 1 ∗ ) \left(w^{*}, b_{1}^{*}\right) (w∗,b1∗) 和 ( w ∗ , b 2 ∗ ) \left(w^{*}, b_{2}^{*}\right) (w∗,b2∗) 使得问题的不等式等号成立的点, x 1 ′ ′ x_{1}^{\prime \prime} x1′′ 和 x 2 ′ ′ x_{2}^{\prime \prime} x2′′ 是集合 { x i ∣ y i = − 1 } \left\{x_{i} \mid y_{i}=-1\right\} {xi∣yi=−1} 中分别对应于 ( w ∗ , b 1 ∗ ) \left(w^{*}, b_{1}^{*}\right) (w∗,b1∗) 和 ( w ∗ , b 2 ∗ ) \left(w^{*}, b_{2}^{*}\right) (w∗,b2∗) 使得问题的不等式等号成立的点,∴ w ∗ ⋅ x 1 ′ + b 2 ∗ − 1 ⩾ 0 , w ∗ ⋅ x 2 ′ + b 2 ∗ − 1 = 0 = > w ∗ ⋅ x 1 ′ ≥ w ∗ ⋅ x 2 ′ w^{*} \cdot x_{1}^{\prime}+b_{2}^{*} -1\geqslant 0, \quad w^{*} \cdot x_{2}^{\prime}+b_{2}^{*} -1= 0=>w^{*} \cdot x_{1}^{\prime} \ge w^{*} \cdot x_{2}^{\prime} w∗⋅x1′+b2∗−1⩾0,w∗⋅x2′+b2∗−1=0=>w∗⋅x1′≥w∗⋅x2′ ; w ∗ ⋅ x 1 ′ + b 2 ∗ − 1 ⩾ 0 , w ∗ ⋅ x 2 ′ + b 2 ∗ − 1 = 0 = > w ∗ ⋅ x 1 ′ ≥ w ∗ ⋅ x 2 ′ w^{*} \cdot x_{1}^{\prime}+b_{2}^{*} -1\geqslant 0, \quad w^{*} \cdot x_{2}^{\prime}+b_{2}^{*} -1= 0=>w^{*} \cdot x_{1}^{\prime} \ge w^{*} \cdot x_{2}^{\prime} w∗⋅x1′+b2∗−1⩾0,w∗⋅x2′+b2∗−1=0=>w∗⋅x1′≥w∗⋅x2′,得出 w ∗ ⋅ ( x 1 ′ − x 2 ′ ) = 0 , w ∗ ⋅ ( x 1 ′ ′ − x 2 ′ ′ ) = 0 w^{*} \cdot\left(x_{1}^{\prime}-x_{2}^{\prime}\right)=0,w^{*} \cdot\left(x_{1}^{\prime \prime}-x_{2}^{\prime \prime}\right)=0 w∗⋅(x1′−x2′)=0,w∗⋅(x1′′−x2′′)=0,∴ x 1 ′ = x 2 ′ , x 1 ′ ′ = x 2 ′ ′ x_{1}^{\prime}=x_{2}^{\prime},x_{1}^{\prime \prime}=x_{2}^{\prime \prime} x1′=x2′,x1′′=x2′′
继续, w ∗ ⋅ x 1 ′ + b 1 ∗ − 1 = 0 , − [ w ∗ ⋅ x 1 ′ ′ + b 1 ∗ − 1 ] = 0 = > b 1 ∗ = − 1 2 ( w ∗ ⋅ x 1 ′ + w ∗ ⋅ x 1 ′ ′ ) w^{*} \cdot x_{1}^{\prime}+b_{1}^{*} -1= 0,-[w^{*} \cdot x_{1}^{{\prime}{\prime}}+b_{1}^{*} -1]= 0=>b_1^*=-\frac{1}{2}\left(w^{*} \cdot x_{1}^{\prime}+w^{*} \cdot x_{1}^{\prime \prime}\right) w∗⋅x1′+b1∗−1=0,−[w∗⋅x1′′+b1∗−1]=0=>b1∗=−21(w∗⋅x1′+w∗⋅x1′′),同理 b 2 ∗ = − 1 2 ( w ∗ ⋅ x 2 ′ + w ∗ ⋅ x 2 ′ ′ ) b_{2}^{*}=-\frac{1}{2}\left(w^{*} \cdot x_{2}^{\prime}+w^{*} \cdot x_{2}^{\prime \prime}\right) b2∗=−21(w∗⋅x2′+w∗⋅x2′′)=> b 1 ∗ = b 2 ∗ b_{1}^{*}=b_{2}^{*} b1∗=b2∗
-
-
支持向量和间隔边界
- 在线性可分情况下,训练数据集的样本点中与分离超平面距离最近的样本点的实例称为支持向量(support vector)。
- 支持向量是使约束条件式 y i ( w ⋅ x i + b ) − 1 ⩾ 0 , i = 1 , 2 , ⋯ , N y_{i}\left(w \cdot x_{i}+b\right)-1 \geqslant 0, \quad i=1,2, \cdots, N yi(w⋅xi+b)−1⩾0,i=1,2,⋯,N等号成立的点
-
H
1
H1
H1与
H
2
H2
H2之间的距离称为间隔(margin)。
间隔依赖于分离超平面的法向量 w w w , 等于 2 ∥ w ∥ \frac{2}{\|w\|} ∥w∥2 。 H 1 H_{1} H1 和 H 2 H_{2} H2 称 为间隔边界。
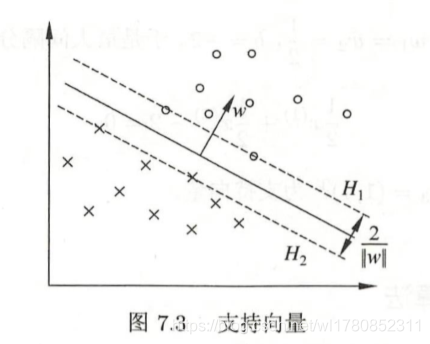
- 在线性可分情况下,训练数据集的样本点中与分离超平面距离最近的样本点的实例称为支持向量(support vector)。
7.1.4 学习的对偶算法
求解对偶问题的优点
- 对偶问题往往更容易求解;
- 自然引入核函数, 进而推广到非线性分类问题。
构建拉格朗日函数(Lagrange function)。为此, 对每一个不等式约束 y i ( w ⋅ x i + b ) − 1 ⩾ 0 , i = 1 , 2 , ⋯ , N y_{i}\left(w \cdot x_{i}+b\right)-1 \geqslant 0, \quad i=1,2, \cdots, N yi(w⋅xi+b)−1⩾0,i=1,2,⋯,N 引进拉格朗日乘子 (Lagrange multiplier) α i ⩾ 0 , i = 1 , 2 , ⋯ , N \alpha_{i} \geqslant 0, i=1,2, \cdots, N αi⩾0,i=1,2,⋯,N, 定义拉格朗日函数:
L ( w , b , α ) = 1 2 ∥ w ∥ 2 − ∑ i = 1 N α i y i ( w ⋅ x i + b ) + ∑ i = 1 N α i L(w, b, \alpha)=\frac{1}{2}\|w\|^{2}-\sum_{i=1}^{N} \alpha_{i} y_{i}\left(w \cdot x_{i}+b\right)+\sum_{i=1}^{N} \alpha_{i} L(w,b,α)=21∥w∥2−i=1∑Nαiyi(w⋅xi+b)+i=1∑Nαi
其中,
α
=
(
α
1
,
α
2
,
⋯
,
α
N
)
T
\alpha=\left(\alpha_{1}, \alpha_{2}, \cdots, \alpha_{N}\right)^{\mathrm{T}}
α=(α1,α2,⋯,αN)T 为拉格朗日乘子向量。
根据拉格朗日对偶性, 原始问题的对偶问题是极大极小问题:
max α min w , b L ( w , b , α ) \max _{\alpha} \min _{w, b} L(w, b, \alpha) αmaxw,bminL(w,b,α)
为了得到对偶问题的解, 需要先求
L
(
w
,
b
,
α
)
L(w, b, \alpha)
L(w,b,α) 对
w
,
b
w, b
w,b 的极小, 再求对
α
\alpha
α 的极大。
(1) 求
min
w
,
b
L
(
w
,
b
,
α
)
\min _{w, b} L(w, b, \alpha)
minw,bL(w,b,α)
将拉格朗日函数
L
(
w
,
b
,
α
)
L(w, b, \alpha)
L(w,b,α) 分别对
w
,
b
w, b
w,b 求偏导数并令其等于 0 。
∇ w L ( w , b , α ) = w − ∑ i = 1 N α i y i x i = 0 ∇ b L ( w , b , α ) = − ∑ i = 1 N α i y i = 0 \begin{aligned} &\nabla_{w} L(w, b, \alpha)=w-\sum_{i=1}^{N} \alpha_{i} y_{i} x_{i}=0 \\ &\nabla_{b} L(w, b, \alpha)=-\sum_{i=1}^{N} \alpha_{i} y_{i}=0 \end{aligned} ∇wL(w,b,α)=w−i=1∑Nαiyixi=0∇bL(w,b,α)=−i=1∑Nαiyi=0
得
w = ∑ i = 1 N α i y i x i w=\sum_{i=1}^{N} \alpha_{i} y_{i} x_{i} w=i=1∑Nαiyixi
∑ i = 1 N α i y i = 0 \sum_{i=1}^{N} \alpha_{i} y_{i}=0 i=1∑Nαiyi=0
将式 w = ∑ i = 1 N α i y i x i w=\sum_{i=1}^{N} \alpha_{i} y_{i} x_i w=∑i=1Nαiyixi代入拉格朗日函数 L ( w , b , α ) = 1 2 ∥ w ∥ 2 − ∑ i = 1 N α i y i ( w ⋅ x i + b ) + ∑ i = 1 N α i L(w, b, \alpha)=\frac{1}{2}\|w\|{2}-\sum_{i=1}{N} \alpha_{i} y_{i}\left(w \cdot x_{i}+b\right)+\sum_{i=1}^{N} \alpha_{i} L(w,b,α)=21∥w∥2−∑i=1Nαiyi(w⋅xi+b)+∑i=1Nαi, 并利用式 ∑ i = 1 N α i y i = 0 \sum_{i=1}^{N} \alpha_{i} y_{i}=0 ∑i=1Nαiyi=0, 即得
L ( w , b , α ) = 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i y i ( ( ∑ j = 1 N α j y j x j ) ⋅ x i + b ) + ∑ i = 1 N α i = 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − b ∑ i = 1 N α i y i + ∑ i = 1 N α i = 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − 0 + ∑ i = 1 N α i = − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) + ∑ i = 1 N α i \begin{aligned} L(w, b, \alpha) &=\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} y_{i}\left(\left(\sum_{j=1}^{N} \alpha_{j} y_{j} x_{j}\right) \cdot x_{i}+b\right)+\sum_{i=1}^{N} \alpha_{i} \\ &=\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-\sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-b\sum_{i=1}^{N} \alpha_{i} y_{i}+\sum_{i=1}^{N} \alpha_{i} \\ &=\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-\sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-0+\sum_{i=1}^{N} \alpha_{i} \\ &=-\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)+\sum_{i=1}^{N} \alpha_{i} \end{aligned} L(w,b,α)=21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nαiyi((j=1∑Nαjyjxj)⋅xi+b)+i=1∑Nαi=21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−bi=1∑Nαiyi+i=1∑Nαi=21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−0+i=1∑Nαi=−21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)+i=1∑Nαi
即
min w , b L ( w , b , α ) = − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) + ∑ i = 1 N α i \min _{w, b} L(w, b, \alpha)=-\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)+\sum_{i=1}^{N} \alpha_{i} w,bminL(w,b,α)=−21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)+i=1∑Nαi
(2) 求 min w , b L ( w , b , α ) \min _{w, b} L(w, b, \alpha) minw,bL(w,b,α) 对 α \alpha α 的极大, 即是对偶问题
max α − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) + ∑ i = 1 N α i s.t. ∑ i = 1 N α i y i = 0 α i ⩾ 0 , i = 1 , 2 , ⋯ , N \begin{array}{ll} \max _{\alpha} & -\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)+\sum_{i=1}^{N} \alpha_{i} \\ \text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\ & \alpha_{i} \geqslant 0, \quad i=1,2, \cdots, N \end{array} maxα s.t. −21∑i=1N∑j=1Nαiαjyiyj(xi⋅xj)+∑i=1Nαi∑i=1Nαiyi=0αi⩾0,i=1,2,⋯,N
将式 max α a m p ; − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) + ∑ i = 1 N α i s.t. a m p ; ∑ i = 1 N α i y i = 0 a m p ; α i ⩾ 0 , i = 1 , 2 , ⋯ , N \begin{array}{ll}\max _{\alpha} & -\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)+\sum_{i=1}^{N} \alpha_{i} \\\text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\& \alpha_{i} \geqslant 0, \quad i=1,2, \cdots, N\end{array} maxα s.t. amp;−21∑i=1N∑j=1Nαiαjyiyj(xi⋅xj)+∑i=1Nαiamp;∑i=1Nαiyi=0amp;αi⩾0,i=1,2,⋯,N 的目标函数由求极大转换成求极小, 就得到下面与之等价的对偶最优化问题:
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i s.t. ∑ i = 1 N α i y i = 0 α i ⩾ 0 , i = 1 , 2 , ⋯ , N \begin{array}{ll} \min _{\alpha} & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} \\ \text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\ & \alpha_{i} \geqslant 0, \quad i=1,2, \cdots, N \end{array} minα s.t. 21∑i=1N∑j=1Nαiαjyiyj(xi⋅xj)−∑i=1Nαi∑i=1Nαiyi=0αi⩾0,i=1,2,⋯,N
这个最优化问题可以求解出最优解 α ∗ \alpha^* α∗
设
α
∗
=
(
α
1
∗
,
α
2
∗
,
⋯
,
α
l
∗
)
T
\alpha^{*}=\left(\alpha_{1}^{*}, \alpha_{2}^{*}, \cdots, \alpha_{l}^{*}\right)^{\mathrm{T}}
α∗=(α1∗,α2∗,⋯,αl∗)T 是对偶最优化问题
min
α
1
2
∑
i
=
1
N
∑
j
=
1
N
α
i
α
j
y
i
y
j
(
x
i
⋅
x
j
)
−
∑
i
=
1
N
α
i
s.t.
∑
i
=
1
N
α
i
y
i
=
0
α
i
⩾
0
,
i
=
1
,
2
,
⋯
,
N
\begin{array}{ll}\min _{\alpha} & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} \\\text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\& \alpha_{i} \geqslant 0, \quad i=1,2, \cdots, N\end{array}
minα s.t. 21∑i=1N∑j=1Nαiαjyiyj(xi⋅xj)−∑i=1Nαi∑i=1Nαiyi=0αi⩾0,i=1,2,⋯,N 的解, 则
存在下标
j
j
j, 使得
α
j
∗
>
0
\alpha_{j}^{*}>0
αj∗>0, 并可按下式求得原始最优化问题
min
w
,
b
1
2
∥
w
∥
2
s.t.
y
i
(
w
⋅
x
i
+
b
)
−
1
⩾
0
,
i
=
1
,
2
,
⋯
,
N
\begin{array}{ll}\min _{w, b} & \frac{1}{2}\|w\|^{2} \\\text { s.t. } & y_{i}\left(w \cdot x_{i}+b\right)-1 \geqslant 0, \quad i=1,2, \cdots, N\end{array}
minw,b s.t. 21∥w∥2yi(w⋅xi+b)−1⩾0,i=1,2,⋯,N 的解
w
∗
,
b
∗
w^{*}, b^{*}
w∗,b∗ :
w ∗ = ∑ i = 1 N α i ∗ y i x i b ∗ = y j − ∑ i = 1 N α i ∗ y i ( x i ⋅ x j ) \begin{gathered} w^{*}=\sum_{i=1}^{N} \alpha_{i}^{*} y_{i} x_{i} \\ b^{*}=y_{j}-\sum_{i=1}^{N} \alpha_{i}^{*} y_{i}\left(x_{i} \cdot x_{j}\right) \end{gathered} w∗=i=1∑Nαi∗yixib∗=yj−i=1∑Nαi∗yi(xi⋅xj)
证明 KKT 条件成立, 即得
∇ w L ( w ∗ , b ∗ , α ∗ ) = w ∗ − ∑ i = 1 N α i ∗ y i x i = 0 \nabla_{w} L\left(w^{*}, b^{*}, \alpha^{*}\right)=w^{*}-\sum_{i=1}^{N} \alpha_{i}^{*} y_{i} x_{i}=0 ∇wL(w∗,b∗,α∗)=w∗−i=1∑Nαi∗yixi=0
∇ b L ( w ∗ , b ∗ , α ∗ ) = − ∑ i = 1 N α i ∗ y i = 0 α i ∗ ( y i ( w ∗ ⋅ x i + b ∗ ) − 1 ) = 0 , i = 1 , 2 , ⋯ , N y i ( w ∗ ⋅ x i + b ∗ ) − 1 ⩾ 0 , i = 1 , 2 , ⋯ , N α i ∗ ⩾ 0 , i = 1 , 2 , ⋯ , N \begin{aligned} &\nabla_{b} L\left(w^{*}, b^{*}, \alpha^{*}\right)=-\sum_{i=1}^{N} \alpha_{i}^{*} y_{i}=0 \\ &\alpha_{i}^{*}\left(y_{i}\left(w^{*} \cdot x_{i}+b^{*}\right)-1\right)=0, \quad i=1,2, \cdots, N \\ &y_{i}\left(w^{*} \cdot x_{i}+b^{*}\right)-1 \geqslant 0, \quad i=1,2, \cdots, N \\ &\alpha_{i}^{*} \geqslant 0, \quad i=1,2, \cdots, N \end{aligned} ∇bL(w∗,b∗,α∗)=−i=1∑Nαi∗yi=0αi∗(yi(w∗⋅xi+b∗)−1)=0,i=1,2,⋯,Nyi(w∗⋅xi+b∗)−1⩾0,i=1,2,⋯,Nαi∗⩾0,i=1,2,⋯,N
由此得
w ∗ = ∑ i α i ∗ y i x i w^{*}=\sum_{i} \alpha_{i}^{*} y_{i} x_{i} w∗=i∑αi∗yixi
其中至少有一个 α j ∗ > 0 \alpha_{j}^{*}>0 αj∗>0 (用反证法, 假设 α ∗ = 0 \alpha^{*}=0 α∗=0, 由式 ∇ w L ( w ∗ , b ∗ , α ∗ ) = w ∗ − ∑ i = 1 N α i ∗ y i x i = 0 \nabla_{w} L\left(w^{*}, b^{*}, \alpha^{*}\right)=w^{*}-\sum_{i=1}^{N} \alpha_{i}^{*} y_{i} x_{i}=0 ∇wL(w∗,b∗,α∗)=w∗−∑i=1Nαi∗yixi=0 可知 w ∗ = 0 w^{*}=0 w∗=0, 而 w ∗ = 0 w^{*}=0 w∗=0 不是原始最优化问题 min w , b 1 2 ∥ w ∥ 2 s.t. y i ( w ⋅ x i + b ) − 1 ⩾ 0 , i = 1 , 2 , ⋯ , N \begin{array}{ll}\min _{w, b} & \frac{1}{2}\|w\|^{2} \\\text { s.t. } & y_{i}\left(w \cdot x_{i}+b\right)-1 \geqslant 0, \quad i=1,2, \cdots, N\end{array} minw,b s.t. 21∥w∥2yi(w⋅xi+b)−1⩾0,i=1,2,⋯,N 的解, 产生矛盾), 对此 j j j 有
y j ( w ∗ ⋅ x j + b ∗ ) − 1 = 0 y_{j}\left(w^{*} \cdot x_{j}+b^{*}\right)-1=0 yj(w∗⋅xj+b∗)−1=0
将式 w ∗ = ∑ i = 1 N α i ∗ y i x i w^{*}=\sum_{i=1}^{N} \alpha_{i}^{*} y_{i} x_{i} w∗=∑i=1Nαi∗yixi 代入式 y j ( w ∗ ⋅ x j + b ∗ ) − 1 = 0 y_{j}\left(w^{*} \cdot x_{j}+b^{*}\right)-1=0 yj(w∗⋅xj+b∗)−1=0 并注意到 y j 2 = 1 y_{j}^{2}=1 yj2=1, 即得
b ∗ = y j − ∑ i = 1 N α i ∗ y i ( x i ⋅ x j ) b^{*}=y_{j}-\sum_{i=1}^{N} \alpha_{i}^{*} y_{i}\left(x_{i} \cdot x_{j}\right) b∗=yj−i=1∑Nαi∗yi(xi⋅xj)
由此定理可知, 分离超平面可以写成
∑ i = 1 N α i ∗ y i ( x ⋅ x i ) + b ∗ = 0 \sum_{i=1}^{N} \alpha_{i}^{*} y_{i}\left(x \cdot x_{i}\right)+b^{*}=0 i=1∑Nαi∗yi(x⋅xi)+b∗=0
分类决策函数可以写成
f ( x ) = sign ( ∑ i = 1 N α i ∗ y i ( x ⋅ x i ) + b ∗ ) f(x)=\operatorname{sign}\left(\sum_{i=1}^{N} \alpha_{i}^{*} y_{i}\left(x \cdot x_{i}\right)+b^{*}\right) f(x)=sign(i=1∑Nαi∗yi(x⋅xi)+b∗)
线性可分支持向量机学习算法 输入:线性可分训练集
T
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
⋯
,
(
x
N
,
y
N
)
}
T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{N}, y_{N}\right)\right\}
T={(x1,y1),(x2,y2),⋯,(xN,yN)}, 其中
x
i
∈
X
=
R
n
x_{i} \in \mathcal{X}=\mathbf{R}^{n}
xi∈X=Rn,
y
i
∈
Y
=
{
−
1
,
+
1
}
,
i
=
1
,
2
,
⋯
,
N
y_{i} \in \mathcal{Y}=\{-1,+1\}, i=1,2, \cdots, N
yi∈Y={−1,+1},i=1,2,⋯,N
输出:分离超平面和分类决策函数。
-
构造并求解约束最优化问题
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i s.t. ∑ i = 1 N α i y i = 0 α i ⩾ 0 , i = 1 , 2 , ⋯ , N \begin{array}{ll} \min _{\alpha} & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} \\ \text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\ & \alpha_{i} \geqslant 0, \quad i=1,2, \cdots, N \end{array} minα s.t. 21∑i=1N∑j=1Nαiαjyiyj(xi⋅xj)−∑i=1Nαi∑i=1Nαiyi=0αi⩾0,i=1,2,⋯,N求得最优解 α ∗ = ( α 1 ∗ , α 2 ∗ , ⋯ , α N ∗ ) T \alpha^{*}=\left(\alpha_{1}^{*}, \alpha_{2}^{*}, \cdots, \alpha_{N}^{*}\right)^{\mathrm{T}} α∗=(α1∗,α2∗,⋯,αN∗)T 。
-
计算
w ∗ = ∑ i = 1 N α i ∗ y i x i w^{*}=\sum_{i=1}^{N} \alpha_{i}^{*} y_{i} x_{i} w∗=i=1∑Nαi∗yixi并选择 α ∗ \alpha^{*} α∗ 的一个正分量 α j ∗ > 0 \alpha_{j}^{*}>0 αj∗>0, 计算
b ∗ = y j − ∑ i = 1 N α i ∗ y i ( x i ⋅ x j ) b^{*}=y_{j}-\sum_{i=1}^{N} \alpha_{i}^{*} y_{i}\left(x_{i} \cdot x_{j}\right) b∗=yj−i=1∑Nαi∗yi(xi⋅xj) -
求得分离超平面
w ∗ ⋅ x + b ∗ = 0 w^{*} \cdot x+b^{*}=0 w∗⋅x+b∗=0分类决策函数:
f ( x ) = sign ( w ∗ ⋅ x + b ∗ ) f(x)=\operatorname{sign}\left(w^{*} \cdot x+b^{*}\right) f(x)=sign(w∗⋅x+b∗)在线性可分支持向量机中, 由式 w ∗ = ∑ i = 1 N α i ∗ y i x i w^{*}=\sum_{i=1}^{N} \alpha_{i}^{*} y_{i} x_{i} w∗=∑i=1Nαi∗yixi 、式 b ∗ = y j − ∑ i = 1 N α i ∗ y i ( x i ⋅ x j ) b^{*}=y_{j}-\sum_{i=1}^{N} \alpha_{i}^{*} y_{i}\left(x_{i} \cdot x_{j}\right) b∗=yj−∑i=1Nαi∗yi(xi⋅xj) 可知, w ∗ w^{*} w∗ 和 b ∗ b^{*} b∗ 只依赖于训练数据中对应于 α i ∗ > 0 \alpha_{i}^{*}>0 αi∗>0 的样本点 ( x i , y i ) \left(x_{i}, y_{i}\right) (xi,yi), 而其他样本点对 w ∗ w^{*} w∗ 和 b ∗ b^{*} b∗ 没有影响。训练数据中对应于 α i ∗ > 0 \alpha_{i}^{*}>0 αi∗>0 的实例点 x i ∈ R n x_{i} \in \mathbf{R}^{n} xi∈Rn 称为支持向量。
支持向量
考虑原始最优化问题及对偶最优化问题, 将训练数据集中对应于 α i ∗ > 0 \alpha_{i}^{*}>0 αi∗>0 的样本点 ( x i , y i ) \left(x_{i}, y_{i}\right) (xi,yi) 的实例 x i ∈ R n x_{i} \in \mathbf{R}^{n} xi∈Rn 称为 支持向量。
根据这一定义, 支持向量一定在间隔边界上。由 KKT 互补条件可知,α i ∗ ( y i ( w ∗ ⋅ x i + b ∗ ) − 1 ) = 0 , i = 1 , 2 , ⋯ , N \alpha_{i}^{*}\left(y_{i}\left(w^{*} \cdot x_{i}+b^{*}\right)-1\right)=0, \quad i=1,2, \cdots, N αi∗(yi(w∗⋅xi+b∗)−1)=0,i=1,2,⋯,N
对应于 α i ∗ > 0 \alpha_{i}^{*}>0 αi∗>0 的实例 x i x_{i} xi, 有
y i ( w ∗ ⋅ x i + b ∗ ) − 1 = 0 y_{i}\left(w^{*} \cdot x_{i}+b^{*}\right)-1=0 yi(w∗⋅xi+b∗)−1=0
或
w ∗ ⋅ x i + b ∗ = ± 1 w^{*} \cdot x_{i}+b^{*}=\pm 1 w∗⋅xi+b∗=±1
即 x i x_{i} xi 一定在间隔边界上。这里的支持向量的定义与前面给出的支持向量的定义是一致的。
备注:在间隔边界上 α i ∗ \alpha_i^* αi∗>0,表现为置信度高,所以叫支持向量。其余的实例点 α i ∗ \alpha_i^* αi∗=0
7.2 线性支持向量机与软间隔最大化
7.2.1线性支持向量机
-
线性不可分问题
线性不可分意味着某些样本点 ( x i , y i ) \left(x_{i}, y_{i}\right) (xi,yi) 不能满足函数间隔大于等于 1 的约束条件 y i ( w ⋅ x i + b ) − 1 ⩾ 0 , i = 1 , 2 , ⋯ , N y_{i}\left(w \cdot x_{i}+b\right)-1 \geqslant 0, \quad i=1,2, \cdots, N yi(w⋅xi+b)−1⩾0,i=1,2,⋯,N。 可以对每个样本点 ( x i , y i ) \left(x_{i}, y_{i}\right) (xi,yi) 引进一个松弛变量 ξ i ⩾ 0 \xi_{i} \geqslant 0 ξi⩾0, 使函数间隔加上松弛变量大于等于 1 。 这样, 约束条件变为
y i ( w ⋅ x i + b ) ⩾ 1 − ξ i y_{i}\left(w \cdot x_{i}+b\right) \geqslant 1-\xi_{i} yi(w⋅xi+b)⩾1−ξi同时, 对每个松弛变量 ξ i \xi_{i} ξi, 支付一个代价 ξ i \xi_{i} ξi 。目标函数由原来的 1 2 ∥ w ∥ 2 \frac{1}{2}\|w\|^{2} 21∥w∥2 变成
1 2 ∥ w ∥ 2 + C ∑ i = 1 N ξ i \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{N} \xi_{i} 21∥w∥2+Ci=1∑NξiC > 0 C>0 C>0 称为惩罚参数, 一般由应用问题决定, C C C 值大时对误分类的惩罚增大, C C C 值小时对误分类的怤罚减小。最小化目标函数 1 2 ∥ w ∥ 2 + C ∑ i = 1 N ξ i \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{N} \xi_{i} 21∥w∥2+C∑i=1Nξi 包含两层含义: 使 1 2 ∥ w ∥ 2 \frac{1}{2}\|w\|^{2} 21∥w∥2 尽量小即间隔尽量大, 同时使误分类点的个数尽量小, C C C 是调和二者的系数。
软间隔最大化:训练数据集线性不可分时的线性支持向量机学习问题。
线性不可分的线性支持向量机的学习问题变成如下凸二次规划 (convex quadratic programming ) 问题 (原始问题):
min w , b , ξ 1 2 ∥ w ∥ 2 + C ∑ i = 1 N ξ i s.t. y i ( w ⋅ x i + b ) ⩾ 1 − ξ i , i = 1 , 2 , ⋯ , N ξ i ⩾ 0 , i = 1 , 2 , ⋯ , N \begin{array}{ll} \min _{w, b, \xi} & \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{N} \xi_{i} \\ \text { s.t. } & y_{i}\left(w \cdot x_{i}+b\right) \geqslant 1-\xi_{i}, \quad i=1,2, \cdots, N \\ & \xi_{i} \geqslant 0, \quad i=1,2, \cdots, N \end{array} minw,b,ξ s.t. 21∥w∥2+C∑i=1Nξiyi(w⋅xi+b)⩾1−ξi,i=1,2,⋯,Nξi⩾0,i=1,2,⋯,N -
线性支持向量机 对于给定的线性不可分的训练数据集, 通过求解凸二次规划问题, 即软间隔最大化问题, 得到的分离超平面为
w ∗ ⋅ x + b ∗ = 0 w^{*} \cdot x+b^{*}=0 w∗⋅x+b∗=0以及相应的分类决策函数
f ( x ) = sign ( w ∗ ⋅ x + b ∗ ) f(x)=\operatorname{sign}\left(w^{*} \cdot x+b^{*}\right) f(x)=sign(w∗⋅x+b∗)称为线性支持向量机。
7.2.2 学习的对偶算法
原始问题 min w , b , ξ 1 2 ∥ w ∥ 2 + C ∑ i = 1 N ξ i s.t. y i ( w ⋅ x i + b ) ⩾ 1 − ξ i , i = 1 , 2 , ⋯ , N ξ i ⩾ 0 , i = 1 , 2 , ⋯ , N \begin{array}{ll}\min _{w, b, \xi} & \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{N} \xi_{i} \\\text { s.t. } & y_{i}\left(w \cdot x_{i}+b\right) \geqslant 1-\xi_{i}, \quad i=1,2, \cdots, N \\& \xi_{i} \geqslant 0, \quad i=1,2, \cdots, N\end{array} minw,b,ξ s.t. 21∥w∥2+C∑i=1Nξiyi(w⋅xi+b)⩾1−ξi,i=1,2,⋯,Nξi⩾0,i=1,2,⋯,N 的对偶问题是
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i s.t. ∑ i = 1 N α i y i = 0 0 ⩽ α i ⩽ C , i = 1 , 2 , ⋯ , N \begin{array}{ll} \min _{\alpha} & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} \\ \text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\ & 0 \leqslant \alpha_{i} \leqslant C, \quad i=1,2, \cdots, N \end{array} minα s.t. 21∑i=1N∑j=1Nαiαjyiyj(xi⋅xj)−∑i=1Nαi∑i=1Nαiyi=00⩽αi⩽C,i=1,2,⋯,N
推导过程:
原始最优化问题的拉格朗日函数是
L ( w , b , ξ , α , μ ) ≡ 1 2 ∥ w ∥ 2 + C ∑ i = 1 N ξ i − ∑ i = 1 N α i ( y i ( w ⋅ x i + b ) − 1 + ξ i ) − ∑ i = 1 N μ i ξ i L(w, b, \xi, \alpha, \mu) \equiv \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{N} \xi_{i}-\sum_{i=1}^{N} \alpha_{i}\left(y_{i}\left(w \cdot x_{i}+b\right)-1+\xi_{i}\right)-\sum_{i=1}^{N} \mu_{i} \xi_{i} L(w,b,ξ,α,μ)≡21∥w∥2+Ci=1∑Nξi−i=1∑Nαi(yi(w⋅xi+b)−1+ξi)−i=1∑Nμiξi
其中, α i ⩾ 0 , μ i ⩾ 0 \alpha_{i} \geqslant 0, \mu_{i} \geqslant 0 αi⩾0,μi⩾0 。
对偶问题是拉格朗日函数的极大极小问题。首先求 L ( w , b , ξ , α , μ ) L(w, b, \xi, \alpha, \mu) L(w,b,ξ,α,μ) 对 w , b , ξ w, b, \xi w,b,ξ 的极小, 由∇ w L ( w , b , ξ , α , μ ) = w − ∑ i = 1 N α i y i x i = 0 ∇ b L ( w , b , ξ , α , μ ) = − ∑ i = 1 N α i y i = 0 ∇ ξ 1 L ( w , b , ξ , α , μ ) = C − α i − μ i = 0 \begin{aligned} &\nabla_{w} L(w, b, \xi, \alpha, \mu)=w-\sum_{i=1}^{N} \alpha_{i} y_{i} x_{i}=0 \\ &\nabla_{b} L(w, b, \xi, \alpha, \mu)=-\sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\ &\nabla_{\xi_{1}} L(w, b, \xi, \alpha, \mu)=C-\alpha_{i}-\mu_{i}=0 \end{aligned} ∇wL(w,b,ξ,α,μ)=w−i=1∑Nαiyixi=0∇bL(w,b,ξ,α,μ)=−i=1∑Nαiyi=0∇ξ1L(w,b,ξ,α,μ)=C−αi−μi=0
得
w = ∑ i = 1 N α i y i x i w=\sum_{i=1}^{N} \alpha_{i} y_{i} x_{i} w=i=1∑Nαiyixi
∑ i = 1 N α i y i = 0 C − α i − μ i = 0 \begin{gathered} \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\ C-\alpha_{i}-\mu_{i}=0 \end{gathered} i=1∑Nαiyi=0C−αi−μi=0
将上面三个式子代入式 L ( w , b , ξ , α , μ ) ≡ 1 2 ∥ w ∥ 2 + C ∑ i = 1 N ξ i − ∑ i = 1 N α i ( y i ( w ⋅ x i + b ) − 1 + ξ i ) − ∑ i = 1 N μ i ξ i L(w, b, \xi, \alpha, \mu) \equiv \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{N} \xi_{i}-\sum_{i=1}^{N} \alpha_{i}\left(y_{i}\left(w \cdot x_{i}+b\right)-1+\xi_{i}\right)-\sum_{i=1}^{N} \mu_{i} \xi_{i} L(w,b,ξ,α,μ)≡21∥w∥2+C∑i=1Nξi−∑i=1Nαi(yi(w⋅xi+b)−1+ξi)−∑i=1Nμiξi, 得
min w , b , ξ L ( w , b , ξ , α , μ ) = − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) + ∑ i = 1 N α i \min _{w, b, \xi} L(w, b, \xi, \alpha, \mu)=-\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)+\sum_{i=1}^{N} \alpha_{i} w,b,ξminL(w,b,ξ,α,μ)=−21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)+i=1∑Nαi
再对 min w , b , ξ L ( w , b , ξ , α , μ ) \min _{w, b, \xi} L(w, b, \xi, \alpha, \mu) minw,b,ξL(w,b,ξ,α,μ) 求 α \alpha α 的极大, 即得对偶问题:
max α − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) + ∑ i = 1 N α i s.t. ∑ i = 1 N α i y i = 0 C − α i − μ i = 0 α i ⩾ 0 μ i ⩾ 0 , i = 1 , 2 , ⋯ , N \begin{array}{ll} \max _{\alpha} & -\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)+\sum_{i=1}^{N} \alpha_{i} \\ \text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\ & C-\alpha_{i}-\mu_{i}=0 \\ & \alpha_{i} \geqslant 0 \\ & \mu_{i} \geqslant 0, \quad i=1,2, \cdots, N \end{array} maxα s.t. −21∑i=1N∑j=1Nαiαjyiyj(xi⋅xj)+∑i=1Nαi∑i=1Nαiyi=0C−αi−μi=0αi⩾0μi⩾0,i=1,2,⋯,N
C − α i − μ i = 0 = > C − α i = μ i , ∵ μ i ⩾ 0 , ∴ C − α i = μ i ⩾ 0 , = > α i ⩽ C , 又 ∵ α i ⩾ 0 , ∴ C-\alpha_{i}-\mu_{i}=0=>C-\alpha_{i}=\mu_{i},∵\mu_{i} \geqslant 0 ,∴C-\alpha_{i}=\mu_{i} \geqslant 0 ,=>\alpha_{i} \leqslant C,又∵\alpha_{i} \geqslant 0,∴ C−αi−μi=0=>C−αi=μi,∵μi⩾0,∴C−αi=μi⩾0,=>αi⩽C,又∵αi⩾0,∴
0 ⩽ α i ⩽ C 0 \leqslant \alpha_{i} \leqslant C 0⩽αi⩽C
再将对目标函数求极大转换为求极小, 于是得到对偶问题 min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i s.t. ∑ i = 1 N α i y i = 0 0 ⩽ α i ⩽ C , i = 1 , 2 , ⋯ , N \begin{array}{ll}\min _{\alpha} & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} \\\text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\& 0 \leqslant \alpha_{i} \leqslant C, \quad i=1,2, \cdots, N\end{array} minα s.t. 21∑i=1N∑j=1Nαiαjyiyj(xi⋅xj)−∑i=1Nαi∑i=1Nαiyi=00⩽αi⩽C,i=1,2,⋯,N 。 可以通过求解对偶问题而得到原始问题的解, 进而确定分离超平面和决策函数。 为此, 就可以定理的形式叙述原始问题的最优解和对偶问题的最优解的关系。
对目标函数求极大转换为求极小, 得到对偶问题。 可以通过求解对偶问题而得到原始问题的解, 进而确定分离超平面和决策函数。
设
α
∗
=
(
α
1
∗
,
α
2
∗
,
⋯
,
α
N
∗
)
T
\alpha^{*}=\left(\alpha_{1}^{*}, \alpha_{2}^{*}, \cdots, \alpha_{N}^{*}\right)^{\mathrm{T}}
α∗=(α1∗,α2∗,⋯,αN∗)T 是对偶问题
min
α
1
2
∑
i
=
1
N
∑
j
=
1
N
α
i
α
j
y
i
y
j
(
x
i
⋅
x
j
)
−
∑
i
=
1
N
α
i
s.t.
∑
i
=
1
N
α
i
y
i
=
0
0
⩽
α
i
⩽
C
,
i
=
1
,
2
,
⋯
,
N
\begin{array}{ll}\min _{\alpha} & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} \\\text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\& 0 \leqslant \alpha_{i} \leqslant C, \quad i=1,2, \cdots, N\end{array}
minα s.t. 21∑i=1N∑j=1Nαiαjyiyj(xi⋅xj)−∑i=1Nαi∑i=1Nαiyi=00⩽αi⩽C,i=1,2,⋯,N 的一个解, 若存
在 α ∗ \alpha^{*} α∗ 的一个分量 α j ∗ , 0 < α j ∗ < C \alpha_{j}^{*}, 0<\alpha_{j}^{*}<C αj∗,0<αj∗<C, 则原始问题 min w , b , ξ 1 2 ∥ w ∥ 2 + C ∑ i = 1 N ξ i s.t. y i ( w ⋅ x i + b ) ⩾ 1 − ξ i , i = 1 , 2 , ⋯ , N ξ i ⩾ 0 , i = 1 , 2 , ⋯ , N \begin{array}{ll}\min _{w, b, \xi} & \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{N} \xi_{i} \\\text { s.t. } & y_{i}\left(w \cdot x_{i}+b\right) \geqslant 1-\xi_{i}, \quad i=1,2, \cdots, N \\& \xi_{i} \geqslant 0, \quad i=1,2, \cdots, N\end{array} minw,b,ξ s.t. 21∥w∥2+C∑i=1Nξiyi(w⋅xi+b)⩾1−ξi,i=1,2,⋯,Nξi⩾0,i=1,2,⋯,N 的解 w ∗ , b ∗ w^{*}, b^{*} w∗,b∗ 可按下式 求得:
w ∗ = ∑ i = 1 N α i ∗ y i x i b ∗ = y j − ∑ i = 1 N y i α i ∗ ( x i ⋅ x j ) \begin{gathered} w^{*}=\sum_{i=1}^{N} \alpha_{i}^{*} y_{i} x_{i} \\ b^{*}=y_{j}-\sum_{i=1}^{N} y_{i} \alpha_{i}^{*}\left(x_{i} \cdot x_{j}\right) \end{gathered} w∗=i=1∑Nαi∗yixib∗=yj−i=1∑Nyiαi∗(xi⋅xj)
证明 原始问题是凸二次规划问题, 解满足 KKT 条件。即得
∇ w L ( w ∗ , b ∗ , ξ ∗ , α ∗ , μ ∗ ) = w ∗ − ∑ i = 1 N α i ∗ y i x i = 0 \nabla_{w} L\left(w^{*}, b^{*}, \xi^{*}, \alpha^{*}, \mu^{*}\right)=w^{*}-\sum_{i=1}^{N} \alpha_{i}^{*} y_{i} x_{i}=0 ∇wL(w∗,b∗,ξ∗,α∗,μ∗)=w∗−i=1∑Nαi∗yixi=0
∇ b L ( w ∗ , b ∗ , ξ ∗ , α ∗ , μ ∗ ) = − ∑ i = 1 N α i ∗ y i = 0 ∇ ξ L ( w ∗ , b ∗ , ξ ∗ , α ∗ , μ ∗ ) = C − α ∗ − μ ∗ = 0 α i ∗ ( y i ( w ∗ ⋅ x i + b ∗ ) − 1 + ξ i ∗ ) = 0 μ i ∗ ξ i ∗ = 0 \begin{gathered} \nabla_{b} L\left(w^{*}, b^{*}, \xi^{*}, \alpha^{*}, \mu^{*}\right)=-\sum_{i=1}^{N} \alpha_{i}^{*} y_{i}=0 \\ \nabla_{\xi} L\left(w^{*}, b^{*}, \xi^{*}, \alpha^{*}, \mu^{*}\right)=C-\alpha^{*}-\mu^{*}=0 \\ \alpha_{i}^{*}\left(y_{i}\left(w^{*} \cdot x_{i}+b^{*}\right)-1+\xi_{i}^{*}\right)=0 \\ \mu_{i}^{*} \xi_{i}^{*}=0 \end{gathered} ∇bL(w∗,b∗,ξ∗,α∗,μ∗)=−i=1∑Nαi∗yi=0∇ξL(w∗,b∗,ξ∗,α∗,μ∗)=C−α∗−μ∗=0αi∗(yi(w∗⋅xi+b∗)−1+ξi∗)=0μi∗ξi∗=0
y i ( w ∗ ⋅ x i + b ∗ ) − 1 + ξ i ∗ ⩾ 0 ξ i ∗ ⩾ 0 α i ∗ ⩾ 0 μ i ∗ ⩾ 0 , i = 1 , 2 , ⋯ , N \begin{gathered} y_{i}\left(w^{*} \cdot x_{i}+b^{*}\right)-1+\xi_{i}^{*} \geqslant 0 \\ \xi_{i}^{*} \geqslant 0 \\ \alpha_{i}^{*} \geqslant 0 \\ \mu_{i}^{*} \geqslant 0, \quad i=1,2, \cdots, N \end{gathered} yi(w∗⋅xi+b∗)−1+ξi∗⩾0ξi∗⩾0αi∗⩾0μi∗⩾0,i=1,2,⋯,N
由式 ∇ w L ( w ∗ , b ∗ , ξ ∗ , α ∗ , μ ∗ ) = w ∗ − ∑ i = 1 N α i ∗ y i x i = 0 \nabla_{w} L\left(w^{*}, b^{*}, \xi^{*}, \alpha^{*}, \mu^{*}\right)=w^{*}-\sum_{i=1}^{N} \alpha_{i}^{*} y_{i} x_{i}=0 ∇wL(w∗,b∗,ξ∗,α∗,μ∗)=w∗−∑i=1Nαi∗yixi=0 易知式 w ∗ = ∑ i = 1 N α i ∗ y i x i w^{*}=\sum_{i=1}^{N} \alpha_{i}^{*} y_{i} x_{i} w∗=∑i=1Nαi∗yixi 成立。再由式 α i ∗ ( y i ( w ∗ ⋅ x i + b ∗ ) − 1 + ξ i ∗ ) = 0 μ i ∗ ξ i ∗ = 0 \alpha_{i}^{*}\left(y_{i}\left(w^{*} \cdot x_{i}+b^{*}\right)-1+\xi_{i}^{*}\right)=0 \\\mu_{i}^{*} \xi_{i}^{*}=0 αi∗(yi(w∗⋅xi+b∗)−1+ξi∗)=0μi∗ξi∗=0 可知, 若存在 α j ∗ , 0 < α j ∗ < \alpha_{j}^{*}, 0<\alpha_{j}^{*}< αj∗,0<αj∗< C C C, 则 y i ( w ∗ ⋅ x i + b ∗ ) − 1 = 0 y_{i}\left(w^{*} \cdot x_{i}+b^{*}\right)-1=0 yi(w∗⋅xi+b∗)−1=0 。 y i ( w ∗ ⋅ x i + b ∗ ) − 1 = 0 = > y i ( w ∗ ⋅ x i + b ∗ ) − y j 2 = 0 = > w ∗ ⋅ x i + b ∗ − y j = 0 = > b ∗ = y j − ∑ i = 1 N y i α i ∗ ( x i ⋅ x j ) y_{i}\left(w^{*} \cdot x_{i}+b^{*}\right)-1=0=>y_{i}\left(w^{*} \cdot x_{i}+b^{*}\right)-y_j^2=0=>w^{*} \cdot x_{i}+b^{*}-y_j=0=>b^{*}=y_{j}-\sum_{i=1}^{N} y_{i} \alpha_{i}^{*}\left(x_{i} \cdot x_{j}\right) yi(w∗⋅xi+b∗)−1=0=>yi(w∗⋅xi+b∗)−yj2=0=>w∗⋅xi+b∗−yj=0=>b∗=yj−∑i=1Nyiαi∗(xi⋅xj)
由此定理可知, 分离超平面可以写成∑ i = 1 N α i ∗ y i ( x ⋅ x i ) + b ∗ = 0 \sum_{i=1}^{N} \alpha_{i}^{*} y_{i}\left(x \cdot x_{i}\right)+b^{*}=0 i=1∑Nαi∗yi(x⋅xi)+b∗=0
分类决策函数可以写成
f ( x ) = sign ( ∑ i = 1 N α i ∗ y i ( x ⋅ x i ) + b ∗ ) f(x)=\operatorname{sign}\left(\sum_{i=1}^{N} \alpha_{i}^{*} y_{i}\left(x \cdot x_{i}\right)+b^{*}\right) f(x)=sign(i=1∑Nαi∗yi(x⋅xi)+b∗)
线性支持向量机学习算法
输入: 训练数据集
T
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
⋯
,
(
x
N
,
y
N
)
}
T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{N}, y_{N}\right)\right\}
T={(x1,y1),(x2,y2),⋯,(xN,yN)}, 其中,
x
i
∈
X
=
R
n
x_{i} \in \mathcal{X}=\mathbf{R}^{n}
xi∈X=Rn,
y
i
∈
Y
=
{
−
1
,
+
1
}
,
i
=
1
,
2
,
⋯
,
N
;
y_{i} \in \mathcal{Y}=\{-1,+1\}, i=1,2, \cdots, N ;
yi∈Y={−1,+1},i=1,2,⋯,N;
输出:分离超平面和分类决策函数。
1、选择昰罚参数 C > 0 C>0 C>0, 构造并求解凸二次规划问题
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i s.t. ∑ i = 1 N α i y i = 0 0 ⩽ α i ⩽ C , i = 1 , 2 , ⋯ , N \begin{array}{ll} \min _{\alpha} & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} \\ \text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\ & 0 \leqslant \alpha_{i} \leqslant C, \quad i=1,2, \cdots, N \end{array} minα s.t. 21∑i=1N∑j=1Nαiαjyiyj(xi⋅xj)−∑i=1Nαi∑i=1Nαiyi=00⩽αi⩽C,i=1,2,⋯,N
求得最优解
α
∗
=
(
α
1
∗
,
α
2
∗
,
⋯
,
α
N
∗
)
T
\alpha^{*}=\left(\alpha_{1}^{*}, \alpha_{2}^{*}, \cdots, \alpha_{N}^{*}\right)^{\mathrm{T}}
α∗=(α1∗,α2∗,⋯,αN∗)T 。
2、计算.
w
∗
=
∑
i
=
1
N
α
i
∗
y
i
x
i
w^{*}=\sum_{i=1}^{N} \alpha_{i}^{*} y_{i} x_{i}
w∗=∑i=1Nαi∗yixi
选择
α
∗
\alpha^{*}
α∗ 的一个分量
α
j
∗
\alpha_{j}^{*}
αj∗ 适合条件
0
<
α
j
∗
<
C
0<\alpha_{j}^{*}<C
0<αj∗<C, 计算
b ∗ = y j − ∑ i = 1 N y i α i ∗ ( x i ⋅ x j ) b^{*}=y_{j}-\sum_{i=1}^{N} y_{i} \alpha_{i}^{*}\left(x_{i} \cdot x_{j}\right) b∗=yj−i=1∑Nyiαi∗(xi⋅xj)
3、求得分离超平面
w ∗ ⋅ x + b ∗ = 0 w^{*} \cdot x+b^{*}=0 w∗⋅x+b∗=0
分类决策函数:
f ( x ) = sign ( w ∗ ⋅ x + b ∗ ) f(x)=\operatorname{sign}\left(w^{*} \cdot x+b^{*}\right) f(x)=sign(w∗⋅x+b∗)
7.2.3 支持向量
在线性不可分的情况下, 将对偶问题
min
α
1
2
∑
i
=
1
N
∑
j
=
1
N
α
i
α
j
y
i
y
j
(
x
i
⋅
x
j
)
−
∑
i
=
1
N
α
i
s.t.
∑
i
=
1
N
α
i
y
i
=
0
0
⩽
α
i
⩽
C
,
i
=
1
,
2
,
⋯
,
N
\begin{array}{ll}\min _{\alpha} & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} \\\text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\& 0 \leqslant \alpha_{i} \leqslant C, \quad i=1,2, \cdots, N\end{array}
minα s.t. 21∑i=1N∑j=1Nαiαjyiyj(xi⋅xj)−∑i=1Nαi∑i=1Nαiyi=00⩽αi⩽C,i=1,2,⋯,N 的解
α
∗
=
(
α
1
∗
,
α
2
∗
,
⋯
,
α
N
∗
)
T
\alpha^{*}=\left(\alpha_{1}^{*}, \alpha_{2}^{*}, \cdots, \alpha_{N}^{*}\right)^{\mathrm{T}}
α∗=(α1∗,α2∗,⋯,αN∗)T中对应于
α
i
∗
>
0
\alpha_{i}^{*}>0
αi∗>0 的样本点
(
x
i
,
y
i
)
\left(x_{i}, y_{i}\right)
(xi,yi) 的实例
x
i
x_{i}
xi 称为支持向量 (软间隔的支持向量)。
如下图所示, 这时的支持向量要比线性可分时的情况复杂一些。图中, 分离超平面由实线表示, 间隔边界由虛线表示, 正例点由“o"表示, 负例点由 “
×
"
\times "
×" 表示。图中还标 出了实例
x
i
x_{i}
xi 到间隔边界的距离
ξ
i
∥
w
∥
\frac{\xi_{i}}{\|w\|}
∥w∥ξi 。

软间隔的支持向量 x i x_{i} xi 或者在间隔边界上, 或者在间隔边界与分离超平面之间, 或者在分离超平面误分一侧。
- 若 α i ∗ < C \alpha_{i}^{*}<C αi∗<C, 则 ξ i = 0 \xi_{i}=0 ξi=0, 支持向量 x i x_{i} xi 恰好落在间隔边界上;
- 若 α i ∗ = C , 0 < ξ i < 1 \alpha_{i}^{*}=C, 0<\xi_{i}<1 αi∗=C,0<ξi<1, 则分类正确, x i x_{i} xi 在间隔边界与分离超平面之间;
- 若 α i ∗ = C , ξ i = 1 \alpha_{i}^{*}=C, \xi_{i}=1 αi∗=C,ξi=1, 则 x i x_{i} xi 在分离超平面上;
- 若 α i ∗ = C , ξ i > 1 \alpha_{i}^{*}=C, \xi_{i}>1 αi∗=C,ξi>1, 则 x i x_{i} xi 位于分离超平面误 分一侧。
1的推导,已知: α i ∗ ( y i ( w ∗ ⋅ x i + b ∗ ) − 1 + ξ i ∗ ) = 0 μ i ∗ ξ i ∗ = 0 \alpha_{i}^{*}\left(y_{i}\left(w^{*} \cdot x_{i}+b^{*}\right)-1+\xi_{i}^{*}\right)=0 \\\mu_{i}^{*} \xi_{i}^{*}=0 αi∗(yi(w∗⋅xi+b∗)−1+ξi∗)=0μi∗ξi∗=0, C − α ∗ − μ ∗ = 0 C-\alpha^{*}-\mu^{*}=0 C−α∗−μ∗=0, α i ∗ < C \alpha_{i}^{*}<C αi∗<C; C − α ∗ = μ ∗ , ∵ α i ∗ < C , ∴ μ ∗ ≠ 0 , ∴ ξ i ∗ = 0 , ∴ y i ( w ∗ ⋅ x i + b ∗ ) − 1 = 0 C-\alpha^{*}=\mu^{*},∵\alpha_{i}^{*}<C,∴\mu^{*}\ne 0,∴\xi_{i}^{*}=0,∴y_{i}\left(w^{*} \cdot x_{i}+b^{*}\right)-1=0 C−α∗=μ∗,∵αi∗<C,∴μ∗=0,∴ξi∗=0,∴yi(w∗⋅xi+b∗)−1=0
2、3、4同理
7.2.4 合页损失函数
线性支持向量机学习的另一种解释, 就是最小化以下目标函数:
∑ i = 1 N [ 1 − y i ( w ⋅ x i + b ) ] + + λ ∥ w ∥ 2 \sum_{i=1}^{N}\left[1-y_{i}\left(w \cdot x_{i}+b\right)\right]_{+}+\lambda\|w\|^{2} i=1∑N[1−yi(w⋅xi+b)]++λ∥w∥2
目标函数的第 1 项是经验损失或经验风险, 函数
L ( y ( w ⋅ x + b ) ) = [ 1 − y ( w ⋅ x + b ) ] + L(y(w \cdot x+b))=[1-y(w \cdot x+b)]_{+} L(y(w⋅x+b))=[1−y(w⋅x+b)]+
称为合页损失函数(hinge loss function)。下标 “ + " +" +" 表示以下取正值的函数。
[ z ] + = { z , z > 0 0 , z ⩽ 0 [z]_{+}= \begin{cases}z, & z>0 \\ 0, & z \leqslant 0\end{cases} [z]+={z,0,z>0z⩽0
- 当样本点 ( x i , y i ) \left(x_{i}, y_{i}\right) (xi,yi) 被正确分类且函数间隔(确信度) y i ( w ⋅ x i + b ) y_{i}\left(w \cdot x_{i}+b\right) yi(w⋅xi+b) 大于 1 时,损失是 0 ,
- 否则损失是 1 − y i ( w ⋅ x i + b ) 1-y_{i}\left(w \cdot x_{i}+b\right) 1−yi(w⋅xi+b) 。
- 目标函数的第 2 项是系数为 λ \lambda λ 的 w w w 的 L 2 L_{2} L2 范数, 是正则化项。
合页损失函数图像

7.3 非线性支持向量机与核函数
7.3.1 核技巧
-
非线性分类问题

用线性分类方法求解非线性分类问题分为两步:
- 首先使用一个变换将原空间的数据映射到新空间;
- 在新空间里用线性分类学习方法从训练数据中学习分类模型。
核技巧应用到支持向量机,其基本想法就是通过一个非线性变换将输入空间 (欧氏空间 R n \mathbf{R}^{n} Rn 或离散集合) 对应于一个特征空间 (希尔伯特空间 H \mathcal{H} H ),使得在输入空间 R n \mathbf{R}^{n} Rn 中的超曲面模型对应于特征空间 H \mathcal{H} H 中的超平面模型 (支持向量机)。这样, 分类问题的学习任务通过在特征空间中求解线性支持向量机就可以完成。
-
核函数的定义
核函数 设 X \mathcal{X} X 是输入空间 (欧氏空间 R n \mathbf{R}^{n} Rn 的子集或离散集合 ), 又设 H \mathcal{H} H 为特征空间 ( 希尔伯特空间 ), 如果存在一个从 X \mathcal{X} X 到 H \mathcal{H} H 的映射
ϕ ( x ) : X → H \phi(x): \mathcal{X} \rightarrow \mathcal{H} ϕ(x):X→H使得对所有 x , z ∈ X x, z \in \mathcal{X} x,z∈X, 函数 K ( x , z ) K(x, z) K(x,z) 满足条件
K ( x , z ) = ϕ ( x ) ∙ ϕ ( z ) K(x, z)=\phi(x) \bullet \phi(z) K(x,z)=ϕ(x)∙ϕ(z)则称 K ( x , z ) K(x, z) K(x,z) 为核函数, ϕ ( x ) \phi(x) ϕ(x) 为映射函数, 式中 ϕ ( x ) ⋅ ϕ ( z ) \phi(x) \cdot \phi(z) ϕ(x)⋅ϕ(z) 为 ϕ ( x ) \phi(x) ϕ(x) 和 ϕ ( z ) \phi(z) ϕ(z) 的内积。 核技巧的想法是, 在学习与预测中只定义核函数 K ( x , z ) K(x, z) K(x,z), 而不显式地定义映射函数 ϕ \phi ϕ 。因为, 直接计算 K ( x , z ) K(x, z) K(x,z) 比较容易, 而通过 ϕ ( x ) \phi(x) ϕ(x) 和 ϕ ( z ) \phi(z) ϕ(z) 计算 K ( x , z ) K(x, z) K(x,z) 并不容易。
注意, ϕ \phi ϕ 是输入空间 R n \mathbf{R}^{n} Rn 到特征空间 H \mathcal{H} H 的映射, 特征空间 H \mathcal{H} H 一般是高维的, 甚至是无穷维的。可以看到, 对于给定的核 K ( x , z ) K(x, z) K(x,z), 特征空间 H \mathcal{H} H 和映射函数 ϕ \phi ϕ 的取法并不唯 一, 可以取不同的特征空间, 即便是在同一特征空间里也可以取不同的映射。
-
核技巧在支持向量机中的应用
在对偶问题的目标函数 min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ∙ x j ) − ∑ i = 1 N α i \min _{\alpha} \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \bullet x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} minα21∑i=1N∑j=1Nαiαjyiyj(xi∙xj)−∑i=1Nαi 中的内积 x i ∙ x j x_{i} \bullet x_{j} xi∙xj 可以用核函数 K ( x i , x j ) = ϕ ( x i ) ∙ ϕ ( x j ) K\left(x_{i}, x_{j}\right)=\phi\left(x_{i}\right) \bullet \phi\left(x_{j}\right) K(xi,xj)=ϕ(xi)∙ϕ(xj) 来代替。此时对偶问题的目标函数成为
W ( α ) = 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j K ( x i , x j ) − ∑ i = 1 N α i W(\alpha)=\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j} K\left(x_{i}, x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} W(α)=21i=1∑Nj=1∑NαiαjyiyjK(xi,xj)−i=1∑Nαi同样, 分类决策函数中的内积也可以用核函数代替, 而分类决策函数式成为
f ( x ) = sign ( ∑ i = 1 N s a i ∗ y i ϕ ( x i ) ∙ ϕ ( x ) + b ∗ ) = sign ( ∑ i = 1 N s a i ∗ y i K ( x i , x ) + b ∗ ) \begin{aligned} f(x) &=\operatorname{sign}\left(\sum_{i=1}^{N_{s}} a_{i}^{*} y_{i} \phi\left(x_{i}\right) \bullet \phi(x)+b^{*}\right) \\ &=\operatorname{sign}\left(\sum_{i=1}^{N_{s}} a_{i}^{*} y_{i} K\left(x_{i}, x\right)+b^{*}\right) \end{aligned} f(x)=sign(i=1∑Nsai∗yiϕ(xi)∙ϕ(x)+b∗)=sign(i=1∑Nsai∗yiK(xi,x)+b∗)这等价于经过映射函数 ϕ \phi ϕ 将原来的输入空间变换到一个新的特征空间, 将输入空 间中的内积 x i ∙ x j x_{i} \bullet x_{j} xi∙xj 变换为特征空间中的内积 ϕ ( x i ) ∙ ϕ ( x j ) \phi\left(x_{i}\right) \bullet \phi\left(x_{j}\right) ϕ(xi)∙ϕ(xj), 在新的特征空间里从训 练样本中学习线性支持向量机。当映射函数是非线性函数时, 学习到的含有核函数的支持向量机是非线性分类模型。
- 在核函数 K ( x , z ) K(x, z) K(x,z) 给定的条件下, 可以利用解线性分类问题的方法求 解非线性分类问题的支持向量机。
- 学习是隐式地在特征空间进行的, 不需要显式地定 义特征空间和映射函数。这样的技巧称为核技巧, 它是巧妙地利用线性分类学习方法 与核函数解决非线性问题的技术。
- 在实际应用中, 往往依赖领域知识直接选择核函数, 核函数选择的有效性需要通过实验验证。
7.3.2正定核
知识补充-半正定矩阵
给定一个大小施 n × n n \times n n×n 的实对称矩阵 A A A, 若对于任意长度为 n n n 的向量 x \boldsymbol{x} x, 有 x T A x ≥ 0 \boldsymbol{x}^{T} A \boldsymbol{x} \geq 0 xTAx≥0 恒成立,则矩阵 A A A 是一个半正定矩阵。
推导正定核的充要条件。
通常所说的核函数就是正定核函数(positive definite kernel function)。
证明此定理的预备知识。
假设 K ( x , z ) K(x, z) K(x,z) 是定义在 X × X \mathcal{X} \times \mathcal{X} X×X 上的对称函数, 并且对任意的 x 1 , x 2 , ⋯ , x m ∈ x_{1}, x_{2}, \cdots, x_{m} \in x1,x2,⋯,xm∈ X , K ( x , z ) \mathcal{X}, K(x, z) X,K(x,z) 关于 x 1 , x 2 , ⋯ , x m x_{1}, x_{2}, \cdots, x_{m} x1,x2,⋯,xm 的 Gram 矩阵是半正定的。可以依据函数 K ( x , z ) K(x, z) K(x,z), 构成一个希尔伯特空间(Hilbert space), 其步骤是:首先定义映射 ϕ \phi ϕ 并构成向量空间 S \mathcal{S} S; 然后在 S \mathcal{S} S 上定义内积构成内积空间; 最后将 S \mathcal{S} S 完备化构成希尔伯特空间。
-
定义映射, 构成向量空间 S \mathcal{S} S
先定义映射
ϕ : x → K ( ∙ , x ) \phi: x \rightarrow K(\bullet, x) ϕ:x→K(∙,x)根据这一映射, 对任意 x i ∈ X , α i ∈ R , i = 1 , 2 , ⋯ , m x_{i} \in \mathcal{X}, \alpha_{i} \in \mathbf{R}, i=1,2, \cdots, m xi∈X,αi∈R,i=1,2,⋯,m, 定义线性组合
f ( ⋅ ) = ∑ i = 1 m α i K ( ∙ , x i ) f(\cdot)=\sum_{i=1}^{m} \alpha_{i} K\left(\bullet, x_{i}\right) f(⋅)=i=1∑mαiK(∙,xi)考虑由线性组合为元素的集合 S \mathcal{S} S 。由于集合 S \mathcal{S} S 对加法和数乘运算是封闭的, 所以 S \mathcal{S} S 构成一个向量空间.
-
在 S \mathcal{S} S 上定义内积, 使其成为内积空间
内积空间就是定义了内积的线性空间。
在 S \mathcal{S} S 上定义一个运算 ∗ * ∗ : 对任意 f , g ∈ S f, g \in \mathcal{S} f,g∈S,
f ( ∙ ) = ∑ i = 1 m α i K ( ∙ , x i ) g ( ∙ ) = ∑ j = 1 l β j K ( ∙ , z j ) \begin{aligned} &f(\bullet)=\sum_{i=1}^{m} \alpha_{i} K\left(\bullet, x_{i}\right) \\ &g(\bullet)=\sum_{j=1}^{l} \beta_{j} K\left(\bullet, z_{j}\right) \end{aligned} f(∙)=i=1∑mαiK(∙,xi)g(∙)=j=1∑lβjK(∙,zj)定义运算 ∗ * ∗
f ∗ g = ∑ i = 1 m ∑ j = 1 l α i β j K ( x i , z j ) f * g=\sum_{i=1}^{m} \sum_{j=1}^{l} \alpha_{i} \beta_{j} K\left(x_{i}, z_{j}\right) f∗g=i=1∑mj=1∑lαiβjK(xi,zj)证明运算 ∗ * ∗ 是空间 S \mathcal{S} S 的内积。为此要证:
(1) ( c f ) ∗ g = c ( f ∗ g ) , c ∈ R (c f) * g=c(f * g), c \in \mathbf{R} (cf)∗g=c(f∗g),c∈R
(2) ( f + g ) ∗ h = f ∗ h + g ∗ h , h ∈ S (f+g) * h=f * h+g * h, h \in \mathcal{S} (f+g)∗h=f∗h+g∗h,h∈S
(3) f ∗ g = g ∗ f f * g=g * f f∗g=g∗f
(4) f ∗ f ⩾ 0 f * f \geqslant 0 f∗f⩾0,
f ∗ f = 0 ⇔ f = 0 f * f=0 \Leftrightarrow f=0 f∗f=0⇔f=0其中, ( 1 ) ∼ ( 3 ) (1) \sim(3) (1)∼(3) 由式 f ( ∙ ) = ∑ i = 1 m α i K ( ∙ , x i ) f(\bullet)=\sum_{i=1}^{m} \alpha_{i} K\left(\bullet, x_{i}\right) f(∙)=∑i=1mαiK(∙,xi) 式 g ( ∙ ) = ∑ j = 1 l β j K ( ∙ , z j ) g(\bullet)=\sum_{j=1}^{l} \beta_{j} K\left(\bullet, z_{j}\right) g(∙)=∑j=1lβjK(∙,zj) 及 K ( x , z ) K(x, z) K(x,z) 的对称性容易得到(很显然)。
K ( x , z ) K(x, z) K(x,z)的对称性证明, K ( x , z ) = ϕ ( x ) ∙ ϕ ( z ) , K ( z , x ) = ϕ ( z ) ∙ ϕ ( x ) , K ( x , z ) = K ( z , x ) K(x, z)=\phi(x) \bullet \phi(z),K(z, x)=\phi(z) \bullet \phi(x),K(x, z)=K(z, x) K(x,z)=ϕ(x)∙ϕ(z),K(z,x)=ϕ(z)∙ϕ(x),K(x,z)=K(z,x)
现证 ( 4 ) (4) (4) 之 式 f ∗ f ⩾ 0 f * f \geqslant 0 f∗f⩾0 。 由式 f ( ∙ ) = ∑ i = 1 m α i K ( ∙ , x i ) f(\bullet)=\sum_{i=1}^{m} \alpha_{i} K\left(\bullet, x_{i}\right) f(∙)=∑i=1mαiK(∙,xi) 及式 f ∗ g = ∑ i = 1 m ∑ j = 1 l α i β j K ( x i , z j ) f * g=\sum_{i=1}^{m} \sum_{j=1}^{l} \alpha_{i} \beta_{j} K\left(x_{i}, z_{j}\right) f∗g=∑i=1m∑j=1lαiβjK(xi,zj) 可得:
f ∗ f = ∑ i , j = 1 m α i α j K ( x i , x j ) f * f=\sum_{i, j=1}^{m} \alpha_{i} \alpha_{j} K\left(x_{i}, x_{j}\right) f∗f=i,j=1∑mαiαjK(xi,xj)由 Gram 矩阵的半正定性知上式右端非负, 即 f ∗ f ⩾ 0 f * f \geqslant 0 f∗f⩾0 。
再证 (4) 之式 f ∗ f = 0 ⇔ f = 0 f * f=0 \Leftrightarrow f=0 f∗f=0⇔f=0 。 充分性显然。为证必要性(左推右), 首先证明不等式:
∣ f ∗ g ∣ 2 ⩽ ( f ∗ f ) ( g ∗ g ) |f * g|^{2} \leqslant(f * f)(g * g) ∣f∗g∣2⩽(f∗f)(g∗g)设 f , g ∈ S , λ ∈ R f, g \in \mathcal{S}, \lambda \in \mathbf{R} f,g∈S,λ∈R, 则 f + λ g ∈ S f+\lambda g \in \mathcal{S} f+λg∈S, 于是,
( f + λ g ) ∗ ( f + λ g ) ⩾ 0 f ∗ f + 2 λ ( f ∗ g ) + λ 2 ( g ∗ g ) ⩾ 0 \begin{gathered} (f+\lambda g) *(f+\lambda g) \geqslant 0 \\ f * f+2 \lambda(f * g)+\lambda^{2}(g * g) \geqslant 0 \end{gathered} (f+λg)∗(f+λg)⩾0f∗f+2λ(f∗g)+λ2(g∗g)⩾0其左端是 λ \lambda λ 的二次三项式, 非负, 其判别式小于等于 0 , 即
( f ∗ g ) 2 − ( f ∗ f ) ( g ∗ g ) ⩽ 0 (f * g)^{2}-(f * f)(g * g) \leqslant 0 (f∗g)2−(f∗f)(g∗g)⩽0于是式 ∣ f ∗ g ∣ 2 ⩽ ( f ∗ f ) ( g ∗ g ) |f * g|^{2} \leqslant(f * f)(g * g) ∣f∗g∣2⩽(f∗f)(g∗g) 得证。
现证若 f ∗ f = 0 f * f=0 f∗f=0, 则 f = 0 f=0 f=0 。事实上, 若
f ( ∙ ) = ∑ i = 1 m α i K ( ∙ , x i ) f(\bullet)=\sum_{i=1}^{m} \alpha_{i} K\left(\bullet, x_{i}\right) f(∙)=i=1∑mαiK(∙,xi)则按运算 ∗ * ∗ 的定义式 f ∗ g = ∑ i = 1 m ∑ j = 1 l α i β j K ( x i , z j ) f * g=\sum_{i=1}^{m} \sum_{j=1}^{l} \alpha_{i} \beta_{j} K\left(x_{i}, z_{j}\right) f∗g=∑i=1m∑j=1lαiβjK(xi,zj), 对任意的 x ∈ X x \in \mathcal{X} x∈X, 有
K ( ∙ , x ) ∗ f = ∑ i = 1 m α i K ( x , x i ) = f ( x ) K(\bullet, x) * f=\sum_{i=1}^{m} \alpha_{i} K\left(x, x_{i}\right)=f(x) K(∙,x)∗f=i=1∑mαiK(x,xi)=f(x)于是,
∣ f ( x ) ∣ 2 = ∣ K ( ∙ , x ) ∗ f ∣ 2 |f(x)|^{2}=|K(\bullet, x) * f|^{2} ∣f(x)∣2=∣K(∙,x)∗f∣2由式 ∣ f ∗ g ∣ 2 ⩽ ( f ∗ f ) ( g ∗ g ) |f * g|^{2} \leqslant(f * f)(g * g) ∣f∗g∣2⩽(f∗f)(g∗g) 和式 f ∗ f ⩾ 0 f * f \geqslant 0 f∗f⩾0 有
∣ K ( ∙ , x ) ∗ f ∣ 2 ⩽ ( K ( ∙ , x ) ∗ K ( ∙ , x ) ) ( f ∗ f ) = K ( x , x ) ( f ∗ f ) \begin{aligned} |K(\bullet, x) * f|^{2} & \leqslant(K(\bullet, x) * K(\bullet, x))(f * f) \\ &=K(x, x)(f * f) \end{aligned} ∣K(∙,x)∗f∣2⩽(K(∙,x)∗K(∙,x))(f∗f)=K(x,x)(f∗f)由式 ∣ f ( x ) ∣ 2 = ∣ K ( ∙ , x ) ∗ f ∣ 2 |f(x)|^{2}=|K(\bullet, x) * f|^{2} ∣f(x)∣2=∣K(∙,x)∗f∣2 有
∣ f ( x ) ∣ 2 ⩽ K ( x , x ) ( f ∗ f ) |f(x)|^{2} \leqslant K(x, x)(f * f) ∣f(x)∣2⩽K(x,x)(f∗f)此式表明, 当 f ∗ f = 0 f * f=0 f∗f=0 时, 对任意的 x x x 都有 ∣ f ( x ) ∣ = 0 |f(x)|=0 ∣f(x)∣=0 。
至此, 证明了 ∗ * ∗ 为向量空间 S \mathcal{S} S 的内积。赋予内积的向量空间为内积空间。因此 S \mathcal{S} S 是一个内积空间。既然 ∗ * ∗ 为 S \mathcal{S} S 的内积运算, 那么仍然用 ∙ \bullet ∙ 表示, 即若
f ( ∙ ) = ∑ i = 1 m α i K ( ∙ , x i ) , g ( ∙ ) = ∑ i = 1 l β j K ( ∙ , z j ) f(\bullet)=\sum_{i=1}^{m} \alpha_{i} K\left(\bullet, x_{i}\right), \quad g(\bullet)=\sum_{i=1}^{l} \beta_{j} K\left(\bullet, z_{j}\right) f(∙)=i=1∑mαiK(∙,xi),g(∙)=i=1∑lβjK(∙,zj)则
f ∙ g = ∑ i = 1 m ∑ j = 1 l α i β j K ( x i , z j ) f \bullet g=\sum_{i=1}^{m} \sum_{j=1}^{l} \alpha_{i} \beta_{j} K\left(x_{i}, z_{j}\right) f∙g=i=1∑mj=1∑lαiβjK(xi,zj)-
将内积空间 S \mathcal{S} S 完备化为希尔伯特空间
现在将内积空间 S \mathcal{S} S 完备化。由式 f ∙ g = ∑ i = 1 m ∑ j = 1 l α i β j K ( x i , z j ) f \bullet g=\sum_{i=1}^{m} \sum_{j=1}^{l} \alpha_{i} \beta_{j} K\left(x_{i}, z_{j}\right) f∙g=∑i=1m∑j=1lαiβjK(xi,zj) 定义的内积可以得到范数
∥ f ∥ = f ∙ f \|f\|=\sqrt{f \bullet f} ∥f∥=f∙f因此, S \mathcal{S} S 是一个赋范向量空间。根据泛函分析理论, 对于不完备的赋范向量空间 S , − \mathcal{S},- S,− 定可以使之完备化, 得到完备的赋范向量空间 H \mathcal{H} H 。一个内积空间, 当作为一个赋范向量空间是完备的时候, 就是希尔伯特空间。这样, 就得到了希尔伯特空间 H \mathcal{H} H 。
这一希尔伯特空间 H \mathcal{H} H 称为再生核希尔伯特空间(reproducing kernel Hilbert space, RKHS)。这是由于核 K K K 具有再生性, 即满足
K ( ∙ , x ) ∙ f = f ( x ) K(\bullet, x) \bullet f=f(x) K(∙,x)∙f=f(x)及
K ( ∙ , x ) ∙ K ( ∙ , z ) = K ( x , z ) K(\bullet, x) \bullet K(\bullet, z)=K(x, z) K(∙,x)∙K(∙,z)=K(x,z)称为再生核。
-
正定核的充要条件
正定核的充要条件 设 K : X × X → R K: \mathcal{X} \times \mathcal{X} \rightarrow \mathbf{R} K:X×X→R 是对称函数, 则 K ( x , z ) K(x, z) K(x,z) 为正 定核函数的充要条件是对任意 x i ∈ X , i = 1 , 2 , ⋯ , m , K ( x , z ) x_{i} \in \mathcal{X}, i=1,2, \cdots, m, K(x, z) xi∈X,i=1,2,⋯,m,K(x,z) 对应的 Gram 矩阵:
K = [ K ( x i , x j ) ] m × m K=\left[K\left(x_{i}, x_{j}\right)\right]_{m \times m} K=[K(xi,xj)]m×m是半正定矩阵。
证明 必要性。由于 K ( x , z ) K(x, z) K(x,z) 是 X × X \mathcal{X} \times \mathcal{X} X×X 上的正定核, 所以存在从 X \mathcal{X} X 到希尔伯特空间 H \mathcal{H} H 的映射 ϕ \phi ϕ, 使得
K ( x , z ) = ϕ ( x ) ∙ ϕ ( z ) K(x, z)=\phi(x) \bullet\phi(z) K(x,z)=ϕ(x)∙ϕ(z)
于是, 对任意 x 1 , x 2 , ⋯ , x m x_{1}, x_{2}, \cdots, x_{m} x1,x2,⋯,xm, 构造 K ( x , z ) K(x, z) K(x,z) 关于 x 1 , x 2 , ⋯ , x m x_{1}, x_{2}, \cdots, x_{m} x1,x2,⋯,xm 的 Gram 矩阵
[ K i j ] m × m = [ K ( x i , x j ) ] m × m \left[K_{i j}\right]_{m \times m}=\left[K\left(x_{i}, x_{j}\right)\right]_{m \times m} [Kij]m×m=[K(xi,xj)]m×m
对任意 c 1 , c 2 , ⋯ , c m ∈ R c_{1}, c_{2}, \cdots, c_{m} \in \mathbf{R} c1,c2,⋯,cm∈R, 有
∑ i , j = 1 m c i c j K ( x i , x j ) = ∑ i , j = 1 m c i c j ( ϕ ( x i ) ∙ ϕ ( x j ) ) = ( ∑ i c i ϕ ( x i ) ) ∙ ( ∑ j c j ϕ ( x j ) ) = ∥ ∑ i c i ϕ ( x i ) ∥ 2 ⩾ 0 \begin{aligned} \sum_{i, j=1}^{m} c_{i} c_{j} K\left(x_{i}, x_{j}\right) &=\sum_{i, j=1}^{m} c_{i} c_{j}\left(\phi\left(x_{i}\right) \bullet\phi\left(x_{j}\right)\right) \\ &=\left(\sum_{i} c_{i} \phi\left(x_{i}\right)\right) \bullet\left(\sum_{j} c_{j} \phi\left(x_{j}\right)\right) \\ &=\left\|\sum_{i} c_{i} \phi\left(x_{i}\right)\right\|^{2} \geqslant 0 \end{aligned} i,j=1∑mcicjK(xi,xj)=i,j=1∑mcicj(ϕ(xi)∙ϕ(xj))=(i∑ciϕ(xi))∙(j∑cjϕ(xj))=∥∥∥∥∥i∑ciϕ(xi)∥∥∥∥∥2⩾0
表明 K ( x , z ) K(x, z) K(x,z) 关于 x 1 , x 2 , ⋯ , x m x_{1}, x_{2}, \cdots, x_{m} x1,x2,⋯,xm 的 Gram 矩阵是半正定的。
充分性。已知对称函数 K ( x , z ) K(x, z) K(x,z) 对任意 x 1 , x 2 , ⋯ , x m ∈ X , K ( x , z ) x_{1}, x_{2}, \cdots, x_{m} \in \mathcal{X}, K(x, z) x1,x2,⋯,xm∈X,K(x,z) 关于 x 1 , x 2 , ⋯ , x m x_{1}, x_{2}, \cdots, x_{m} x1,x2,⋯,xm 的 Gram 矩阵是半正定的。根据前面的结果, 对给定的 K ( x , z ) K(x, z) K(x,z), 可以 构造从 X \mathcal{X} X 到某个希尔伯特空间 H \mathcal{H} H 的映射:ϕ : x → K ( ∙ , x ) \phi: x \rightarrow K(\bullet, x) ϕ:x→K(∙,x)
而且
K ( ∙ , x ) ∙ f = f ( x ) K(\bullet, x) \bullet f=f(x) K(∙,x)∙f=f(x)
并且
K ( ∙ , x ) ∙ K ( ∙ , z ) = K ( x , z ) K(\bullet, x) \bullet K(\bullet, z)=K(x, z) K(∙,x)∙K(∙,z)=K(x,z)
由式 ϕ : x → K ( ∙ , x ) \phi: x \rightarrow K(\bullet, x) ϕ:x→K(∙,x) 即得
K ( x , z ) = ϕ ( x ) ∙ ϕ ( z ) K(x, z)=\phi(x) \bullet\phi(z) K(x,z)=ϕ(x)∙ϕ(z)
表明 K ( x , z ) K(x, z) K(x,z) 是 X × X \mathcal{X} \times \mathcal{X} X×X 上的核函数。
核函数另一定义:正定核的充要条件。
正定核的等价定义 设 X ⊂ R n , K ( x , z ) \mathcal{X} \subset \mathbf{R}^{n}, K(x, z) X⊂Rn,K(x,z) 是定义在 X × X \mathcal{X} \times \mathcal{X} X×X 上的对称 函数, 如果对任意 x i ∈ X , i = 1 , 2 , ⋯ , m , K ( x , z ) x_{i} \in \mathcal{X}, i=1,2, \cdots, m, K(x, z) xi∈X,i=1,2,⋯,m,K(x,z) 对应的 Gram 矩阵
K = [ K ( x i , x j ) ] m × m K=\left[K\left(x_{i}, x_{j}\right)\right]_{m \times m} K=[K(xi,xj)]m×m是半正定矩阵, 则称 K ( x , z ) K(x, z) K(x,z) 是正定核。
这一定义在构造核函数时很有用。但对于一个具体函数 K ( x , z ) K(x, z) K(x,z) 来说, 检验它是否为正定核函数并不容易, 因为要求对任意有限输入集 { x 1 , x 2 , ⋯ , x m } \left\{x_{1}, x_{2}, \cdots, x_{m}\right\} {x1,x2,⋯,xm} 验证 K K K 对 应的 Gram 矩阵是否为半正定的。在实际问题中往往应用已有的核函数。另外, 由 Mercer 定理可以得到 Mercer 核 (Mercer kernel), 正定核比 Mercer 核更具一般性.
-
7.3.3 常用核函数
-
多项式核函数 (polynomial kernel function)
K ( x , z ) = ( x ∙ z + 1 ) p K(x, z)=(x \bullet z+1)^{p} K(x,z)=(x∙z+1)p对应的支持向量机是一个 p p p 次多项式分类器。在此情形下, 分类决策函数成为
f ( x ) = sign ( ∑ i = 1 N s a i ∗ y i ( x i ∙ x + 1 ) p + b ∗ ) f(x)=\operatorname{sign}\left(\sum_{i=1}^{N_{s}} a_{i}^{*} y_{i}\left(x_{i} \bullet x+1\right)^{p}+b^{*}\right) f(x)=sign(i=1∑Nsai∗yi(xi∙x+1)p+b∗) -
高斯核函数 (Gaussian kernel function)
K ( x , z ) = exp ( − ∥ x − z ∥ 2 2 σ 2 ) K(x, z)=\exp \left(-\frac{\|x-z\|^{2}}{2 \sigma^{2}}\right) K(x,z)=exp(−2σ2∥x−z∥2)对应的支持向量机是高斯径向基函数 (radial basis function) 分类器。在此情形下, 分 类决策函数成为
f ( x ) = sign ( ∑ i = 1 N s a i ∗ y i exp ( − ∥ x − x i ∥ 2 2 σ 2 ) + b ∗ ) f(x)=\operatorname{sign}\left(\sum_{i=1}^{N_{s}} a_{i}^{*} y_{i} \exp \left(-\frac{\left\|x-x_{i}\right\|^{2}}{2 \sigma^{2}}\right)+b^{*}\right) f(x)=sign(i=1∑Nsai∗yiexp(−2σ2∥x−xi∥2)+b∗) -
字符串核函数 (string kernel function)
两个字符串 s s s 和 t t t 上的字符串核函数是基于映射 ϕ n \phi_{n} ϕn 的特征空间中的内积:
k n ( s , t ) = ∑ u ∈ Σ n [ ϕ n ( s ) ] u [ ϕ n ( t ) ] u = ∑ u ∈ Σ n ∑ ( i , j ) : s ( i ) = t ( j ) = u λ l ( i ) λ l ( j ) \begin{aligned} k_{n}(s, t) &=\sum_{u \in \Sigma^{n}}\left[\phi_{n}(s)\right]_{u}\left[\phi_{n}(t)\right]_{u} \\ &=\sum_{u \in \Sigma^{n}} \sum_{(i, j): s(i)=t(j)=u} \lambda^{l(i)} \lambda^{l(j)} \end{aligned} kn(s,t)=u∈Σn∑[ϕn(s)]u[ϕn(t)]u=u∈Σn∑(i,j):s(i)=t(j)=u∑λl(i)λl(j)字符串核函数 k n ( s , t ) k_{n}(s, t) kn(s,t) 给出了字符串 s s s 和 t t t 中长度等于 n n n 的所有子串组成的特征向量 的余弦相似度 (cosine similarity)。直观上, 两个字符串相同的子串越多, 它们就越相似, 字符串核函数的值就越大。字符串核函数可以由动态规划快速地计算。
7.3.4 非线性支持向量分类机
非线性支持向量机学习算法 输入: 训练数据集
T
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
⋯
,
(
x
N
,
y
N
)
}
T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{N}, y_{N}\right)\right\}
T={(x1,y1),(x2,y2),⋯,(xN,yN)}, 其中
x
i
∈
X
=
R
n
,
y
i
∈
x_{i} \in \mathcal{X}=\mathbf{R}^{n}, y_{i} \in
xi∈X=Rn,yi∈
Y
=
{
−
1
,
+
1
}
,
i
=
1
,
2
,
⋯
,
N
\mathcal{Y}=\{-1,+1\}, i=1,2, \cdots, N
Y={−1,+1},i=1,2,⋯,N
输出: 分类决策函数。
-
选取适当的核函数 K ( x , z ) K(x, z) K(x,z) 和适当的参数 C C C, 构造并求解最优化问题
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j K ( x i , x j ) − ∑ i = 1 N α i s.t. ∑ i = 1 N α i y i = 0 0 ⩽ α i ⩽ C , i = 1 , 2 , ⋯ , N \begin{array}{ll} \min _{\alpha} & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j} K\left(x_{i}, x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} \\ \text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\ & 0 \leqslant \alpha_{i} \leqslant C, \quad i=1,2, \cdots, N \end{array} minα s.t. 21∑i=1N∑j=1NαiαjyiyjK(xi,xj)−∑i=1Nαi∑i=1Nαiyi=00⩽αi⩽C,i=1,2,⋯,N求得最优解 α ∗ = ( α 1 ∗ , α 2 ∗ , ⋯ , α N ∗ ) T \alpha^{*}=\left(\alpha_{1}^{*}, \alpha_{2}^{*}, \cdots, \alpha_{N}^{*}\right)^{\mathrm{T}} α∗=(α1∗,α2∗,⋯,αN∗)T 。
-
选择 α ∗ \alpha^{*} α∗ 的一个正分量 0 < α j ∗ < C 0<\alpha_{j}^{*}<C 0<αj∗<C, 计算
b ∗ = y j − ∑ i = 1 N α i ∗ y i K ( x i , x j ) b^{*}=y_{j}-\sum_{i=1}^{N} \alpha_{i}^{*} y_{i} K\left(x_{i}, x_{j}\right) b∗=yj−i=1∑Nαi∗yiK(xi,xj) -
构造决策函数:
f ( x ) = sign ( ∑ i = 1 N α i ∗ y i K ( x , x i ) + b ∗ ) f(x)=\operatorname{sign}\left(\sum_{i=1}^{N} \alpha_{i}^{*} y_{i} K\left(x, x_{i}\right)+b^{*}\right) f(x)=sign(i=1∑Nαi∗yiK(x,xi)+b∗)当 K ( x , z ) K(x, z) K(x,z) 是正定核函数时, 问题 min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j K ( x i , x j ) − ∑ i = 1 N α i s.t. ∑ i = 1 N α i y i = 0 0 ⩽ α i ⩽ C , i = 1 , 2 , ⋯ , N \begin{array}{ll}\min _{\alpha} & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j} K\left(x_{i}, x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} \\\text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\& 0 \leqslant \alpha_{i} \leqslant C, \quad i=1,2, \cdots, N\end{array} minα s.t. 21∑i=1N∑j=1NαiαjyiyjK(xi,xj)−∑i=1Nαi∑i=1Nαiyi=00⩽αi⩽C,i=1,2,⋯,N 是凸二次规划问题, 解是存在的。
7.4 序列最小最优化算法
高效的实现支持向量机的学习—序列最小最优化(sequential minimal optimization, SMO )算法
SMO 算法要解如下凸二次规划的对偶问题:
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j K ( x i , x j ) − ∑ i = 1 N α i s.t. ∑ i = 1 N α i y i = 0 0 ⩽ α i ⩽ C , i = 1 , 2 , ⋯ , N \begin{array}{ll} \min _{\alpha} & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j} K\left(x_{i}, x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} \\ \text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\ & 0 \leqslant \alpha_{i} \leqslant C, \quad i=1,2, \cdots, N \end{array} minα s.t. 21∑i=1N∑j=1NαiαjyiyjK(xi,xj)−∑i=1Nαi∑i=1Nαiyi=00⩽αi⩽C,i=1,2,⋯,N
在这个问题中, 变量是拉格朗日乘子, 一个变量 α i \alpha_{i} αi 对应于一个样本点 ( x i , y i ) \left(x_{i}, y_{i}\right) (xi,yi); 变量的 总数等于训练样本容量 N N N 。
SMO 算法是一种启发式算法, 其基本思路是: 如果所有变量的解都满足此最优化问题的KKT条件 (Karush-Kuhn-Tucker conditions),那么这个最优化问题的解就得到了。因为 KKT 条件是该最优化问题的充分必要条件。否则, 选择两个变量, 固定其他变量, 针对这两个变量构建一个二次规划问题。这个二次规划问题关于这两个 变量的解应该更接近原始二次规划问题的解, 因为这会使得原始二次规划问题的目标 函数值变得更小。重要的是, 这时子问题可以通过解析方法求解, 这样就可以大大提高整个算法的计算速度。子问题有两个变量, 一个是违反 KKT 条件最严重的那一个, 另一个由约束条件自动确定。如此, SMO 算法将原问题不断分解为子问题并对子问 题求解, 进而达到求解原问题的目的。 注意, 子问题的两个变量中只有一个是自由变量。假设 α 1 , α 2 \alpha_{1}, \alpha_{2} α1,α2 为两个变量, α 3 , α 4 , ⋯ , α N \alpha_{3}, \alpha_{4}, \cdots, \alpha_{N} α3,α4,⋯,αN 固定, 那么由等式约束 ∑ i = 1 N α i y i = 0 \sum_{i=1}^{N} \alpha_{i} y_{i}=0 ∑i=1Nαiyi=0 可知
α 1 = − y 1 ∑ i = 2 N α i y i \alpha_{1}=-y_{1} \sum_{i=2}^{N} \alpha_{i} y_{i} α1=−y1i=2∑Nαiyi
推导过程 α 1 y 1 = − ∑ i = 2 N α i y i , α 1 y 1 y 1 = − y 1 ∑ i = 2 N α i y i , ∵ y 1 y 1 = 1 , ∴ α 1 = − y 1 ∑ i = 2 N α i y i \alpha_{1}y_1=- \sum_{i=2}^{N} \alpha_{i} y_{i},\alpha_{1}y_1y_1=- y_1\sum_{i=2}^{N} \alpha_{i} y_{i},∵y_1y_1=1,∴\alpha_{1}=-y_{1} \sum_{i=2}^{N} \alpha_{i} y_{i} α1y1=−∑i=2Nαiyi,α1y1y1=−y1∑i=2Nαiyi,∵y1y1=1,∴α1=−y1∑i=2Nαiyi
如果
α
2
\alpha_{2}
α2 确定, 那么
α
1
\alpha_{1}
α1 也随之确定。所以子问题中同时更新两个变量。
整个SMO 算法包括两个部分: 求解两个变量二次规划的解析方法和选择变量的启发式方法。
7.4.1 两个变量二次规划的求解方法
- 选择两个变量,其它变量固定
- SMO将对偶问题转化成一系列子问题:
min α 1 , α 2 W ( α 1 , α 2 ) 2 = 1 2 K 11 α 1 2 + 1 2 K 22 α 2 2 + y 1 y 2 K 12 α 1 α 2 − ( α 1 + α 2 ) + y 1 α 1 ∑ i = 3 N y i α i K i 1 + y 2 α 2 ∑ i = 3 N y i α i K i 2 s.t. α 1 y 1 + α 2 y 2 = − ∑ i = 3 N y i α i = ζ 0 ≤ α i ≤ C , i = 1 , 2 \begin{aligned} \min _{\alpha_{1}, \alpha_{2}} & \frac{W\left(\alpha_{1}, \alpha_{2}\right)}{2}=\frac{1}{2} K_{11} \alpha_{1}^{2}+\frac{1}{2} K_{22} \alpha_{2}^{2}+y_{1} y_{2} K_{12} \alpha_{1} \alpha_{2} \\ &-\left(\alpha_{1}+\alpha_{2}\right)+y_{1} \alpha_{1} \sum_{i=3}^{N} y_{i} \alpha_{i} K_{i 1}+y_{2} \alpha_{2} \sum_{i=3}^{N} y_{i} \alpha_{i} K_{i 2} \\ \text { s.t. } & \alpha_{1} y_{1}+\alpha_{2} y_{2}=-\sum_{i=3}^{N} y_{i} \alpha_{i}=\zeta \\ & 0 \leq \alpha_{i} \leq C, i=1,2 \end{aligned} α1,α2min s.t. 2W(α1,α2)=21K11α12+21K22α22+y1y2K12α1α2−(α1+α2)+y1α1i=3∑NyiαiKi1+y2α2i=3∑NyiαiKi2α1y1+α2y2=−i=3∑Nyiαi=ζ0≤αi≤C,i=1,2
- 根据约束条件, α 2 \alpha_{2} α2 可以表示成 α 1 \alpha_{1} α1 的函数
- 优化问题可以有解析解
- 基于初始可行解 α 1 old α 2 old \alpha_{1}^{\text {old }} \alpha_{2}^{\text {old }} α1old α2old , 可以得到 α 1 new α 2 new \alpha_{1}^{\text {new }} \alpha_{2}^{\text {new }} α1new α2new
min α 1 , α 2 W ( α 1 , α 2 ) = 1 2 K 11 α 1 2 + 1 2 K 22 α 2 2 + y 1 y 2 K 12 α 1 α 2 − ( α 1 + α 2 ) + y 1 α 1 ∑ i = 3 N y i α i K i 1 + y 2 α 2 ∑ i = 3 N y i α i K i 2 s.t. α 1 y 1 + α 2 y 2 = − ∑ i = 3 N y i α i = ζ 0 ≤ α i ≤ C , i = 1 , 2 \begin{array}{rl} \min _{\alpha_{1}, \alpha_{2}} & W\left(\alpha_{1}, \alpha_{2}\right)=\frac{1}{2} K_{11} \alpha_{1}^{2}+\frac{1}{2} K_{22} \alpha_{2}^{2}+y_{1} y_{2} K_{12} \alpha_{1} \alpha_{2} \\ & -\left(\alpha_{1}+\alpha_{2}\right)+y_{1} \alpha_{1} \sum_{i=3}^{N} y_{i} \alpha_{i} K_{i 1}+y_{2} \alpha_{2} \sum_{i=3}^{N} y_{i} \alpha_{i} K_{i 2} \\ \text { s.t. } & \alpha_{1} y_{1}+\alpha_{2} y_{2}=-\sum_{i=3}^{N} y_{i} \alpha_{i}=\zeta \\ & 0 \leq \alpha_{i} \leq C, i=1,2 \end{array} minα1,α2 s.t. W(α1,α2)=21K11α12+21K22α22+y1y2K12α1α2−(α1+α2)+y1α1∑i=3NyiαiKi1+y2α2∑i=3NyiαiKi2α1y1+α2y2=−∑i=3Nyiαi=ζ0≤αi≤C,i=1,2
-
两个变量,约束条件用二维空间中的图形表示

-
根据不等式条件 α 2 n e w \alpha_{2}^{n e w} α2new 的取值范围:
L ≤ α 2 new ≤ H L = max ( 0 , α 2 old − α 1 old ) H = min ( C , C + α 2 old − α 1 old ) \begin{gathered} L \leq \alpha_{2}^{\text {new }} \leq H \\ L=\max \left(0, \alpha_{2}^{\text {old }}-\alpha_{1}^{\text {old }}\right) \quad H=\min \left(C, C+\alpha_{2}^{\text {old }}-\alpha_{1}^{\text {old }}\right) \end{gathered} L≤α2new ≤HL=max(0,α2old −α1old )H=min(C,C+α2old −α1old )
∵ α 1 ∈ [ 0 , C ] ∴ k − α 1 ∈ [ k , k − C ] α 2 ∈ [ k , k − C ] α 2 ∈ [ α 1 + α 2 , α 1 + α 2 − C ] α 2 ∈ [ 0 , C ] } ⇒ L = max ( 0 , α 2 old − α 1 old ) H = min ( C , C + α 2 old − α 1 old ) ∵\alpha_1 \in [0,C]\\∴k-\alpha_1 \in [k,k-C]\\\alpha_2 \in [k,k-C]\\\left.\begin{matrix} \alpha_2 \in [\alpha_1+\alpha_2,\alpha_1+\alpha_2-C] \\ \alpha_2 \in [0,C] \end{matrix}\right\}\Rightarrow L=\max \left(0, \alpha_{2}^{\text {old }}-\alpha_{1}^{\text {old }}\right) \quad H=\min \left(C, C+\alpha_{2}^{\text {old }}-\alpha_{1}^{\text {old }}\right) ∵α1∈[0,C]∴k−α1∈[k,k−C]α2∈[k,k−C]α2∈[α1+α2,α1+α2−C]α2∈[0,C]}⇒L=max(0,α2old −α1old )H=min(C,C+α2old −α1old )
同理,如果 y 1 = y 2 y_1=y_2 y1=y2,则 L = max ( 0 , α 2 old + α 1 old − C ) , H = min ( C , α 2 old + α 1 old ) L=\max \left(0, \alpha_{2}^{\text {old }}+\alpha_{1}^{\text {old }}-C\right), \quad H=\min \left(C, \alpha_{2}^{\text {old }}+\alpha_{1}^{\text {old }}\right) L=max(0,α2old +α1old −C),H=min(C,α2old +α1old ) -
求解过程: 先求沿着约束方向未经剪辑时的 α 2 new , u n \alpha_{2}^{\text {new }, u n} α2new ,un 再求剪辑后的 α 2 new \alpha_{2}^{\text {new }} α2new
记: g ( x ) = ∑ i = 1 N α i y i K ( x i , x ) + b g(x)=\sum_{i=1}^{N} \alpha_{i} y_{i} K\left(x_{i}, x\right)+b g(x)=∑i=1NαiyiK(xi,x)+b
令: E i = g ( x i ) − y i = ( ∑ j = 1 N α j y j K ( x j , x i ) + b ) − y i , i = 1 , 2 \text { 令: } \quad E_{i}=g\left(x_{i}\right)-y_{i}=\left(\sum_{j=1}^{N} \alpha_{j} y_{j} K\left(x_{j}, x_{i}\right)+b\right)-y_{i}, \quad i=1,2 令: Ei=g(xi)−yi=(j=1∑NαjyjK(xj,xi)+b)−yi,i=1,2E E E 为输入 x x x 的预测值和真实输出 y y y 的差, i = 1 , 2 i=1,2 i=1,2
引进记号
v i = ∑ j = 3 N α j y j K ( x i , x j ) = g ( x i ) − ∑ j = 1 2 α j y j K ( x i , x j ) − b , i = 1 , 2 v_{i}=\sum_{j=3}^{N} \alpha_{j} y_{j} K\left(x_{i}, x_{j}\right)=g\left(x_{i}\right)-\sum_{j=1}^{2} \alpha_{j} y_{j} K\left(x_{i}, x_{j}\right)-b, i=1,2 vi=j=3∑NαjyjK(xi,xj)=g(xi)−j=1∑2αjyjK(xi,xj)−b,i=1,2目标函数可写成
W ( α 1 , α 2 ) = 1 2 K 11 α 1 2 + 1 2 K 22 α 2 2 + y 1 y 2 K 12 α 1 α 2 − ( α 1 + α 2 ) + y 1 v 1 α 1 + y 2 v 2 α 2 \begin{aligned} W\left(\alpha_{1}, \alpha_{2}\right)=& \frac{1}{2} K_{11} \alpha_{1}^{2}+\frac{1}{2} K_{22} \alpha_{2}^{2}+y_{1} y_{2} K_{12} \alpha_{1} \alpha_{2}-\\ &\left(\alpha_{1}+\alpha_{2}\right)+y_{1} v_{1} \alpha_{1}+y_{2} v_{2} \alpha_{2} \end{aligned} W(α1,α2)=21K11α12+21K22α22+y1y2K12α1α2−(α1+α2)+y1v1α1+y2v2α2由 α 1 y 1 = ς − α 2 y 2 \alpha_{1} y_{1}=\varsigma-\alpha_{2} y_{2} α1y1=ς−α2y2 及 y i 2 = 1 y_{i}^{2}=1 yi2=1, 可将 α 1 \alpha_{1} α1 表示为
α 1 = ( ς − y 2 α 2 ) y 1 \alpha_{1}=\left(\varsigma-y_{2} \alpha_{2}\right) y_{1} α1=(ς−y2α2)y1代入式 W ( α 1 , α 2 ) = 1 2 K 11 α 1 2 + 1 2 K 22 α 2 2 + y 1 y 2 K 12 α 1 α 2 − ( α 1 + α 2 ) + y 1 v 1 α 1 + y 2 v 2 α 2 \begin{aligned} W\left(\alpha_{1}, \alpha_{2}\right)=& \frac{1}{2} K_{11} \alpha_{1}{2}+\frac{1}{2} K_{22} \alpha_{2}{2}+y_{1} y_{2} K_{12} \alpha_{1} \alpha_{2}-\\ &\left(\alpha_{1}+\alpha_{2}\right)+y_{1} v_{1} \alpha_{1}+y_{2} v_{2} \alpha_{2} \end{aligned} W(α1,α2)=21K11α12+21K22α22+y1y2K12α1α2−(α1+α2)+y1v1α1+y2v2α2, 得到只是 α 2 \alpha_{2} α2 的函数的目标函数:
W ( α 2 ) = 1 2 K 11 ( ς − α 2 y 2 ) 2 + 1 2 K 22 α 2 2 + y 2 K 12 ( ς − α 2 y 2 ) α 2 − ( ς − α 2 y 2 ) y 1 − α 2 + v 1 ( ς − α 2 y 2 ) + y 2 v 2 α 2 \begin{aligned} W\left(\alpha_{2}\right)=& \frac{1}{2} K_{11}\left(\varsigma-\alpha_{2} y_{2}\right)^{2}+\frac{1}{2} K_{22} \alpha_{2}^{2}+y_{2} K_{12}\left(\varsigma-\alpha_{2} y_{2}\right) \alpha_{2}-\\ &\left(\varsigma-\alpha_{2} y_{2}\right) y_{1}-\alpha_{2}+v_{1}\left(\varsigma-\alpha_{2} y_{2}\right)+y_{2} v_{2} \alpha_{2} \end{aligned} W(α2)=21K11(ς−α2y2)2+21K22α22+y2K12(ς−α2y2)α2−(ς−α2y2)y1−α2+v1(ς−α2y2)+y2v2α2对 α 2 \alpha_{2} α2 求导数
∂ W ∂ α 2 = K 11 α 2 + K 22 α 2 − 2 K 12 α 2 − K 11 ς y 2 + K 12 ς y 2 + y 1 y 2 − 1 − v 1 y 2 + y 2 v 2 \begin{aligned} \frac{\partial W}{\partial \alpha_{2}}=& K_{11} \alpha_{2}+K_{22} \alpha_{2}-2 K_{12} \alpha_{2}-\\ & K_{11} \varsigma y_{2}+K_{12} \varsigma y_{2}+y_{1} y_{2}-1-v_{1} y_{2}+y_{2} v_{2} \end{aligned} ∂α2∂W=K11α2+K22α2−2K12α2−K11ςy2+K12ςy2+y1y2−1−v1y2+y2v2令其为 0 , 得到
( K 11 + K 22 − 2 K 12 ) α 2 = y 2 ( y 2 − y 1 + ς K 11 − ς K 12 + v 1 − v 2 ) = y 2 [ y 2 − y 1 + ς K 11 − ς K 12 + ( g ( x 1 ) − ∑ j = 1 2 y j α j K 1 j − b ) − ( g ( x 2 ) − ∑ j = 1 2 y j α j K 2 j − b ) ] \begin{aligned} \left(K_{11}+K_{22}-2 K_{12}\right) \alpha_{2}=& y_{2}\left(y_{2}-y_{1}+\varsigma K_{11}-\varsigma K_{12}+v_{1}-v_{2}\right) \\ =& y_{2}\left[y_{2}-y_{1}+\varsigma K_{11}-\varsigma K_{12}+\left(g\left(x_{1}\right)-\sum_{j=1}^{2} y_{j} \alpha_{j} K_{1 j}-b\right)-\right.\\ &\left.\left(g\left(x_{2}\right)-\sum_{j=1}^{2} y_{j} \alpha_{j} K_{2 j}-b\right)\right] \end{aligned} (K11+K22−2K12)α2==y2(y2−y1+ςK11−ςK12+v1−v2)y2[y2−y1+ςK11−ςK12+(g(x1)−j=1∑2yjαjK1j−b)−(g(x2)−j=1∑2yjαjK2j−b)]将 ς = α 1 old y 1 + α 2 old y 2 \varsigma=\alpha_{1}^{\text {old }} y_{1}+\alpha_{2}^{\text {old }} y_{2} ς=α1old y1+α2old y2 代入, 得到
( K 11 + K 22 − 2 K 12 ) α 2 new , unc = y 2 ( ( K 11 + K 22 − 2 K 12 ) α 2 old y 2 + y 2 − y 1 + g ( x 1 ) − g ( x 2 ) ) = ( K 11 + K 22 − 2 K 12 ) α 2 old + y 2 ( E 1 − E 2 ) \begin{aligned} \left(K_{11}+K_{22}-2 K_{12}\right) \alpha_{2}^{\text {new }, \text { unc }} &=y_{2}\left(\left(K_{11}+K_{22}-2 K_{12}\right) \alpha_{2}^{\text {old }} y_{2}+y_{2}-y_{1}+g\left(x_{1}\right)-g\left(x_{2}\right)\right) \\ &=\left(K_{11}+K_{22}-2 K_{12}\right) \alpha_{2}^{\text {old }}+y_{2}\left(E_{1}-E_{2}\right) \end{aligned} (K11+K22−2K12)α2new , unc =y2((K11+K22−2K12)α2old y2+y2−y1+g(x1)−g(x2))=(K11+K22−2K12)α2old +y2(E1−E2)将 η = K 11 + K 22 − 2 K 12 \eta=K_{11}+K_{22}-2 K_{12} η=K11+K22−2K12 代入, 于是得到
α 2 new,unc = α 2 old + y 2 ( E 1 − E 2 ) η \alpha_{2}^{\text {new,unc }}=\alpha_{2}^{\text {old }}+\frac{y_{2}\left(E_{1}-E_{2}\right)}{\eta} α2new,unc =α2old +ηy2(E1−E2)得到:
最优化子问题沿约束方向未经前辑的解:
α 2 n e w , u n c = α 2 o l d + y 2 ( E 1 − E 2 ) η η = K 11 + K 22 − 2 K 12 = ∥ Φ ( x 1 ) − Φ ( x 2 ) ∥ 2 \begin{gathered} \alpha_{2}^{n e w, u n c}=\alpha_{2}^{o l d}+\frac{y_{2}\left(E_{1}-E_{2}\right)}{\eta} \\ \eta=K_{11}+K_{22}-2 K_{12}=\left\|\Phi\left(x_{1}\right)-\Phi\left(x_{2}\right)\right\|^{2} \end{gathered} α2new,unc=α2old+ηy2(E1−E2)η=K11+K22−2K12=∥Φ(x1)−Φ(x2)∥2剪辑后的解 α 2 n e w = { H , a m p ; α 2 n e w , u n c g t ; H α 2 n e w , u n c , a m p ; L ≤ α 2 n e w , u n c ≤ H L , a m p ; α 2 n e w , u n c l t ; L \begin{array}{r}\text { 剪辑后的解 } \\ \alpha_{2}^{n e w}\end{array}=\left\{\begin{array}{rr}H, & \alpha_{2}^{n e w, u n c}>H \\ \alpha_{2}^{n e w, u n c}, & L \leq \alpha_{2}^{n e w, u n c} \leq H \\ L, & \alpha_{2}^{n e w, u n c}<L\end{array}\right. 剪辑后的解 α2new=⎩⎨⎧H,α2new,unc,L,amp;α2new,uncamp;L≤α2new,unc≤Hamp;α2new,uncgt;Hlt;L
得到 α 1 \alpha_{1} α1 的解 α 1 n e w = α 1 old + y 1 y 2 ( α 2 old − α 2 new ) \quad \alpha_{1}^{n e w}=\alpha_{1}^{\text {old }}+y_{1} y_{2}\left(\alpha_{2}^{\text {old }}-\alpha_{2}^{\text {new }}\right) α1new=α1old +y1y2(α2old −α2new )
计算阈值 b b b 和差值 E i E_{i} Ei
在每次完成两个变量的优化后, 都要重新计算阈值 b b b 。当 0 < α 1 new < C 0<\alpha_{1}^{\text {new }}<C 0<α1new <C 时, 由 KKT 条件 0 < α i < C ⇔ y i g ( x i ) = 1 0<\alpha_{i}<C \Leftrightarrow y_{i} g\left(x_{i}\right)=1 0<αi<C⇔yig(xi)=1可知:
∑ i = 1 N α i y i K i 1 + b = y 1 \sum_{i=1}^{N} \alpha_{i} y_{i} K_{i 1}+b=y_{1} i=1∑NαiyiKi1+b=y1于是,
b 1 new = y 1 − ∑ i = 3 N α i y i K i 1 − α 1 new y 1 K 11 − α 2 new y 2 K 21 b_{1}^{\text {new }}=y_{1}-\sum_{i=3}^{N} \alpha_{i} y_{i} K_{i 1}-\alpha_{1}^{\text {new }} y_{1} K_{11}-\alpha_{2}^{\text {new }} y_{2} K_{21} b1new =y1−i=3∑NαiyiKi1−α1new y1K11−α2new y2K21由 E 1 E_{1} E1 的定义式 E i = g ( x i ) − y i = ( ∑ j = 1 N α j y j K ( x j , x i ) + b ) − y i , i = 1 , 2 E_{i}=g\left(x_{i}\right)-y_{i}=\left(\sum_{j=1}^{N} \alpha_{j} y_{j} K\left(x_{j}, x_{i}\right)+b\right)-y_{i}, \quad i=1,2 Ei=g(xi)−yi=(∑j=1NαjyjK(xj,xi)+b)−yi,i=1,2 有
E 1 = ∑ i = 3 N α i y i K i 1 + α 1 old y 1 K 11 + α 2 old y 2 K 21 + b old − y 1 E_{1}=\sum_{i=3}^{N} \alpha_{i} y_{i} K_{i 1}+\alpha_{1}^{\text {old }} y_{1} K_{11}+\alpha_{2}^{\text {old }} y_{2} K_{21}+b^{\text {old }}-y_{1} E1=i=3∑NαiyiKi1+α1old y1K11+α2old y2K21+bold −y1式 b 1 new = y 1 − ∑ i = 3 N α i y i K i 1 − α 1 new y 1 K 11 − α 2 new y 2 K 21 b_{1}^{\text {new }}=y_{1}-\sum_{i=3}^{N} \alpha_{i} y_{i} K_{i 1}-\alpha_{1}^{\text {new }} y_{1} K_{11}-\alpha_{2}^{\text {new }} y_{2} K_{21} b1new =y1−∑i=3NαiyiKi1−α1new y1K11−α2new y2K21 的前两项可写成:
y 1 − ∑ i = 3 N α i y i K i 1 = − E 1 + α 1 old y 1 K 11 + α 2 old y 2 K 21 + b old y_{1}-\sum_{i=3}^{N} \alpha_{i} y_{i} K_{i 1}=-E_{1}+\alpha_{1}^{\text {old }} y_{1} K_{11}+\alpha_{2}^{\text {old }} y_{2} K_{21}+b^{\text {old }} y1−i=3∑NαiyiKi1=−E1+α1old y1K11+α2old y2K21+bold代入式 b 1 new = y 1 − ∑ i = 3 N α i y i K i 1 − α 1 new y 1 K 11 − α 2 new y 2 K 21 b_{1}^{\text {new }}=y_{1}-\sum_{i=3}^{N} \alpha_{i} y_{i} K_{i 1}-\alpha_{1}^{\text {new }} y_{1} K_{11}-\alpha_{2}^{\text {new }} y_{2} K_{21} b1new =y1−∑i=3NαiyiKi1−α1new y1K11−α2new y2K21, 可得
b 1 new = − E 1 − y 1 K 11 ( α 1 new − α 1 old ) − y 2 K 21 ( α 2 new − α 2 old ) + b old b_{1}^{\text {new }}=-E_{1}-y_{1} K_{11}\left(\alpha_{1}^{\text {new }}-\alpha_{1}^{\text {old }}\right)-y_{2} K_{21}\left(\alpha_{2}^{\text {new }}-\alpha_{2}^{\text {old }}\right)+b^{\text {old }} b1new =−E1−y1K11(α1new −α1old )−y2K21(α2new −α2old )+bold同样, 如果 0 < α 2 new < C 0<\alpha_{2}^{\text {new }}<C 0<α2new <C, 那么,
b 2 new = − E 2 − y 1 K 12 ( α 1 new − α 1 old ) − y 2 K 22 ( α 2 new − α 2 old ) + b old b_{2}^{\text {new }}=-E_{2}-y_{1} K_{12}\left(\alpha_{1}^{\text {new }}-\alpha_{1}^{\text {old }}\right)-y_{2} K_{22}\left(\alpha_{2}^{\text {new }}-\alpha_{2}^{\text {old }}\right)+b^{\text {old }} b2new =−E2−y1K12(α1new −α1old )−y2K22(α2new −α2old )+bold如果 α 1 new , α 2 new \alpha_{1}^{\text {new }}, \alpha_{2}^{\text {new }} α1new ,α2new 同时满足条件 0 < α i new < C , i = 1 , 2 0<\alpha_{i}^{\text {new }}<C, i=1,2 0<αinew <C,i=1,2, 那么 b 1 new = b 2 new b_{1}^{\text {new }}=b_{2}^{\text {new }} b1new =b2new 。如果 α 1 new , α 2 new \alpha_{1}^{\text {new }}, \alpha_{2}^{\text {new }} α1new ,α2new 是 0 或者 C C C, 那么 b 1 new b_{1}^{\text {new }} b1new 和 b 2 new b_{2}^{\text {new }} b2new 以及它们之间的数都是符合 KKT 条件的 阈值, 这时选择它们的中点作为 b new b^{\text {new }} bnew 。
在每次完成两个变量的优化之后, 还必须更新对应的 E i E_{i} Ei 值, 并将它们保存在列 表中。 E i E_{i} Ei 值的更新要用到 b new b^{\text {new }} bnew 值, 以及所有支持向量对应的 α j \alpha_{j} αj :
E i new = ∑ S y j α j K ( x i , x j ) + b new − y i E_{i}^{\text {new }}=\sum_{S} y_{j} \alpha_{j} K\left(x_{i}, x_{j}\right)+b^{\text {new }}-y_{i} Einew =S∑yjαjK(xi,xj)+bnew −yi其中, S S S 是所有支持向量 x j x_{j} xj 的集合。
7.4.2 变量的选择方法
SMO算法在每个子问题中选择两个变量优化, 其中至少一个变量是违反KKT条件的
- 第一个变量的选择:外循环
- 违反KKT最严重的样本点,
- 检验样本点是否满足KKT条件:
α i = 0 ↔ y i g ( x i ) ≥ 1 0 < α i < C ↔ y i g ( x i ) ≤ 1 α i = C ↔ y i g ( x i ) ≤ 1 g ( x i ) = ∑ j = 1 N α j y j K ( x i , x j ) + b \begin{aligned} &\alpha_{i}=0 \leftrightarrow y_{i} g\left(x_{i}\right) \geq 1 \\ &0<\alpha_{i}<C \leftrightarrow y_{i} g\left(x_{i}\right) \leq 1 \\ &\alpha_{i}=C \leftrightarrow y_{i} g\left(x_{i}\right) \leq 1 \\ &g\left(x_{i}\right)=\sum_{j=1}^{N} \alpha_{j} y_{j} K\left(x_{i}, x_{j}\right)+b \end{aligned} αi=0↔yig(xi)≥10<αi<C↔yig(xi)≤1αi=C↔yig(xi)≤1g(xi)=j=1∑NαjyjK(xi,xj)+b
2、第二个变量的检查:内循环,
- 选择的标准是希望能使目标函数有足够大的变化
- 即对应 ∣ E 1 − E 2 ∣ \left|E_{1}-E_{2}\right| ∣E1−E2∣ 最大,即 E 1 , E 2 E_{1}, E_{2} E1,E2 的符号相反, 差异最大
- 如果内循环通过上述方法找到的点不能使目标函数有足够的下降
- 则:遍历间隔边界上的样本点, 测试目标函数下降
- 如果下降不大, 则遍历所有样本点
- 如果依然下降不大,则丢弃外循环点,重新选择
SMO 算法
输入: 训练数据集
T
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
⋯
,
(
x
N
,
y
N
)
}
T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{N}, y_{N}\right)\right\}
T={(x1,y1),(x2,y2),⋯,(xN,yN)}, 其中,
x
i
∈
X
=
R
n
x_{i} \in \mathcal{X}=\mathbf{R}^{n}
xi∈X=Rn,
y
i
∈
Y
=
{
−
1
,
+
1
}
,
i
=
1
,
2
,
⋯
,
N
y_{i} \in \mathcal{Y}=\{-1,+1\}, i=1,2, \cdots, N
yi∈Y={−1,+1},i=1,2,⋯,N, 精度
ε
;
\varepsilon ;
ε;
输出: 近似解
α
^
∘
\hat{\alpha}_{\circ}
α^∘
1、取初值
α
(
0
)
=
0
\alpha^{(0)}=0
α(0)=0, 令
k
=
0
k=0
k=0;
2、选取优化变量
α
1
(
k
)
,
α
2
(
k
)
\alpha_{1}^{(k)}, \alpha_{2}^{(k)}
α1(k),α2(k), 解析求解两个变量的最优化问题
min
α
1
,
α
2
W
(
α
1
,
α
2
)
=
1
2
K
11
α
1
2
+
1
2
K
22
α
2
2
+
y
1
y
2
K
12
α
1
α
2
−
(
α
1
+
α
2
)
+
y
1
α
1
∑
i
=
3
N
y
i
α
i
K
i
1
+
y
2
α
2
∑
i
=
3
N
y
i
α
i
K
i
2
s.t.
α
1
y
1
+
α
2
y
2
=
−
∑
i
=
3
N
y
i
α
i
=
ζ
0
≤
α
i
≤
C
,
i
=
1
,
2
\begin{array}{rl}\min _{\alpha_{1}, \alpha_{2}} & W\left(\alpha_{1}, \alpha_{2}\right)=\frac{1}{2} K_{11} \alpha_{1}^{2}+\frac{1}{2} K_{22} \alpha_{2}^{2}+y_{1} y_{2} K_{12} \alpha_{1} \alpha_{2} \\& -\left(\alpha_{1}+\alpha_{2}\right)+y_{1} \alpha_{1} \sum_{i=3}^{N} y_{i} \alpha_{i} K_{i 1}+y_{2} \alpha_{2} \sum_{i=3}^{N} y_{i} \alpha_{i} K_{i 2} \\\text { s.t. } & \alpha_{1} y_{1}+\alpha_{2} y_{2}=-\sum_{i=3}^{N} y_{i} \alpha_{i}=\zeta \\& 0 \leq \alpha_{i} \leq C, i=1,2\end{array}
minα1,α2 s.t. W(α1,α2)=21K11α12+21K22α22+y1y2K12α1α2−(α1+α2)+y1α1∑i=3NyiαiKi1+y2α2∑i=3NyiαiKi2α1y1+α2y2=−∑i=3Nyiαi=ζ0≤αi≤C,i=1,2, 求得最优解
α
1
(
k
+
1
)
,
α
2
(
k
+
1
)
\alpha_{1}^{(k+1)}, \alpha_{2}^{(k+1)}
α1(k+1),α2(k+1), 更新
α
\alpha
α 为
α
(
k
+
1
)
\alpha^{(k+1)}
α(k+1);
3、若在精度
ε
\varepsilon
ε 范围内满足停机条件
∑ i = 1 N α i y i = 0 , 0 ⩽ α i ⩽ C , i = 1 , 2 , ⋯ , N y i ⋅ g ( x i ) { ⩾ 1 , { x i ∣ α i = 0 } = 1 , { x i ∣ 0 < α i < C } ⩽ 1 , { x i ∣ α i = C } \begin{aligned} &\sum_{i=1}^{N} \alpha_{i} y_{i}=0, \quad 0 \leqslant \alpha_{i} \leqslant C, \quad i=1,2, \cdots, N \\ &y_{i} \cdot g\left(x_{i}\right) \begin{cases}\geqslant 1, & \left\{x_{i} \mid \alpha_{i}=0\right\} \\ =1, & \left\{x_{i} \mid 0<\alpha_{i}<C\right\} \\ \leqslant 1, & \left\{x_{i} \mid \alpha_{i}=C\right\}\end{cases} \end{aligned} i=1∑Nαiyi=0,0⩽αi⩽C,i=1,2,⋯,Nyi⋅g(xi)⎩⎪⎨⎪⎧⩾1,=1,⩽1,{xi∣αi=0}{xi∣0<αi<C}{xi∣αi=C}
其中,
g ( x i ) = ∑ j = 1 N α j y j K ( x j , x i ) + b g\left(x_{i}\right)=\sum_{j=1}^{N} \alpha_{j} y_{j} K\left(x_{j}, x_{i}\right)+b g(xi)=j=1∑NαjyjK(xj,xi)+b
则转 4; 否则令
k
=
k
+
1
k=k+1
k=k+1, 转 (2);
4、取
α
^
=
α
(
k
+
1
)
\hat{\alpha}=\alpha^{(k+1)}
α^=α(k+1) 。



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










