具有自适应距离对齐的时空步态特征
paper题目:Spatio-temporal Gait Feature with Adaptive Distance Alignment
paper是IEEE Fellow Xuelong Li发表在arxiv 2022的工作
paper地址:链接
Abstract
步态识别是一项重要的识别技术,因为它不易伪装,识别目标不需要合作。然而,步态识别仍然存在严重挑战,即步行姿势相似的人经常被错误识别。本文尝试从网络结构的优化和提取的步态特征的细化两个方面来增加不同目标的步态特征差异,从而提高对具有相似步行姿势的目标的识别效率。因此我出了本文的方法,它由时空特征提取 (SFE) 和自适应距离对齐 (ADA) 组成,其中 SFE 使用时间特征融合 (TFF) 和细粒度特征提取 (FFE) 从原始轮廓中有效地提取时空特征, ADA 以现实生活中大量未标记的步态数据为基准,对提取的时空特征进行细化,使其类间相似度低,类内相似度高。在 mini-OUMVLP 和 CASIA-B 上的大量实验证明,本文的结果比一些最先进的方法要好。
关键词——步态识别、时空特征提取、特征调整。
I. INTRODUCTION
与虹膜、指纹、人脸等生物特征不同,步态在识别过程中不需要目标的配合,在不受控制的场景下可以远距离识别目标。因此,步态在法医鉴定、视频监控、犯罪侦查等方面有着广泛的应用。作为一项视觉识别任务,其目的是学习不同目标的判别特征。然而,从原始步态序列中学习时空特征时,经常会受到许多外部因素的干扰,例如各种相机角度、不同的衣服/携带条件。
已经提出了许多基于深度学习的方法来克服这些问题。 DVGan 使用 GAN 生成整个时角空间,其视角从 0° 到 180°,间隔为 1°,以适应各种摄像机角度。 GaitNet 使用自编码器作为他们的框架来从原始 RGB 图像中学习与步态相关的信息。它还使用 LSTM 来学习时间信息的变化,以克服不同的衣服/携带条件。 GaitSet从由独立帧组成的集合中学习身份信息,以适应各种视角和不同的衣服/携带条件。 Gaitpart采用部分特征进行人体描述,以增强细粒度学习。
以往的方法要么只关注时间特征的处理,要么只关注细粒度特征的提取,不能保证同时充分提取时空信息。为了解决这个问题,尝试使用时间特征融合(TFF)融合最具代表性的时间特征,然后使用细粒度特征提取(FFE)从最具代表性的时间特征中提取细粒度特征,经过这些操作,可以完全提取原始步态轮廓的时空特征。然而,当遇到两个行走姿势相似的目标时,完美的网络结构只能保证充分提取他们的步态特征,而不能保证他们的判别力。为了解决这个问题,作者尝试使用自适应距离对齐技术从未标记的数据中自适应地选择合适的基准来细化提取的时空特征,该操作可以有效地增加具有相似步行的受试者的步态特征差异。因此,提出了方法:具有自适应距离对齐的时空步态特征,它由时空特征提取(SFE)和自适应距离对齐(ADA)组成。 SFE 包括 FFE 和 TFF。
具体来说,每个初始帧都已输入到 TFF 中,以通过最大池化选择最具代表性的时间特征。在此之后,作者将融合的最具代表性的时间特征分成 4 个块,并使用单个卷积层来提取细粒度特征。最后,使用 ADA 对提取的时空特征进行细化,使其具有低类间相似度和高类内相似度。
将从以下三个方面描述所提出方法的优点:
-
在 TFF 使用最大池化来融合最具代表性的时间特征,然后将最具代表性的时间特征分成 4 个块来提取细粒度的空间特征。这部分使用了一个简化的时空特征提取模块,可以有效地学习原始步态序列的时空特征。
-
改进了距离对齐技术并将其应用于步态识别领域。改进的距离对齐技术采用自适应的方法从现实生活中未标记的数据集中选择合适的基准,然后利用该基准对提取的时空特征进行细化,可以有效增加具有相似步行姿势的受试者的步态特征差异。
-
提出了一种称为具有自适应距离对齐的时空步态特征的方法。它可以有效地从原始步态轮廓中提取时空特征,增加不同目标之间的差异。对 CASIA-B 和 mini-OUMVLP 的大量实验证明,本文的方法比其他最先进的方法具有更好的结果。值得注意的是,本文的方法在正常步行条件下的 CASIA-B 步态数据集上实现了 97.0% 的平均 rank-1 准确度。
II. RELATED WORK
这部分主要介绍步态识别的相关工作,将从以下几个方面入手:步态识别的主要方法、从原始步态轮廓中学习时空信息的方法的演变以及距离对齐的启发。
步态识别。目前的步态识别方法可以分为基于模型的方法和基于外观的方法。基于外观的方法通过卷积神经网络(CNN)直接从步态序列中的原始轮廓中学习时空特征,然后通过特征匹配来判断步态序列的目标身份。基于模型的方法首先对步态序列中的原始轮廓进行建模,然后使用一种新的方式来表达原始轮廓,并学习它们的时空特征。一个具有代表性的基于模型的方法是JointsGait,它使用原始步态轮廓的人体关节来创建步态图结构,然后通过图卷积网络 (GCN) 从步态图结构中提取时空特征。然而,当用这种方法来表达步态序列中的轮廓时,往往会丢失很多重要的细节信息,增加识别难度。而其他基于模型的方法也遇到了这个问题,所以基于外观的方法已经成为目前最主流的步态识别方法。本文后面提到的方法都属于基于外观的方法。
时空特征提取模块。时空特征提取的效率是衡量基于外观的方法质量的重要因素,它会影响识别的准确性。时空特征提取模块可以分为两部分:空间特征提取模块和时间特征提取模块。
对于时间特征提取模块,有基于深度学习的方法和传统方法。传统方法首先通过一些操作将原始步态轮廓压缩成一张图像,例如 GEI、PEI 和 CGI。然后使用神经网络从该图像中提取时空特征。虽然这些传统方法很简单。以下研究人员发现他们不能很好地保存时间信息,并尝试使用基于深度学习的方法来提取时间特征。 LSTM使用重复的神经网络模块来保存和提取原始步态序列的时间信息。 GaitSet观察到即使步态序列被打乱,将它们重新排列成正确的顺序并不困难,然后使用打乱的轮廓来学习时空信息,以确保各种步态序列的适应性。但是 LSTM 和 GaitSet 都有一些缺点:它们的网络结构和计算过程复杂。本文尝试使用多个并行卷积层从原始步态轮廓中提取全局特征,并使用简单的最大池化操作来融合最具代表性的时间特征。这样可以简化网络结构,减少计算量,有效提取时间特征。值得注意的是,本文的方法总共只使用了 4 个卷积层和 2 个池化层。
对于空间特征提取模块,在[43]中,在步态识别中引入了partial的思想,认为不同的人体部位在身份信息的识别中会起到不同的作用。因此,将人体分为七个不同的部分,通过去除平均步态图像中的七个部位并观察识别率的变化来探索不同部位对步态识别的影响。为目前局部思想的使用奠定了基础。 GaitPart在深度学习领域利用这种思想对人体进行描述,充分提取细粒度信息,将多层特征分块提取细粒度特征,取得了很好的效果。但是,GaitPart 采用了partial in shallow features 的思想,将多层特征划分为block,增加了网络的复杂度。本文只对高层特征进行一次划分以提取细粒度特征,并且仅使用单个卷积层可以获得良好的性能。它还大大简化了网络结构。
自适应距离对齐。距离对齐技术首先用于细化人脸特征,具有良好的性能。它使用大量未标注数据来判断真实场景中特征分布的流行密度,并以此密度为基准对提取的时空特征进行细化,将收敛性差的特征收敛到一起,将特征分散收敛得太紧。人脸识别任务和步态识别任务的本质目的都是通过特征匹配来识别目标的身份。由于这两个任务的相似性,作者尝试改进距离对齐技术并将其引入步态识别领域。前面的距离对齐首先计算未标记数据集中的特征与图库集和探针集中提取的时空特征之间的距离,然后通过计算距离从未标记数据中选择一些与提取的时空特征相似的特征,它从这些相似特征中选择最大值作为基准来细化提取的时空特征。这种操作可以达到很好的效果,但是它只使用了这些特征与未标记数据中提取的时空特征相似的最大值,因此这些相似特征没有被充分利用。本文尽量充分利用这些相似的特征,适应性从整体(mean)、最大(maximum)、最适中(median)三个方面选择最合适的benchmark,达到最好的细化效果。将改进的距离对齐称为自适应距离对齐技术。
结合时空特征提取模块的发展和距离对齐的启发,提出了一种方法:时空步态特征与自适应距离对齐。它使用最大池化来融合最具代表性的时间特征,在高级特征上引入部分思想,改进距离对齐,并将其引入步态识别。它不仅通过时空特征提取模块有效地从原始步态轮廓中提取时空特征,而且使用自适应距离对齐技术对提取的时空特征进行细化,以增加不同目标之间步态特征的区分度。
III. OUR METHOD
这一部分将从三个方面介绍本文的方法:包括整体流水线、时空特征提取(SFE)模块和自适应距离对齐(ADA),其中时空特征提取主要包括两部分:粒度特征提取(FFE)和时间特征融合(TFF)。所提出方法的框架如图1所示。
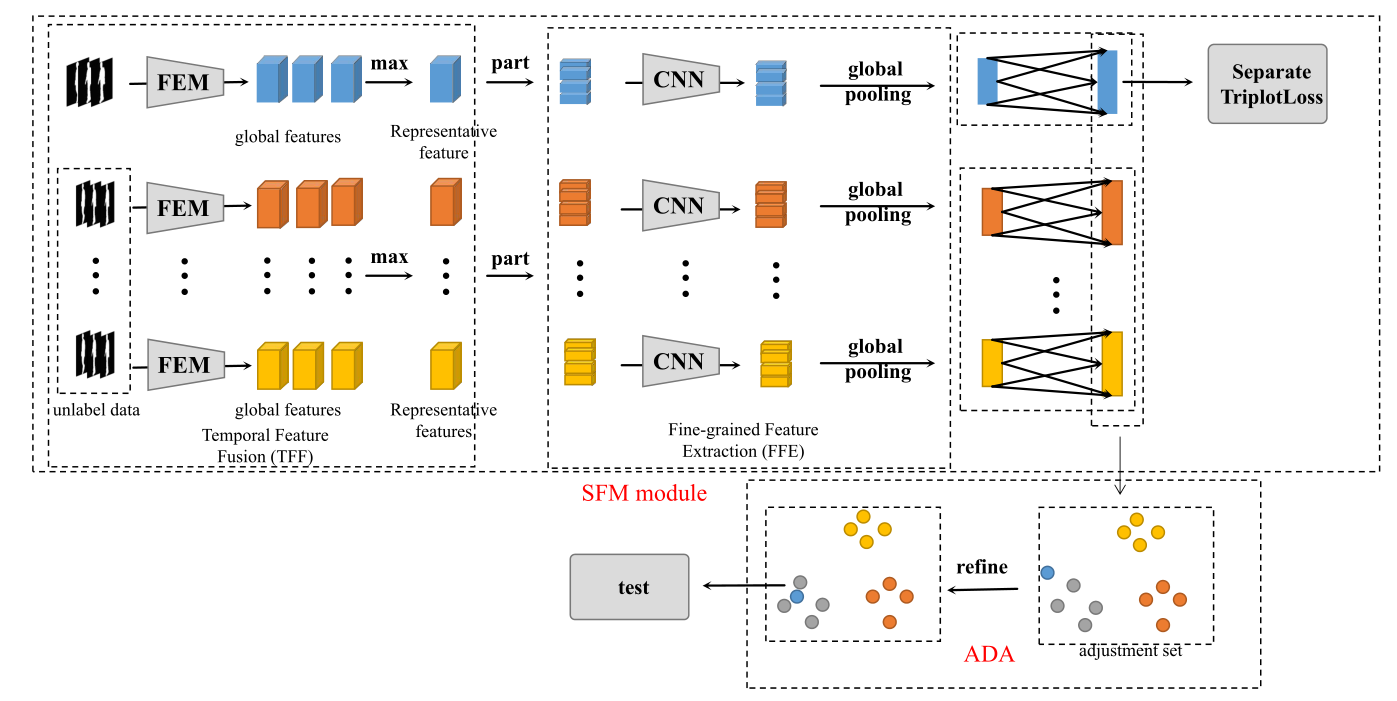
图 1. 本文方法的框架。可以清楚地观察到,本文的框架由两部分组成:时空特征提取(SFE)模块和自适应距离对齐(ADA)。 SFE模块主要是神经网络结构的优化。 ADA是对图库集和探针集中提取的时空特征的细化。在图的底部,为了方便查看特征的分布,用圆圈来表示特征。
A. Pipeline
如图 1 所示,本文的网络主要由两部分组成:SFE 模块和 ADA。 SFE模块主要是神经网络结构的优化,它可以通过简单的网络结构有效地提取原始步态序列的时空特征。 ADA是一种后处理方法,主要以现实生活中大量未标记的步态数据为基准,对提取的时空特征进行细化,可以增加不同目标间步态特征的差异。
具体来说,在 SFE 部分,首先将一些原始步态轮廓逐帧输入到 TFF。 TFF 使用 Feature Extraction Module (FEM) 来学习每一帧的全局信息,FEM 只包含 4 个卷积层和 2 个 Max pooling 层,它可以保证每一帧的详细信息都能被充分学习,然后使用简单的操作max从提取的全局特征中融合最具代表性的时间特征。它可以在保证时间信息被充分提取的同时简化网络结构,减少计算量。在 TFF 之后,将最具代表性的时间特征输入到 FFE 以学习细粒度特征。代表帧首先被分为 4 个部分,然后仅使用一个卷积层来学习其细粒度信息。 TFF 和 FFE 都使用简单的网络结构。然后将提取的时空特征输入到下一部分。这部分使用由max pooling和mean pooling组成的Global Pooling来选择从每个块中提取的合适的细粒度特征。全连接层在全局池化之后,它可以整合之前提取的特征。最后,使用hard三元组损失作为微调网络参数的限制。
在 ADA 部分,首先从现实生活中找到大量未标记的步态数据,然后使用经过训练的 SFE 模块从未标记的步态数据集中提取时空特征,并将这些提取的时空特征作为调整集。然后计算调整集中这些特征与从原始步态序列中提取的时空特征之间的距离,并通过计算的距离从调整集中选择4个与提取的时空特征相似的特征。最后,适应性的从这些选择的特征中从整体(mean)、最大(maximum)和最适中(median)三个方面选择最合适的基准,并使用基准来细化提取的时空特征。
B. Spatio-temporal Feature Extraction module
这部分提出的模块主要是试图简化神经网络的结构,减少计算量,同时保证原始步态序列的时空特征能够被充分提取。将从 TFF 和 FEE 来介绍:其中 FFE 表示 Fine-grained Feature Extraction,TFF 表示 Temporal Feature Fusion。
- 时间特征融合:TFF 由多个并行 FEM 和一个最大池化层组成,其中 FEM 的参数是共享的。 FEMs用于从每一帧中提取全局特征,它们可以充分提取每一帧的重要信息。最大池化用于从每帧提取的全局特征中选择最具代表性的时间特征。接下来将介绍 FEM 的结构以及可以做些什么来有效地融合这些复杂的时间信息以获得最具代表性的时间特征。
如表1所示,FEM 仅使用 4 个卷积层来提取原始轮廓的全局特征,并使用 2 个 Max pooling 层来选择这些全局特征的重要信息。这些操作可以充分提取每一帧的全局特征。然后尝试使用各种操作:max、mean、medium 来融合提取的全局特征中的代表帧,然后发现使用 max 操作可以更好地保留人类身份信息。最大操作定义为
T
=
Maxpooling
(
T
i
)
,
i
∈
1
,
2
,
…
,
N
.
T=\operatorname{Maxpooling}\left(T_{i}\right), i \in 1,2, \ldots, N .
T=Maxpooling(Ti),i∈1,2,…,N.
其中
T
i
T_{i}
Ti是 FEM 从原始步态序列中提取的全局特征,
T
T
T是通过 max 操作从
T
i
T_{i}
Ti中融合的最具代表性的时间特征。经过此操作,步态序列中最具代表性的时间特征可以很好地融合。
表1 特征提取模块的结构。 IN、OUT、KERNEL和PAD分别代表了CONV2D的输入输出通道、内核大小和填充。

2)细粒度特征提取:在以往的文献中,有研究者发现用局部特征来描述人体有突出的表现。然而,以往的研究都是分析浅层局部特征来描述人体,并且需要在不同的层特征中多次划分以提取细粒度特征,这将使网络结构更加复杂。因此,本文尝试从深层提取细粒度的特征,以简化网络结构并获得更好的结果。将提取的最具代表性的时间特征依次划分为 1、2、4 和 8 个块来学习细粒度信息,其中最具代表性的时间特征是高级特征。可以观察到,当使用 4 个块来学习细粒度特征时,它具有最好的性能。结果表明,当学习细粒度信息时,过度的阻塞并不能使细粒度信息学习得更充分,反而可能会忽略相邻部分之间的关系。还尝试使用更深的卷积层再次学习细粒度信息。但在大多数情况下,它的性能不如单个卷积层。结果有力地证明,在高级特征中使用局部思想时,不需要太深的网络结构来学习细粒度的信息。
具体来说,首先将最具代表性的帧划分为 4 个块。然后使用单个卷积层从每个块中学习细粒度信息。在此之后,使用全局池化和全连接层分别进一步整合细粒度特征和时空信息。 Global Pooling 的公式如下所示
P
=
Avgpooling
(
P
i
)
+
Maxpooling
(
P
i
)
,
i
∈
1
,
2
,
…
,
N
P=\operatorname{Avgpooling}\left(P_{i}\right)+\operatorname{Maxpooling}\left(P_{i}\right), i \in 1,2, \ldots, N
P=Avgpooling(Pi)+Maxpooling(Pi),i∈1,2,…,N
这两个池化操作都适用于 w 维度。通过这个操作,特征从包含 c、h 和 w 的三维数据变为包含 c 和 h 的二维数据。
步态识别主要使用特征匹配来识别目标。因此,不同目标之间的低相似度和同一目标之间的高相似度是决定识别准确率的重要因素。 hardtriplet loss在降低类间相似度和增加类内相似度方面有很好的表现。所以用这个损失作为约束来调整网络参数。硬三元组损失表示为
L
trip
=
max
(
max
max
(
d
i
+
)
−
min
(
d
i
−
)
,
0
)
d
i
+
=
∥
f
i
a
i
−
f
i
p
i
∥
2
2
d
i
−
=
∥
f
i
a
i
−
f
i
n
i
∥
2
2
\begin{gathered} L_{\text {trip }}=\max \left(\max \max \left(d_{i}^{+}\right)-\min \left(d_{i}^{-}\right), 0\right) \\ d_{i}^{+}=\left\|f_{i}^{a_{i}}-f_{i}^{p_{i}}\right\|_{2}^{2} \\ d_{i}^{-}=\left\|f_{i}^{a_{i}}-f_{i}^{n_{i}}\right\|_{2}^{2} \end{gathered}
Ltrip =max(maxmax(di+)−min(di−),0)di+=∥fiai−fipi∥22di−=∥fiai−fini∥22
其中
d
i
+
d_{i}^{+}
di+是表示正样本和锚点
(
a
i
\left(a_{i}\right.
(ai和
p
i
)
\left.p_{i}\right)
pi)的相异性的度量,
d
i
−
d_{i}^{-}
di−是表示负样本和锚点
(
a
i
\left(a_{i}\right.
(ai和
n
i
)
\left.n_{i}\right)
ni)的相异性的度量。使用欧几里得范数得到
d
i
+
d_{i}^{+}
di+和
d
i
−
d_{i}^{-}
di−的值。以
d
i
−
d_{i}^{-}
di−的最小值和
d
i
+
d_{i}^{+}
di+的最大值作为代表来计算损失,可以有效地降低类间相似度,增加类内相似度。
C. Adaptive Distance Alignment
在大多数情况下,Triplet loss 可以增加类内相似性并降低目标的类间相似性。然而,当遇到具有相似步行姿势的目标时,triplet loss 并不能保证他们之间的步态特征差异。所以尝试使用后处理的方法对提取的特征再次进行细化,使其更具判别力。引入自适应距离对齐技术来解决这个问题。首先,会在现实生活中发现大量未标记的步态数据。然后,使用经过训练的 SFE 模块从这些未标记的步态数据中提取时空特征。使用这些时空特征作为调整集 K G K_{G} KG。然后,计算 K G K_{G} KG中的特征与probe set和gallery set中的时空特征之间的距离,并选择一些与从 K G K_{G} KG中提取的时空特征相似的特征 F S F_{S} FS。最后,适应性的从 F S F_{S} FS中从整体(mean)、最大(maximum)和最适中(median)方面选择最合适的基准,并使用基准来细化提取的时空特征。图 2 显示了完整的特征细化过程。可以清楚地看到,经过ADA细化后,probe set和gallery set中特征的类内相似度和类间相异度有了很大的提高。接下来,将从准备和细化两个部分来介绍ADA。

图 2. 目标 I I I的步态序列和未标记的步态数据 Seqs 都输入到经过训练的 SFE 模块,可以看到从 I I I中提取的特征 F F F的类间差异和类内相似性很小,提取的时空特征来自未标记的被用作调整集 K G K_{G} KG,以细化从 I I I中提取的特征。经过此操作,特征F的类间相异度和类内相似度都在增加。
-
准备工作:这部分主要介绍了用自适应距离对齐来提炼提取的时空特征的准备工作。它可以分为三个部分。第一部分是在现实生活中发现大量未标记的步态数据 S e q s Seqs Seqs时应该遵守的。应确保该集合中未标记的数据应包含适当数量的目标,以确保集合的稳健性。如果目标数量少,则不够具有代表性,如果目标数量多,则会导致类似过拟合的问题。第二步是使用之前提出的 SFE 模块从集合 S e q s Seqs Seqs中提取时空特征。这一步可以看到这些目标的类间相似度和类内相似度应该有多少,并以此为基准来细化probe set和gallery set中的时空特征。最后,将这些从未标记数据中提取的时空特征作为调整集 K G K_{G} KG。 K G K_{G} KG的公式定义为
K G = f ( Seqs ) K_{G}=f(\text { Seqs }) KG=f( Seqs )
其中 S e q s Seqs Seqs是来自未标记步态数据的步态序列,其中包含适当数量的受试者。 f f f是上面提出的经过训练的时空特征提取模块。 K G K_{G} KG是用于细化图库集和探针集中时空特征的调整集。 -
Refinement:当从未标记的步态数据 S e q s Seqs Seqs中得到调整集 K G K_{G} KG时,首先计算 K G K_{G} KG中这些特征与probe set和gallery set中的时空特征之间的距离,并选择一些与提取的时空特征相似的特征来自 K G K_{G} KG。选择相似特征FS的公式定义为 P { d ( f , q i ) − d ( k , q i ) ) < 0 , k ∈ K G , f ∈ F S , F S ∈ K G } = 1 0 − t 1 . \left.P\left\{d\left(f, q_{i}\right)-d\left(k, q_{i}\right)\right)<0, k \in K_{G}, f \in F_{S}, F_{S} \in K_{G}\right\}=10^{-t 1} . P{d(f,qi)−d(k,qi))<0,k∈KG,f∈FS,FS∈KG}=10−t1.其中 q i q_{i} qi是从probe set和gallery set中目标 i i i的步态序列中提取的时空特征, f f f是 F S F_{S} FS中的时空特征。 k k k是 K G K_{G} KG中的时空特征。 d ( f , q i ) d\left(f, q_{i}\right) d(f,qi)表示 f f f和 q i q_{i} qi之间的距离。 d ( k , q i ) d\left(k, q_{i}\right) d(k,qi)表示 k k k和 q i q_{i} qi之间的距离。这个公式意味着 F S F_{S} FS中的 f f f与 q i q_{i} qi的距离小于 K G K_{G} KG中的 k k k与 q i q_{i} qi的距离的概率。它可以帮助找到一些特征 F S F_{S} FS,这些特征最类似于从 K G K_{G} KG中提取的时空特征。
当得到
F
S
F_{S}
FS时,会适应性地从整体(mean)、最大(maximum)和最适中(median)三个方面选择最合适的benchmark
θ
(
q
i
,
1
0
−
t
1
)
\theta\left(q_{i}, 10^{-t 1}\right)
θ(qi,10−t1),以达到最佳的细化效果。确定
θ
(
q
i
,
1
0
−
t
1
)
\theta\left(q_{i}, 10^{-t 1}\right)
θ(qi,10−t1)的公式定义为
a
d
a
p
=
(
max
(
∗
)
+
mean
(
∗
)
+
median
(
∗
)
)
/
3
,
θ
(
q
i
,
1
0
−
t
1
)
=
adap
(
d
(
f
,
q
i
)
)
,
f
∈
F
S
\begin{gathered} a d a p=(\max (*)+\operatorname{mean}(*)+\operatorname{median}(*)) / 3, \\ \theta\left(q_{i}, 10^{-t 1}\right)=\operatorname{adap}\left(d\left(f, q_{i}\right)\right), f \in F_{S} \end{gathered}
adap=(max(∗)+mean(∗)+median(∗))/3,θ(qi,10−t1)=adap(d(f,qi)),f∈FS
其中
F
S
F_{S}
FS是与probe set和gallery set中需要细化的特征相似的特征。 max、mean、median 分别代表最大值、平均值和中值。它可以确保
F
S
F_{S}
FS中所有类似的功能都被充分利用。 adpt 是一种自适应方法来选择合适的基准
θ
(
q
i
,
1
0
−
t
1
)
\theta\left(q_{i}, 10^{-t 1}\right)
θ(qi,10−t1)。
当计算出合适的
θ
(
q
i
,
1
0
−
t
1
)
\theta\left(q_{i}, 10^{-t 1}\right)
θ(qi,10−t1)时,可以调整之前提取的时空特征
q
i
q_{i}
qi。使用
θ
(
q
i
,
1
0
−
t
1
)
\theta\left(q_{i}, 10^{-t 1}\right)
θ(qi,10−t1)作为基准来细化时空特征,并使它们更具判别力。具体公式定义如下:
d
′
(
g
,
q
i
,
1
0
−
t
1
)
=
d
(
g
,
q
i
)
−
θ
(
q
i
,
1
0
−
t
1
)
d^{\prime}\left(g, q_{i}, 10^{-t 1}\right)=d\left(g, q_{i}\right)-\theta\left(q_{i}, 10^{-t 1}\right)
d′(g,qi,10−t1)=d(g,qi)−θ(qi,10−t1)
其中
d
(
g
,
q
i
)
d\left(g, q_{i}\right)
d(g,qi)是在确定步态序列
i
i
i属于哪个目标时,探针集中的目标
i
i
i与画廊集中的目标之间的原始距离,
θ
(
q
i
,
1
0
−
t
1
)
\theta\left(q_{i}, 10^{-t 1}\right)
θ(qi,10−t1)是时空的值需要细化目标
i
i
i的特征
q
i
q_{i}
qi,
d
′
(
g
,
q
i
,
1
0
−
t
1
)
d^{\prime}\left(g, q_{i}, 10^{-t 1}\right)
d′(g,qi,10−t1)是调整后的探针集中的目标
i
i
i与图库集中的目标之间的距离,用于判断目标的身份。但是,该公式仅对探针集中的特征进行调整,以修改特征匹配的最终距离。当想用一个调整集同时细化图库集和探针集中的目标的时空特征时,公式可以定义如下:
d
′
(
g
,
q
,
1
0
−
t
1
)
=
d
(
g
,
q
)
−
λ
g
∗
θ
(
g
,
1
0
−
t
1
)
−
λ
q
∗
θ
(
q
,
1
0
−
t
1
)
d^{\prime}\left(g, q, 10^{-t 1}\right)=d(g, q)-\lambda_{g} * \theta\left(g, 10^{-t 1}\right)-\lambda_{q} * \theta\left(q, 10^{-t 1}\right)
d′(g,q,10−t1)=d(g,q)−λg∗θ(g,10−t1)−λq∗θ(q,10−t1)
其中
θ
(
g
,
1
0
−
t
1
)
\theta\left(g, 10^{-t 1}\right)
θ(g,10−t1)是调整画廊集中目标时空特征的值,
θ
(
q
,
1
0
−
t
1
)
\theta\left(q, 10^{-t 1}\right)
θ(q,10−t1)是调整探针集中对象时空特征的值.
λ
g
\lambda_{g}
λg和
λ
q
\lambda_{q}
λq是确定细化程度的超参数。
参考文献
[43] X. Li, S. J. Maybank, S. Yan, D. Tao, and D. Xu, “Gait components and their application to gender recognition,” IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), vol. 38, no. 2, pp. 145–155, 2008.



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










