使用多跳时间转换在野外进行步态识别
paper题目:Gait Recognition in the Wild with Multi-hop Temporal Switch
该paper是杭电发表在MM 2022的工作
paper地址:链接
ABSTRACT
现有的步态识别研究以实验室场景为主。由于人们生活在现实世界的感官中,因此野外步态识别是一个更实际的问题,最近引起了多媒体和计算机视觉界的关注。目前在实验室基准测试中获得最先进性能的方法在最近提出的野外数据集上的准确性要差得多,因为这些方法很难模拟不受约束场景中步态序列的变化时间动态。因此,本文提出了一种新颖的多跳时间转换方法,以实现对真实场景中步态模式的有效时间建模。具体而言,我们设计了一种名为多跳时间转换网络 (MTSGait) 的新型步态识别网络,以同时学习空间特征和多尺度时间特征。与使用 3D 卷积进行时间建模的现有方法不同,我们的 MTSGait 通过 2D 卷积对步态序列的时间动态进行建模。通过这种方式,它以更少的模型参数实现了高效率,并且与基于 3D 卷积的模型相比降低了优化难度。基于二维卷积核的具体设计,我们的方法可以消除相邻帧之间特征的错位。此外,还提出了一种新的采样策略,即非循环连续采样,使模型学习到更鲁棒的时间特征。最后,与最先进的方法相比,所提出的方法在两个公共步态野外数据集(即 GREW 和 Gait3D)上实现了卓越的性能。
1 INTRODUCTION
步态是反映行人行走方式的一种极具潜力的生物学特征。由于运动和体型的差异,目标行人可以通过步态进行唯一识别[22, 31]。与人脸、指纹不同,步态具有可远程访问、非接触、难以伪装等特点,在社会安全方面具有独特的潜力。然而,由于现实世界场景中存在各种不确定因素,例如遮挡、不同的视角、任意行走方式等,步态识别仍然是一项非常具有挑战性的任务 [48, 50]。
通常,根据输入类型,步态识别可分为两类:基于模型的方法和无模型的方法。基于模型的方法通常将 2D/3D 关键点作为输入。然而,由于丢失了许多有用的步态信息,如身体形状、外观等,基于模型的方法在性能上往往不如无模型方法[48]。无模型方法主要使用轮廓作为步态表示。最近,基于深度学习的方法在 CASIA-B [42] 和 OU-MVLP [28] 等广泛采用的步态识别基准上实现了最先进的性能。例如,GaitSet [2] 将步态序列视为无序集合,通过最大池化提取时空信息,达到了当时的最佳性能。但是时间信息仍然丢失。 GaitGL [18] 采用 3D 卷积来提取时空特征,并设计全局和局部分支以收集更多有用的步态知识,从而显着提高步态识别的性能。然而,由于遮挡、任意视点和其他具有挑战性的因素,3D 卷积存在特征未对齐的问题,尤其是在真实场景中,如图 1 所示。

图 1:(a) 通过在相邻特征图上滑动时空块对基于 3D 卷积的方法进行时间建模。 (b) 我们通过在帧之间切换通道的时间建模。 T表示时间,h、w、c分别表示步态特征的高度、宽度和通道维度。 (最好以彩色观看。)
尽管这些方法在实验室数据集上取得了出色的性能,但它们在 GREW [50] 和 Gait3D [48] 等野外数据集上效果不佳。我们仔细分析了这种现象,发现野外步态存在很多具有挑战性的因素,比如遮挡、视角多变、行走方式随意等等。现有的基于时间的方法,如 GaitGL [18] 和 CSTL [9] 没有充分考虑上述挑战,因此他们在真实世界的步态数据集上获得了较差的结果。特别地,现有的用于时间建模的3D卷积方法仍然存在以下三个缺点:首先,在3D卷积的操作中存在外观错位的问题。换句话说,不同帧的相同位置可能不同。如图 1 所示,由于现实世界场景中 3D 视角和不规则行走方式的挑战,前一帧中手的位置可能会在下一帧中变为腿部。其次,3D卷积参数量大,优化难度特别大。第三,3D卷积严重依赖预训练模型,据我们所知,在步态识别领域还没有对应的3D预训练模型。
为了解决上述缺点并更好地模拟野外步态识别的时间信息,本文提出了一种多跳时间变换方法。如图 1 所示,为了避免基于 3D 卷积的方法中的特征未对齐问题,我们采用帧之间的通道变换来实现时间建模。实验结果和可视化证明我们的方法确实使模型更加关注运动信息,例如脚部运动,此外,我们提出了一种新颖的步态识别网络,即多跳时间切换网络(MTSGait)。 MTSGait 由两个分支组成:空间分支和多跳时间变换分支。空间分支可以减少变换操作对外观特征的破坏。多跳时间开关分支允许模型学习多尺度时间信息。需要指出的是,我们方法中的所有操作都依赖于 2D 卷积。也就是说,我们的方法不存在大规模模型参数和训练困难的问题。此外,我们发现先前将步态假设为循环运动是有问题的,因此我们提出了一种新的步态数据采样策略,即非循环连续采样,它可以使模型学习更鲁棒的时间特征。
总之,本文的贡献如下:
- 我们提出了一种新颖的步态识别网络,即 MTSGait。该网络由空间分支和多跳时间切换变换组成,保证了模型可以同时学习空间和多尺度时间信息。
- 我们的MTSGait 通过2D 卷积实现时间建模,没有像基于3D 卷积的方法那样存在大规模模型参数和训练困难的问题。
- 为了更好地提取步态识别的时间信息,尤其是在真实场景中,我们提出了一种新的采样策略,即非循环连续采样,它可以改进模型以学习更稳健的时间特征。
- 与最先进的方法相比,我们的方法在两个公共步态野外数据集(即 GREW 和 Gait3D)上实现了卓越的性能。
2 RELATED WORK
2.1 Gait Recognition
目前,步态识别方法主要有两大类:基于模型的方法和无模型的方法[24, 31]。基于模型的方法侧重于人体的结构建模,例如2D/3D人体关键点等。早期的方法主要属于基于模型的方法。例如,Yam 等人 [34] 使用耦合振荡器和人体运动的生物力学来模拟行走和破坏模式。 Yamauchi 等人 [35] 提出了第一种使用 RGB 帧中的 3D 关键点进行步行人体识别的方法。 Ariyanto 和 Nixon [1] 应用了一个复杂的多摄像头系统来构建一个基于 3D 体素的数据集,并提出了一个在每个关节处具有 3D 自由度的铰接式圆柱体结构模型来模拟人类小腿。最近,也有一些基于模型的步态识别方法。 Liao et al [16] 基于三维关键点定义关节角度、肢体长度和关节运动,并使用三个定义的信息结合姿势特征作为步态表示。 Teepe 等人 [29] 将 2D 骨架建模为图,并采用图卷积网络,即 ResGCN [26],通过对比损失来学习特征。 Li等人[15]结合人体的2D和3D关键点信息作为步态表示,并使用卷积神经网络(CNNs)[13]提取步态特征。
基于模型的方法对服装和相机视角的变化具有鲁棒性。然而,由于丢失了很多有用的步态信息,如体形信息,基于模型的方法在性能上往往不如无模型方法。无模型方法主要使用轮廓作为步态表示。早期,Han 等[4]提出在时间维度上压缩序列的轮廓,从而获得步态能量图像(GEI)。最近,由于深度学习在多媒体和计算机视觉任务上的成功 [5、20、21、27、33、36-40],基于深度学习的方法也主导了步态识别的性能。例如,Shiraga 等人 [25] 和 Wu 等人 [32] 提出通过 CNN 从 GEI 中学习步态特征,并且明显优于以前的方法。 Zhang 等人 [43] 开发了一种基于连体神经网络的步态识别框架,可以自动从 GEI 中提取稳健且具有辨别力的步态特征。最近的方法开始直接从轮廓序列中提取步态特征。例如,Chao 等人 [2] 将步态序列视为一个集合,而不考虑时间信息,并使用 CNN 提取帧级和集合级特征。 Hou 等人 [8] 设计了一个紧凑的块,将步态特征的维数从 15,872 减少到 256。Fan 等人 [3] 提出了一种名为 GaitPart 的新型网络,用于水平分割步态轮廓并从每个部分提取详细特征. Huang 等人 [10] 提出了一种 3DLocalCNN 网络,可以实现更精细的人体部位的定位和特征提取。 Lin 等人 [18] 使用 3D 卷积同时提取空间和时间信息,并提出了一个 GLConv 模块来聚合全局和局部特征。 Zheng 等人 [49] 使用 Transferable Neighborhood Discovery 框架对无监督跨域步态识别进行了首次探索。尽管这些方法大大提高了步态识别的准确性,但它们仅在实验室环境,即受限环境中进行。人们生活在现实世界的感觉中,即不受约束的环境中,在野外场景中促进步态识别非常重要。
幸运的是,一些研究人员已经开始关注这一领域,并在真实场景中制作了大规模的步态基准,推动了步态识别从实验研究走向实际应用。 Zhu 等人 [50] 首先建立了一个名为 GREW 的野外最大步态基准。它包含来自大型公共区域 882 个摄像头的 26K 对象和 128K 具有丰富属性的序列,这使其成为第一个用于无约束步态识别的数据集。他们还进行了广泛的步态识别实验,包括代表性方法、属性分析等。结果表明,野外步态识别对于当前的 SOTA 方法来说是一项非常具有挑战性的任务。 Zheng 等人[48] 指出,人类生活和行走在不受约束的 3D 空间中,因此将 3D 人体投影到 2D 平面上会丢弃很多关键信息,如视角、形状等。要实现 3D 步态识别在真实场景中,他们构建了第一个大规模 3D 步态识别数据集,名为 Gait3D,它提供了从无约束环境中收集的步态的 3D 人体mesh、2D/3D 关键点和 2D 剪影。他们还提出了一种名为 SMPLGait 的新型 3D 步态识别框架,以探索用于步态识别的 3D 人体mesh。基于 Gait3D 数据集,他们进行了大量实验,发现现有的 SOTA 方法通常在 Gait3D 上失败,尽管在实验室数据集上表现出色,例如 CASIA-B [42] 和 OU-LP [11] .以上两个基准对真实场景中的步态识别起到了很大的促进作用。为促进步态识别的应用,本文主要针对野外步态识别任务进行研究。
2.2 Temporal Modeling
早期的研究人员人工构建了用于步态识别的时间信息。例如,Urtasun 和 Fua [30] 使用关节骨架的 3D 时间运动模型进行步态分析。 Zhao 等人 [47] 提出了一种局部优化算法来跟踪步态识别的 3D 运动。最近的步态时间建模方法可以分为四类:基于集合的、基于 LSTM 的、基于 1DCNN 的和基于 3DCNN 的。 GaitSet [2] 和 GLN [8] 将步态序列视为无序集,并通过时间池提取时空信息。但是,这会丢失很多有用的时间特征。 Zhang 等人 [46] 和 Huang 等人 [45] 应用 LSTM 来实现短-长时间建模。 GaitPart [3] 和 CSTL [9] 采用一维卷积来模拟短期和长期时间特征。 MT3D [17] 和 GaitGL [18] 利用 3D 卷积直接对时空特征进行建模,但这些方法通常难以训练且计算内存昂贵。 Lin [19] 提出时间建模可以通过在时间上滑动通道信息来实现。然而,我们发现直接传输通道信息可能会损害空间特征,从而降低步态识别的性能。在本文中,我们构建了一个新颖的步态识别网络,即 MTSGait,它包含空间分支和多跳时间变换分支。该结构保证模型可以同时学习空间和多尺度时间知识。此外,所提出的 MTSGait 网络完全基于 2D 卷积,没有大规模模型参数和训练困难的问题。
3 THE PROPOSED METHOD
在本节中,我们首先介绍所提出框架的概述。然后,我们描述了我们方法的关键组成部分,包括空间和时间特征提取器和多跳时间变换 (MTS)。接下来,我们讨论现有的步态数据采样策略并提出一种新的采样方法。最后,介绍了训练和推理的细节。
3.1 Overview
所提出的步态识别框架的概述如图 2 所示。首先,剪影的采样序列被送入 2D 卷积以提取浅层特征。我们将
X
i
=
{
x
i
}
i
=
1
N
X_i=\left\{\mathrm{x}_i\right\}_{i=1}^N
Xi={xi}i=1N作为输入序列,其中
x
i
∈
R
1
×
H
×
W
,
N
x_i \in \mathbb{R}^{1 \times H \times W}, N
xi∈R1×H×W,N是采样序列的长度,
H
H
H和
W
W
W是步态轮廓的高度和宽度。该过程可以表述为:
F
i
=
ReLU
(
f
b
a
×
a
(
X
i
)
)
\mathrm{F}_i=\operatorname{ReLU}\left(f_b^{a \times a}\left(X_i\right)\right)
Fi=ReLU(fba×a(Xi))
其中
ReLU
(
⋅
)
\operatorname{ReLU}(\cdot)
ReLU(⋅)是 LeakyReLU 激活函数,
f
b
a
×
a
(
⋅
)
f_b^{a \times a}(\cdot)
fba×a(⋅)是具有内核大小
a
a
a和步幅
b
b
b的二维卷积旨在从每个步态轮廓中提取帧级特征,
F
i
∈
R
N
×
c
×
h
×
w
\mathrm{F}_i \in \mathbb{R}^{N \times c \times h \times w}
Fi∈RN×c×h×w是
X
i
\mathrm{X}_{i}
Xi的特征图,
c
c
c是通道数,
h
h
h和
w
w
w是特征图的高度和宽度。
接下来,空间和时间特征提取器旨在整合空间和时间信息。然后,我们引入一个特征映射头来进一步映射特征。最后,我们使用三元组损失和交叉熵损失来训练模型。我们将详细介绍以上模块。

图 2:提出的 MTSGait 框架概述。 (最好以彩色观看。)
3.2 Spatial and Temporal Feature Extractor
如图 2 所示,时空特征提取器由空间分支、多跳时间变换 (MTS) 分支、LeakyReLU 和最大池化组成。 MTS分支也可以分为不同的时间尺度分支,可以帮助模型从步态序列中学习到更多的时间信息。由于我们的时间分支可能会损害空间特征,因此有必要添加空间分支。具体来说,空间分支是通过2D卷积实现的。该过程可以表述为:
G
i
=
MTS
(
F
i
)
+
f
b
a
×
a
(
F
i
)
\mathrm{G}_i=\operatorname{MTS}\left(\mathrm{F}_i\right)+f_b^{a \times a}\left(\mathrm{~F}_i\right)
Gi=MTS(Fi)+fba×a( Fi)
其中
M
T
S
(
⋅
)
M T S(\cdot)
MTS(⋅)为 MTS 分支的操作,
G
i
∈
R
N
×
c
′
×
h
′
×
w
′
\mathrm{G}_i \in \mathbb{R}^{N \times c^{\prime} \times h^{\prime} \times w^{\prime}}
Gi∈RN×c′×h′×w′是包含空间和多尺度时间信息的特征图。
3.3 Multi-hop Temporal Switch (MTS)
最近,已经提出了许多时间建模方法,例如 MT3D [17] 和 GaitGL [18],通过使用 3D 卷积来提取时间信息。然而,由于现实场景中3D视角和不规则行走方式的挑战,手的位置可能会在下一帧变成腿。 3D 卷积通过在相邻特征图上滑动时空块来工作。这种工作机制使其在时间层面的特征严重错位,尤其是在现实世界中,如图1所示。此外,3D卷积具有大量参数,因此优化特别困难。即训练3D卷积严重依赖预训练模型,据我们所知,在步态识别领域还没有对应的3D预训练模型。
为了解决上述问题,我们引入了MTS分支来进行多尺度时间建模。基于 2D 卷积核特别针对不同模式的假设 [44],我们在帧之间变换通道以实现时间建模。假设将2D卷积的权重拆分为
W
=
(
ω
1
,
ω
2
,
ω
3
)
W=\left(\omega_1, \omega_2, \omega_3\right)
W=(ω1,ω2,ω3)三部分,帧
t
t
t的输入特征图可以在通道维度上拆分为
F
t
=
(
F
t
1
,
F
t
2
,
F
t
3
)
F_t=\left(F_t^1, F_t^2, F_t^3\right)
Ft=(Ft1,Ft2,Ft3).二维卷积在帧
T
T
T上的操作可以写成:
f
b
a
×
a
(
F
t
)
=
ω
1
F
t
1
+
ω
2
F
t
2
+
ω
3
F
t
3
,
f_b^{a \times a}\left(\mathrm{~F}_t\right)=\omega_1 F_t^1+\omega_2 F_t^2+\omega_3 F_t^3,
fba×a( Ft)=ω1Ft1+ω2Ft2+ω3Ft3,
现在,我们变换部分通道,即,
F
t
1
F_t^1
Ft1替换为
F
t
−
1
1
F_{t-1}^1
Ft−11,
F
t
3
F_t^3
Ft3替换为
F
t
+
1
3
F_{t+1}^3
Ft+13,
F
t
2
F_t^2
Ft2保持不变。该操作可以表示如下:
f
b
a
×
a
(
F
t
−
1
,
F
t
,
F
t
+
1
)
=
ω
1
F
t
−
1
1
+
ω
2
F
t
2
+
ω
3
F
t
+
1
3
,
f_b^{a \times a}\left(\mathrm{~F}_{t-1}, \mathrm{~F}_t, \mathrm{~F}_{t+1}\right)=\omega_1 F_{t-1}^1+\omega_2 F_t^2+\omega_3 F_{t+1}^3,
fba×a( Ft−1, Ft, Ft+1)=ω1Ft−11+ω2Ft2+ω3Ft+13,
这样,二维卷积运算就可以整合上一帧、当前帧和下一帧的信息。我们还可以进行更长时间跨度的版本。该过程可以表述为:
f
b
a
×
a
(
F
t
−
j
,
F
t
,
F
t
+
j
)
=
ω
1
F
t
−
j
1
+
ω
2
F
t
2
+
ω
3
F
t
+
j
3
,
f_b^{a \times a}\left(\mathrm{~F}_{t-j}, \mathrm{~F}_t, \mathrm{~F}_{t+j}\right)=\omega_1 F_{t-j}^1+\omega_2 F_t^2+\omega_3 F_{t+j}^3,
fba×a( Ft−j, Ft, Ft+j)=ω1Ft−j1+ω2Ft2+ω3Ft+j3,
最后,我们结合多跳时间变换特性,实现了多尺度时间建模。该操作可以表示如下:
MTS
(
F
i
)
=
∑
j
=
1
S
f
b
a
×
a
(
F
i
−
j
,
F
i
,
F
i
+
j
)
,
j
=
1
,
2
,
…
,
S
,
\operatorname{MTS}\left(\mathrm{F}_i\right)=\sum_{j=1}^S f_b^{a \times a}\left(\mathrm{~F}_{i-j}, \mathrm{~F}_i, \mathrm{~F}_{i+j}\right), j=1,2, \ldots, S,
MTS(Fi)=j=1∑Sfba×a( Fi−j, Fi, Fi+j),j=1,2,…,S,
其中
S
S
S是时间跨度,
F
i
F_i
Fi是MTS模块的输入特征图。在我们的实现中,我们将特征图在通道维度上划分为
m
m
m部分,第一部分和最后一部分的特征以单向或双向方式切换,如图 3 所示。
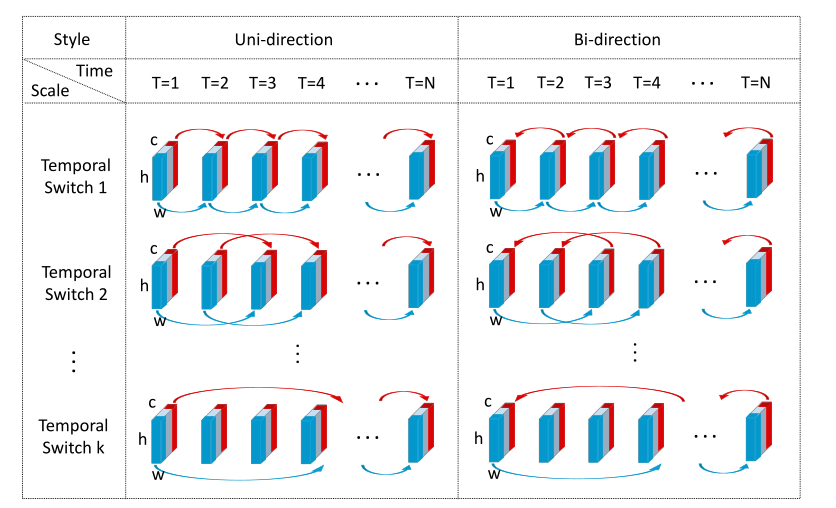
图 3:单向、双向和多跳临时变换操作的图示。 (最好以彩色观看。)
3.4 Feature Mapping Head
略
3.5 Gait Sampling Strategy
现有的基于视频的行人重识别和基于序列的步态识别方法采样固定长度的序列作为输入。 Chao等人[2]提出了将步态序列视为一个集合的思想,从而丢弃帧之间的顺序,从一个步态序列中随机采样 N N N帧。最近的研究提倡探索步态的时间信息。Hou et al [7] 以固定长度的步长有序采样帧,即均匀采样。基于步态是周期性运动的假设,Lin等[18]和Fan等[3]提出了循环连续采样策略。具体来说,在一个步态序列中连续固定长度的样本帧,当序列长度短于样本长度时,循环遍历该序列,直至达到样本长度。
然而,我们发现步态序列的开始和结束之间往往存在很大差异,这对模型来说是一个很大的噪声。特别是当数据集有大量长度小于采样长度的步态序列时,这种噪声对于模型学习时间知识是致命的。基于以上分析,我们设计了一种新的采样策略,即非循环连续采样。我们将
X
=
{
x
1
,
x
2
,
…
,
x
L
}
X=\left\{\mathrm{x}_1, x_2, \ldots, x_L\right\}
X={x1,x2,…,xL}作为输入序列,其中
x
i
∈
R
H
×
W
\mathrm{x}_i \in \mathbb{R}^{H \times W}
xi∈RH×W是第
i
i
i个二进制帧,
L
L
L是序列的长度,
H
H
H和
W
W
W是轮廓图像的高度和宽度。非循环连续采样的过程可以表述为:
X
N
=
{
[
x
(
t
+
1
)
,
x
(
t
+
2
)
,
…
,
x
(
t
+
N
)
]
,
L
>
=
N
,
Sort
(
[
x
1
,
x
2
,
…
,
x
L
,
x
1
,
…
,
x
(
N
−
L
)
]
)
,
L
<
N
,
=
{
[
x
(
t
+
1
)
,
x
(
t
+
2
)
,
…
,
x
(
t
+
N
)
]
,
L
>
=
N
,
[
x
1
,
x
1
,
…
,
x
(
N
−
L
)
,
x
(
N
−
L
)
,
x
(
N
−
L
+
1
)
,
…
,
x
L
]
,
L
<
N
,
\begin{aligned} X_N & = \begin{cases}{\left[x_{(t+1)}, x_{(t+2)}, \ldots, x_{(t+N)}\right],} & L > = N, \\ \operatorname{Sort}\left(\left[x_1, x_2, \ldots, x_L, x_1, \ldots, x_{(N-L)}\right]\right), & L < N,\end{cases} \\ & = \begin{cases}{\left[x_{(t+1)}, x_{(t+2)}, \ldots, x_{(t+N)}\right],} & L > =N, \\ {\left[x_1, x_1, \ldots, x_{(N-L)}, x_{(N-L)}, x_{(N-L+1)}, \ldots, x_L\right],} & L < N,\end{cases} \end{aligned}
XN={[x(t+1),x(t+2),…,x(t+N)],Sort([x1,x2,…,xL,x1,…,x(N−L)]),L>=N,L<N,={[x(t+1),x(t+2),…,x(t+N)],[x1,x1,…,x(N−L),x(N−L),x(N−L+1),…,xL],L>=N,L<N,
其中
N
N
N是采样长度,
t
∈
[
0
,
L
−
N
]
t \in[0, L-N]
t∈[0,L−N]是随机采样起始索引,
X
N
X_N
XN是采样序列。 4.5 节中的实验验证了所提出的非循环连续采样策略可以使模型学习到更鲁棒的时间信息。
Results
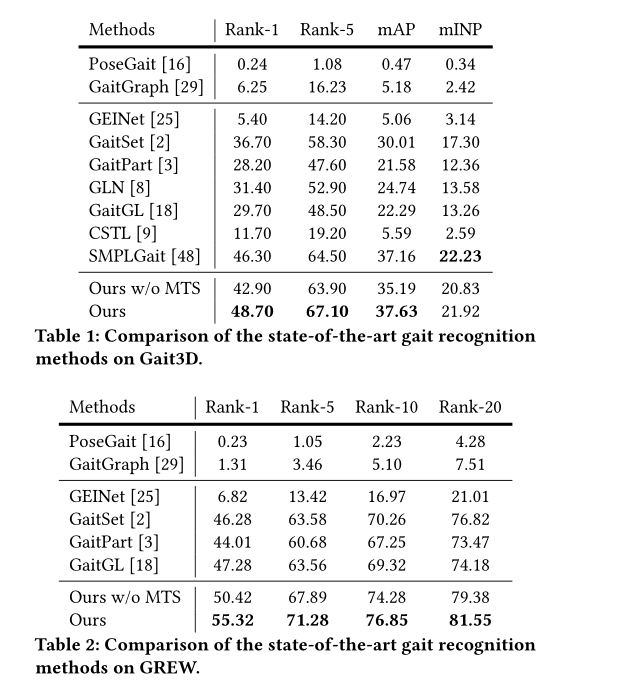








 文章提出了一种新的步态识别方法,称为MTSGait,它利用多跳时间转换来处理野外环境中的步态识别挑战。MTSGait网络包括空间分支和多跳时间变换分支,通过2D卷积实现时间建模,解决了3D卷积中的特征对齐问题和优化难题。此外,文章还引入了非循环连续采样策略,以增强模型对时间特征的学习。在GREW和Gait3D两个野外数据集上,MTSGait展示了优越的性能。
文章提出了一种新的步态识别方法,称为MTSGait,它利用多跳时间转换来处理野外环境中的步态识别挑战。MTSGait网络包括空间分支和多跳时间变换分支,通过2D卷积实现时间建模,解决了3D卷积中的特征对齐问题和优化难题。此外,文章还引入了非循环连续采样策略,以增强模型对时间特征的学习。在GREW和Gait3D两个野外数据集上,MTSGait展示了优越的性能。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










