(CVPR-2024)FreeU：扩散 U-Net 中的免费午餐

FreeU：扩散 U-Net 中的免费午餐

Paper Title：FreeU: Free Lunch in Diffusion U-Net

Paper是NTU S-Lab发表在CVPR 2024的工作

Paper地址

代码地址

图 1. FreeU 在无需付出任何代价的情况下大幅提高了扩散模型样本质量：无需训练、无需引入额外的可学习参数、无需增加内存或采样时间。

Abstract

在本文中，我们揭示了扩散 U-Net 尚未开发的潜力，它就像一顿“免费午餐”，可以大幅提高生成质量。我们首先研究了 U-Net 架构对去噪过程的关键贡献，并确定其主干主要用于去噪，而其跳跃连接主要将高频特征引入解码器模块，从而导致可能忽略主干网络固有的关键功能。利用这一发现，我们提出了一种简单而有效的方法，称为“FreeU”，它无需额外的训练或微调即可提高生成质量。我们的主要见解是战略性地重新加权来自 U-Net 的跳跃连接和主干特征图的贡献，以利用 U-Net 架构的两个组件的优势。图像和视频生成任务的良好结果表明，我们的 FreeU 可以轻松集成到现有的扩散模型中，例如稳定扩散、DreamBooth 和 ControlNet，只需几行代码即可提高生成质量。您只需在推理过程中调整两个缩放因子。

1. Introduction

扩散概率模型是一类前沿的生成模型，已引起广泛关注，尤其是在与计算机视觉相关的任务中 [7、8、11、18、33、41、45、46、49]。这些扩散模型由两个关键过程组成：扩散过程和去噪过程。在扩散过程中，高斯噪声逐渐添加到输入数据中，最终将其破坏为近似纯高斯噪声。在去噪过程中，通过学习到的一系列逆扩散操作将原始输入数据从噪声状态中恢复过来。通常，使用 U-Net 在每个去噪步骤中迭代预测要去除的噪声。现有研究 [3、47、58、65] 主要侧重于将预训练的扩散 U-Net 用于下游应用，而扩散 U-Net 的内部属性仍未得到充分探索。

在本文中，我们深入研究了扩散 U-Net 的去噪过程。为了进行全面分析，我们的第一个目标是探索去噪过程中图像如何从噪声中生成的机制。为了了解发生了什么，我们在傅里叶域内进行了调查，重点关注去噪过程中的生成演化。我们细致的分析揭示了低频分量的微妙调制，其变化率平缓。相反，高频分量在整个去噪过程中表现出更明显的动态。从根本上说，低频分量赋予图像其基础结构和颜色属性。迭代去噪过程中的过度调整可能会破坏图像的内在语义完整性。高频分量代表边缘和纹理等细节，受噪声的影响更大。因此，去噪过程的目标是在确保保留关键细节的同时减少这种噪声。

基于这一基础理解，我们将分析范围扩展到扩散 U-Net 如何实现去噪过程，从而确定 U-Net 架构在扩散框架内的具体贡献。从结构上讲，U-Net 架构包括一个主骨干网络，包含一个编码器和一个解码器，以及连接编码器和解码器之间信息传输的跳跃连接，如图 2 所示。我们的研究表明，U-Net 的主骨干主要有助于去噪。相反，观察到跳跃连接将高频特征引入解码器模块。这些连接传播高频信息，使 U-Net 更容易在训练期间恢复输入数据。然而，这种传播的一个意想不到的后果是，在推理过程中，骨干固有的去噪能力可能会减弱。这可能导致生成质量下降，例如图像细节异常，如图 1 所示。

图 2. FreeU 框架。（a）U-Net 跳跃特征和主干特征。在 U-Net 中，跳跃特征和主干特征在每个解码阶段连接在一起。我们在连接过程中应用 FreeU 操作。（b）FreeU 操作。采用两个调制因子（b 和 s）来平衡主干和跳跃连接的特征贡献。

在这些发现的背景下，我们继续推进一项新策略的引入，即“FreeU”，该策略有可能提高样本质量，而无需额外训练或微调的计算开销。具体来说，在推理过程中，我们实例化两个专门的调制因子，旨在平衡 U-Net 架构主干和跳过连接的特征贡献。第一个称为主干特征因子，旨在放大主干的特征图，从而增强去噪过程。然而，我们发现，虽然加入主干特征缩放因子可以带来显着的改进，但有时会导致纹理过度平滑。为了缓解这个问题，我们引入了第二个因子，即跳过特征缩放因子，旨在缓解纹理过度平滑的问题。

我们的 FreeU 方法与现有扩散模型集成时表现出无缝的适应性。我们对我们的方法进行了全面的实验评估，采用 Stable Diffusion [43, 46]、ModelScope [37]、Dreambooth [47]、ReVersion [23]、Rerender [61]、ScaleCrafter [16]、Animatediff [14] 和 ControlNet [65] 作为基准比较的基础模型。通过在推理阶段使用 FreeU，这些模型表明生成样本的质量有明显的提高，如图 1 所示。我们的贡献总结如下：

• 我们研究了傅里叶域中的去噪过程，发现低频分量逐渐变化，而高频分量表现出更显著的变化。
• 我们对扩散 U-Net 的潜力进行了开创性的探索，强调其主干主要用于去噪，而其跳跃连接将高频特征引入解码器。这种新颖的视角为社区提供了新的研究机会。
• 我们引入了一种简单而有效的方法，称为“FreeU”，它通过利用 UNet 架构的两个组件的优势来增强 U-Net 的去噪能力。
• 我们在各种扩散模型上对我们的方法进行了实证评估，证明了样本质量的显着改善和 FreeU 的有效性，而无需额外成本。

2. Methodology

2.1. Preliminaries

---

从扩散模型生成样本的过程始于从高斯噪声分布中采样，并随后依据逆扩散过程 $p_{\theta }\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t\right)$ 进行。这导致了一个轨迹序列 ${\mathbf{x}}_T$, ${\mathbf{x}}_{T-1},\dots ,{\mathbf{x}}_0$，最终生成样本 ${\mathbf{x}}_0$。关键在于采样过程依赖于去噪模型 ${ϵ}_{\theta }$ 来消除噪声。去噪模型的优化目标如下所示：
$${\mathcal{L}}_{DM}={\mathbb{E}}_{\mathbf{x},ϵ\sim \mathcal{N}(0,1),t}\left[{\Vert ϵ-{ϵ}_{\theta }\left({\mathbf{x}}_t,t\right)\Vert }_2^2\right](1)$$

在大多数实现中，去噪模型使用时间条件的 U-Net 结构实现。因此，其去噪能力在确定生成数据质量方面起着至关重要的作用。

2.2. How to Generate Images from Noise During Denoising Process?

---

图3. 去噪过程可视化：上行显示去噪过程生成的图像，下两行显示逆傅里叶变换后的低频和高频分量，低频分量变化较慢，而高频分量在去噪过程中变化较明显。

图 4. 去噪过程中傅里叶的相对对数振幅。在每个去噪步骤$t$中，我们可视化恢复数据$x_t$的傅里叶的相对对数振幅。我们观察到$x_t$的高频分量在去噪过程中急剧下降。

为了更好地理解去噪过程，我们在傅里叶域内进行了研究，以透视扩散模型的生成过程。如图 3 所示，最上行提供了渐进式去噪过程，展示了连续迭代中生成的图像。接下来的两行展示了逆傅里叶变换后相关的低频和高频空间域信息，与每个相应的步骤对齐。

从图3可以看出，低频分量的调制逐渐加强，变化速度较平缓，而高频分量的变化则在整个去噪过程中较为明显，图4进一步印证了这一结论，直观的解释是：1）低频分量本身就体现了图像的整体结构和特征，包括整体的布局、平滑的色彩，是图像本质和表象的基本全局要素，去噪过程中，低频分量的快速改变一般是不合理的，如果对这些分量进行剧烈的改变，可能会从根本上重塑图像的本质，这通常与去噪的目的不相符。2）相反，高频分量中包含了图像中快速变化的部分，比如边缘、纹理等，这些精细的细节对噪声特别敏感，在噪声引入图像后，往往表现为随机的高频信息，因此，去噪过程需要在去除噪声的同时，保留图像中不可或缺的精细细节。

2.3. How does Diffusion U-Net Perform Denoising?

---

基于对整个去噪过程的这一基本理解，我们扩展了研究范围，以描述 U-Net 架构在去噪过程中的具体贡献，探索去噪网络的内部属性。如图 2 所示，U-Net 架构由一个主干网络以及促进编码器和解码器之间信息传输的跳跃连接组成。

为了评估主干和横向跳跃连接在去噪过程中的作用，我们进行了一项受控实验，其中我们引入了两个乘性缩放因子（表示为 b 和 s），分别在连接主干和跳跃连接之前调节由主干和跳跃连接生成的特征图。如图 5 所示，很明显，提高主干的缩放因子 b 可以明显提高生成图像的质量。相反，缩放因子 s 的变化（调节横向跳跃连接的影响）似乎对生成图像的质量影响有限。

图 5. 主干和跳过连接缩放因子（b 和 s）的影响。增加主干缩放因子 b 可显著提高图像质量，而直接缩放跳过特征中的 s 对图像合成质量的影响有限。

U-Net 的主干。基于这些观察，我们随后探究了当与主干特征图相关的缩放因子 b 增加时图像生成质量增强的根本机制。分析表明，这种质量提升从根本上与 U-Net 架构主干赋予的增强去噪能力有关。如图 6 所示，b 的相应增加相应地抑制了扩散模型生成的图像中的高频成分。因此，在图 5 中，当 b = 0.6 时，生成的图像会出现大量噪声，从而对图像质量产生不利影响。相反，当 b = 1.4 时，可以生成非常清晰的图像。
这表明 U-Net 主干网络的主要作用是滤除高频噪声。增强主干特征可有效提升 U-Net 架构的去噪能力，从而有助于在保真度和细节保留方面获得卓越的输出。

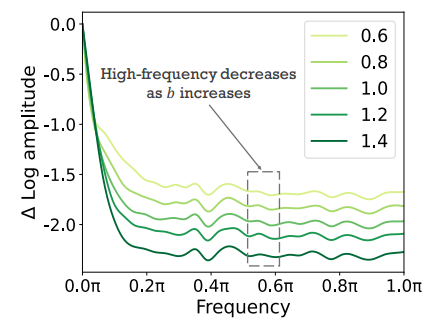
图 6. 傅里叶相对对数振幅随主干缩放因子 b 变化而变化。b 的增加相应地导致扩散模型生成的图像中高频分量的抑制。

U-Net 的跳跃连接。相反，跳跃连接用于将特征从编码器块的较早层直接转发到解码器。有趣的是，如图 7 所示，这些特征主要构成高频信息。基于这一观察，我们推测，在 U-Net 架构的训练过程中，这些高频特征的存在可能会无意中加速向噪声预测的收敛，优化目标为公式(1)，从而更容易重建输入数据。反过来，这种现象可能会导致主干固有去噪能力的功效意外减弱。
然而，与目标是重建输入数据的训练过程不同，推理过程旨在从高斯噪声中生成数据。扩散模型的生成能力体现在其去噪能力中。
因此，在推理过程中，必须增强 U-Net 的去噪能力，以确保高质量的数据生成。

图 7.骨干、跳跃和其融合特征图的傅里叶相对对数振幅。跳跃特征包含大量高频信息。

2.4. Free Lunch in Diffusion U-Net

---

图 8. 平均特征图的可视化：此可视化显示沿主干特征的通道维度的平均特征图。

图 9. 使用不同的主干缩放操作生成的图像：（a）无主干缩放，（b）缩放所有通道，（c）缩放半通道。

图 10. 未使用跳过缩放 (w/o s) 和使用跳过缩放 (w/ s) 时生成的 FreeU 图像。

基于上述发现，我们进一步推出了一种简单而有效的方法，称为“FreeU”，该方法通过利用 U-Net 架构的两个组件的优势，有效地增强了 U-Net 架构的去噪能力。它无需额外的训练或微调即可大幅提高生成质量。

骨干因子。为了增强 U-Net 的去噪能力，我们引入了一种称为结构感知缩放的新方法，该方法可以为每个样本动态调整骨干特征的缩放。与对所有样本或同一通道内的位置应用固定缩放因子不同，我们的方法根据样本特征的具体特性自适应地调整缩放因子。我们首先计算通道维度上的平均特征图：
$${\overline{\mathbf{x}}}_l=\frac{1}{C}\sum _{i=1}^C{\mathbf{x}}_{l,i}$$
其中，${\mathbf{x}}_{l,i}$ 表示 U-Net 解码器的第 $l$ 块中骨干特征图 $x_l$ 的第 $i$ 个通道。$C$ 表示 ${\mathbf{x}}_l$ 中通道的总数。如图 8 所示，平均特征图 ${\overline{\mathbf{x}}}_l$ 内在地包含了有价值的结构信息。因此，骨干因子图 ${\mathbf{\alpha }}_l$ 以与其结构特性一致的方式放大骨干特征图 ${\mathbf{x}}_l$。随后，骨干因子图的确定如下：
$${\mathbf{\alpha }}_l=\left(b_l-1\right)\cdot \frac{{\overline{\mathbf{x}}}_l-\mathrm{Min}\left({\overline{\mathbf{x}}}_l\right)}{\mathrm{Max}\left({\overline{\mathbf{x}}}_l\right)-\mathrm{Min}\left({\overline{\mathbf{x}}}_l\right)}+1\text{, }$$
其中 ${\mathbf{\alpha }}_l$ 表示骨干因子图。$b_l$ 是一个标量常数，并且 $b_l>1$。通过实验调查，我们发现通过与 ${\mathbf{\alpha }}_l$ 乘积不加区分地放大 ${\mathbf{x}}_l$ 的所有通道会在合成图像中产生过度平滑的纹理，如图 9 (b) 所示。原因是 U-Net 强大的去噪能力会在去噪过程中损害图像的高频细节。因此，我们将缩放操作限制在 ${\mathbf{x}}_l$ 的一半通道上，如下所示：
$${\mathbf{x}}_{l,i}^{\prime }=\{\begin{array}{ll}{\mathbf{x}}_{l,i}\odot {\mathbf{\alpha }}_l& \text{ if }i<C/2\\ {\mathbf{x}}_{l,i}& \text{ otherwise }\end{array}$$

因此，骨干因子可以有效地增强 U-Net 的去噪能力并生成更好的图像质量，如图 9 © 所示。

跳跃因子。为了进一步缓解由于增强去噪带来的过度平滑纹理问题，我们进一步在傅里叶域中使用频谱调制，以选择性地减弱跳跃特征的低频分量。数学上，这个操作如下进行：
$$\begin{array}{rl}\mathcal{F}\left({\mathbf{h}}_{l,i}\right)& =\mathrm{FFT}\left({\mathbf{h}}_{l,i}\right)\\ {\mathcal{F}}^{\prime }\left({\mathbf{h}}_{l,i}\right)& =\mathcal{F}\left({\mathbf{h}}_{l,i}\right)\odot {\mathbf{\beta }}_{l,i}\\ {\mathbf{h}}_{l,i}^{\prime }& =\mathrm{IFFT}\left({\mathcal{F}}^{\prime }\left({\mathbf{h}}_{l,i}\right)\right)\end{array}$$
其中 ${\mathbf{h}}_{l,i}$ 表示 U-Net 解码器的第 $l$ 块中跳跃特征图的第 $i$ 个通道。FFT $(\cdot )$ 和 $\mathrm{IFFT}(\cdot )$ 分别是傅里叶变换和逆傅里叶变换。$\odot$ 表示逐元素相乘，而 ${\mathbf{\beta }}_{l,i}$ 是傅里叶掩模，设计为傅里叶系数幅度的函数，用于实现频率依赖的缩放因子 $s_l$：
$${\mathbf{\beta }}_{l,i}(r)=\{\begin{array}{ll}{s}_l& \text{ if }r<r_{\text{thresh }}\\ 1& \text{ otherwise }\end{array}$$
其中 $r$ 是半径。$r_{\text{thresh }}$ 是阈值频率，在我们的实验中设为 1。如图 10 所示，减少跳跃特征的低频分量可以生成更好的细节。

显著的是，所提出的 FreeU 框架不需要任何特定任务的训练或微调。添加骨干和跳跃缩放因子可以通过几行代码轻松完成，提供了更灵活且更强大的去噪操作，而不会增加任何计算负担。这使得 FreeU 成为一种高度实用的解决方案，可以无缝集成到现有的扩散模型中以提高其生成质量。

3. Experiments

3.1. Implementation Details

---

为了评估所提出的 FreeU 的有效性，我们系统地进行了一系列实验，将我们的基准与最先进的方法（如 Stable Diffusion [43, 46]、ModelScope [37]、Dreambooth [47]、ReVersion [23]、Rerender [61]、ScaleCrafter [16]、Animatediff [14] 和 ControlNet [65]）进行了比较。重要的是，我们的方法与这些方法无缝集成，而不会产生与训练或微调相关的任何额外计算开销。我们严格遵循这些方法的规定设置，并在推理过程中专门引入主干特征因子并跳过特征因子。更多消融研究和定量结果可在补充材料中找到。

#scale用于抑制跳跃特征中的低频信息
def Fourier_filter(x, threshold, scale):
    # FFT
    x_freq = fft.fftn(x, dim=(-2, -1))
    x_freq = fft.fftshift(x_freq, dim=(-2, -1))#傅里叶变换
    
    B, C, H, W = x_freq.shape
    mask = torch.ones((B, C, H, W)).cuda() #Beta

    crow, ccol = H // 2, W //2
    mask[..., crow - threshold:crow + threshold, ccol - threshold:ccol + threshold] = scale#阈值内的都用scale放缩
    x_freq = x_freq * mask

    # IFFT
    x_freq = fft.ifftshift(x_freq, dim=(-2, -1))
    x_filtered = fft.ifftn(x_freq, dim=(-2, -1)).real#逆傅里叶变换
    
    return x_filtered

class Free_UNetModel(UNetModel):
    """
    :param b1: backbone factor of the first stage block of decoder.
    :param b2: backbone factor of the second stage block of decoder.
    :param s1: skip factor of the first stage block of decoder.
    :param s2: skip factor of the second stage block of decoder.
    """

    def __init__(
        self,
        b1,
        b2,
        s1,
        s2,
        *args,
        **kwargs
    ):
        super().__init__(*args, **kwargs)
        self.b1 = b1 
        self.b2 = b2
        self.s1 = s1
        self.s2 = s2

    def forward(self, x, timesteps=None, context=None, y=None, **kwargs):
        """
        Apply the model to an input batch.
        :param x: an [N x C x ...] Tensor of inputs.
        :param timesteps: a 1-D batch of timesteps.
        :param context: conditioning plugged in via crossattn
        :param y: an [N] Tensor of labels, if class-conditional.
        :return: an [N x C x ...] Tensor of outputs.
        """
        assert (y is not None) == (
            self.num_classes is not None
        ), "must specify y if and only if the model is class-conditional"
        hs = []
        t_emb = timestep_embedding(timesteps, self.model_channels, repeat_only=False)
        emb = self.time_embed(t_emb)

        if self.num_classes is not None:
            assert y.shape[0] == x.shape[0]
            emb = emb + self.label_emb(y)

        h = x.type(self.dtype)
        for module in self.input_blocks:
            h = module(h, emb, context)
            hs.append(h)
        h = self.middle_block(h, emb, context)
        for module in self.output_blocks:
            hs_ = hs.pop()

            # --------------- FreeU code -----------------------
            # Only operate on the first two stages
            if h.shape[1] == 1280:
                hidden_mean = h.mean(1).unsqueeze(1)
                B = hidden_mean.shape[0]
                hidden_max, _ = torch.max(hidden_mean.view(B, -1), dim=-1, keepdim=True) 
                hidden_min, _ = torch.min(hidden_mean.view(B, -1), dim=-1, keepdim=True)
                hidden_mean = (hidden_mean - hidden_min.unsqueeze(2).unsqueeze(3)) / (hidden_max - hidden_min).unsqueeze(2).unsqueeze(3)

                h[:,:640] = h[:,:640] * ((self.b1 - 1 ) * hidden_mean + 1)#计算backbone特征因子特征图
                hs_ = Fourier_filter(hs_, threshold=1, scale=self.s1)
            if h.shape[1] == 640:
                hidden_mean = h.mean(1).unsqueeze(1)
                B = hidden_mean.shape[0]
                hidden_max, _ = torch.max(hidden_mean.view(B, -1), dim=-1, keepdim=True) 
                hidden_min, _ = torch.min(hidden_mean.view(B, -1), dim=-1, keepdim=True)
                hidden_mean = (hidden_mean - hidden_min.unsqueeze(2).unsqueeze(3)) / (hidden_max - hidden_min).unsqueeze(2).unsqueeze(3)

                h[:,:320] = h[:,:320] * ((self.b2 - 1 ) * hidden_mean + 1)
                hs_ = Fourier_filter(hs_, threshold=1, scale=self.s2)
            # ---------------------------------------------------------

            h = th.cat([h, hs_], dim=1)
            h = module(h, emb, context)
        h = h.type(x.dtype)
        if self.predict_codebook_ids:
            return self.id_predictor(h)
        else:
            return self.out(h)