算法总结

    在2020年的时候，我第一次接触了C++编程，那时的我是一位四年级的小学生，觉得挺好玩的，爸爸就给我推荐了一门课程“程序设计与算法（一）C语言程序设计”，是由北京大学郭炜老师讲解的，他可是北京大学信息学院教师，担任北京大学ACM国际大学生程序设计竞赛队教练多年，北京角斗士软件技术有限公司创始人。

  我从二进制、十进制学起，知道了信息在计算机中的表达方式，学完了入门部分之后，就可以开始做题了，经过郭炜老师的推荐，我找到了一个做题网站OpenJudge，在里面有着郭炜老师创建的小组，里面是每一个单元的例题和习题。

  那天晚上，我记得非常清楚，我和我爸爸第一次找到了OpenJudge网站，已经是夜晚十一点半了，我非常的高兴，告诉他，我今天要把第一题给做出了，他哈哈一笑，对我说：“虽然是第一题，你也不是那么容易做的出来的！”我迅速的浏览起题目“输出第二个整数”，看完之后，我非常的有信心，唰唰几下，双手在键盘上飞速的打着（那时候学术不精，经常会敲错），不过一两分钟的时间（现在看来，太慢了），我点击了提交按钮，刷新了一下“Accepted”，竟然对了！

  这就是我做的第一道编程题：

#include <iostream>
using namespace std;
int main()
{
	int a;
	int b;
	int c;
	cin>>a;
	cin>>b;
	cin>>c;
	cout<<b<<endl;
	return 0;
}

该题文章： http://t.csdn.cn/GzEaJhttp://t.csdn.cn/GzEaJ

  因为我成功做对了一道题，所以我继续朝第二题看去，十分钟过后......我依旧没有做出来，我百思不得其解，这时候，一道声音传来，打断了我的思路：“小荣，已经12点钟了，快点睡觉了，明天继续搞也不迟啊！” 就这样，我带着疑惑沉沉的入睡了。

  就这样，我保持着半混半学的状态学习了一年，在五年级的寒假，我连程序设计与算法（一）都还没有学完，于是开始认真搞，先从“程序设计与算法（一）”中我最薄弱的位运算开始，“>>、<<、&、*……”，然后开始学习最有难度的指针，那时候，我做的很多题都用不到指针，认为指针只是在多此一举罢了，后来我才知道指针就是很多著名算法里最重要的部分“二叉树、链表B+树等等”。

  五年级下册开学之后，我的程序设计与算法（一）还有3个单元没有上完，但是因为时间紧迫，我开始学起了算法，也是郭炜老师的一门课程“程序设计与算法（二）算法基础”，第一单元是枚举算法，我想：枚举，不就是for循环一个一个去算嘛！

  当我遇到了枚举算法的第四个例题“熄灯问题”，啊，这怎么枚举啊，难不成是把所有按钮状态一一枚举，那时间复杂度可就到了恐怖的O(2^30)，所以枚举也有不同的枚举方法，例如我刚刚说的这个，复杂度超大的被称为“超暴力枚举”，在爸爸那里，我了解到，可以进行二进制0,1的枚举，这道题的状态也刚好是0,1，在经过长时间的手算之后，我们终于把发现了规律，只用枚举第一行的，只需要2^6，后面的就可以根据第一行按的推出来。

  于是，我运用了刚学了不久的位运算（专门针对二进制的一种运算），编写了一串超长的代码，时间复杂度勉强过得去，这种叫做“暴力枚举”，至于最快的普通“枚举”，是很难想出来的。

#include <iostream>
using namespace std;
int main()
{
	int a[5][6],b[5][6],c[5][6],d[5][6],m=0;
	for(int i=0;i<5;i++)
	{
		for(int j=0;j<6;j++)
		{
			cin>>a[i][j];
			c[i][j]=a[i][j];
		}
	}
	int l=1,k,sum[100],x,y,o=0,e=0;
	while(l!=0)
	{
		m=0;
		while(l!=0&&e!=64)
		{
        	for(int i=0;i<5;i++)
	        {
		        for(int j=0;j<6;j++)
		        {
			        a[i][j]=c[i][j];
		        }
	        }
            int p;
            p=e;
            k=0;
	        while(p!=0)
	        {
		        sum[k]=p%2;
		        p=p/2;
		        k++;
	        }
	        for(int i=0;i<=0;i++)
	        {
	        for(int j=0;j<6;j++)
	        {
                b[i][j]=sum[5-j];
                d[i+4][j]=b[i][j];
            }
            for(int j=5;j>=0;j--)
            {
			    if(b[i][j]==1)
			    {
				    if(a[i][j]==0)
				    { 
					    a[i][j]=1;
				    }
				    else if(a[i][j]==1)
				    {
					    a[i][j]=0;
				    }
				    if(a[i+1][j]==0&&(i+1)<=4)
		    	    {
			    	    a[i+1][j]=1;
			        }
			        else if(a[i+1][j]==1&&(i+1)<=4)
			        {
				        a[i+1][j]=0;
			        } 
			        if(a[i][j+1]==0&&(j+1)<=5)
			        {
				        a[i][j+1]=1;
			        }
			        else if(a[i][j+1]==1&&(j+1)<=5)
			        {
				        a[i][j+1]=0;
			        } 
			        if(a[i-1][j]==0&&(i-1)>=0)
		    	    {
			    	    a[i-1][j]=1;
			        }
			        else if(a[i-1][j]==1&&(i-1)>=0)
			        {
				        a[i-1][j]=0;
			        }    
			        if(a[i][j-1]==0&&(j-1)>=0)
			        {
				        a[i][j-1]=1;
			        }
			        else if(a[i][j-1]==1&&(j-1)>=0)
			        {
				        a[i][j-1]=0;
			        }   		
			    }
			}
		    }			
	        for(int i=0;i<4;i++)
	        {
	        for(int j=0;j<6;j++)
	        {
                b[i][j]=a[i][j];
            } 
            for(int j=5;j>=0;j--)
            {
			    if(b[i][j]==1)
			    {
			        if(a[i+1][j]==0)
			        {
				        a[i+1][j]=1;
			        }
			        else if(a[i+1][j]==1)
			        {
				        a[i+1][j]=0;
			        }
			        if(a[i+2][j]==0&&(i+2)<=4)
		            {
			   	        a[i+2][j]=1;
			        }
			        else if(a[i+2][j]==1&&(i+2)<=4)
			        {
			            a[i+2][j]=0;
			        } 
			        if(a[i+1][j+1]==0&&(j+1)<=5&&(i+1)<=4)
			        {
			            a[i+1][j+1]=1;
			        }
			        else if(a[i+1][j+1]==1&&(j+1)<=5&&(i+1)<=4)
			        {
			            a[i+1][j+1]=0;
			        } 
			        if(a[i][j]==0&&i>=0)
		            {
			   	        a[i][j]=1;
			        }
			        else if(a[i][j]==1&&i>=0)
			        {
			            a[i][j]=0;
			        }    
			        if(a[i+1][j-1]==0&&(j-1)>=0&&(i+1)<=4)
			        {
			            a[i+1][j-1]=1;
			        }
			        else if(a[i+1][j-1]==1&&(j-1)>=0&&(i+1)<=4)
			        {
			            a[i+1][j-1]=0;
			        }     		
			    }
			}
		}
            if(a[4][0]==0&&a[4][1]==0&&a[4][2]==0&&a[4][3]==0&&a[4][4]==0&&a[4][5]==0)
            {
            	l=0;
			}	
			e++;			    
		}
	} 
	
	for(int i=4;i<=4;i++)
	{
		for(int j=0;j<6;j++)
		{
			if(d[i][j]>1)
			{
				d[i][j]=0;
			}
			cout<<d[i][j]<<" ";
		}
	}
	cout<<endl;	
	for(int i=0;i<4;i++)
	{
		for(int j=0;j<6;j++)
		{
			cout<<b[i][j]<<" ";
		}
		cout<<endl;
	}
    return 0;
} 

  在学习完枚举算法（2个星期）之后，我开始学习递归算法，递归，就是在一个函数里调用表自己，可能有人会疑问：“这样下去不没完没了吗？”确实，所以我们需要在函数里面加一个递归终止条件。

  看了关于递归的题目之后，我发现，递归的题目看起来简单，但是编起来难（虽说递归题的代码都很短），于是，我花了很多的时间学递归，每一道题都用了几天的时间，爸爸说：“递归就是最重要的算法之一！”后来，我了解到，递归确实很重要，在动态规划中，递推中，深度、广度搜索中，都需要递归来做基础。

  几天后，我遇到了有史以来最难的一道递归算法题“表达式求值”，输入一个字符串，里面是一个表达式，包含+、-、*、/、（），输出表达式的值，首先，我们知道同级运算，从左到右依次计算，有括号，先算括号里的，在算括号外的，所以，我们一个需要3个递归函数，3个函数互相调用。

  第一个函数是用来读取里面的数字和判断是否有括号的，然后返回给另外两个函数来计算，第二个函数是来进行乘除法运算的，第三个函数是来进行加减运算的。

  这道题，我苦思冥想、绞尽脑汁都没有想出来，所以只好看了答案：

#include <iostream>
#include <cstring>
#include <cstdlib>
using namespace std;
int factor_value();
int term_value();
int expression_value();
int factor_value()
{
    int result1=0;
    char c=cin.peek();
    if(c=='(') 
    {
        cin.get();
        result1=expression_value();
        cin.get();
    }
    else 
	{
        while(isdigit(c)) 
		{
            result1=10*result1+c-'0';
            cin.get();
            c=cin.peek();
        } 
    }
    return result1;
}
int term_value() 
{
    int result2=factor_value();
    while(true) 
	{
        char op = cin.peek();
        if(op=='*'||op=='/')
		{
            cin.get();
            int value1=factor_value();
            if(op=='*') 
              result2*=value1;
            else result2/=value1;
        }
        else 
          break;
    }
    return result2;
}
int expression_value()
{
	int result=term_value();
    bool more=true;
    while(more) 
	{
        char op=cin.peek();
        if(op=='+'||op=='-') 
		{
            cin.get();
            int value=term_value();
            if(op=='+') result+=value;
            else result-=value;
        }
        else more=false;
    }
    return result;
}
int main()
{
    cout << expression_value() << endl;
    return 0;
}

  之后， 还有一道递归题“算24”，和这道题的类型差不多，就只是复杂一点，需要用到枚举算法，在这里就不多说了。

  学完了递归，我的速度就提上来了，开始学习二分算法，也是真正了解了所谓的时间复杂度和空间复杂度。二分算法，顾名思义，就是不断的分成两段，那分成两半来干嘛呢？第一，二分算法也可以成为二分搜索算法，注意‘搜索’，可以是在一串数中找一个数，也可能是你在1000以内找到一个数（这个数随机数）第二，二分算法就是来优化时间复杂度的。

  我们来举一个例，在1000以内找到一个数（这个数随机数），如果按照普通的程序，需要for(int i=1;i<=1000;i++）这样来寻找，时间复杂度为O（log n），所以我们可以将1000分为两半，就是500，判断一下这个数大于500还是小于500，然后继续二分，最多就搜寻10次，也就是O（log 10）(2^10=1024)，你看，这个二分法优化了许多吧。

  其中有一道例题是这样的，输入n（n<=10000）个数，在里面找出两个数，这两个数的和等于m，如果按照正常思维的话，时间复杂度是O（log n^2），如果用二分的话，可以先将将数组排序，复杂度是O(nlog(n))，然后对数组的每个元素a[i],在数组中二分查找m-a[i],看能否找到。复杂度log(n),最坏要查找n-2次，所以查找这部分复杂度也是O(nlog(n))。

  这道题可不仅仅只能用二分法解决，还可以运用双指针：

#include<bits/stdc++.h>
using namespace std;
int arr[10005];
int main()
{
	int n,m;
	cin>>n>>m;
	for(int i=0;i<n;i++)
	  cin>>arr[i];
	sort(arr,arr+n);
	int i,j=n-1;
	while(arr[i]+arr[j]!=m)
	{
		if(arr[i]+arr[j]>m) 
		  j--; 
		else if(arr[i]+arr[j]<m) 
		  i++;
	} 
	cout<<arr[i]<<" "<<arr[j]<<endl;
	return 0;
}

别看这段代码中根本没有显示指针的影子，其实其中的i,j都是指针，分别代表着两个数的下标。 

  在学完二分算法以后，接下来学的就是分治算法了，分治，顾名思义，也是要分的，一些著名的排序算法就运用了分治算法，如快速排序、归并排序，其中归并排序在很大程度上都是分治，快速排序就不同了，只有小部分运用有分治，其它大部分都是之前我说过的“双指针算法”。

以下两个链接是关于快速排序和归并排序的：

http://t.csdn.cn/YiBOkhttp://t.csdn.cn/YiBOkhttp://t.csdn.cn/78IG0http://t.csdn.cn/78IG0  我们来看一道分治算法典型的一道例题“输出前m大的数”，首先，它没有说输入的数必须是升序排列，所以我们要自己排序，需要自己编一个函数，实现快速排序或者归并排序（个人建议用归并排序，因为快速排序最差的情况是O（n^2）），因为是输出前m大的数，所以要进行从大到小排列后（只需要改快速排序的判断条件就可以了），依次输出a[0)——a[m-1]就可以了。

  其实还有一种更简单的方法，不过复杂度很高，就是在STL库里面运用函数sort（冒泡排序，复杂度为O(n^2)），如果要从大到小排序的话，需要定义一个函数。

#include <iostream>
#include<bits/stdc++.h>
using namespace std;
bool cmp(int a, int b)
{
	return a>b; 
}
int main()
{
	int n,k;
	cin>>n;
	int a[n];
	for(int i=0;i<n;i++)
	  cin>>a[i];
	cin>>k;
	sort(a,a+n,cmp);
	for(int i=0;i<k;i++)
	  cout<<a[i]<<endl;
	return 0;
}

    在学习完了分治算法之后，就到了一个非常难的部分了，那就是“动态规划（俗称dp）”，动态规划也是，顾名思义，是在递归里面设置一个动态的变量，因为递归中难免会递归重复的地方，所以做一个标记的话，遇到重复的地方，直接下一步。

  动态规划的基本思想是将待求解的问题分解成若干个相互联系的子问题，先求解子问题，然后从这些子问题的解得到原问题的解。对于重复出现的子问题，只在第一次遇到的时候对它进行求解，并把答案保存起来，让以后再次遇到时直接引用答案，不必重新求解。

    动态规划呢，它是求最优性问题的一种常用方法，难度比较大，技巧性也很强，动态规划可以比贪心算法、分治算法优雅而高效的解决很多问题。

  我们来看一道最典型的例题吧“最大子段和” ，令b[j]表示以位置 j 为终点的所有子区间中和最大的一个子问题:如j为终点的最大子区间包含了位置j-1,则以j-1为终点的最大子区间必然包括在其中，如果dp[j-1] >0, 那么显然dp[j] = dp[j-1] + ty[j]，用之前最大的一个加上a[j]即可，因为seq[j]必须包含如果dp[j-1]<=0,那么dp[j] = ty[j] ,因为既然最大，前面的负数必然不能使你更大。

  一个简易的代码：

#include<iostream>
#include<algorithm>
using namespace std;
int n;
int m;
int main()
{
	while(cin>>n)
	{
		m=-1000000;
		int ty;
		int tm=0;
		for(int i=1;i<=n;i++)
		{
			cin>>ty;
			if(tm>=0)
			  tm+=ty;
			if(tm<0)
			  tm=ty;
			m=max(m,tm);
		}
		cout<<m<<endl;
	}
	return 0;
}

运用动态规划后，该代码复杂度为O(n)。 

  之后，就开始了基础图论的学习，首先学习的就是深度优先搜索，跟名字一样，要深度，就是要走的远一点，把所有的路全部走一遍，然后找出最优路径，由于要把所有路都走一遍，循环肯定是行不通了，那就要用递归了（也可以用更高级的递推），在函数之中，就可以互相比较了，找出其中最优的一个，然后继续跟下一组数据比较，以此循环，直到走到了路的尽头（没有没有走过的路了），就停止，然后往回走，走到发现一条没有走过的路为止。

  深度优先搜索这个算法，好是好，不过有一些费时，所以需要用什么方法来优化一下，用什么方法呢？那当然是“剪枝”了！

  剪枝分为两种，一种是可行性剪枝，另外一种是最优性剪枝，最优性剪枝是：还没有走到终点，用的时间就已经超过了之前成功走到的终点的时间，自然是没有走下去的必要了。可行性剪枝是：在走的过程中，发现无论怎么走都走不到终点，就停止行走。

  来看深度优先搜索经典题型“城堡问题”，首先要判断是否已经访问过，若是，直接返回(return )然后要进行访问操作，最后运行递归。

其实就是找最大的连通图的大小。可以向四个方向走：

#include<iostream>
#include<stdio.h>
#include<cstring>
using namespace std;
int map[55][55],v[55][55]; 
int n,m,sum,a,mx=0;
void dfs(int i,int j)
{
	if(v[i][j])
	  return ;
	v[i][j]=sum;
	a++;
	if((map[i][j]&1)==0) 
	  dfs(i,j-1);
	if((map[i][j]&2)==0) 
	  dfs(i-1,j);
	if((map[i][j]&4)==0) 
	  dfs(i,j+1);
	if((map[i][j]&8)==0) 
	  dfs(i+1,j);
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	  for(int j=1;j<=m;j++)
	    cin>>map[i][j]; 
	memset(v,0,sizeof(v));
	for(int i=1;i<=n;i++)
	{
	    for(int j=1;j<=m;j++)
		{
		    if(!v[i][j])
			{
			    sum++;
			    a=0;
			    dfs(i,j);
	    	    mx=max(a,mx);
		    }
	    }
    }
    cout<<sum<<endl;
	cout<<mx<<endl;
	return 0;
} 

记住，做这种题的时候，最开始一定要数组初始化！（memset） 

  深度优先搜索学完了，就可以学广度优先搜索了，广度，就是给节点分层，起点是第0层，从起点最少用n步到达的点属于第n层，然后依层次顺序，从小到大扩展节点，把层次低的点全部扩展出来后，再扩展层次高的点，这也是用递归来实现（注意，扩展时，不能扩展出已经走过的点）

  宽度优先搜索与深度优先搜索一样，都会生成所有能遍历到的状态，因此需要对所有状态进行处理时使用宽度优先搜索也是可以的。但是递归函数可以很简短地编写，而且状态的管理也更简单，所以大多数情况下还是使用深度优先搜索实现。反之，在求最短路时，深度优先搜索需要反复讲过相同的状态，所以此时还是使用宽度优先搜索比较好。
  宽度优先搜索会把状态逐个加入队列，因此通常需要与状态数成正比的内存空间。深度优先搜索是与最大的递归深度成正比的，一般与状态数相比，递归的深度不会太大，所以可以认为深度优先搜索更加节省空间。

以下是广度优先搜索结构图:

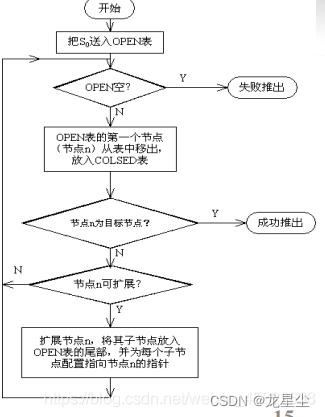
   然后，我们看一下广度优先搜索的经典题目“抓住那头牛”，按照距开始状态由远及近的顺序进行搜索，因此可以很容易用来求最短路径，在这里，我们可以枚举一下这三种走路方法，直到走到终点为止，注意，在广度优先搜索中，最先到终点的一定是最优的。

一般来说，这种图论题都是BFS：

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
struct no
{
    int x;
    int s;
};
int d[3]={-1,1,2};
int n,k;
int v[100010];
void BFS()
{
    memset(v,0,sizeof(v));     
    no st,e;
    queue<no> s;
    st.x=n;
    st.s=0;
    v[st.x]=1;
    s.push(st);
    while(!s.empty())
    {
        st=s.front();
        s.pop();
        if(st.x==k)
        {
            cout<<st.s<<endl;
            return;
        }
        for(int i=0;i<3;i++)
        {
            if(i==2)
            {
                e.x=st.x*2;
                e.s=st.s+1;  
            }
            else
            {
                e.x=st.x+d[i];
                e.s=st.s+1;
            }
            if(e.x<=100000&&e.x>=0&&v[e.x]==0)
            {   
                v[e.x]=1;
                s.push(e);
            }
        }
    }
}
int main()
{

    cin>>n>>k;
    if(n<=k)
      BFS();
    else
      cout<<n-k<<endl;
    return 0;
}

  当我学完了最基础的图论之后，就开始学贪心算法了。贪心算法，跟名字一样，很贪心，一般类型题都是把自己的钱花光，买更多的东西，如果是贪心一类的题目，一般都需要排序，那我们怎么将多组对应的数据排序呢（一个一个排序要打乱顺序），当然是程序设计与算法（一）中学习吧过的结构体了，将结构体排序，自然是对应的。

  贪心算法常以当前情况为基础根据某个优化测度作最优选择，而不考虑各种可能的整体情况，它省去了为找最优解要穷尽所有可能而必须耗费的大量时间，它采用自顶向下，以迭代的方法做出相继的贪心选择，每做一次贪心选择就将所求问题简化为一个规模更小的子问题，通过每一步贪心选择，可得到问题的一个最优解，虽然每一步上都要保证能获得局部最优解，但由此产生的全局解有时不一定是最优的。

   接下来，我们来看一道贪心题目“圣诞老人的礼物”，看题目就知道，果然很贪心，能拿多少就拿那多少。对于这个问题，我们可以采取贪心算法，因为他考虑的是眼前的利益，可以用替换法来证明。为此我们要利益最大化，便必须把糖果的价值与重量的比值来判别，比值越大，便能取得最大的利益。我们可以采取结构体来存储，通过algorithm(C++的一个头文件)中的sort函数来进行排序。

#include<bits/stdc++.h>
using namespace std;
const double eps = 1e-6;
struct Candy 
{
    int v; 
	int w;
	bool operator<(const Candy&c) const
	{
	    return double(v)/w-double(c.v)/c.w>eps; 
	}
}cand[110]; 
int main() 
{
    int n,w;
    cin>>n>>w;
	for(int i = 0;i < n; ++i) 
	  cin>>cand[i].v>>cand[i].w;
	sort(cand,cand+n);
	int tw=0;
	double tv=0;
	for(int i=0;i<n;i++) 
	{
	    if(tw+cand[i].w<=w) 
		{
            tw+=cand[i].w;
            tv+=cand[i].v; 
        }
        else 
		{
		    tv+=cand[i].v*double(w-tw)/cand[i].w;
			break;
        }
    }
    printf("%.1f",tv);
    return 0;
}

贪心它用的就是替换法 

  终于，我把郭炜的程序设计与算法（二）学完了，凭借我个人的感受，以及一些算法的难度，我得知：在这些基础算法中，动态规划(dp)是我认为最难的算法，首先，它需要递归来作为它的基础，然后升级为递推，并且还要排除重复的，其次，在函数中需要定义一个会“动”的变量，以此来作为一个标记。

  然后，我认为最简单（也不能说是简单吧，总而言之就是基础中的基础）的就是分治算法，感觉就是在铺地砖，为一些排序算法(快排、归并)铺地砖，也帮助我们更好的理解二分算法，因为两个算法有些地方我感觉一样，然后分治算法一般的代码是要短一些，而二分算法代码比较长一些，那两者的区别吧是什么呢？那就是时间复杂度了，一般的题目来说，二分算法的速度要快一些，那分治算法的优点是什么呢？当然是可以解决一些二分算法解决不了的问题。

  本门课程要求学习者已经掌握C语言，以及基本的程序设计思想。本课程将讲述枚举、递归、分治、动态规划、搜索这几种算法。一部分内容，难度与中学信息学奥赛NOIP提高组的较难题，ACM国际大学生程序设计竞赛中的中等题相当。学好本课程，算法及实现能力将超过国内大部分高校计算机专业本科毕业生。

                                                                                                                      —— 课程团队

  以上是郭炜老师的团队说的话，我将在今年9月份参加普及组竞赛，而这门课程中的题竟然已经相当于提高组难度了，这些题我肯定不会的，所以说我的算法实现能力比高校计算机专业本科毕业生差上很多，这就是我这2年来的学习总结，谢谢大家。

  以下是我这1年内编程的提交图片:

  

 

 

 

这个XJOI是我最近几天才开始的，所以等级不高，嘿嘿嘿!