JCR1区电鳗觅食优化算法(EEFO)，原理详解，MATLAB代码免费获取

电鳗觅食优化算法（Electric eel foraging optimization:，EEFO）是一种受自然启发的群智能优化算法。该算法电鳗是动物界非凡的掠食者。电鳗来自南美洲的裸鱼科，以其在淡水鱼中惊人的放电能力而闻名。电鳗的物理结构和产电器官如下图所示。鳗鱼由于视力不佳，通常产生大约10伏的电压来导航和定位猎物。鳗鱼利用这些电信号的反馈来有效地跟踪和精确地定位快速移动的猎物。在进行群体狩猎时，鳗鱼倾向于聚集在一起，绕圈游动，将鱼群驱赶成一个“猎物球”，然后共同对猎物球发动掠夺性高压攻击。这种群体狩猎行为增加了获得更多猎物的机会，尤其是在鱼类丰富的情况下。受这些优化行为的启发，EEFO被设计出来。

该成果于2024年发表在计算机领域一区期刊Expert Systems with Applications上，目前在谷歌学术上查询被引率12次。

EEFO有四种觅食行为，包括互动、休息、狩猎和迁徙。模仿互动行为是为了更好地探索，模仿休息、狩猎和迁徙行为是为了更好地开发。EEFO中使用的能量因子改善了勘探与开发之间的平衡。

1、算法原理

（1）相互作用

当鳗鱼遇到一群鱼时，它们通过游泳和相互搅动来相互作用。然后，鳗鱼开始在一个巨大的通电圆圈中游泳，在圆圈中心捕获许多小鱼。在EEFO中，每条电鳗都是一个候选解，每一步得到的最佳候选解被认为是目标猎物。这种相互作用表明，每条鳗鱼都利用鳗鱼的位置信息与其他个体进行合作互动。这种行为可以看作是全局勘探阶段。具体来说，电鳗可以通过使用种群中所有个体的位置信息，与从种群中随机选择的任何鳗鱼进行互动。更新鳗鱼的位置包括比较随机选择的鳗鱼和流行中心之间的差距。

此外，电鳗可以利用搜索空间中的区域信息与种群中随机选择的其他鳗鱼进行交互。通过确定从种群中随机选择的鳗鱼和在搜索空间中随机生成的鳗鱼之间的差异来更新鳗鱼的位置。鳗鱼之间的相互作用以搅动为标志，它表示在不同方向上的随机运动。下面的模型表示这种变动。

其中T是最大迭代次数。交互行为可以定义为:

其中T是最大迭代次数。交互行为可以定义为:式中，p1和p2为(0,1)内的随机数，fit(x(i))为第i条电鳗候选位置的适应度，xj为从当前种群中随机选择的电鳗位置，j≠ i, n为种群大小，r1为(0,1)内的随机数，r为(0,1)内的随机向量，Low和Up分别为下限和上限。由公式可知，这种相互作用行为使得电鳗在搜索空间中向不同位置移动，对整个搜索空间中EEFO的探索有很大的帮助。

（2）休息

在EEFO中，应在电鳗进行休息行为之前建立休息区。为了提高搜索效率，将鳗鱼位置向量的任意一维投影到搜索空间的主对角线上，在该区域建立一个休息区域。为了确定鳗鱼的休息区域，搜索空间和鳗鱼的位置都归一化为0-1的范围。鳗鱼位置的一个随机选择的维度被投射到归一化搜索空间的主对角线上。投影位置被认为是鳗鱼休息区域的中心。下图显示了分别在二维和三维空间中确定鳗鱼休息区域的程序。休息区域可以描述为:

其中xprey是迄今为止得到的最优解的位置向量，α0是休息区的初始尺度， 表示休息区的范围， 是从当前种群中随机选择的个体的随机位置维数，Z是归一化数。因此，在进行休息行为之前，在其休息区域内获得鳗鱼的休息位置:

其中α为静息区的尺度，r2为(0,1)内的随机数。尺度α使静息区的范围随着迭代的进行而减小。这将加强剥削。

当休息区域确定后，鳗鱼会移到休息区域。也就是说，鳗鱼用它在休息区内的休息位置来更新它朝向休息区域的位置。静息行为可以表示为:

（3）狩猎

当鳗鱼发现猎物时，它们不只是成群结队地去捕猎。相反，它们倾向于合作游成一个大圈，包围猎物。同时，它们通过低电器官放电不断地与同伴交流和合作。随着电鳗相互作用的增强，电气化圈减小。最后，鳗鱼把鱼群从较深的一端驱赶到较浅的一端，在那里它们很容易成为猎物。基于这种行为，通电的圆圈成为狩猎区域，此时，猎物开始在狩猎区域内四处奔跑，因此猎物会因为受到惊吓而突然连续地从当前位置移动到狩猎空间内的其他位置。狩猎区域可以定义为:

式中，β0为狩猎区域的初始尺度。由公式可知，鳗鱼以猎物xprey为中心，其捕猎范围由 决定

因此，可以生成一个新的灰色位置，即它在狩猎区域内的预先位置：

其中β为狩猎区域的尺度，r3为(0,1)范围内的随机数。尺度β使狩猎区域的范围随着时间的推移而变小。这有利于开发。

在确定狩猎区域后，鳗鱼开始在狩猎区域执行猎物。在捕猎时，鳗鱼会迅速定位猎物的新位置，并卷曲头部和尾部，将猎物夹在中间，并在灰色周围发出高压电流。在EEFO中观察到的狩猎行为包括一个卷曲的运动，在这个运动中，鳗鱼的位置被更新到猎物的新位置。鳗鱼在狩猎过程中所表现出的卷曲行为可以描述如下:

式中η表示卷曲因子，定义为:

其中r4是(0,1)范围内的随机数。

鳗鱼的捕猎行为如图所示。当猎物被鳗鱼包围时，一些灰色的位置足迹被红点所标记，因为猎物进行了天鹅跳水。在这一点上，鳗鱼通过卷曲的行为来冲击猎物，并且位置足迹用于在下一次迭代中更新鳗鱼的新位置。

（4）迁移

当鳗鱼发现猎物时，它们往往会从休息区迁移到捕猎区。为了对鳗鱼的迁徙行为进行数学建模，我们使用了以下公式:

其中Hr可以认为是狩猎区域内的任意位置，r5和r6是(0,1)内的随机数。(Hr(t + 1)-xi(t))表示鳗鱼向捕猎区移动。L为Levy飞行函数，为了避免陷入局部最优，在EEFO的开发阶段引入了Levy飞行函数。

其中Γ为标准伽马函数，b = 1.5。下图描述了鳗鱼迁徙行为的模式图。

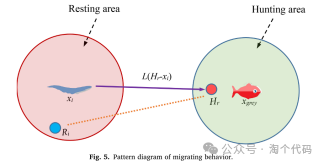
鳗鱼可以通过低放电感知猎物的位置，因此它可以随时调整自己的位置。如果鳗鱼在觅食过程中感觉到猎物的靠近，它们就会移动到候选位置;否则，鳗鱼将停留在当前位置。鳗鱼的位置由更新:

（5）从勘探到开发的过渡

在EEFO中，搜索行为由能量因子决定，可以有效地管理探索与开发之间的过渡，从而提高算法的优化性能。鳗鱼的能量因子值用于选择勘探还是开采。能量因子定义为:

其中r7是(0,1)范围内的随机数。由下式可知，E(t)随迭代次数的增加而减小，能量因子E(t)在迭代过程中随振荡呈减小趋势。当能量因子E(t)大于1时，鳗鱼通过交互行为在整个变量空间内进行全局搜索，从而进行探索。当能量因子E(t)小于或等于1时，鳗鱼倾向于通过迁徙、休息或狩猎等行为在有希望的子区域进行局部搜索，从而导致开发。在迭代的前半部分，探索以较高的概率发生，而在迭代的后半部分，开发以较高的概率发生。图6描述了E在500次迭代中的行为。

为了研究EEFO的搜索行为，在整个优化过程中对eb> 1的概率进行了评估。

让 

然后 

E > 0的概率由下式获得：

根据公式，在优化过程中，在勘探或开采之间执行的概率大约为50%。它有助于平衡勘探和开发。

2、伪代码流程

3、结果展示

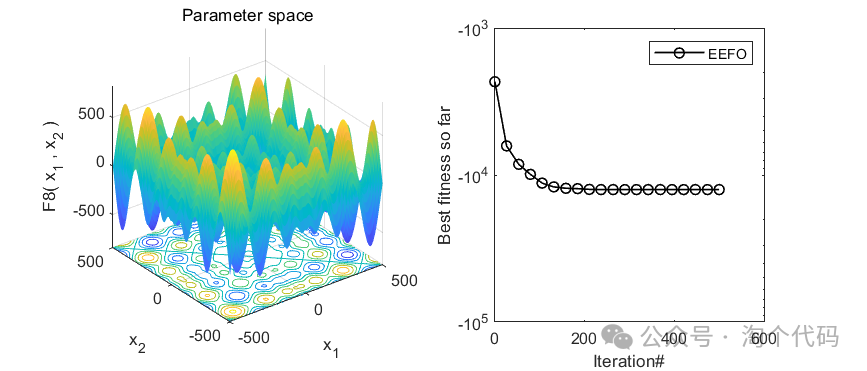
4、MATLAB核心代码

% Electric Eel Foraging Ooptimization (EEFO) for 23 functions             %
% EEFO code v1.0.                                                         %
% Developed in MATLAB R2018b                                              %
% --------------------------------------------------------------------------
    function [Xprey,BestF,HisBestF]=EEFO(FunIndex,MaxIt,PopSize)
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    % FunIndex: Index of function.                       %
    % MaxIt: Maximum number of iterations.               %
    % PopSize: Size of population.                       %
    % PopPos: Position of rabbit population.             %
    % PopFit: Fitness of population.                     %
    % Dim: Dimensionality of prloblem.                   %
    % Xprey: Best solution found so far.                 %
    % BestF: Best fitness corresponding to Xprey.        %
    % HisBestF: History best fitness over iterations.    %
    % Low: Low bound of search space.                    %
    % Up: Up bound of search space.                      %
    % E:Energy factor.                                   %
    % Alpha:scale of resting area.                       %
    % Beta: scale of hunting area.                       %
    % Eta: Curling factor.                               %
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    [Low,Up,Dim]=FunRange(FunIndex);
    if length(Low)==1
        lb=Low*ones(1,Dim);
        ub=Up*ones(1,Dim);
    else
        lb=Low;
        ub=Up;
    end
    PopPos=zeros(PopSize,Dim);
    PopFit=zeros(1,PopSize);
    for i=1:PopSize
        PopPos(i,:)=rand(1,Dim).*(ub-lb)+lb;
        PopFit(i)=PopFit(1);
    end
    BestF=BenFunctions(PopPos(1,:),FunIndex);
    Xprey=PopPos(1,:);
    for i=2:PopSize
        if PopFit(i)<=BestF
            BestF=PopFit(i);
            Xprey=PopPos(i,:);
        end
    end
    HisBestF=zeros(MaxIt,1);

    for It=1:MaxIt
        DirectVector=zeros(PopSize,Dim);
        E0=4*sin(1-It/MaxIt);
        for i=1:PopSize
            E=E0*log(1/rand);% Eq.(30)

            if Dim==1
                DirectVector(i,:)=1;
            else
                RandNum=ceil((MaxIt-It)/MaxIt*rand*(Dim-2)+2);%Eq.(6)
                RandDim=randperm(Dim);
                DirectVector(i,RandDim(1:RandNum))=1;
            end
            if E>1
                K=[1:i-1 i+1:PopSize];
                j=K(randi(PopSize-1));
                %Eq.(7),interacting
                if PopFit(j)<PopFit(i)
                    if rand>0.5
                        newPopPos=PopPos(j,:)+randn*DirectVector(i,:).*( mean(PopPos)-PopPos(i,:));
                    else
                        xr=rand(1,Dim).*(ub-lb)+lb;
                        newPopPos=PopPos(j,:)+1*randn*DirectVector(i,:).*( xr-PopPos(i,:));
                    end
                else
                    if rand>0.5
                        newPopPos=PopPos(i,:)+randn*DirectVector(i,:).*(mean(PopPos)-PopPos(j,:));
                    else
                        xr=rand(1,Dim).*(ub-lb)+lb;
                        newPopPos=PopPos(i,:)+randn*DirectVector(i,:).*( xr-PopPos(j,:));
                    end
                end
            else
                if rand<1/3
                    % resting
                    Alpha=2*(exp(1)-exp(It/MaxIt))*sin(2*pi*rand); % Eq.(15)
                    rn=randi(PopSize);
                    rd=randi(Dim);
                    if length(Low)~=1
                        z=(PopPos(rn,rd)-lb(rd))/(ub(rd)-lb(rd));% Eq.(13)
                        Z=lb+z*(ub-lb);% Eq.(12)
                    else
                        Z=PopPos(rn,rd)*ones(1,Dim);
                    end
                    Ri=Z+Alpha.*abs(Z-Xprey);% Eq.(14)
                    newPopPos=Ri+randn*(Ri-round(rand)*PopPos(i,:));% Eq.(16)
                elseif rand>2/3
                    % migrating
                    rn=randi(PopSize);
                    rd=randi(Dim);
                    if length(Low)~=1
                        z=(PopPos(rn,rd)-lb(rd))/(ub(rd)-lb(rd));
                        Z=lb+z*(ub-lb);
                    else
                        Z=PopPos(rn,rd)*ones(1,Dim);
                    end
                    Alpha=2*(exp(1)-exp(It/MaxIt))*sin(2*pi*rand);
                    Ri=Z+Alpha.*abs(Z-Xprey); % resting area
                    Beta=2*(exp(1)-exp(It/MaxIt))*sin(2*pi*rand);%Eq.(21)
                    Hr=Xprey+Beta*abs(mean(PopPos)-Xprey);%Eq.(25) hunting area
                    L=0.01*abs(levy(Dim)); %Eq.(26)
                    newPopPos=-rand*Ri+rand*Hr-L.*(Hr-PopPos(i,:));%Eq.(24)
                else
                    %Hunting
                    Beta=2*(exp(1)-exp(It/MaxIt))*sin(2*pi*rand);%Eq.(21)
                    Hprey=Xprey+Beta*abs(mean(PopPos)-Xprey);% Eq.(20) hunting area
                    r4=rand;
                    Eta=exp(r4*(1-It)/MaxIt)*(cos(2*pi*r4)); %Eq.(23)
                    newPopPos=Hprey+Eta*(Hprey-round(rand)*PopPos(i,:));%Eq.(22) hunting
                end
            end
            newPopPos=SpaceBound(newPopPos,ub,lb);
            newPopFit =BenFunctions(newPopPos,FunIndex);
            if newPopFit<PopFit(i)
                PopFit(i)=newPopFit;
                PopPos(i,:)=newPopPos;
                if PopFit(i)<=BestF
                    BestF=PopFit(i);
                    Xprey=PopPos(i,:);
                end
            end
        end
        HisBestF(It)=BestF;
    end

参考文献

[1]Zhao W, Wang L, Zhang Z, et al. Electric eel foraging optimization: A new bio-inspired optimizer for engineering applications[J]. Expert Systems with Applications, 2024, 238: 122200.

完整代码获取

后台回复关键词：

TGDM899