2024年JCR一区新算法：鹭鹰优化算法，原理详解，MATLAB代码免费获取

鹭鹰优化算法（Secretary bird optimization algorithm，SBOA）是一种受自然启发的群智能优化算法，灵感来自于鹭鹰在自然环境中的生存行为。鹭鹰的生存需要不断地捕猎猎物和逃避捕食者的追捕。SBOA在解决方案质量、收敛速度和稳定性方面的出色性能。该成果于2024年发表在知名一区SCI期刊Artificial Intelligence Review上。

SBOA利用鹭鹰的生存能力，以解决现实世界的优化问题。该算法的探索阶段模拟鹭鹰狩猎蛇，而开发阶段模拟它们逃离捕食者。在这个阶段，鹭鹰观察环境，并选择最合适的方式到达安全的避难所。这两个阶段被迭代地重复，服从终止标准，以找到优化问题的最优解。

1、算法原理

（1）初始准备阶段

鹭鹰优化算法（SBOA）方法属于基于种群的元启发式方法，其中每个鹭鹰被认为是算法种群的成员。每一只鸟在搜索空间中的位置决定了决策变量的值。因此，在SBOA方法中，Secretary Birds的位置代表了手头问题的候选解决方案。在SBOA的初始实施中，下式用于随机初始化搜索空间中的鹭鹰的位置。

其中，Xi表示第i只鹭鹰的位置，lbj和ubj分别是下限和上限，r表示0和1之间的随机数。

在鹭鹰优化算法(SBOA)中，它是一种基于种群的方法，优化从候选解的种群开始，如下式所示。这些候选解X是在给定问题的上界(ub)和下界(lb)约束下随机生成的。将目前得到的最优解近似地作为每次迭代的最优解。

X表示鹭鹰群，Xi表示鹭鹰群，Xi表示鹭鹰群，j表示鹭鹰群第j个问题变量的值，表示N个组成员的个数，而Dim表示问题变量的维度。

每个鹭鹰代表一个优化问题的候选解决方案。因此，可以根据每个鹭鹰对问题变量提出的值来评估目标函数。然后使用下式将得到的目标函数值编译成一个向量。

其中，F为目标函数值向量，Fi为第i只鹭鹰获得的目标函数值。通过比较得到的目标函数值，有效地分析相应候选解的质量，确定给定问题的最佳候选解。在最小化问题中，目标函数值最低的鹭鹰为最佳候选解，而在最大化问题中，目标函数值最高的鹭鹰为最佳候选解。由于鹭鹰的位置和目标函数的值在每次迭代中都会更新，因此有必要在每次迭代中确定最佳候选解。

（2）鹭鹰的捕猎策略(探索阶段)

鹭鹰以蛇为食时的捕猎行为通常分为三个阶段:寻找猎物、消耗猎物和攻击猎物。鹭鹰的狩猎行为如图所示。

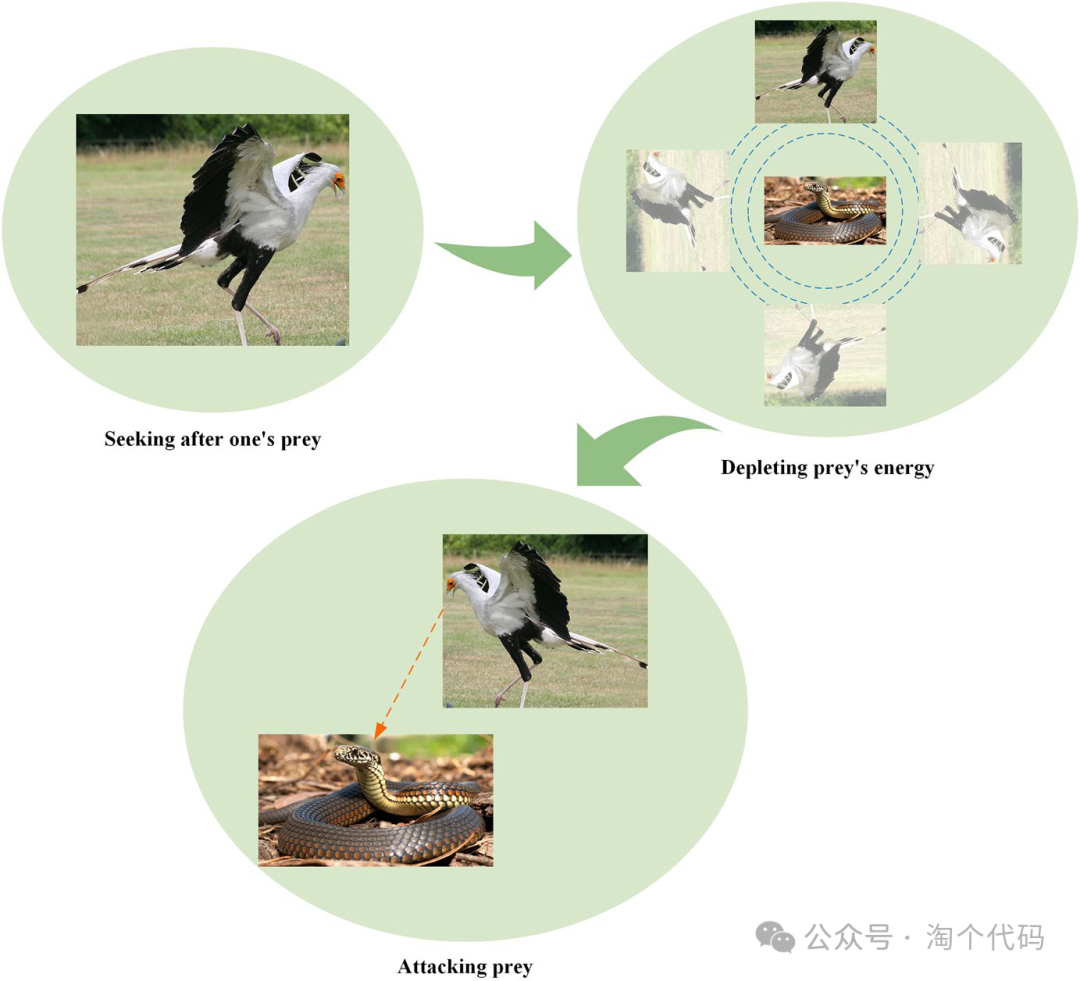
根据鹭鹰捕食阶段的生物学统计和每个阶段的持续时间，我们将整个捕食过程分为三个相等的时间间隔，分别对应鹭鹰捕食的三个阶段:寻找猎物，吃掉猎物，攻击猎物。因此，在SBOA中对各阶段建模如下:

第一阶段(寻找猎物):鹭鹰的捕猎过程通常从寻找潜在的猎物开始，尤其是蛇。鹭鹰拥有令人难以置信的敏锐视力，使它们能够迅速发现隐藏在大草原高草中的蛇。

因此，鹭鹰在寻找猎物阶段的位置更新可以用以下方程进行数学建模

式中，t表示当前迭代次数，T表示最大迭代次数， 表示第i只鹭鹰在第一阶段的新状态，xrandom_1和xrandom_2是第一阶段迭代的随机候选解。R1表示区间[0,1]中随机生成的维数为1 × Dim的数组，其中Dim为解空间的维数。 表示其第j维的值， 表示其目标函数的适应度值。

第二阶段(消耗猎物):鹭鹰发现蛇后，它采用了一种独特的捕猎方法。不像其他猛禽会立刻扑进去战斗，鹭鹰用它敏捷的步法和在蛇周围的机动。鹭鹰站在原地，从高处观察蛇的一举一动。它利用对蛇的动作的敏锐判断，盘旋、跳跃、逐渐激怒蛇，从而消耗对手的耐力。在这个阶段，我们引入布朗运动(RB)来模拟鹭鹰的随机运动。

布朗运动可以用下式进行数学建模

其中，randn(1, Dim)表示从标准正态分布中随机生成的维数为1 × Dim的数组，xbest表示当前最优值。

第三阶段(攻击猎物):当蛇筋疲力尽时，鹭鹰察觉到合适的时机，迅速采取行动，利用其强大的腿部肌肉发动攻击。因此，更新鹭鹰在攻击猎物阶段的位置可以使用以下方程进行数学建模：

其中 为非线性扰动因子

为了提高算法的优化精度，我们使用加权Levy飞行，记为“RL”。

其中Levy(Dim)表示Levy飞行分布函数。计算方法如下:

这里，s是0.01的固定常数，n是1.5的固定常数。U和v是区间[0,1]内的随机数。σ的公式如下:

这里，Γ表示伽马函数，n的值为1.5。

（3）鹭鹰的逃生策略(开发阶段)

鹭鹰的天敌是大型食肉动物。第一种策略是逃跑或快速奔跑。第二种策略是伪装，使捕食者更难发现它们。它们在面对威胁时的逃避行为如图所示。

在SBOA的设计中，假设下列两种情况中的一种以等概率发生:

在第一种策略中，当鹭鹰探测到捕食者的附近时，它们首先寻找合适的伪装环境。如果附近没有合适和安全的伪装环境，它们会选择飞行或快速奔跑逃跑。在这种情况下，我们引入一个动态扰动因子，记为 。这种动态扰动因素有助于算法在探索(寻找新的解决方案)和利用(使用已知的解决方案)之间取得平衡。

第一种逃跑策略对应的公式为

第二种逃跑策略对应的公式为

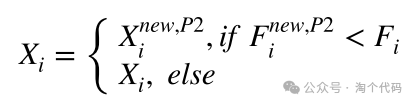
其中，C1对应环境伪装;C2对应飞或者跑，r = 0.5，R2表示从正态分布中随机生成维度为(1 × Dim)的数组，xrandom表示当前迭代的随机候选解，K表示整数1或2的随机选择，可由下式计算。

这里，rand(1,1)表示在(0,1)之间随机生成一个随机数。

综上所述，SBOA的流程图如图所示

2、伪代码流程

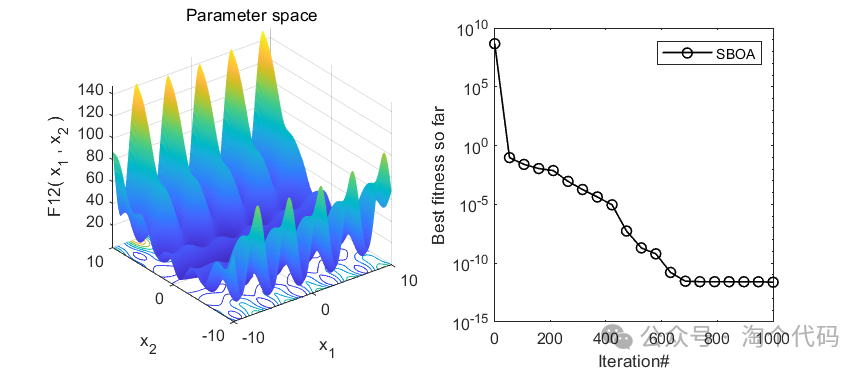
3、结果展示

4、MATLAB核心代码

%%% Secretary Bird Optimization Algorithm(SBOA)% Fu, Y., Liu, D., Chen, J. et al. Secretary bird optimization algorithm: a new metaheuristic for solving global optimization problems. Artif Intell Rev 57, 123 (2024). https://doi.org/10.1007/s10462-024-10729-y% https://doi.org/10.1007/s10462-024-10729-y  function[Best_score,Best_pos,SBOA_curve]=SBOA(N,T,lb,ub,dim,fitness)lb=ones(1,dim).*(lb);                              ub=ones(1,dim).*(ub);                             %% INITIALIZATIONfor i=1:dim    X(:,i) = lb(i)+rand(N,1).*(ub(i) - lb(i));                          endfor i =1:N    M=X(i,:);    fit(i)=fitness(M);end%% main loopfor t=1:T    CF=(1-t/T)^(2*t/T);    %% update the global best (fbest)    [best , location]=min(fit);    if t==1        Bast_P=X(location,:);                                           % Optimal location        fbest=best;                                           % The optimization objective function    elseif best<fbest        fbest=best;        Bast_P=X(location,:);    end        %% The secretary bird's predation strategy    for i=1:N        if t<T/3  % Secretary bird search prey stage           Rn=size(X,1);           X_random_1=randi([1,Rn]);           X_random_2=randi([1,Rn]);           R1=rand(1,dim);           X1=X(i,:)+(X(X_random_1,:)-X(X_random_2,:)).*R1;            X1= max(X1,lb);           X1 = min(X1,ub);        elseif t>T/3 && t<2*T/3  % Secretary bird approaching prey stage               RB=randn(1,dim);               X1=Bast_P+exp((t/T)^4)*(RB-0.5).*(Bast_P-X(i,:));               X1= max(X1,lb);               X1 = min(X1,ub);        else       % Secretary bird attacks prey stage            RL=0.5*Levy(dim);            X1=Bast_P+CF*X(i,:).*RL;            X1= max(X1,lb);            X1 = min(X1,ub);        end        f_newP1 = fitness(X1);        if f_newP1 <= fit (i)            X(i,:) = X1;            fit (i)=f_newP1;        end    end     %% Secretary Bird's escape strategy    r=rand;    k=randperm(N,1);    Xrandom=X(k,:);    for i=1:N        if r<0.5            %% C1: Secretary birds use their environment to hide from predators            RB=rand(1,dim);            X2= Bast_P+(1-t/T)*(1-t/T)*(2*RB-1).*X(i,:);% Eq.(5) S1            X2= max(X2,lb);X2 = min(X2,ub);              else            %% C2:  Secretary birds fly or run away from the predator            K=round(1+rand(1,1));            R2=rand(1,dim);            X2=X(i,:)+ R2.*(Xrandom-K.* X(i,:)); %  Eq(5) S2            X2= max(X2,lb);X2 = min(X2,ub);                     end                f_newP2 = fitness(X2); %Eq (6)        if f_newP2 <= fit (i)            X(i,:) = X2;            fit (i)=f_newP2;        end    end %    best_so_far(t)=fbest;    average(t) = mean (fit);    end Best_score=fbest;Best_pos=Bast_P;SBOA_curve=best_so_far;end%% Levy flight functionfunction o=Levy(d)beta=1.5;sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);u=randn(1,d)*sigma;v=randn(1,d);step=u./abs(v).^(1/beta);o=step;end

参考文献

[1]Fu Y, Liu D, Chen J, et al. Secretary bird optimization algorithm: a new metaheuristic for solving global optimization problems[J]. Artificial Intelligence Review, 2024, 57(5): 1-102.

完整代码获取

后台回复关键词：

TGDM900

---

点个"赞"再走吧~