张正友标定法：A Flexible New Technique for Camera Calibration-CSDN博客

本文链接：https://blog.csdn.net/wolfcsharp/article/details/92803180

本文围绕张氏标定法展开，介绍其仅需相机观察平面图案在不同方向的情况，可自由移动相机或图案，还对径向镜头畸变建模。阐述了基本方程，包括各坐标系关系、单应性矩阵等，详细说明了求解相机标定的闭式解、最大似然估计及径向镜头畸变估计等内容。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

张正友标定法：A Flexible New Technique for Camera Calibration

Abstract
MOTIVATIONS
BASIC EQUATIONS
SOLVING CAMERA CALIBRATION

Abstract

It only requires the camera to observe a planar pattern shown at a few (at least two) different orientations.
Either the camera or the planar pattern can be freely moved
Radial lens distortion is modeled
The proposed procedure consists of a closed-form solution(闭式解即解析解), followed by a nonlinear refinement based on the maximum likelihood criterion.

MOTIVATIONS

在张氏标定法被提出之前，将已有的标定方法大致分为两类：
摄影测量标定：通过观察校准对象来执行相机校准，该校准对象在3D空间中的几何形状已知且具有非常好的精度。这种方法需要昂贵的校准装置和精心设置。
自标定：在静态场景中移动摄像机，拍摄三幅图片，这种方法很简便，但是并不成熟，标定结果不可靠。
张氏标定法则使用2D度量信息，位于使用显式3D模型的摄影测量标定和使用运动刚度或等效隐式3D信息的自标定之间。

BASIC EQUATIONS

Notation

根据相机的小孔成像模型，将世界坐标系和像素坐标系写成等式(1), 关于世界坐标系、相机坐标系、图像坐标系、像素坐标系之间的空间及数学关系，请参考这篇文章。
在这里插入图片描述

其中：
s是一个任意的尺度因子。
[R t]是相机的外参矩阵，它是世界坐标系到相机坐标系之间的转换参数，世界坐标系通过旋转、平移可以转换到相机坐标系。R是旋转矩阵，t是平移矩阵。
A是相机的内参矩阵，(u₀,v₀)是图像坐标系的原点坐标在像素坐标系上的值；, alpha和beta是在像素坐标系下u轴和v轴上的尺度因子；gamma是描述两个图像轴偏斜的参数。
在这里插入图片描述

Homography between the Model Plane and Its Image

假设标定板所在的平面为世界坐标系的Z=0的平面，这是张氏标定法简化标定流程的重要一步。
在这里插入图片描述
引入单应性矩阵H：

1.单应性矩阵H大小是3 by 3的，并且是一个齐次矩阵，因为其中包含一个齐次坐标，因此存在8个未知数，至少需要8个方程才能求解.
2.根据等式(2)，当给定一对单应性对应点的时候，能够得到两个方程.
3.因此至少需要四个对应点，建立8个方程，就可以算出世界坐标系平面到像素坐标系平面的单应性矩阵H.

Constraints on the Intrinsic Parameters

给定平板模型的一幅图像，把s移到等式右边，记单应性矩阵H=[h₁ h₂ h₃]
在这里插入图片描述
这里有这样一些前提条件及其推导：
(1) lamda = 1/s
(2)A是可逆的，因此
r₁=A^-1h₁/lamda
r₂=A^-1h₂/lamda
(3)旋转矩阵是一个酉矩阵，r₁与r₂正交，因此
r₁^Tr₂=0
||r₁||=||r₂||=1，即r₁^Tr₁=r₂^Tr₂
综上，推导出上面的(3)和(4)式。
每个单应性矩阵H可以提供两个方程，而内参矩阵包括5个参数，要求解内参矩阵A，至少需要三个单应性矩阵
为了得到三个不同的单应性矩阵，我们至少调整标定板两次，即至少获得三幅棋盘格平面的图片进行标定。

SOLVING CAMERA CALIBRATION

We start with an analytical solution,followed by a nonlinear optimization technique based on the maximum-likelihood criterion. Finally, we take into account lens distortion, giving both analytical and nonlinear solutions.

Closed-Form Solution

在这里插入图片描述

如果观察到模型平面的n个图像，则通过堆叠n个这样的等式(8)，我们可以得到：

这里V是一个2n by 6的矩阵。
如果是n >=3，我们通常会得到一个唯一的解b，其定义为比例因子。
如果n=2，我们可以强加无偏约束gamma=0,即[0,1,0,0,0,0]b=0,作为(9)的附加等式,也可以解出b。
如果n = 1，我们只能求解出相机的两个内参，例如，假设u₀和v₀是已知的（比如图像坐标系原点在像素坐标系的中心），并且假设gamma=0，这样就可以求得alpha和beta。
一旦b被求解出来，我们就可以计算所有的相机内参,矩阵B可以被写成：
在这里插入图片描述
其中，lamda是一个任意大小的尺度因子，因此可以从矩阵B中唯一地提取内参。

一旦知道内参矩阵A，就可以容易地计算外部参数。根据等式(2)，我们有
r₁=A^-1h₁/lamda
r₂=A^-1h₂/lamda
r₃=r₁×r₂
t=A^-1h₃/lamda
其中，lamda=||A^-1h₁||=||A^-1h₂||

Maximum-Likelihood Estimation

上述的推导结果是基于理想情况下的解，但由于可能存在高斯噪声，所以使用MLE进行优化。设我们采集了n副包含棋盘格的图像进行标定，每个图像里有棋盘格角点m个。令第i副图像上世界坐标系下的角点M_ij在上述计算得到的内参A，外参R和t下，在像素坐标系下的投影点为：
在这里插入图片描述
其中R_i和t_i是第i副图对应的旋转矩阵和平移向量。则角点m_ij的概率密度函数为：

构造似然函数：

MLE使得目标函数L取得最大值，等价于最小化如下函数：

最小化式(10)是一个非线性最小化问题，可以利用LM算法求解，初始值设置为上面的不精确的解，然后逐步迭代找到最优解。关于LM算法，请参考我的另一篇博客LM(Levenberg–Marquardt)算法原理及其python自定义实现

Radial lens distortion estimation

摄像机通常具有显性的镜头失真，尤其是径向畸变。张氏标定法只关注了影响最大的径向畸变。去除高阶，镜像畸变的数学模型可以用如下的等式描述:
在这里插入图片描述
其中(x,y)是理想的无畸变的归一化图像坐标系坐标，(x_hat,y_hat)是畸变后的归一化图像坐标系坐标，k₁和k₂表示前两阶径向畸变系数。

而径向畸变的中心和相机的主心是在相同的位置，因此有：
在这里插入图片描述
其中，(u,v)是理想的无畸变像素坐标系坐标，(u_hat,v_hat)是畸变后的像素坐标系坐标，(u₀,v₀)是相机的主点。
假设gamma=0，则有：

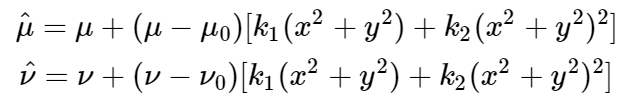
写成矩阵形式：

上面的等式是从一幅图像上的一个点取得，仍然设有n幅图像，每幅图像上有m个点，则将得到的所有等式组合起来，可以得到2mn个等式，将其记成矩阵形式：
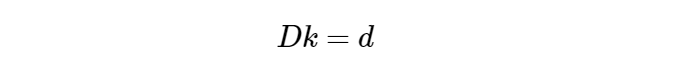
在这里插入图片描述
求解出畸变参数k：

同样使用MLE，用LM算法最小化如下目标函数：

得到畸变参数k1,k2后，可以先将图像进行去畸变处理，然后用去畸变后的图像坐标估计相机的内参数，继而算出外参数。