题目信息如下:
1、题目地址为:https://leetcode.com/problems/largest-rectangle-in-histogram/
2、题目意思为:
给定一个非负数组height,代表了矩形的高度(其中矩形宽度为1),求在其中能找出最大的矩形面积。
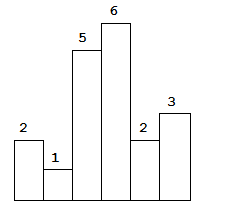
3、给的例子为: height = [2,1,5,6,2,3]. 输出为:10.示意图如下
那么下面为正文,讲讲算法的依据(以上面的例子为例):
1、第一个2就没什么讲的了,面积必然为2。
2、当指针指向height[1]的时候,面积有1(也就是自身)和2(如下图)两种可能。

3、当指针指向height[2]的时候,如下图所示,有3种面积可能。
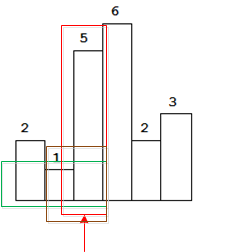
4、当指针指向height[3]的时候,如下图,有4中可能(图中少画了h[1]-[3]的组合)
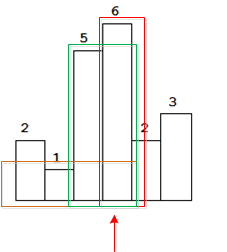
对比3、4我发现一个有用的规律:
h[2]的所有面积情况下,都可以加上h[3]所对应的面积。
也就是,如果指针所在的高度(如h[2]=5)的后面有和自己更高的或者相等的高度(如h[3]=6),那么最大的面积就不可能是指针所在的高度和前面的组合。
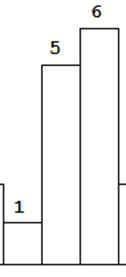
用下面的图片描述上面的规律,更加贴切。如果要在下图中找最大的面积,必然有高度为6的参与。
另起一段:
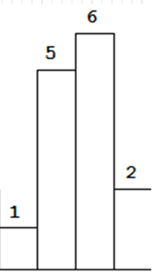
遇到上面这样的排列,我们会怎么组合?
看了上面的介绍,你肯定会说,直接1 5 6组合中找最大的,接下来再5 6 2中找最大的面积,最后再看1*4的面积。
好像有点问题,比如1 5 6 组合中,可能存在1 1 1这样的矩阵,那么为什么不直接讲矩阵拉到2上,也就是说1 1 1 1 = 4的面积哇?
所以总结下我们可以得到下图这样的组合方法:

指针从1开始向后移动,不停的记录信息,直到指针指向2,由于2<6,此时开始计算前面的高度5、6的面积组合,为啥不计算1呢,由于1<2,如果最大面积组合中包含1,那么必然包含2,如上图的红框。最后我们知道,1后面高度都是大于2,那么 面积=(2的下标-1的下标-1)*2的高度。
最后附上代码:
public int largestRectangleArea(int[] height) {
if(height == null || height.length == 0) return 0;
int len = height.length;
Stack<Integer> stack = new Stack<Integer>();
int max = 0;
for(int i=0; i<len; i++){
if(stack.empty() || height[i] >= height[stack.peek()]){//将大于等于栈顶的height入栈,那么中是一个不减序列
stack.push(i);
}
else{//height 小于栈顶的高度
int left = 0;
while(!stack.empty() && height[i] < height[stack.peek()]){//直到栈顶的高度小于当前高度
left = stack.pop();
int cur = height[left] * (stack.empty()?i:i-stack.peek()-1);//入栈是递增,出栈是递减,也就是当前序列高度*出栈了的个数,就是当前的面积
if(max < cur){
max = cur;
}
}
stack.push(i);
}
}
int left = 0;
while(!stack.empty()){//这里用来处理比如[1 2 3 4 5 6 7 8]这样的递增序列或递增子序列
left = stack.pop();
int cur = height[left] * (stack.empty()?len:len-stack.peek()-1);
if(max < cur)
max = cur;
}
return max;
}
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








