数据结构考研:大O表示法最浅显易懂且详细深入的解释及与小o表示法的区别(十分钟必懂)

大O表示法的背景

作为软件工程专业的学生，在我们学习数据结构的时候，总是会碰见对各种算法时间复杂度和空间复杂度的大O表示法的描述。我们只是将信将疑的用着，并不知道大O表示法的准确含义，今天博主李同学在查阅各方资料后进行详细地讲解。

大O表示法的定义

根据Big O notation(大O表示法)维基百科的描述：

大O表示法的字母O是函数的增长率，也被称为函数的阶数，即字母O代表Order(阶数)。用大O符号描述函数通常只提供函数增长率的一个上界。
设f是实或复值函数，g是实值函数，它们都定义在实正数的无界子集上，使得g(x)对于所有足够大的x都为正数，那么我们称：当x趋向于无穷大时，f(x)=O(g(x))。
另外，对于所有足够大的x值，f(x)的绝对值最多是g(x)的正常数倍。即f(x) = O(g(x))有且仅有一个实数M和一个实数x₀使得：对于所有x≥x₀的x，|f(x)|≤Mg·(x)恒成立。

在典型的用法中，O符号是渐近的，也就是说，它指的是非常大的x。因此，可以应用以下简化规则：如果f(x)是几个项的和，如果有一个增长率最大的项，它可以保留，其他项都可以省略。
如果f(x)是几个因子的乘积，任何常数(乘积中不依赖于x的项)都可以省略。
例如，让f(x) = 6x⁴ - 2x³ + 5，假设我们想要简化这个函数，用大O表示法来描述x趋于无穷时的增长率。这个函数是三项的和：6x⁴, 2x³和5。在这三项中，增长率最高的是指数最大的x，即6x⁴。现在我们可以应用第二个规则：6x⁴是6和x⁴的乘积，其中第一个因子不依赖于x，省略这个因子就得到了简化形式x⁴。因此，我们说f(x)是(x⁴)的Big O。数学上，我们可以写成f(x) = O(x⁴)可以用形式定义来确认这个计算：令f(x) = 6x⁴-2x³ + 5, g(x) = x⁴。应用一个正式定义，f(x) = O(x⁴)等于它的展开式|f(x)|≤MX⁴，其中M是一个常数。对于某些合适的x0和M以及所有的x >x₀。为了证明这一点，令x0 = 1, M = 13。然后，对于所有的x > x₀：

因此，我们说：|6x⁴-2x³ + 5|≤13x⁴
而这个表达式用大O表示法，可写成：(6x⁴-2x³ + 5)=O(x⁴)

大O表示法与小o表示法的区别

如果你上过高等数学的课程，你一定对小o表示法不陌生，下面是高阶无穷小，也就是小o表示法的定义：

设为a_n和b_n为两个序列的数，而且都是n趋近于无穷时的无穷小量。虽然它们在n趋近于无穷时都趋于零，但趋于零的速度是有区别的。
可以用如下方式比较它们的速度：
若对于任意正实数c>0，存在正整数N，在k>N时，使得a_k<c·b_k总是成立，则称：当n趋近于无穷时，a_n=o(b_n)，即a_n是b_n的高阶无穷小。
在上述定义中，也可以说无穷小量a_n的阶要比b_n的要高，或者说a_n比b_n更快地趋于零，尽管在此时“阶”或者“速度”本身其实都没有明确的定义。

通过上述我对小o表示法的讲解后，我们再看看维基百科中对大O表示法与小o表示法区别的描述：

符号	名字	描述	公式定义
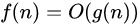	大O表示法	f渐近地以g为界
	小o表示法	f渐近地被g控制

由这个对比表格，我们可以清楚地知道：
大O表示法f(n)=O(g(n))中的f(n)是g(n)的等阶无穷大或者是同阶无穷大。
小O表示法f(n)=o(g(n))中的f(n)是g(n)的高阶无穷小。