POJ 1179 Polygon（区间DP）

题目链接：http://poj.org/problem?id=1179

Description

Polygon is a game for one player that starts on a polygon with N vertices, like the one in Figure 1, where N=4. Each vertex is labelled with an integer and each edge is labelled with either the symbol + (addition) or the symbol * (product). The edges are numbered from 1 to N.

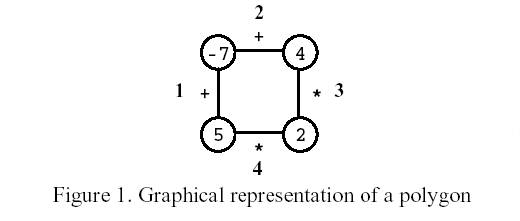
On the first move, one of the edges is removed. Subsequent moves involve the following steps:
1. pick an edge E and the two vertices V1 and V2 that are linked by E; and
2. replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2.
The game ends when there are no more edges, and its score is the label of the single vertex remaining.

Consider the polygon of Figure 1. The player started by removing edge 3. After that, the player picked edge 1, then edge 4, and, finally, edge 2. The score is 0.

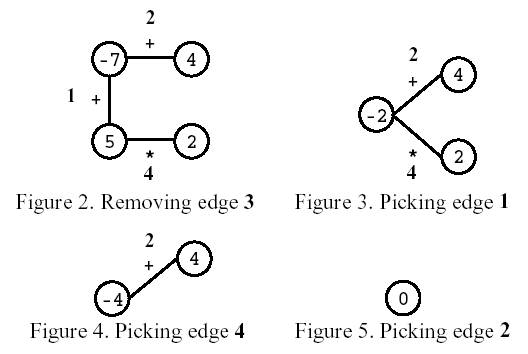
Write a program that, given a polygon, computes the highest possible score and lists all the edges that, if removed on the first move, can lead to a game with that score.

Input

Your program is to read from standard input. The input describes a polygon with N vertices. It contains two lines. On the first line is the number N. The second line contains the labels of edges 1, …, N, interleaved with the vertices’ labels (first that of the vertex between edges 1 and 2, then that of the vertex between edges 2 and 3, and so on, until that of the vertex between edges N and 1), all separated by one space. An edge label is either the letter t (representing +) or the letter x (representing *).

3 <= N <= 50
For any sequence of moves, vertex labels are in the range [-32768,32767].

Output

Your program is to write to standard output. On the first line your program must write the highest score one can get for the input polygon. On the second line it must write the list of all edges that, if removed on the first move, can lead to a game with that score. Edges must be written in increasing order, separated by one space.

Sample Input

4
t -7 t 4 x 2 x 5

Sample Output

33
1 2

Source

IOI 1998

解题思路

这道题的题意大致是对于n个点的环先删除一个点后，根据连线的运算符逐渐合并各个点，最后求最大的结果可能是多少。一道经典的区间DP题，有几个点需要注意一下：

1. 需要枚举最开始删除的是哪条边
2. 由于一开始是个环，删边后可能从中间断开，导致区间不连续，无法使用区间DP。解决方法是将原始数组复制一倍，这样就能保证能够使用区间DP。
3. 由于元素可能存在负值，负负相乘得正后可能得到的结果更大。所以在维护结果的时候，既要维护最大值，也要维护最小值。

AC代码

#include<bits/stdc++.h>
//#define TEST
using namespace std;
#define INF 400000
int n,ans;
char op[105];
int num[105],ma[105][105],mi[105][105];
vector<int> lt;

int mmax(int s,int k,int t,char z)
{
    if(z=='t')
        return ma[s][k-1]+ma[k][t];
    else
        return max(ma[s][k-1]*ma[k][t],mi[s][k-1]*mi[k][t]);
}

int mmin(int s,int k,int t,char z)
{
    if(z=='t')
        return mi[s][k-1]+mi[k][t];
    else
        return min(ma[s][k-1]*ma[k][t],mi[s][k-1]*mi[k][t]);
}

int main()
{
    scanf("%d\n",&n);
    for(int i=0;i<n;i++){
        scanf("%c %d%*c",&op[i],&num[i]);
        op[i+n]=op[i];
        num[i+n]=num[i];    // 增加一倍长度
    }
    for(int i=0;i<2*n;i++){
        for(int j=0;j<2*n;j++){
            ma[i][j]=-INF;
            mi[i][j]=INF;
        }
    }
    for(int i=0;i<(n<<1);i++){
        ma[i][i]=mi[i][i]=num[i];
    }
        #ifdef TEST
    for(int i=0;i<2*n;i++){
        for(int j=0;j<2*n;j++){
            cout<<ma[i][j]<<' ';
        }
        cout<<endl;
    }
    #endif // TEST
    for(int d=1;d<=n;d++){
        for(int s=0;s<2*n-d+1;s++){
            int t=s+d-1;
            for(int k=s+1;k<=t;k++){
                ma[s][t]=max(ma[s][t],mmax(s,k,t,op[k]));
                mi[s][t]=min(mi[s][t],mmin(s,k,t,op[k]));
            }
        }
    }
    #ifdef TEST
    for(int i=0;i<2*n;i++){
        for(int j=0;j<2*n;j++){
            cout<<ma[i][j]<<' ';
        }
        cout<<endl;
    }
    #endif // TEST
    ans=-INF;
    lt.clear();
    for(int i=0;i<n;i++){
        if(ma[i][i+n-1]>ans){
            ans=ma[i][i+n-1];
            lt.clear();
            lt.push_back(i+1);
        }
        else if(ma[i][i+n-1]==ans){
            lt.push_back(i+1);
        }
    }
    printf("%d\n",ans);
    printf("%d",lt[0]);
    for(int i=1;i<lt.size();i++){
        printf(" %d",lt[i]);
    }
    printf("\n");
    return 0;
}