变步长梯形法与龙贝格算法

1. 变步长梯形法

提出背景：
复化求积公式虽然能提高精度，但需要给出步长，步长精度太大则精度低，步长太小则计算量大，难以找到一个合适的步长（划分成的小区间的个数）

算法描述

1.对所有已存在的子区间进行二分化，区间数由n变为2n
2.利用区间数为n时的积分值Tn以及新增的节点（即原来各子区间的中点）递推出区间数为2n时的积分值T2n
3.利用两次计算结果的差来估计误差，直到满足精度
公式如下：

流程图

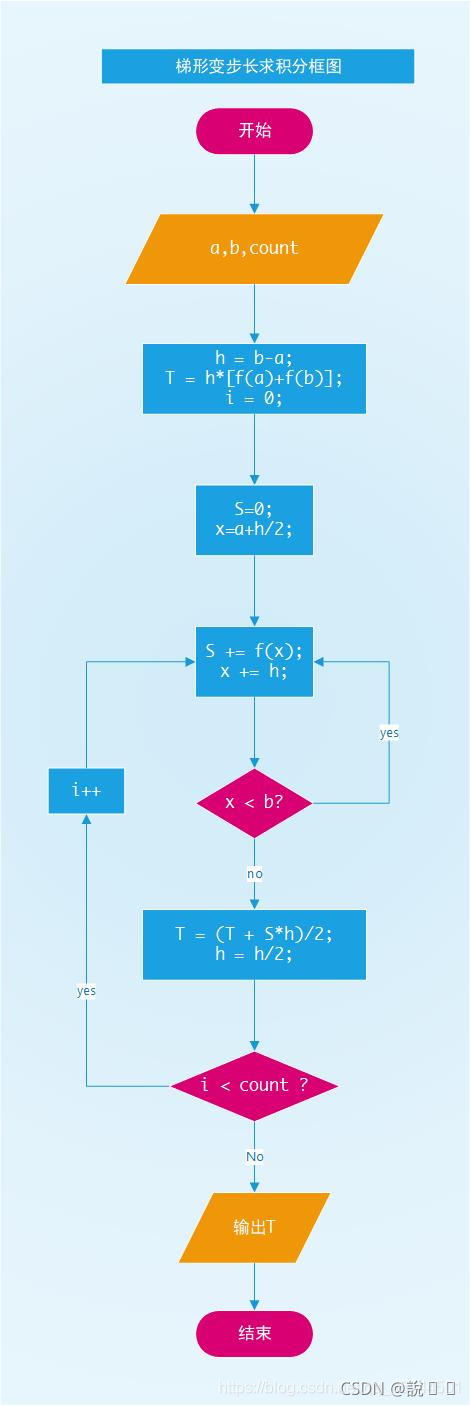
代码实现

/**
 *@name Variable_step：利用变步长梯形公式求积
 *@param1 down：积分下限
 *@param2 upper：积分上限
 *@param3 limit_error：误差限
**/
void Variable_step(double down,double upper,double limit_error)
{
	Tn[0]=(function(down)+function(upper))/2;

	double h;		//定义小区间的长度
	double n=0.5;		//定义划分的区间数
	double S=0;		//新增和

	//注意每次区间二分，不是自加
	for (int i=0;i<19;i++)
	{
		//从前先后推 Tn[0]->Tn[1] 每次对区间进行二分
		n=n*2;		
		//计算小区间的长度
		h=(upper-down)/n;	

		S=0;
		//计算小区间内所有中点的函数和 
		for (int j=0;j<n;j++)
		{
			S+=function(down+j*h+h/2);
		}

		//迭代到下一项
		Tn[i+1]=Tn[i]/2+(h/2)*S;

		//如果检测到误差小于限制，则直接输出
		if(abs(Tn[i+1]-Tn[i])/3<limit_error)
			break;
	}
}

2. 龙贝格算法

提出背景：
梯形公式收敛阶为2阶（余项为h的2次），利用
变步长梯形公式时收敛速度较慢，故提出了龙贝格算法加速收敛

算法描述

1.对得到的梯形序列Tn（1次代数精度）的相邻两项进行线性组合，即可得到抛物序列Sn（3次代数精度）
2.对抛物序列Sn的相邻两项进行线性组合，可得到柯斯序列Cn（5次代数精度）
3.对柯斯序列Cn的相邻两项进行线性组合，可得到龙贝格序列（7次代数精度）
示意图：

公式：

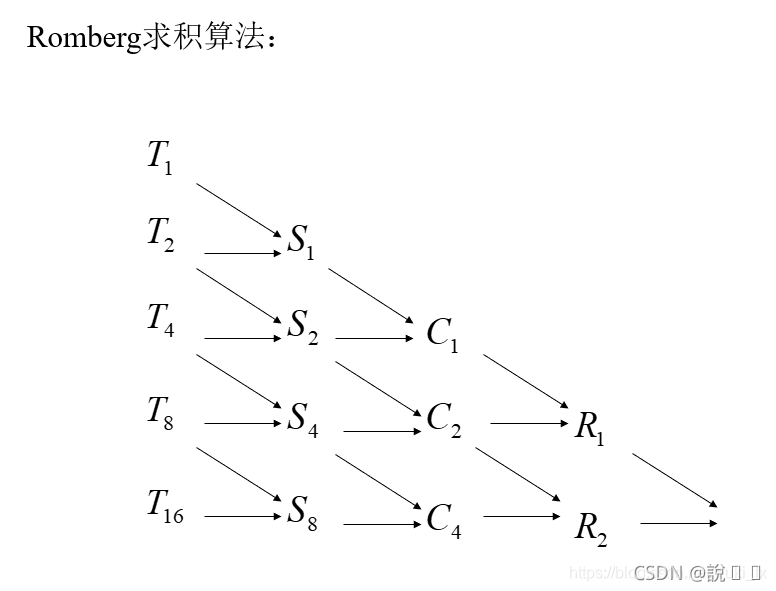
例子

代码实现

注意：
1.integral_table[10][4]为龙贝格积分表，从第0列到第3列分别为Tn，Sn，Cn，Rn
2.Tn（integral_table[i][0]）通过变步长梯形法求得
3.Sn，Cn，Rn由前一列的同行以及上一行的项进行线性组合得到

/**
 *@name Romberg_arithmetic：利用龙贝格算法建立积分结果表
 *@param1 down：积分下限
 *@param2 upper：积分上限
**/
void Romberg_arithmetic(double down,double upper)
{
	double S=0;
	double n=0.5;
	double h=(upper-down);
	integral_table[0][0]=(function(down)+function(upper))*(h/2);
	//计算顺序	外循环由列开始迭代：1列 2列 3列（其中第0列由变步长梯形法求得）
	//					内循环行迭代

	//变步长梯形法求第0列 Tn
	for (int i=0;i<10;i++)
	{
		n=n*2;
		h=(upper-down)/n;
		
		S=0;
		for (int j=0;j<n;j++)
		{
			S+=function(down+j*h+h/2);
		}

		integral_table[i+1][0]=integral_table[i][0]/2+S*(h/2);
	}

	//计算Sn Cn Rn
	for (int i=1;i<4;i++)
	{
		for(int j=i;j<10;j++)
		{
			//利用龙贝格求积公式
			integral_table[j][i]=(pow(4.0,i)*integral_table[j][i-1]-integral_table[j-1][i-1])/(pow(4.0,i)-1);
		}
	}
}

python代码实现

# -*- coding: utf-8 -*-
"""
Created on Sat Oct 30 09:55:51 2021

@author: Administrator
"""

import numpy as np


def f(x):
    '''
    定义f(x)
    :param x: 需要计算的函数值
    :return: 返回sinx/x 的值
    '''
    if x == 0:
        x = 1e-20
    return np.sin(x) / x


def romberg(a, b, e):
    '''
    使用龙贝格算法，计算sinx/x在(a,b)之间的差距
    :param a: 积分下限
    :param b: 积分上限
    :param e: 误差极限
    :return:
    '''
    h = b - a
    # n为划分的区间数
    n = 1
    # k表示行数
    k = 0
    # T为龙贝格积分表,定义一个20*20 的矩阵。矩阵的值为0
    T = np.zeros((15, 15))
    # T_0=就等于梯形面积
    T[0][0] = (f(a) + f(b)) * (h / 2)
    # 错误率
    err = 10
    while err >= e:
        # S表示梯形的面积
        S = 0
        # 行数+1
        k += 1
        # h为[a,b]这段区间中，被分成n分，每一份的长度。
        # 假设a=5,b=7,n为5分,h为[5,7]这段区间，被分成了5份，每份0.4,h=0.4
        # h = (b - a) /n   h=h/2,因为后面n=n*2
        h = h / 2
        # 变步长梯形法求第0列 Tn,n越大
        for i in range(1, n+1):
            S = S + f(a + (2 * i - 1) * h)

        # T_2n=1/2T_n+h/2*积分和
        # T[k][0]放置的是T_{2k}的值，第0列,T_0,T_2,T_4,T_8
        T[k][0] = T[k - 1][0] / 2 + h * S
        # 计算S_n,C_n,R_n
        for m in range(1, k + 1):
            T[k][m] = T[k][m - 1] + (T[k][m - 1] - T[k - 1][m - 1]) / (4 ** m - 1)

        # 为了增加梯形的精度，所以增加划分区间的
        n = n * 2
        # 计算误差率
        err = abs(T[k][k] - T[k - 1][k - 1])

    np.savetxt("result.txt", T, delimiter=',', fmt="%.10f")


# 初始化初始值，a,b,e
# a表示积分下限
# b表示积分上限
# e表示误差限
a = 0
b = 1
e = 1e-10
romberg(a, b, e)