题意:
求有多少个数对(x,y),满足a≤x≤b,c≤y≤d,且gcd(x,y) = k;
1≤a≤b≤50000,1≤c≤d≤50000
1≤n≤50000,1≤k≤50000
题解:
首先可以把询问拆成四个,然后容斥一下就是答案
问题转化成求gcd(x,y)=k,1<=x<=n,1<=y<=m的(x,y)对数
令f(x)为满足条件的gcd(x,y)=x的(x,y)对数;
令F(x)为满足条件的x|gcd(x,y)的(x,y)对数;
那么显然有
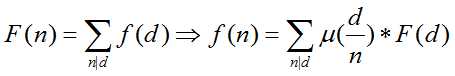
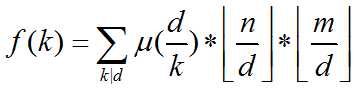
有了这东西
枚举i=d/k,即
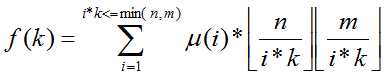
就可以O(n)搞出这道题了
然而暴力枚i不可取,多组数据教做人
发现
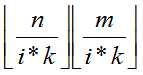
最多有√n级别的取值
那么直接枚举每个取值,对莫比乌斯函数求前缀和
然后用这个取值乘这一段的函数和,累加就是答案了
复杂度O(n+q√n);
这篇文章的排版是不是很魔性2333,其实本来是我ppt里的东西
强行粘出来弄几篇题解吧233
求有多少个数对(x,y),满足a≤x≤b,c≤y≤d,且gcd(x,y) = k;
1≤a≤b≤50000,1≤c≤d≤50000
1≤n≤50000,1≤k≤50000
题解:
首先可以把询问拆成四个,然后容斥一下就是答案
问题转化成求gcd(x,y)=k,1<=x<=n,1<=y<=m的(x,y)对数
令f(x)为满足条件的gcd(x,y)=x的(x,y)对数;
令F(x)为满足条件的x|gcd(x,y)的(x,y)对数;
那么显然有
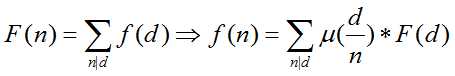
而又因为
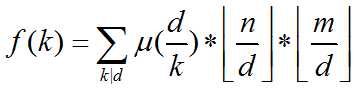
有了这东西
枚举i=d/k,即
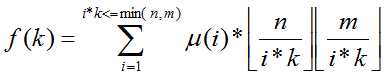
就可以O(n)搞出这道题了
然而暴力枚i不可取,多组数据教做人
发现
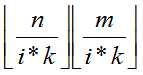
最多有√n级别的取值
那么直接枚举每个取值,对莫比乌斯函数求前缀和
然后用这个取值乘这一段的函数和,累加就是答案了
复杂度O(n+q√n);
这篇文章的排版是不是很魔性2333,其实本来是我ppt里的东西
强行粘出来弄几篇题解吧233
代码:
#include<stdio.h>
#include<string.h>
#include<algorithm>
#define N 51000
using namespace std;
typedef long long ll;
ll pri[N],tot;
ll miu[N],sum[N];
bool vis[N];
void init()
{
miu[1]=1,sum[1]=1;
for(ll i=2;i<N;i++)
{
if(!vis[i])
{
pri[++tot]=i;
miu[i]=-1;
}
for(ll j=1;j<=tot&&i*pri[j]<N;j++)
{
vis[i*pri[j]]=1;
if(i%pri[j]==0)
{
miu[i*pri[j]]=0;
break;
}
miu[i*pri[j]]=-miu[i];
}
sum[i]=sum[i-1]+miu[i];
}
}
ll mobius(ll n,ll m,ll k)
{
ll ret=0,i,j,last;
if(n>m) swap(n,m);
for(i=1;i*k<=n;i=last+1)
{
last=min(n/((n/(i*k))*k),m/(m/((i*k))*k));
ret+=(n/(i*k))*(m/(i*k))*(sum[last]-sum[i-1]);
}
return ret;
}
int main()
{
ll cs,T,a,b,c,d,k,i,j;
init();
scanf("%lld",&T);
for(cs=1;cs<=T;cs++)
{
scanf("%lld%lld%lld%lld%lld",&a,&b,&c,&d,&k);
printf("%lld\n",mobius(b,d,k)-mobius(a-1,d,k)-mobius(c-1,b,k)+mobius(a-1,c-1,k));
}
return 0;
}











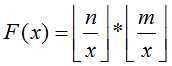














 123
123

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








