HNU 编译系统 作业2（1）

题目1

（1）找出下图中所示的 NFA 中所有标号为 aabb 的路径。这个 NFA 接受 aabb 吗？

所有标号为 aabb 的路径：0 -> 1 -> 2 -> 3
因为有1条标号为 aabb 的路径，所以这个 NFA 接受 aabb 。

（2）对于下图的 NFA，重复练习（1）。

记号定义（精确说明每段都包含哪些符号）
先定义若干“路径块”：

• Ae:(e→ε(e+1)mod  4→ε(e+2)mod  4→ε(e+3)mod  4→εe),e∈{0,1,2,3}A_e:(e \xrightarrow{\varepsilon} (e + 1)\mod 4 \xrightarrow{\varepsilon} (e + 2)\mod 4 \xrightarrow{\varepsilon} (e + 3)\mod 4 \xrightarrow{\varepsilon} e),e \in \{0,1,2,3\}Ae​:(eε​(e+1)mod4ε​(e+2)mod4ε​(e+3)mod4ε​e),e∈{0,1,2,3}
  —— 一个只含 ε 的完整环，从 e 回到 e（可重复任意次）。
• $B_{u\to v}:(u\stackrel{\epsilon }{\to }v)$
  —— 一个只含 ε 的从 u 到 v 的串。
• $C_0:(0\stackrel{a}{\to }1)$
  —— 从 0 出发消耗一个 a。
• $C_3:(3\stackrel{a}{\to }0)$
  —— 从 3 出发消耗一个 a。
• $D_1:(1\stackrel{b}{\to }2)$
  —— 从 1 出发消耗一个 b。
• $D_2:(2\stackrel{b}{\to }3)$
  —— 从 2 出发消耗一个 b。
  说明：
  上面这些块可以在必要时通过额外的 A 或 B（即插入若干 ε 串或 ε 环）在任意位置重复或衔接，从而表示“空串循环的可能”。
  形式化的路径集合
  字符串 aabb 必须顺序消耗 4 个带符号的边：第 1 个 a、第 2 个 a、第 1 个 b、第 2 个 b。
  对每一位有两种选择（第 i 个 a 可以用$C_0$或$C_3$，第 j 个 b 可以用$D_1$或$D_2$）。
  在任意两段消耗块之间都可以插入任意次的 ε 环（用$A_e$表示）并用合适的 ε 串连接（用$B_{u\to v}$表示）。
  因此，所有接受 aabb 的路径可写成如下形式的集合：
  P={Ae1p0Bu1→v1 X1 Ae2p1Bu2→v2 X2 Ae3p2Bu3→v3 Y1 Ae4p3Bu4→v4 Y2 Ae5p4Bu5→v5}p0,p1,p2,p3,p4∈N, X1,X2∈{C0,C3}, Y1,Y2∈{D1,D2}对每个 Bui→vi 的取值分类讨论：Bu1→v1:u=0,{v=0,X1=C0;v=3,X1=C3.Bu2→v2:u={1,X1=C0;0,X1=C3;v={0,X2=C0;3,X2=C3.Bu3→v3:u={1,X2=C0;0,X2=C3;v={1,Y1=D1;2,Y1=D2.Bu4→v4:u={2,Y1=D1;3,Y1=D2;v={1,Y2=D1;2,Y2=D2.Bu5→v5:u={2,Y2=D1;3,Y2=D2;v=3. \begin{aligned} &\mathcal{P} = \left\{ A_{e_1}^{p_0} B_{u_1 \xrightarrow{} v_1}\, X_1\, A_{e_2}^{p_1} B_{u_2 \xrightarrow{} v_2}\, X_2\, A_{e_3}^{p_2} B_{u_3 \xrightarrow{} v_3}\, Y_1\, A_{e_4}^{p_3} B_{u_4 \xrightarrow{} v_4}\, Y_2\, A_{e_5}^{p_4} B_{u_5 \xrightarrow{} v_5} \right\}\\ &p_0,p_1,p_2,p_3,p_4 \in \mathbb{N},\ X_1,X_2 \in \{C_0, C_3\},\ Y_1,Y_2 \in \{D_1, D_2\}\\ &\text{对每个 } B_{u_i \xrightarrow{} v_i} \text{ 的取值分类讨论：}\\ &B_{u_1 \xrightarrow{} v_1}:\quad u = 0, \quad \begin{cases} v = 0, & X_1 = C_0;\\ v = 3, & X_1 = C_3. \end{cases} \\[6pt] &B_{u_2 \xrightarrow{} v_2}:\quad u = \begin{cases} 1, & X_1 = C_0;\\ 0, & X_1 = C_3; \end{cases} \quad v = \begin{cases} 0, & X_2 = C_0;\\ 3, & X_2 = C_3. \end{cases} \\[6pt] &B_{u_3 \xrightarrow{} v_3}:\quad u = \begin{cases} 1, & X_2 = C_0;\\ 0, & X_2 = C_3; \end{cases} \quad v = \begin{cases} 1, & Y_1 = D_1;\\ 2, & Y_1 = D_2. \end{cases} \\[6pt] &B_{u_4 \xrightarrow{} v_4}:\quad u = \begin{cases} 2, & Y_1 = D_1;\\ 3, & Y_1 = D_2; \end{cases} \quad v = \begin{cases} 1, & Y_2 = D_1;\\ 2, & Y_2 = D_2. \end{cases} \\[6pt] &B_{u_5 \xrightarrow{} v_5}:\quad u = \begin{cases} 2, & Y_2 = D_1;\\ 3, & Y_2 = D_2; \end{cases} \quad v = 3. \end{aligned} ​P={Ae1​p0​​Bu1​​v1​​X1​Ae2​p1​​Bu2​​v2​​X2​Ae3​p2​​Bu3​​v3​​Y1​Ae4​p3​​Bu4​​v4​​Y2​Ae5​p4​​Bu5​​v5​​}p0​,p1​,p2​,p3​,p4​∈N, X1​,X2​∈{C0​,C3​}, Y1​,Y2​∈{D1​,D2​}对每个 Bui​​vi​​ 的取值分类讨论：Bu1​​v1​​:u=0,{v=0,v=3,​X1​=C0​;X1​=C3​.​Bu2​​v2​​:u={1,0,​X1​=C0​;X1​=C3​;​v={0,3,​X2​=C0​;X2​=C3​.​Bu3​​v3​​:u={1,0,​X2​=C0​;X2​=C3​;​v={1,2,​Y1​=D1​;Y1​=D2​.​Bu4​​v4​​:u={2,3,​Y1​=D1​;Y1​=D2​;​v={1,2,​Y2​=D1​;Y2​=D2​.​Bu5​​v5​​:u={2,3,​Y2​=D1​;Y2​=D2​;​v=3.​
  这里每一项的含义是：
• $(A^{p_i})$：表示在该位置插入$p_i$次完整的 ε 环（允许$p_i=0$表示不插入）；
• $(X_1,X_2)$：表示前两个 a 的选择：可以是 $C_0$（从 0 读 a）或 $C_3$（从 3 读 a）；
• $(Y_1,Y_2)$：表示后两个 b 的选择：可以是 $D_1$（从 1 读 b）或 $D_2$（从 2 读 b）。
  因为有标号为 aabb 的路径，所以这个 NFA 接受 aabb 。

（3）将上面两个图的NFA转为DFA。
对于图1：
初始状态：{s0}:q0{q0}→a{s0,s1}:q1{q0}→b{s0}:q0{q1}→a{s0,s1}→ε{s0,s1,s2}:q2{q1}→b{s0,s1}:q1{q2}→a{s0,s1,s2}:q2{q2}→b{s0,s1,s2,s3}:q3{q3}→a{s0,s1,s2}:q2{q3}→b{s0,s1,s2,s3}:q3 \begin{aligned} &初始状态：\{s_0\}:q_0\\ &\{q_0\}\xrightarrow{a} \{s_0, s_1\} :q_1\\ &\{q_0\}\xrightarrow{b} \{s_0\} :q_0\\ &\{q_1\}\xrightarrow{a} \{s_0, s_1\} \xrightarrow{ε}\{s_0, s_1, s_2\} :q_2\\ &\{q_1\}\xrightarrow{b} \{s_0, s_1\} :q_1\\ &\{q_2\}\xrightarrow{a} \{s_0, s_1, s_2\} :q_2\\ &\{q_2\}\xrightarrow{b} \{s_0, s_1, s_2, s_3\} :q_3\\ &\{q_3\}\xrightarrow{a} \{s_0, s_1, s_2\} :q_2\\ &\{q_3\}\xrightarrow{b} \{s_0, s_1, s_2, s_3\} :q_3\\ \end{aligned} ​初始状态：{s0​}:q0​{q0​}a​{s0​,s1​}:q1​{q0​}b​{s0​}:q0​{q1​}a​{s0​,s1​}ε​{s0​,s1​,s2​}:q2​{q1​}b​{s0​,s1​}:q1​{q2​}a​{s0​,s1​,s2​}:q2​{q2​}b​{s0​,s1​,s2​,s3​}:q3​{q3​}a​{s0​,s1​,s2​}:q2​{q3​}b​{s0​,s1​,s2​,s3​}:q3​​
得到的DFA为：

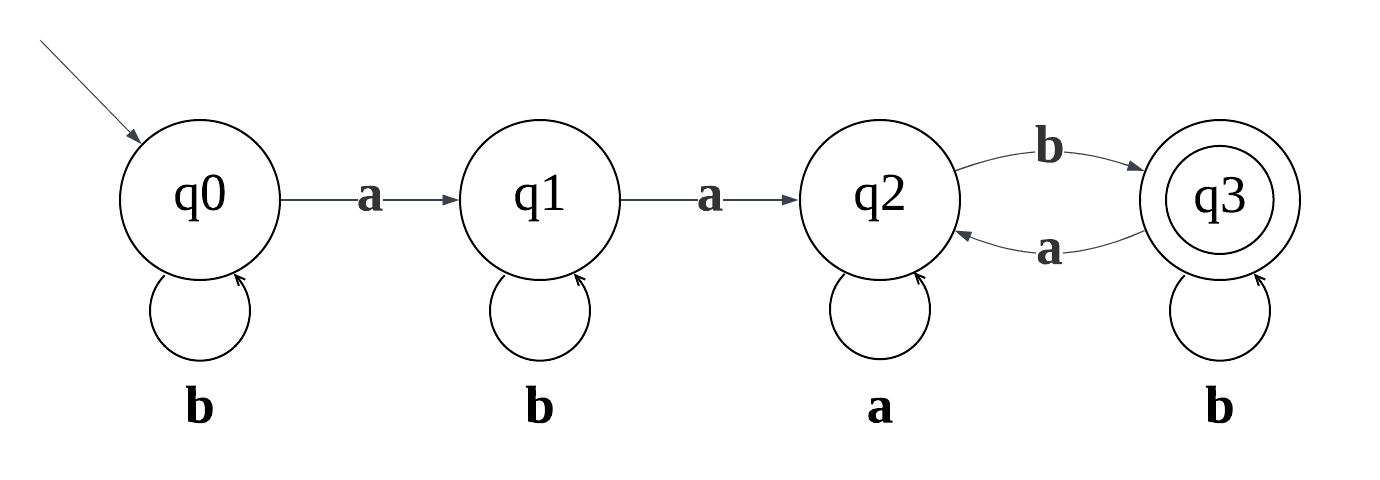
对于图2：
初始状态：{s0}:q0{s0}→a{s1}→ε{s0,s1,s2,s3}:q0{s0}→ε{s0,s1,s2,s3}:q0{s1}→b{s2}→ε{s0,s1,s2,s3}:q0{s2}→b{s3}→ε{s0,s1,s2,s3}:q0{s3}→a{s0}→ε{s0,s1,s2,s3}:q0 \begin{aligned} &初始状态：\{s_0\}:q_0\\ &\{s_0\}\xrightarrow{a}\{s_1\}\xrightarrow{ε}\{s_0, s_1, s_2, s_3\} :q_0\\ &\{s_0\}\xrightarrow{ε} \{s_0, s_1, s_2, s_3\}: q_0\\ &\{s_1\}\xrightarrow{b}\{s_2\}\xrightarrow{ε}\{s_0, s_1, s_2, s_3\}: q_0\\ &\{s_2\}\xrightarrow{b}\{s_3\}\xrightarrow{ε}\{s_0, s_1, s_2, s_3\}: q_0\\ &\{s_3\}\xrightarrow{a}\{s_0\}\xrightarrow{ε}\{s_0, s_1, s_2, s_3\}: q_0 \end{aligned} ​初始状态：{s0​}:q0​{s0​}a​{s1​}ε​{s0​,s1​,s2​,s3​}:q0​{s0​}ε​{s0​,s1​,s2​,s3​}:q0​{s1​}b​{s2​}ε​{s0​,s1​,s2​,s3​}:q0​{s2​}b​{s3​}ε​{s0​,s1​,s2​,s3​}:q0​{s3​}a​{s0​}ε​{s0​,s1​,s2​,s3​}:q0​​
得到的DFA为：

题目2

将下列正则表达式转换成 DFA。
（1）（a|b）*
根据Thompson算法将正则表达式逐步转换成NFA：
e -> a|b：

e -> (a|b)*：

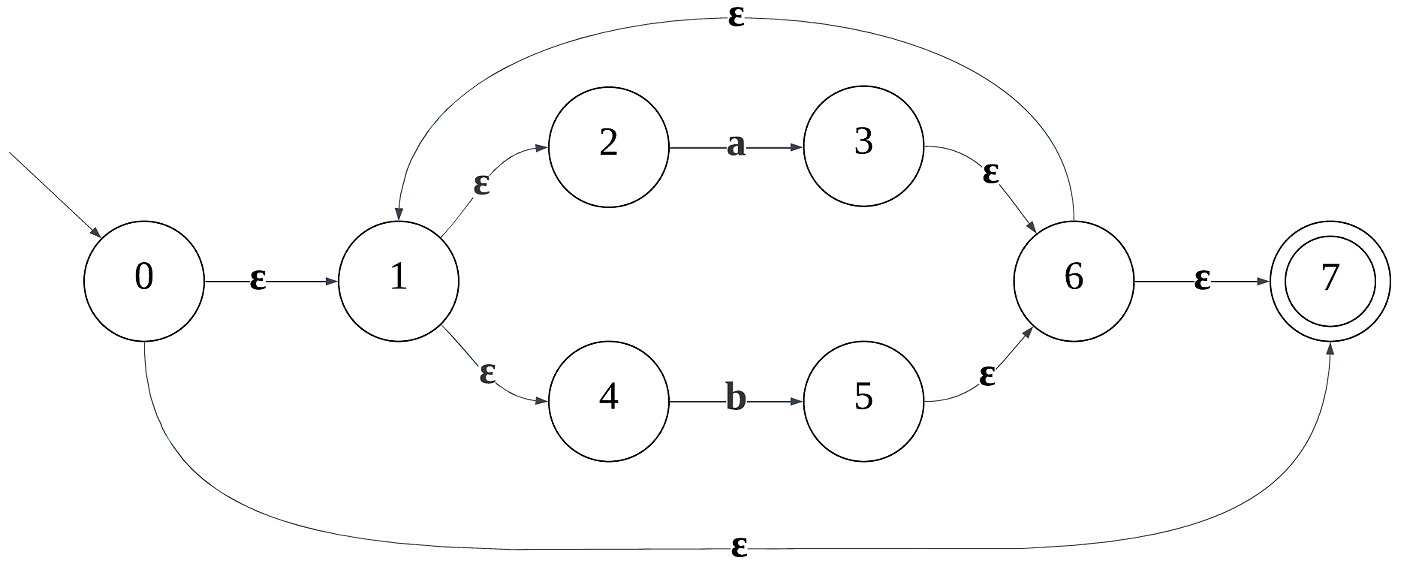
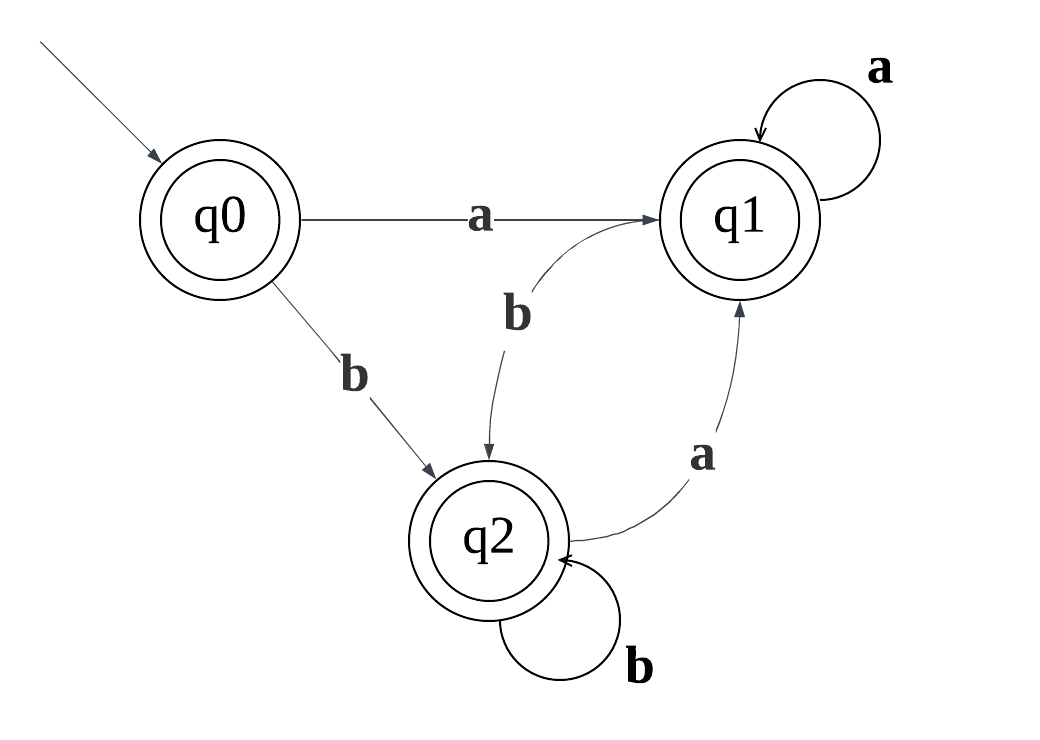
利用子集构造算法将NFA转为DFA：
初始状态：{s0}:q0{q0}→ε{s0,s1,s2,s4,s7}:q0{q0}→a{s3}→ε{s1,s2,s3,s4,s6,s7}:q1{q0}→b{s5}→ε{s1,s2,s4,s5,s6,s7}:q2{q1}→a{s3}→ε{s1,s2,s3,s4,s6,s7}:q1{q1}→b{s5}→ε{s1,s2,s4,s5,s6,s7}:q2{q2}→a{s3}→ε{s1,s2,s3,s4,s6,s7}:q1{q2}→b{s5}→ε{s1,s2,s4,s5,s6,s7}:q2 \begin{aligned} &初始状态：\{s_0\}:q_0\\ &\{q_0\}\xrightarrow{ε}\{s_0, s_1, s_2, s_4, s_7\}:q_0\\ &\{q_0\}\xrightarrow{a}\{s_3\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7\}:q_1\\ &\{q_0\}\xrightarrow{b}\{s_5\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7\}:q_2\\ &\{q_1\}\xrightarrow{a}\{s_3\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7\}:q_1\\ &\{q_1\}\xrightarrow{b}\{s_5\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7\}:q_2\\ &\{q_2\}\xrightarrow{a}\{s_3\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7\}:q_1\\ &\{q_2\}\xrightarrow{b}\{s_5\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7\}:q_2\\ \end{aligned} ​初始状态：{s0​}:q0​{q0​}ε​{s0​,s1​,s2​,s4​,s7​}:q0​{q0​}a​{s3​}ε​{s1​,s2​,s3​,s4​,s6​,s7​}:q1​{q0​}b​{s5​}ε​{s1​,s2​,s4​,s5​,s6​,s7​}:q2​{q1​}a​{s3​}ε​{s1​,s2​,s3​,s4​,s6​,s7​}:q1​{q1​}b​{s5​}ε​{s1​,s2​,s4​,s5​,s6​,s7​}:q2​{q2​}a​{s3​}ε​{s1​,s2​,s3​,s4​,s6​,s7​}:q1​{q2​}b​{s5​}ε​{s1​,s2​,s4​,s5​,s6​,s7​}:q2​​

（2）（a*|b*）*
根据Thompson算法将正则表达式逐步转换成NFA：
e -> a*

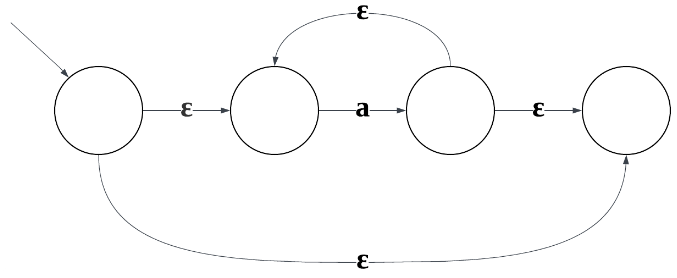
e -> b*

e -> a*|b*

e -> (a*|b*)*

利用子集构造算法将NFA转为DFA：
初始状态：{s0}:q0{q0}→ε{s0,s1,s2,s3,s6,s7,s11}:q0{q0}→a{s4}→ε{s1,s2,s3,s4,s5,s6,s7,s10,s11}:q1{q0}→b{s8}→ε{s1,s2,s3,s6,s7,s8,s9,s10,s11}:q2{q1}→a{s4}→ε{s1,s2,s3,s4,s5,s6,s7,s10,s11}:q1{q1}→b{s8}→ε{s1,s2,s3,s6,s7,s8,s9,s10,s11}:q2{q2}→a{s4}→ε{s1,s2,s3,s4,s5,s6,s7,s10,s11}:q1{q2}→b{s8}→ε{s1,s2,s3,s6,s7,s8,s9,s10,s11}:q2 \begin{aligned} &初始状态：\{s_0\}:q_0\\ &\{q_0\}\xrightarrow{ε}\{s_0, s_1, s_2, s_3, s_6, s_7, s_{11}\}:q_0\\ &\{q_0\}\xrightarrow{a}\{s_4\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_5, s_6, s_7, s_{10}, s_{11}\}:q_1\\ &\{q_0\}\xrightarrow{b}\{s_8\}\xrightarrow{ε}\{s_1, s_2, s_3, s_6, s_7, s_8, s_9, s_{10}, s_{11}\}:q_2\\ &\{q_1\}\xrightarrow{a}\{s_4\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_5, s_6, s_7, s_{10}, s_{11}\}:q_1\\ &\{q_1\}\xrightarrow{b}\{s_8\}\xrightarrow{ε}\{s_1, s_2, s_3, s_6, s_7, s_8, s_9, s_{10}, s_{11}\}:q_2\\ &\{q_2\}\xrightarrow{a}\{s_4\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_5, s_6, s_7, s_{10}, s_{11}\}:q_1\\ &\{q_2\}\xrightarrow{b}\{s_8\}\xrightarrow{ε}\{s_1, s_2, s_3, s_6, s_7, s_8, s_9, s_{10}, s_{11}\}:q_2\\ \end{aligned} ​初始状态：{s0​}:q0​{q0​}ε​{s0​,s1​,s2​,s3​,s6​,s7​,s11​}:q0​{q0​}a​{s4​}ε​{s1​,s2​,s3​,s4​,s5​,s6​,s7​,s10​,s11​}:q1​{q0​}b​{s8​}ε​{s1​,s2​,s3​,s6​,s7​,s8​,s9​,s10​,s11​}:q2​{q1​}a​{s4​}ε​{s1​,s2​,s3​,s4​,s5​,s6​,s7​,s10​,s11​}:q1​{q1​}b​{s8​}ε​{s1​,s2​,s3​,s6​,s7​,s8​,s9​,s10​,s11​}:q2​{q2​}a​{s4​}ε​{s1​,s2​,s3​,s4​,s5​,s6​,s7​,s10​,s11​}:q1​{q2​}b​{s8​}ε​{s1​,s2​,s3​,s6​,s7​,s8​,s9​,s10​,s11​}:q2​​

（3）（a|b）* abb（a|b）*
e -> (a|b)*：

e -> (a|b)*abb(a|b)*：

利用子集构造算法将NFA转为DFA：
初始状态：{s0}:q0{q0}→ε{s0,s1,s2,s4,s7,s8}:q0{q0}→a{s3,s9}→ε{s1,s2,s3,s4,s6,s7,s8,s9}:q1{q0}→b{s5}→ε{s1,s2,s4,s5,s6,s7,s8}:q2{q1}→a{s3,s9}→ε{s1,s2,s3,s4,s6,s7,s8,s9}:q1{q1}→b{s5,s10}→ε{s1,s2,s4,s5,s6,s7,s8,s10}:q3{q2}→a{s3,s9}→ε{s1,s2,s3,s4,s6,s7,s8,s9}:q1{q2}→b{s5}→ε{s1,s2,s4,s5,s6,s7,s8}:q2{q3}→a{s3,s9}→ε{s1,s2,s3,s4,s6,s7,s8,s9}:q1{q3}→b{s5,s11}→ε{s1,s2,s4,s5,s6,s7,s8,s11,s12,s13,s14,s16,s19}:q4{q4}→a{s3,s9,s15}→ε{s1,s2,s3,s4,s6,s7,s8,s9,s13,s14,s15,s16,s18,s19}:q5{q4}→b{s5,s17}→ε{s1,s2,s4,s5,s6,s7,s8,s13,s14,s16,s17,s18,s19}:q6{q5}→a{s3,s9,s15}→ε{s1,s2,s3,s4,s6,s7,s8,s9,s13,s14,s15,s16,s18,s19}:q5{q5}→b{s5,s10,s17}→ε{s1,s2,s4,s5,s6,s7,s8,s10,s13,s14,s16,s17,s18,s19}:q7{q6}→a{s3,s9,s15}→ε{s1,s2,s3,s4,s6,s7,s8,s9,s13,s14,s15,s16,s18,s19}:q5{q6}→b{s5,s17}→ε{s1,s2,s4,s5,s6,s7,s8,s13,s14,s16,s17,s18,s19}:q6{q7}→a{s3,s9,s15}→ε{s1,s2,s3,s4,s6,s7,s8,s9,s13,s14,s15,s16,s18,s19}:q5{q7}→b{s5,s11,s17}→ε{s1,s2,s4,s5,s6,s7,s8,s11,s12,s13,s14,s16,s17,s18,s19}:q8{q8}→a{s3,s9,s15}→ε{s1,s2,s3,s4,s6,s7,s8,s9,s13,s14,s15,s16,s18,s19}:q5{q8}→b{s5,s17}→ε{s1,s2,s4,s5,s6,s7,s8,s13,s14,s16,s17,s18,s19}:q6 \begin{aligned} &初始状态：\{s_0\}:q_0\\ &\{q_0\}\xrightarrow{ε}\{s_0, s_1, s_2, s_4, s_7, s_8\}:q_0\\ &\{q_0\}\xrightarrow{a}\{s_3, s_9\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9\}:q_1\\ &\{q_0\}\xrightarrow{b}\{s_5\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8\}:q_2\\ &\{q_1\}\xrightarrow{a}\{s_3, s_9\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9\}:q_1\\ &\{q_1\}\xrightarrow{b}\{s_5, s_{10}\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8, s_{10}\}:q_3\\ &\{q_2\}\xrightarrow{a}\{s_3, s_9\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9\}:q_1\\ &\{q_2\}\xrightarrow{b}\{s_5\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8\}:q_2\\ &\{q_3\}\xrightarrow{a}\{s_3, s_9\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9\}:q_1\\ &\{q_3\}\xrightarrow{b}\{s_5, s_{11}\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8, s_{11}, s_{12}, s_{13}, s_{14}, s_{16}, s_{19}\}:q_4\\ &\{q_4\}\xrightarrow{a}\{s_3, s_9, s_{15}\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9, s_{13}, s_{14}, s_{15}, s_{16}, s_{18}, s_{19}\}:q_5\\ &\{q_4\}\xrightarrow{b}\{s_5, s_{17}\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8, s_{13}, s_{14}, s_{16}, s_{17}, s_{18}, s_{19}\}:q_6\\ &\{q_5\}\xrightarrow{a}\{s_3, s_9, s_{15}\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9, s_{13}, s_{14}, s_{15}, s_{16}, s_{18}, s_{19}\}:q_5\\ &\{q_5\}\xrightarrow{b}\{s_5, s_{10}, s_{17}\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8, s_{10}, s_{13}, s_{14}, s_{16}, s_{17}, s_{18}, s_{19}\}:q_7\\ &\{q_6\}\xrightarrow{a}\{s_3, s_9, s_{15}\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9, s_{13}, s_{14}, s_{15}, s_{16}, s_{18}, s_{19}\}:q_5\\ &\{q_6\}\xrightarrow{b}\{s_5, s_{17}\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8, s_{13}, s_{14}, s_{16}, s_{17}, s_{18}, s_{19}\}:q_6\\ &\{q_7\}\xrightarrow{a}\{s_3, s_9, s_{15}\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9, s_{13}, s_{14}, s_{15}, s_{16}, s_{18}, s_{19}\}:q_5\\ &\{q_7\}\xrightarrow{b}\{s_5, s_{11}, s_{17}\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8, s_{11}, s_{12}, s_{13}, s_{14}, s_{16}, s_{17}, s_{18}, s_{19}\}:q_8\\ &\{q_8\}\xrightarrow{a}\{s_3, s_9, s_{15}\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9, s_{13}, s_{14}, s_{15}, s_{16}, s_{18}, s_{19}\}:q_5\\ &\{q_8\}\xrightarrow{b}\{s_5, s_{17}\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8, s_{13}, s_{14}, s_{16}, s_{17}, s_{18}, s_{19}\}:q_6 \end{aligned} ​初始状态：{s0​}:q0​{q0​}ε​{s0​,s1​,s2​,s4​,s7​,s8​}:q0​{q0​}a​{s3​,s9​}ε​{s1​,s2​,s3​,s4​,s6​,s7​,s8​,s9​}:q1​{q0​}b​{s5​}ε​{s1​,s2​,s4​,s5​,s6​,s7​,s8​}:q2​{q1​}a​{s3​,s9​}ε​{s1​,s2​,s3​,s4​,s6​,s7​,s8​,s9​}:q1​{q1​}b​{s5​,s10​}ε​{s1​,s2​,s4​,s5​,s6​,s7​,s8​,s10​}:q3​{q2​}a​{s3​,s9​}ε​{s1​,s2​,s3​,s4​,s6​,s7​,s8​,s9​}:q1​{q2​}b​{s5​}ε​{s1​,s2​,s4​,s5​,s6​,s7​,s8​}:q2​{q3​}a​{s3​,s9​}ε​{s1​,s2​,s3​,s4​,s6​,s7​,s8​,s9​}:q1​{q3​}b​{s5​,s11​}ε​{s1​,s2​,s4​,s5​,s6​,s7​,s8​,s11​,s12​,s13​,s14​,s16​,s19​}:q4​{q4​}a​{s3​,s9​,s15​}ε​{s1​,s2​,s3​,s4​,s6​,s7​,s8​,s9​,s13​,s14​,s15​,s16​,s18​,s19​}:q5​{q4​}b​{s5​,s17​}ε​{s1​,s2​,s4​,s5​,s6​,s7​,s8​,s13​,s14​,s16​,s17​,s18​,s19​}:q6​{q5​}a​{s3​,s9​,s15​}ε​{s1​,s2​,s3​,s4​,s6​,s7​,s8​,s9​,s13​,s14​,s15​,s16​,s18​,s19​}:q5​{q5​}b​{s5​,s10​,s17​}ε​{s1​,s2​,s4​,s5​,s6​,s7​,s8​,s10​,s13​,s14​,s16​,s17​,s18​,s19​}:q7​{q6​}a​{s3​,s9​,s15​}ε​{s1​,s2​,s3​,s4​,s6​,s7​,s8​,s9​,s13​,s14​,s15​,s16​,s18​,s19​}:q5​{q6​}b​{s5​,s17​}ε​{s1​,s2​,s4​,s5​,s6​,s7​,s8​,s13​,s14​,s16​,s17​,s18​,s19​}:q6​{q7​}a​{s3​,s9​,s15​}ε​{s1​,s2​,s3​,s4​,s6​,s7​,s8​,s9​,s13​,s14​,s15​,s16​,s18​,s19​}:q5​{q7​}b​{s5​,s11​,s17​}ε​{s1​,s2​,s4​,s5​,s6​,s7​,s8​,s11​,s12​,s13​,s14​,s16​,s17​,s18​,s19​}:q8​{q8​}a​{s3​,s9​,s15​}ε​{s1​,s2​,s3​,s4​,s6​,s7​,s8​,s9​,s13​,s14​,s15​,s16​,s18​,s19​}:q5​{q8​}b​{s5​,s17​}ε​{s1​,s2​,s4​,s5​,s6​,s7​,s8​,s13​,s14​,s16​,s17​,s18​,s19​}:q6​​