HNU 数据挖掘 实验二 实验报告

实验二 数据降维与可视化

1. 实验目的

1. 熟悉常见的数据预处理方法，掌握信息增益、Pearson、Spearman、Kendall 等相关性分析手段。
2. 掌握常见无监督数据降维方法（PCA、ICA、UMAP、t-SNE、LLE 等）。
3. 掌握将数据降至 2D/3D 并进行可视化展示的方法。
4. 能够比较不同降维方法的优缺点。
5. （选做）利用降维结果辅助完成聚类或分类，以评估降维质量。

2. 实验环境

• 操作系统：Windows
• 开发环境：DM（Data Mining）Anaconda环境
• 可能用到的语言/库（若适用）：Python、sklearn、umap-learn、matplotlib、seaborn等
• 数据集：CuMiDa 的脑癌基因表达数据集 GSE50161
  该数据库包含 78 个癌症微阵列数据集，这些数据集均来自基因表达综合数据库 (GEO) 的 30,000 项研究。CuMiDa 的目标是提供这些数据集的统一且先进的生物学预处理，并可用于 PCA 和 t-SNE 分析。CuMiDa数据集经过人工精心筛选，包括样本质量控制、去除无关探针、背景校正和标准化等，从而为计算研究创建更可靠的数据来源。

3. 实验原理与方法

3.1 数据预处理与相关性分析

本节介绍了信息增益、Pearson、Spearman、Kendall τ四种常见的数据分析方法，它们从不同角度衡量特征与目标变量（或两个变量之间）的关系。下面对四种方法进行总结：

3.1.1 信息增益（Information Gain）

定义
信息增益衡量特征 $X$ 对目标变量 $Y$ 的不确定性减少量。其数学定义为：
$$IG(Y;X)=H(Y)-H(Y\mid X)$$
其中

• $H(Y)$：标签 $Y$ 的熵
  $$H(Y)=-\sum _{y}P(Y=y){\log }_{2}P(Y=y)$$
• 条件熵
  $$H(Y\mid X)=\sum _{x}P(X=x)H(Y\mid X=x)$$
  直观理解
  信息增益越大，说明特征 $X$ 能提供越多关于标签 $Y$ 的信息。
  特点
• 能捕捉任意非线性关系
• 常用于决策树（ID3、C4.5）与特征选择
• 对连续特征需要离散化或互信息估计

3.1.2 Pearson 相关系数

定义
Pearson 相关系数衡量连续变量之间的线性关系：
$$r_{XY}=\frac{\mathrm{cov}(X,Y)}{{\sigma }_X{\sigma }_Y}$$
协方差定义为：
$$\mathrm{cov}(X,Y)=\frac{1}{n}\sum _{i=1}^n(x_i-\bar{x})(y_i-\bar{y})$$
最终得到 $$r\in [-1,1]$$解释

• $r=1$：完全正线性
• $r=-1$：完全负线性
• $r=0$：无线性关系
  特点
• 用于检测线性趋势
• 对异常值非常敏感
• 不适合用于分类或等级数据

3.1.3 Spearman S 相关系数

定义
Spearman 相关系数基于秩（rank），用于衡量变量是否存在单调关系。
先将数据转秩后再计算 Pearson 相关。
当无秩并列（ties）时可用简化公式：
$$\rho =1-\frac{6{\sum }_{i=1}^n{d}_i^2}{n(n^2-1)}$$
其中

• $d_i$：两个变量的秩差
• $n$：样本数量
  特点
• 可以检测非线性但单调的关系
• 对异常值不敏感（因为基于 rank）
• 常用于排名、等级数据

3.1.4 Kendall τ 相关系数

定义
Kendall τ 通过比较所有样本对之间是否“秩一致”来衡量相关性。
$$\tau =\frac{C-D}{\left(\genfrac{}{}{0ex}{}{n}{2}\right)}$$
其中

• $C$：一致对（concordant pairs）个数
• $D$：不一致对（discordant pairs）个数
• $\left(\genfrac{}{}{0ex}{}{n}{2}\right)$：所有样本对的数量
  解释
  τ 的值表示：

“任意抽取一对样本，它们的排序一致的概率与不一致的概率之差”。
$$\tau \in [-1,1]$$

特点

• 对秩数据、离群点更稳定
• 计算复杂度高（适用于中小数据集）
• 比 Spearman 有更强的统计解释性

3.1.5 对比总结

指标	捕捉关系	数据类型	异常值敏感度	典型应用
信息增益	任意依赖	离散/离散化连续	中等	特征选择、决策树
Pearson	线性	连续型	高	数值型线性关系检测
Spearman	单调（含非线性）	连续/等级	低	排名、单调关系
Kendall τ	单调（概率解释）	连续/等级	很低	小样本、秩稳定分析

3.2 无监督降维算法原理

下面对 5 种常见无监督降维方法做详解：PCA、ICA、UMAP、t-SNE、LLE。每个小节包含：算法思想、关键数学公式 / 步骤、优点与局限。

3.2.1 PCA（Principal Component Analysis）

算法思想
PCA 试图在低维线性子空间中尽可能保留原始数据的方差。等价地，寻找一组正交基，使得数据在前 $k$ 个基上的投影方差最大，从而达到降维。
数学表述（核心）
给定中心化后的数据矩阵 $X\in {\mathbb{R}}^{n\times d}$（每行样本，每列特征，已减去均值），协方差矩阵为
$$C=\frac{1}{n}{X}^{\top }X.$$
PCA 求解 $C$ 的特征值分解（或 SVD）：
$$C{v}_i={\lambda }_i{v}_i,{\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_d\ge 0.$$
取前 $k$ 个特征向量 $V_k=[v_1,\dots ,v_k]$，低维表示为：
$$Z=X{V}_k(Z\in {\mathbb{R}}^{n\times k}).$$
几何/优化解释
PCA 也可以看成求解：
$$\underset{V\in {\mathbb{R}}^{d\times k},V^{\top }V=I}{\max }\mathrm{tr}(V^{\top }CV),$$
即最大化投影后的总方差。
优点

• 计算稳定（可用 SVD），解释性强（各主成分方差解释比例）。
• 线性变换，投影简单（矩阵乘法）。
• 常作为预处理（去噪、压缩、可视化的基线方法）。
  局限
• 只保留线性结构，无法捕捉非线性流形。
• 对尺度敏感：需先标准化/归一化（尤其不同量纲时）。
• 对异常值敏感（异常点会扭曲主方向）。

3.2.2 ICA（Independent Component Analysis）

算法思想
ICA 假设观测是若干统计独立源信号的线性混合，目标是从观测中恢复出这些独立成分（盲信号分离）。不同于 PCA 的正交无关（uncorrelated），ICA 追求的是统计独立（independent）。
线性混合模型
观测向量 $x\in {\mathbb{R}}^d$ 表示为：
$$x=As,$$
其中 $s\in {\mathbb{R}}^d$ 是源信号（独立分量），$A$ 是未知混合矩阵。目标是找到反混合矩阵 $W$ 使得
$$\hat{s}=Wx$$
使得 $\hat{s}$ 的分量尽可能相互独立。
独立性的度量 / 优化目标
常通过最大化非高斯性（non-Gaussianity）来实现（依据中心极限定理：独立成分通常比混合更非高斯）。常用的非高斯性度量包括：

• 峭度（kurtosis）：第四阶中心矩
• 近熵（negentropy）：基于熵的度量
  或通过最小化互信息（mutual information）实现独立性。
  举例：最大化峭度或近熵得到优化问题，常用快速 ICA（FastICA）算法通过迭代固定点法求解。
  优点
• 能分离混合信号（如盲源分离、音频分离、神经信号处理）。
• 比 PCA 更强的表示能力（独立性强于无相关）。
  局限
• 模型假设较强：假设源信号互相独立且至少有一个非高斯分量。
• 仅能分离线性混合（非线性混合需更复杂方法）。
• 排序与符号不确定：结果分量的顺序与符号不可识别（需要后处理解释）。

3.2.3 UMAP（Uniform Manifold Approximation and Projection）

核心思想
UMAP 基于流形学习与代数拓扑思想，假设数据来自某个低维流形。其目标是构建高维数据的局部邻域拓扑表示（模糊单纯形集，fuzzy simplicial set），再在低维空间中找到一个拓扑近似，使得高维和低维的模糊集合相似（优化交叉熵）。
主要步骤（简要）

1. 构建近邻图：对每个点计算 $k$ 个最近邻（通常用欧氏距离或其他度量），并用局部平滑参数（每点的局部尺度）使邻接权重自适应。
2. 构造模糊单纯形集：将近邻关系转化为概率/权重（模糊集），得到高维数据的拓扑描述。
3. 低维嵌入优化：在低维空间随机初始化点位，最小化高维与低维模糊单纯形集之间的交叉熵（类似最小化某种损失），通常使用随机梯度下降优化。
   数学/直观要点

• UMAP 的距离-到-连接权重函数和局部尺度的处理使其在局部结构和全局连贯性之间取得平衡。
• 在数学基础上，UMAP 依赖流形假设和 Riemannian 度量的一些近似，并借助拓扑等价性来约束低维表示。
  算法特点
• 保留局部结构，较好反映数据簇的连续形态与全局大致布局（比 t-SNE 更保留一些全局结构）。
• 计算速度相对较快，适合大规模数据（有优化的近邻搜索与稀疏图表示）。
• 支持多种距离度量，参数较多但直观（例如 n_neighbors 控制局部规模，min_dist 控制嵌入中点的最小距离/紧密度）。
  优点
• 速度快、可扩展到较大数据集。
• 能兼顾局部与一定程度的全局结构。
• 结果通常保留簇形与连通性，易于用于可视化与下游任务（如聚类初始化）。
  局限
• 参数敏感（n_neighbors, min_dist 等会显著影响结果），需实验调参。
• 理论上基于流形假设，不适用于不满足该假设的数据。
• 嵌入仍具有随机性（初始化与随机过程可影响），需要多次实验以确认稳定性。

3.2.4 t-SNE（t-distributed Stochastic Neighbor Embedding）

算法思想（直观）
t-SNE 将高维点对间相似度转成概率分布，在低维空间中也定义一个概率分布（但用 heavier-tailed 的 Student-t 分布），并通过最小化两个分布之间的 Kullback–Leibler（KL）散度来得到嵌入。目的是尽可能保留高维数据的局部邻域结构（同近邻概率保持一致）。
数学要点

• 高维相似度（对 i, j 点）定义为条件概率（基于 Gaussian）：
  $$p_{j|i}=\frac{\exp (-\Vert x_i-x_j{\Vert }^2/2{\sigma }_i^2)}{{\sum }_{k\ne i}\exp (-\Vert x_i-x_k{\Vert }^2/2{\sigma }_i^2)}$$
  再对称化得到
  $$p_{ij}=\frac{p_{j|i}+p_{i|j}}{2n}.$$
• 低维相似度使用 Student-$t$（自由度 1，重尾）：
  $$q_{ij}=\frac{(1+\Vert y_i-y_j{\Vert }^2{)}^{-1}}{{\sum }_{k\ne l}(1+\Vert y_k-y_l{\Vert }^2{)}^{-1}}.$$
• 优化目标：最小化 KL 散度
  $$\mathrm{KL}(P\Vert Q)=\sum _{i\ne j}{p}_{ij}\log \frac{p_{ij}}{q_{ij}}.$$
  局部结构保留特性
  t-SNE 强调保留高维数据中“近邻”的相对关系，即把高相似度点对在低维靠得很近；对不相似点对的相距大小相对不做精确要求。使用 t 分布能避免“拥挤问题”，使不同簇之间保持较远距离。
  关键参数与影响
• perplexity：控制每个点在高维上期望的有效近邻数（类似平滑尺度）。小 perplexity 强调极小局部结构（簇更细），大 perplexity 强调更宽的局部邻域（可能融合簇）。常用范围 5–50。
• learning rate（学习率）：过小收敛慢；过大可能导致嵌入不稳定或出现碎裂结构。
• 迭代次数、初始化（PCA 初始化 vs 随机）也会影响结果。
  优点
• 在可视化上非常擅长将簇分离开，展示高维数据的局部结构。
• 对复杂非线性结构有很好的“看图”效果。
  局限
• 计算成本高（尤其是在大数据上），现代实现使用 Barnes-Hut 或 FFT-based 加速以提升规模。
• 不保留全局结构（不同运行之间全局布局可能不同），不适合直接用于下游需要保持全局度量的任务。
• 参数敏感，需要多次调参（尤其 perplexity）。
• 结果可解释性低，不适合作为特征压缩保存再训练模型（除非谨慎验证）。

3.2.5 LLE（Locally Linear Embedding）

核心思想
LLE 假设数据在高维空间上局部接近线性（局部线性可表示为其邻居的加权线性组合）。LLE 的目标是在低维空间中保持这些局部线性重构权重，从而保留流形的局部几何结构。
算法步骤（概要）

1. 寻找最近邻：对每个数据点 $x_i$ 找到它的 $K$ 个最近邻。
2. 求解重构权重：对每个点，求最小化重构误差来计算权重 $w_{ij}$：
   $$\underset{w_{ij}}{\min }\sum _i\Vert x_i-\sum _{j\in \mathcal{N}(i)}{w}_{ij}{x}_j{\Vert }^2$$
   约束条件：对于每个 $i$，${\sum }_j{w}_{ij}=1$（保持平移不变性）。
3. 低维嵌入保持权重：求低维坐标 $y_i$ 使得同样的权重重构误差最小：
   $$\underset{Y}{\min }\sum _i\Vert y_i-\sum _{j\in \mathcal{N}(i)}{w}_{ij}{y}_j{\Vert }^2$$
   这可转化为求解关于矩阵 $(I-W{)}^{\top }(I-W)$ 的最小特征向量问题（取第 2 到第 $d^{\prime }$ 个特征向量作为嵌入，第一特征向量是常数向量对应零特征值）。
   算法特点

• 明确保留局部线性结构（通过权重矩阵）。
• 嵌入由求特征向量实现（线性代数问题），通常规模受样本数制约（需要解 $n\times n$ 矩阵的特征问题）。
  优点
• 能有效恢复某些类型的非线性流形（当流形确实是局部线性近似时）。
• 方法直观（保持局部重构权重），对平移不变。
  局限
• 对噪声、邻域大小 $K$ 敏感（$K$ 太小或太大都会破坏结果）。
• 计算复杂度高（需解 $n\times n$ 的特征问题，内存对大样本不友好）。
• 无法很好处理非均匀采样或存在短路（近邻跨越真实流形远距离点）的问题。
• 只在样本点上定义嵌入，不直接给出新点的映射（需要 out-of-sample 技术）。

3.2.6 小结（选择建议）

• PCA：需要快速、可解释的线性降维或做预处理时使用。
• ICA：假定数据是独立源的线性混合（如盲源分离、信号分离）时使用。
• UMAP：大数据可视化或希望兼顾局部与部分全局结构时优先（速度与可扩展性好）。
• t-SNE：追求高质量二维/三维可视化以观察簇结构时使用（注意参数调优与可重复性）。
• LLE：在数据满足局部线性流形假设且样本规模适中时可尝试，尤其用于理论学习与小样本流形恢复。

4. 实验步骤

4.1 数据加载与预处理

4.1.1 数据集概览

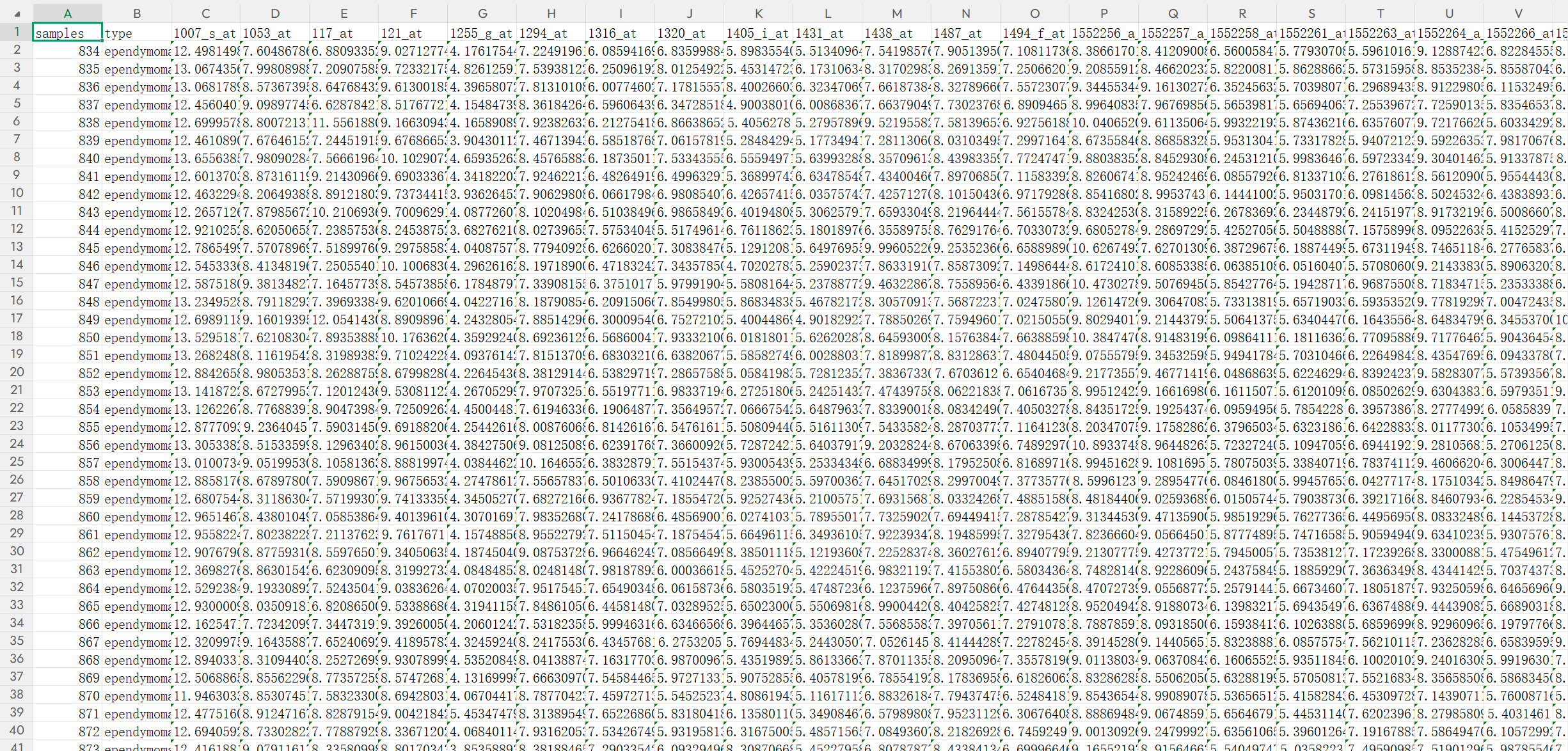
Brain_GSE50161 数据集来自 NCBI GEO（GSE50161），是典型的脑部肿瘤基因表达数据，用 Affymetrix GPL570 平台测序。
基本情况

• 样本数：约 130
• 基因特征数：≈ 54,000 probe
• 数据类型：log2 表达量
  肿瘤类型
  常见标签包括：
• ependymoma（室管膜瘤）
• medulloblastoma（髓母细胞瘤）
• glioblastoma（胶质母细胞瘤）
• astrocytoma（星形细胞瘤）
• normal（正常脑组织）
  数据矩阵说明

1. 每一行对应一个脑组织样本，如：

• samples: 样本编号
• type: 肿瘤类型
• 后面每列是对应基因的表达值
  例如：

samples	type	1007_s_at	1053_at	…
834	ependymoma	12.49	6.60	…

2. 从第三列开始为 Affymetrix probe，如：

• 1007_s_at
• 1053_at
• 117_at
• …
  每个 probe 对应某个基因或基因片段。

3. 数值：log2 表达量
   如：

• 1007_s_at = 12.49
• 1053_at = 6.60
  数值越大 → 对应基因表达越高。
  数据特点
• 高维：每个样本 5 万 + 特征，非常适合降维实验（PCA / t-SNE / UMAP）
• 多类别：包含多种脑瘤类型
• 真实生物数据：噪声较大、异质性强，更能反映降维方法性能

4.1.2 缺失值处理、归一化、标准化等

4.2 特征相关性分析

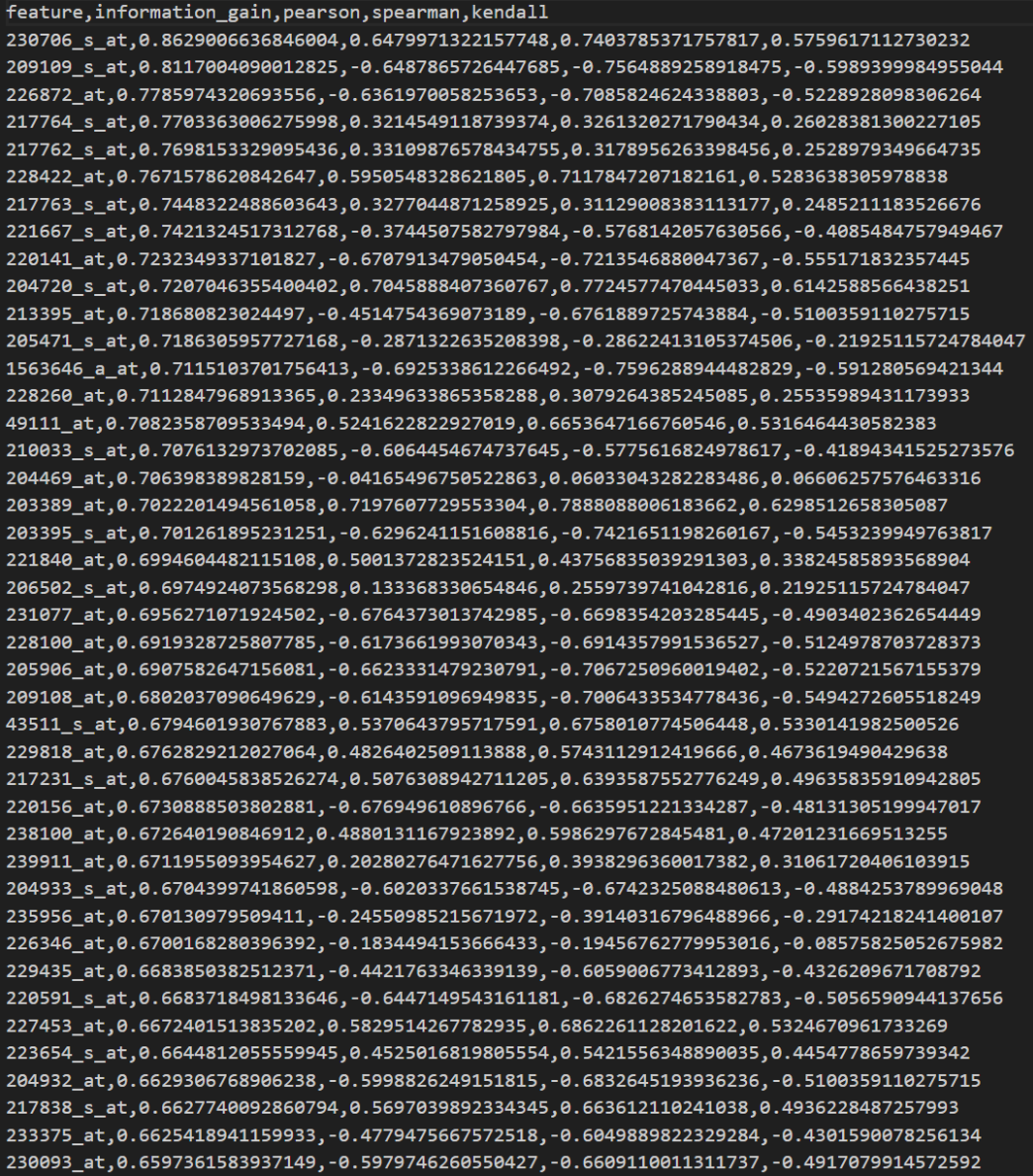
4.2.1 信息增益排序表（部分）

4.2.2 Pearson/Spearman/Kendall 相关矩阵图

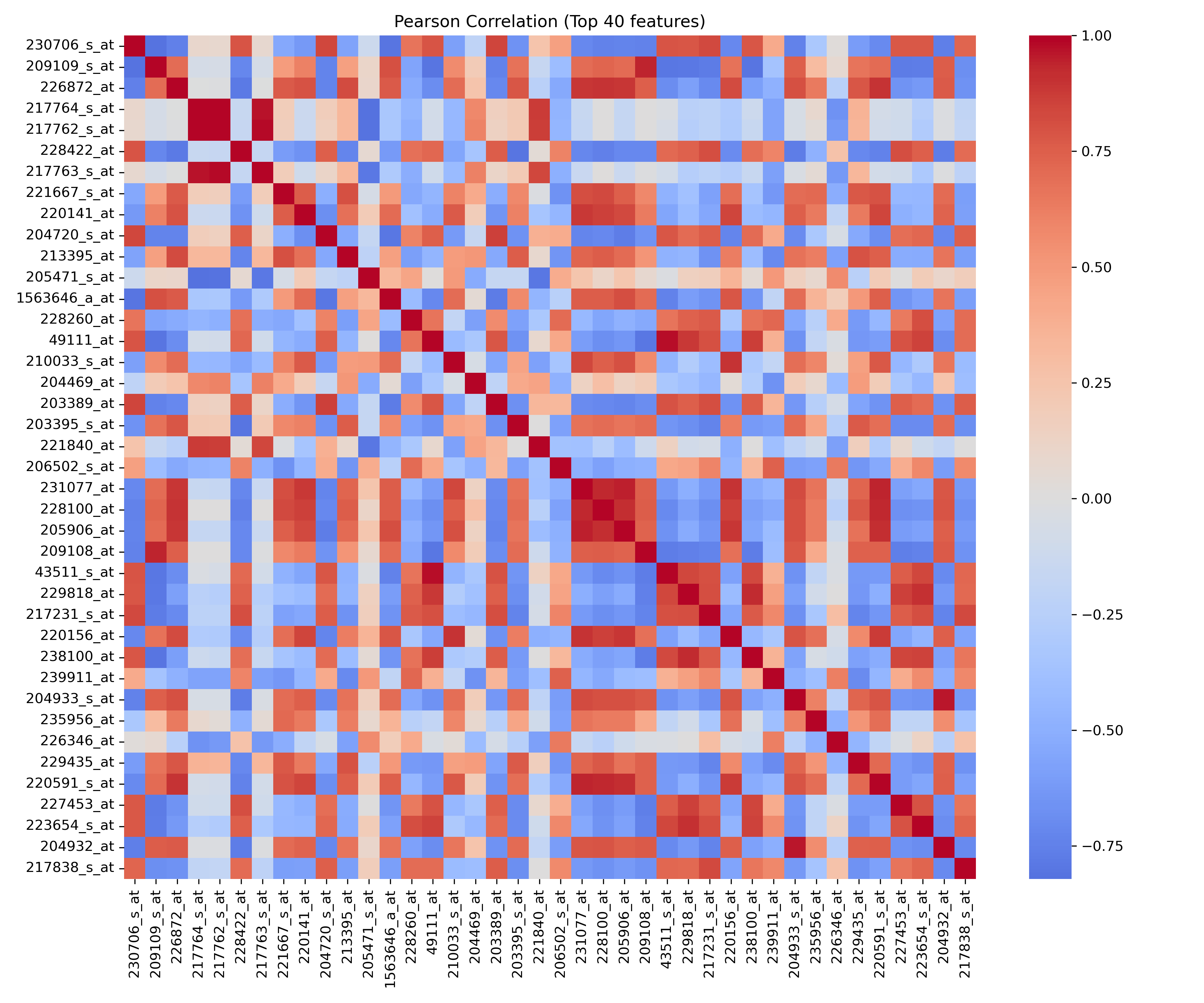
Pearson：

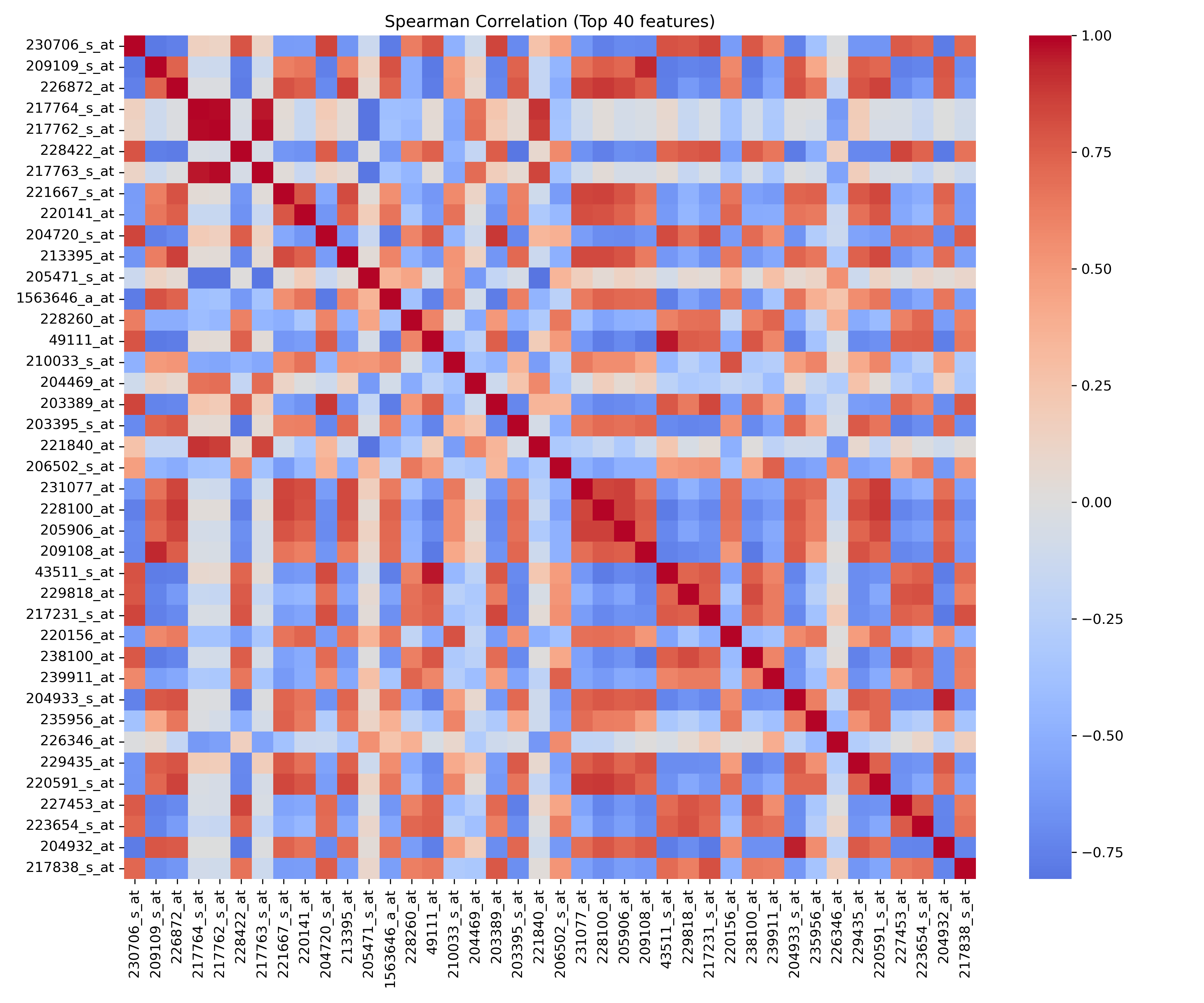
Spearman：

Kendall：

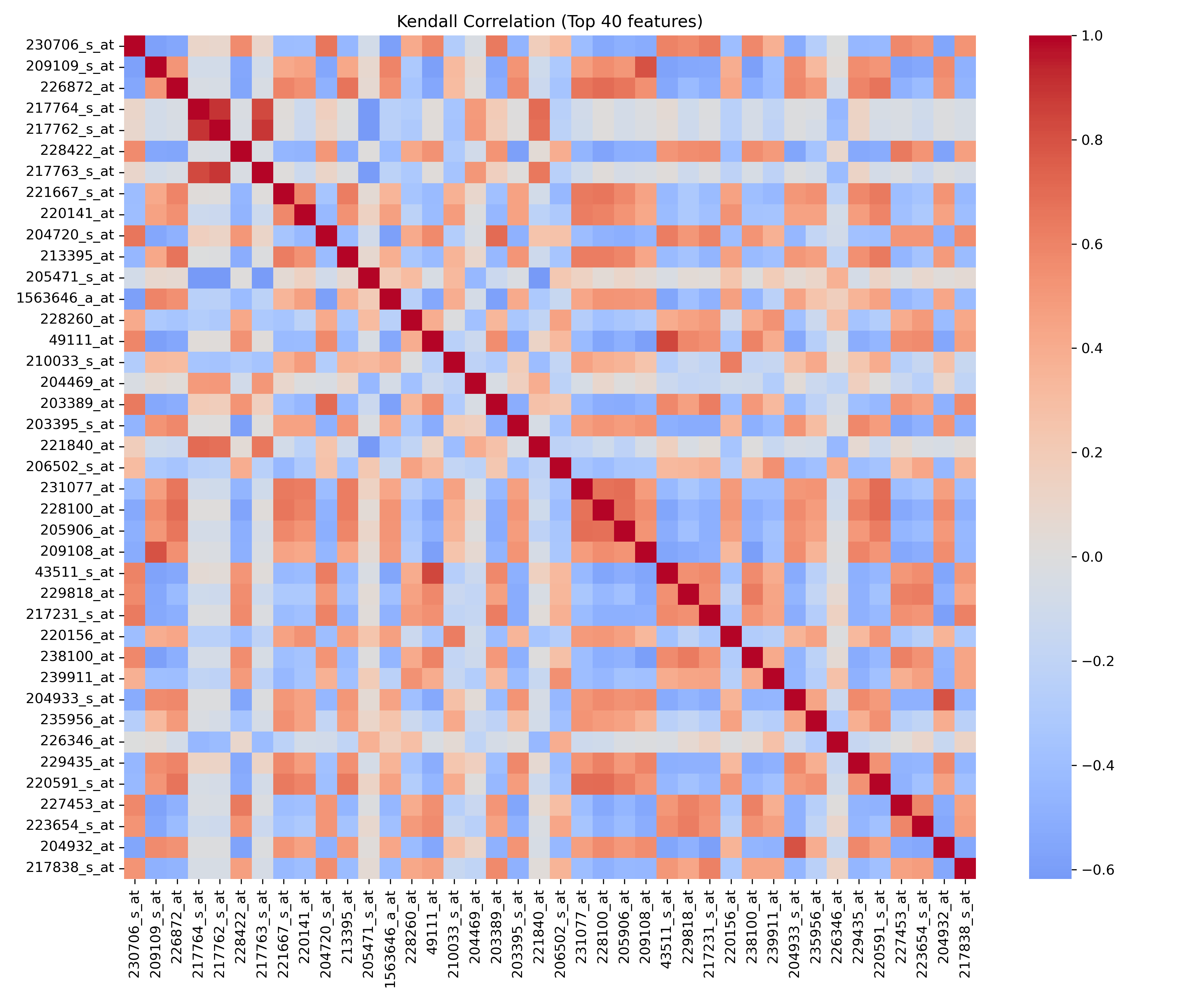
4.2.3 分析结果简述

特征重要性分析
从信息增益排序表来看，特征"230706_s_at"的信息增益最高（0.8629），表明它对目标变量的预测能力最强；其他特征如"209109_s_at"（0.8117）和"226872_at"（0.7786）也表现出较高重要性。信息增益值均大于0.7，说明这些特征整体上能有效减少不确定性，可作为模型中的关键预测因子。
特征相关性分析
Pearson、Spearman和Kendall相关矩阵图均显示相似的模式：主对角线为深红色，表示特征自相关；其他区域颜色混杂，但未出现大面积强相关区块。例如，特征"230706_s_at"与"204720_s_at"在Pearson图中呈正相关（红色），而"209109_s_at"与部分特征呈负相关（蓝色）。三种相关系数在符号和强度上基本一致，表明相关性分析稳健，特征间冗余度较低，但局部存在中等相关或负相关对。
综合分析结果
结合信息增益和相关性，高重要性特征（如Top 10）应优先保留，但需检查相关矩阵以避免共线性（如强相关特征对可去重）。整体特征集质量较好，相关性适中，建议在建模时使用正则化或特征选择方法（如递归消除）来优化性能，确保模型既高效又稳定。

4.3 降维算法实现

全部实验基于 Brain_GSE50161.csv，特征经标准化并限制在方差最高的子集以保证可视化质量。

4.3.1 PCA 降维与可视化

• 使用参数：n_components=2, whiten=False

• 可视化散点图：
  

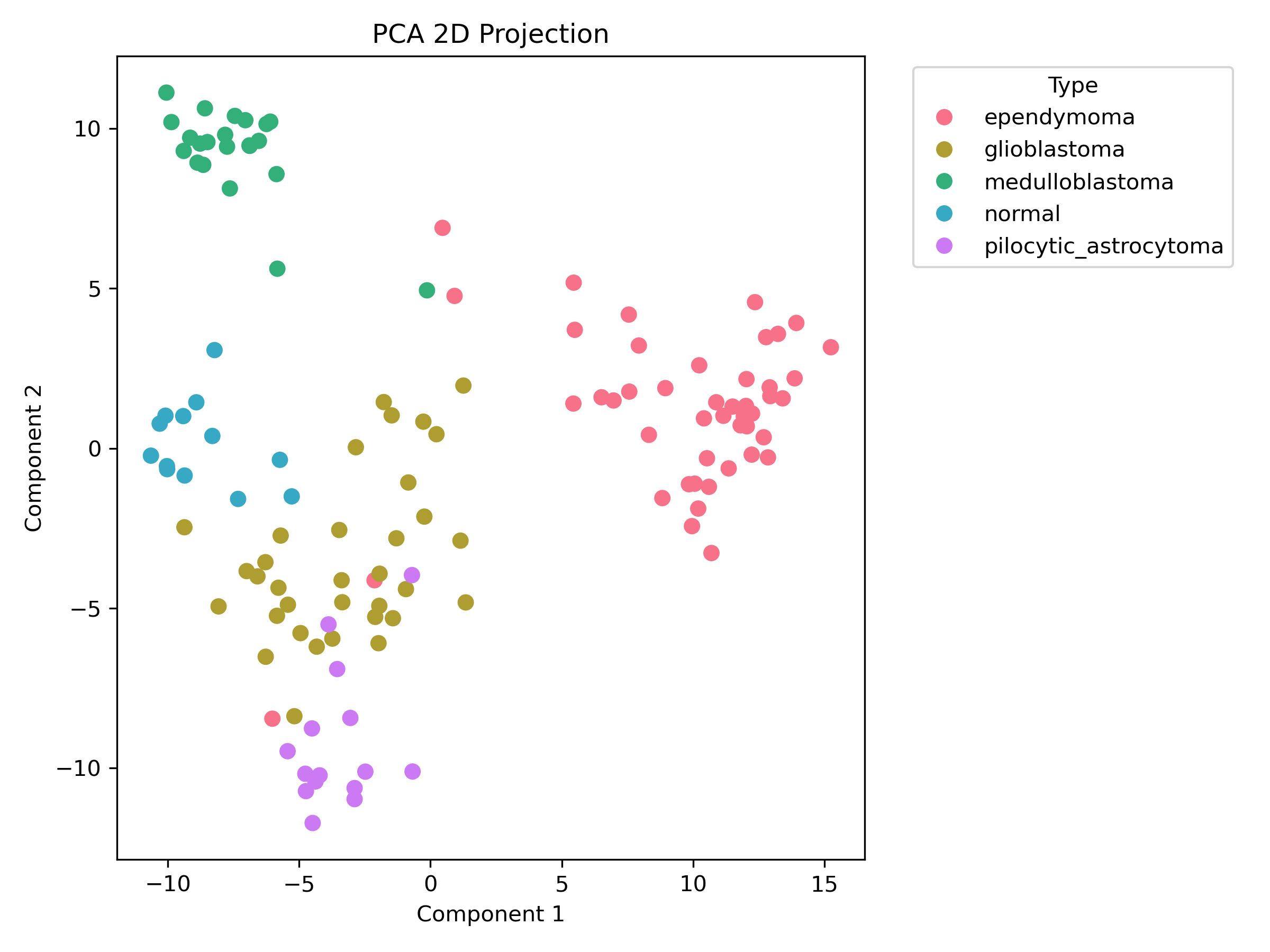
• 时间开销：0.07 秒

• 信任度（trustworthiness）：0.944

• 噪声敏感度：0.0111（特征加入 σ=0.01 高斯噪声）

• explained_variance_ratio：0.48144615869512897

4.3.2 t-SNE 降维与可视化

• 使用参数：n_components=2, perplexity=30, learning_rate=auto, max_iter=1000, init=pca

• 可视化散点图：
  

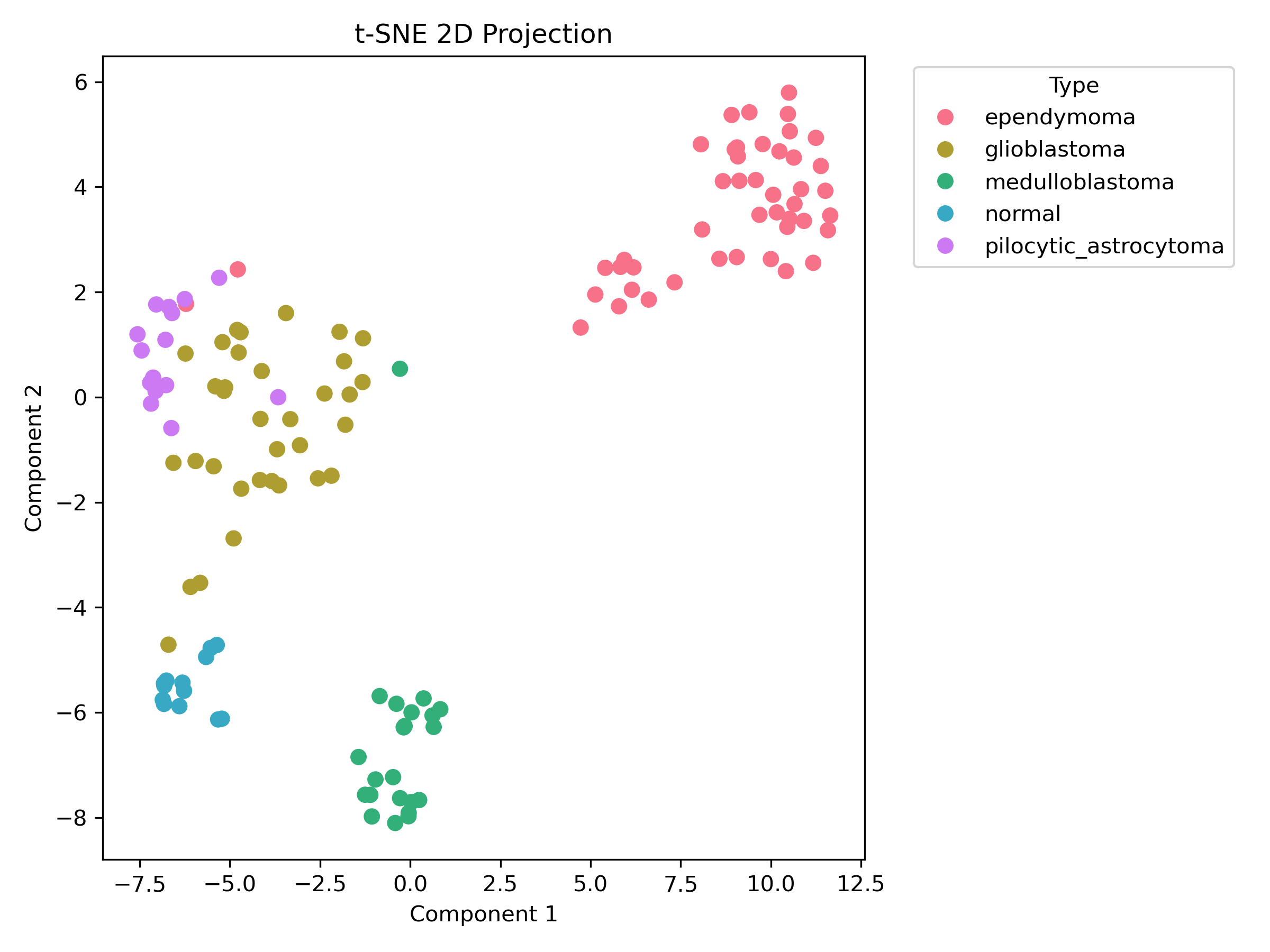
• 时间开销：5.82 秒

• 信任度（trustworthiness）：0.978（相对 PCA 提升 0.035）

• 噪声敏感度：0.6678（特征加入 σ=0.01 高斯噪声）

• kl_divergence：0.1682446449995041

4.3.3 ICA 降维与可视化

• 使用参数：n_components=2, max_iter=800, tol=0.001

• 可视化散点图：
  

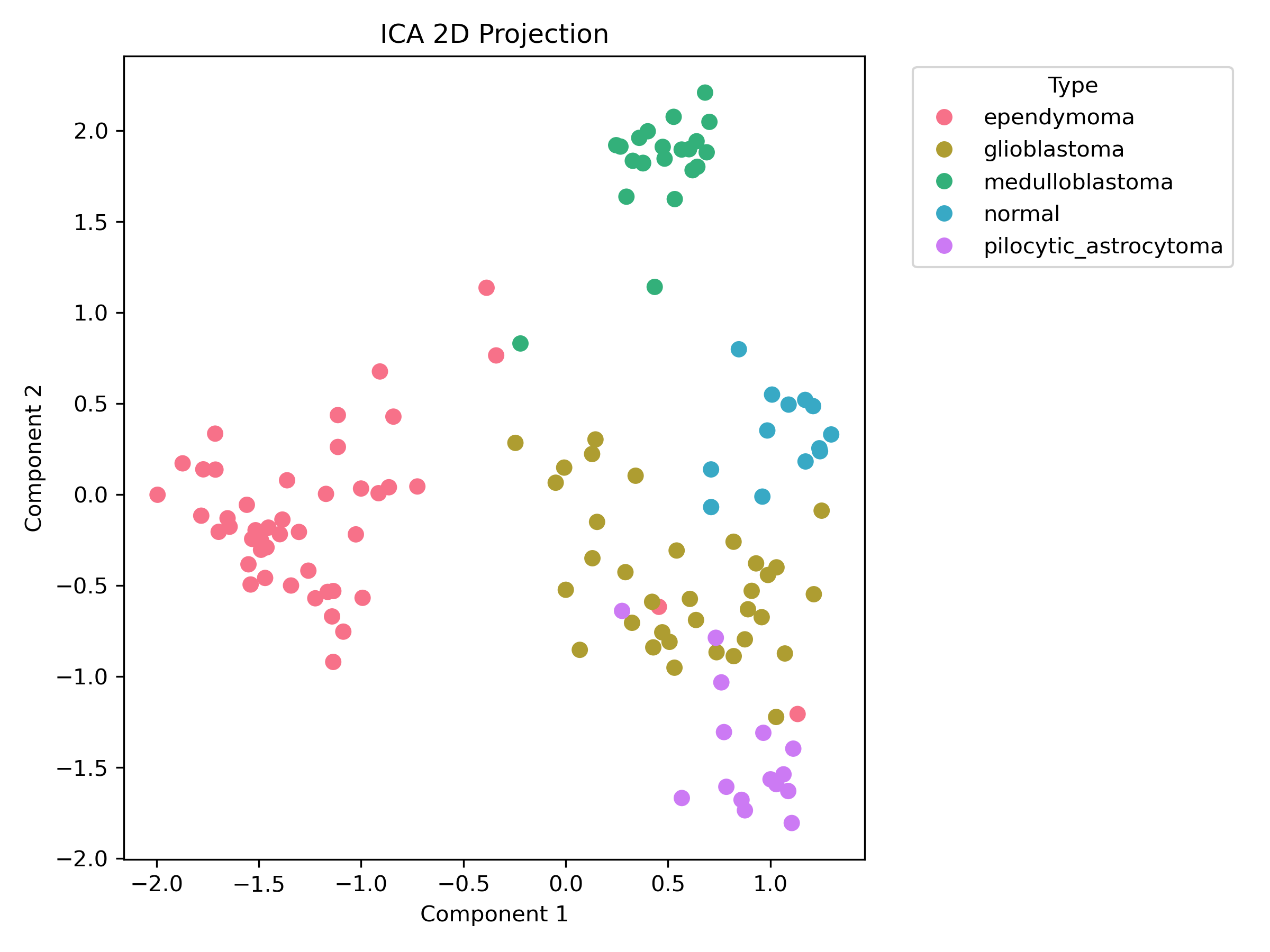
• 时间开销：0.04 秒

• 信任度（trustworthiness）：0.942（相对 PCA 下降 0.001）

• 噪声敏感度：0.0016（特征加入 σ=0.01 高斯噪声）

• avg_abs_kurtosis：0.7176438316982362

4.3.4 UMAP 降维与可视化

• 使用参数：n_components=2, n_neighbors=15, min_dist=0.15, metric=euclidean

• 可视化散点图：
  

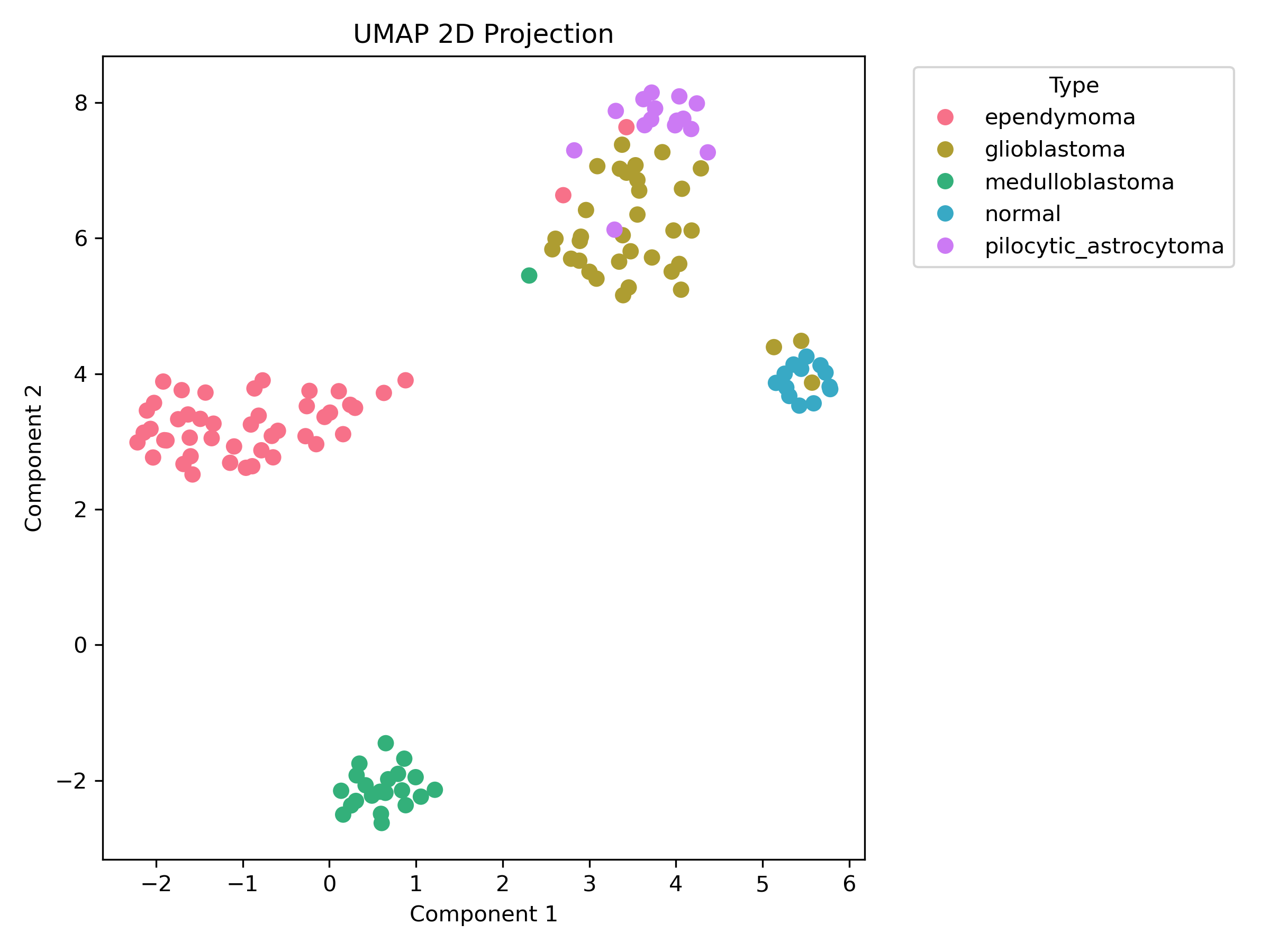
• 时间开销：9.32 秒

• 信任度（trustworthiness）：0.968（相对 PCA 提升 0.025）

• 噪声敏感度：1.1703（特征加入 σ=0.01 高斯噪声）

• n_epochs：0

4.3.5 LLE 降维与可视化

• 使用参数：n_components=2, n_neighbors=15, method=standard

• 可视化散点图：
  

• 时间开销：0.05 秒

• 信任度（trustworthiness）：0.945（相对 PCA 提升 0.002）

• 噪声敏感度：0.0004（特征加入 σ=0.01 高斯噪声）

• reconstruction_error：5.3770877804884595e-05

4.4 降维方法比较

下表从时间开销、非线性结构保留能力、可解释性以及噪声敏感度四个方面总结：

方法	时间开销 (s)	非线性结构保留 (trust)	可解释性 (1-5)	噪声敏感度
PCA	0.07	0.944	5	0.0111
t-SNE	5.82	0.978	2	0.6678
ICA	0.04	0.942	4	0.0016
UMAP	9.32	0.968	3	1.1703
LLE	0.05	0.945	3	0.0004

其中可解释性采用 1-5 评分：线性/可回溯方法（如 PCA、ICA）得分更高，深度非线性嵌入（如 t-SNE）相对较低。噪声敏感度值越小表示对 σ=0.010 的输入扰动越鲁棒。
PCA（主成分分析）分析
PCA在时间开销上表现优异（0.07秒），仅次于ICA，适合处理大规模数据或实时应用。其非线性结构保留能力中等（trust=0.944），但可解释性满分（5分），因输出维度与原始特征线性相关，易于理解与可视化。噪声敏感度较低（0.0111），表明对数据中的轻微扰动不敏感，适合噪声环境下的稳健降维。然而，PCA基于线性假设，对复杂非线性结构的捕捉能力有限，适用于金融数据、图像预处理等要求高可解释性的场景。
t-SNE（t-分布随机邻域嵌入）分析
t-SNE的时间开销最高（5.82秒），计算成本大，仅适合小规模数据或离线分析。但其非线性结构保留能力最强（trust=0.978），能有效可视化高维数据的聚类结构（如生物信息学中的细胞分群）。可解释性较差（2分），因输出为概率分布，难以直接关联原始特征；噪声敏感度高（0.6678），对异常值敏感，需数据预处理。推荐用于探索性数据分析（如单细胞RNA序列可视化），但避免在噪声多或实时系统中使用。
ICA（独立成分分析）分析
ICA是时间效率最优的方法（0.04秒），适合高吞吐量场景（如信号处理）。结构保留能力接近PCA（trust=0.942），但侧重于分离独立源信号，可解释性良好（4分）。噪声敏感度极低（0.0016），对噪声几乎免疫，使其在EEG脑电信号去噪等任务中表现突出。缺点是非线性结构捕捉弱于t-SNE/UMAP，推荐用于盲源分离、实时信号处理等需高速且抗噪声的场景。
UMAP（均匀流形近似与投影）分析
UMAP时间开销最大（9.32秒），但平衡了效率与质量：结构保留能力优异（trust=0.968），接近t-SNE，且可保持全局结构。可解释性中等（3分），输出可部分回溯原始特征；噪声敏感度最高（1.1703），易受异常值影响，需数据清洗。适用于需要高保真可视化的场景（如基因组学或流形学习），但需权衡计算成本。
LLE（局部线性嵌入）分析
LLE时间效率高（0.05秒），与PCA/ICA相当，适合快速降维。结构保留能力中等（trust=0.945），侧重于局部邻域关系，可解释性一般（3分）。噪声敏感度最低（0.0004），对噪声鲁棒性强，但在全局结构保留上弱于UMAP。推荐用于图像降维或物理数据建模，尤其噪声多的环境（如传感器数据）。
总结与推荐
综合性能，推荐如下场景选择方法：

• 高可解释性与效率场景：优先选择PCA（如金融风控、工业监控）。
• 高质量可视化与聚类分析：选择t-SNE（小数据）或UMAP（大数据），但需接受高计算成本（如生物信息学）。
• 实时处理与抗噪声需求：ICA或LLE更优，ICA适合信号分离，LLE适合噪声环境（如实时通信、物联网数据）。
• 平衡效率与结构保留：UMAP为折中选择，但需预处理噪声；LLE适合局部结构重要的任务。

4.5 （选做）基于降维结果的聚类 / 分类评估

对 Brain_GSE50161.csv 先按方差挑选 top 特征并标准化，然后在降维前后运行 KMeans (n_clusters=5).

表示	特征维度	Accuracy	ARI	NMI
ICA	2	0.869	0.744	0.746
LLE	2	0.731	0.553	0.685
Original	200	0.708	0.563	0.691
PCA	2	0.746	0.619	0.704
UMAP	2	0.869	0.766	0.779
t-SNE	2	0.754	0.609	0.743

从结果可见，原始 200 维特征的 KMeans 表现较弱（Accuracy=0.708），而多数降维方法在压缩到 2 维后反而使聚类性能提升，尤其是 ICA 和 UMAP（Accuracy 均达到 0.869）。
这说明原始高维空间包含噪声或冗余信息，不利于 KMeans 使用的距离度量；而有效的降维方法能提取更有区分度的结构，使簇更紧致。
LLE 表现最差，说明它生成的 2D 流形对 KMeans 不够友好。PCA 与 t-SNE 提升中等。
总体结论：合适的降维（如 ICA、UMAP）可以显著改善 KMeans 的聚类效果。

5. 实验心得与总结

通过本次降维实验，我对高维数据的特点以及降维技术的作用有了更直观的理解。实验中可以明显感受到，高维特征中常包含噪声和冗余信息，直接进行聚类往往效果不好，而经过合适的降维（如 ICA、UMAP），数据的结构被重新表达得更加紧凑、更具分离性，使得后续 KMeans 的表现显著提升。
实验的主要难点在于不同降维方法的参数调节，例如 UMAP 和 t-SNE 对学习率、邻居数量较为敏感，初始参数不当会导致可视化结构混乱。我通过多次尝试和参考文档逐步找到较稳定的设置。另一个难点是理解各算法的核心思想，通过对比各方法的输出效果，也帮助我加深了对它们在保持全局或局部结构方面差异的认识。
总体来说，这次实验帮助我建立了从“高维 → 降维 → 可视化/聚类”这一完整的数据分析流程意识，对实际数据处理中降维的重要性也有了更深刻的体会。