关于离散化的若干理解

一、简单介绍

 离散化是一种数据处理的技巧，本质上可以看成是一种哈希其，保证数据在哈希以后仍然保持原来的全/偏序关系。通俗地讲就是当有些数据因为本身很大或者类型不支持，自身无法作为数组的下标来方便地处理（离散化问题的特征），而影响最终结果的只有元素之间的相对大小关系时，我们可以将原来的数据按照排名来处理问题，即离散化。（参考离散化 - OI Wiki (oi-wiki.org)）

二、离散化问题的常见实现步骤

1.思路理解

离散化通过数组下标将稀疏分散的数依据他们的关系映射到另外一个数组中，这样做的好处是能够有效地节省空间，以及方便操作，避免数组有限空间不能存储所有数的问题。而在建立映射关系的过程中我们将原数据理解为一条直线轴上面的许许多多分散的有权点，而映射的建立就是将这些点拉倒一块的过程。例如我们可以看到下面示意图所示的内容：

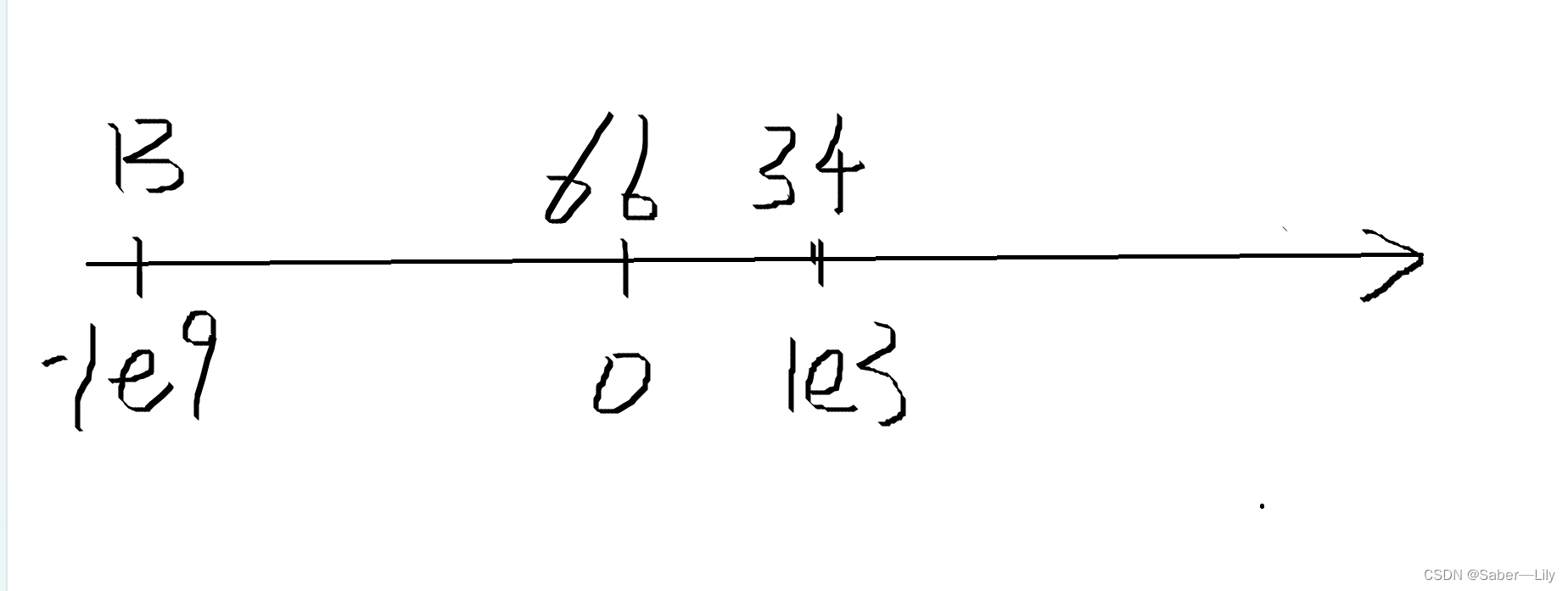
如图所示该组数据的原始坐标分别是-1e9 ,0, 1e3，权值分别是13 ， 66， 34。如果直接用数组来存储该数据是不现实的。此时我们就要用到离散化来进行处理（如下图）：

我们通过离散化将不同下标通过映射装换成可以实现的形式，而新坐标之间的大小关系仍然与原坐标之间的大小关系一样单调递增，并未发生改变，我们根据这一特性，选择二分查找作为新旧坐标映射方式。这样一来，当我们要对原来坐标的权重做处理时我们就只需要通过二分查找就可以找到原坐标对应的新坐标从而进行相关的操作。

2.算法步骤

1.建立一个vector，用其存储原坐标，vector的下标默认为映射后的新坐标；

2.对vector进行排序和去重操作（此时离散化操作已经完成）

3.通过二分查找进行映射查找原坐标对应的新坐标，从而进行一些相关操作。

3.核心代码实现

vector<int>loc;

、、、、、、/*第一部分根据题目的具体情况将原坐标存入loc即可*/

loc.erase(unique(loc.begin(),loc.end()),loc.end());
sort(loc.begin(),loc.end());/*第二部分排序与去重，顺序没有影响*/

、、、、、、/*第三部分根据题目具体情况进行操作*/

三、小结

感觉离散化主要是核心步骤，其他的要多注意细节。