一文读懂蒲丰投针实验

这个博客源于概率论复习期间，蒙特卡罗方法的思想起源，这种求$\pi$的思路非常的巧妙

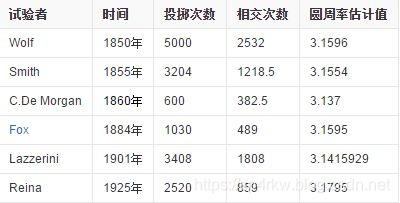
附：历史上用蒲丰投针实验估计圆周率的实验记录，来源

蒲丰投针

蒲丰投针实验是法国数学家、自然科学家“乔治-路易·勒克莱尔·德·蒲丰”在18世纪提出的。
其实验方法极其简单：

• 取出一张白纸，在白纸上画出一组平行等距的直线。
• 将纸平放，任意地向白纸上抛一枚长度为直线间距一半的针
• 多次投针，记录下针与直线相交的次数和总的投针次数，最后相除算出针与直线相交的概率

你会惊奇地发现此概率为圆周率的倒数（1/ π）
蒲丰投针实验是第一个用几何形式表达概率问题的例子。我们可以用这种方法来估计圆周率π

蒲丰投针原理

如图，构造一组平行线，间距为a

随机扔一些棍子（针），长度为l

以左下角这根相交的棍子为例，选取其中点，垂直做线到下方平行线，记长度为x；这个棍子与平行线交角为$\phi$

棍子与平行线相交的要求是
$$x\le \frac{l\ast sin\phi }{2}$$
为什么会这样呢？接下来我们来继续分析。先画一个三角形，斜边为棍子l，下边为上图的平行线（模拟情况是刚刚好与平行线相交）

如果想要下边界与棍子相交，则x必须要小于$\frac{l\ast sin\phi }{2}$，上边界也是同理。这里一定要注意理解x的定义

既然有了这样的一个数学表达式可以把棍子与平行线相交问题转化，接下来我们就可以通过数学方法来求概率了

这里牵涉到概率论最基本的一些求解知识，不做更具体的说明了

接下来我们可以通过面积比来计算概率

而当投掷数量足够大的时候，我们也可以用投掷比来计算概率，近似可以相等

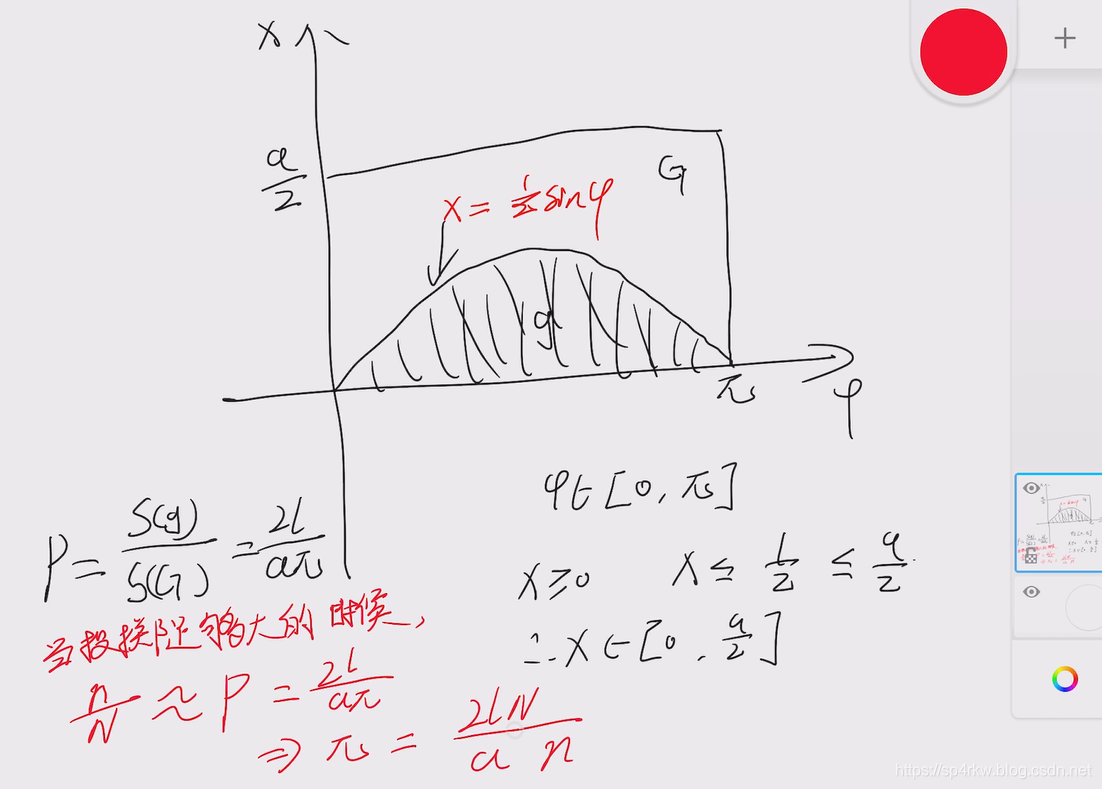
所以，当棍子长度只有平行线间距一半的时候，可以直接用$\frac{1}{\pi }$来代替概率，也就是说$\pi =\frac{1}{p}$

去年写的，才发现没发，丢草稿箱了，hhh