python基础学习：基于蒙特卡洛的蒲丰投针实验模拟求解π近似值

实验问题提出

问题背景介绍

圆周率π 的计算一直是数学界的一个热门话题。自从古代以来，人们一直在尝试用不同的方法计算

π的值，这些方法包括使用几何学、无限级数、积分等等。

蒲丰投针实验是法国数学家、自然科学家“乔治-路易·勒克莱尔·德·蒲丰”在18世纪提出的。其实验方法极其简单：

1）取出一张白纸，在白纸上画出一组平行等距的直线。

2）将纸平放，任意地向白纸上抛一枚长度为直线间距一半的针

3）多次投针，记录下针与直线相交的次数和总的投针次数，最后相除算出针与直线相交的概率。

实验情况如下所示，红色为直线，蓝色为投针（针长度为直线间距一半时）

经过验证发现此概率为圆周率的倒数（1/π）。蒲丰投针实验是第一个用几何形式表达概率问题的例子。我们可以用这种方法来估计圆周率π。以下是网上获取的历史的人重复的蒲丰投针实验数据一览。

由上可见蒲松投针实验可以求出π的近似值。

问题算法解析

以一根直线为例，令针的中点为P，过P作到直线的垂线，与直线交于O点，设OP为X，针所在的直线与等距直线的夹角设为ω，示意图如下：

又令直线间距为d，针长度为l，规定对于一根直线而言，针中点P到直线之间的距离（OP）最大为间距的一半，若大于一半则算作另一根直线的投针，距离（OP）最小为0，若小于0，则算作另一根直线的投针。针所在的直线与等距直线的夹角ω最大为π ，最小为0。

又由于伯努利大数定律，在N重伯努利实验中，在实验次数足够大的条件下,其中某一事件发生的频率n/N可无限接近其发生的概率，可用频率近似估计来代替概率。因此可以重复多次投针实验计算出最终的概率，求得圆周率计算公式如下：

以上就是蒲丰投针实验的算法解析。

问题模拟方法探究

由于蒲丰投针实验，在投针过程当中会受到风力，针的不同，抛出高度，抛出力度等自然或人为因素，实验会存在误差，除此之外再重复投针过程中，极其耗时费力。

蒙特卡罗方法又称统计模拟法、随机抽样技术，是一种随机模拟方法，以概率和统计理论方法为基础的一种计算方法，是使用随机数（伪随机数）来解决很多计算问题的方法。将所求解的问题同一定的概率模型相联系，用计算机实现统计模拟或抽样，以获得问题的近似解。

对比人工实验之下，结合计算机模拟实验速度快，误差小，我准备采用python语言结合蒙特卡洛算法对蒲丰投针实验进行模拟，模拟方案设计见下文。

实验方案设计

蒙特卡洛投针模拟方法设计

1.    for i in N_:
2.        pi_sum = 0
3.        for k in range(Times):
4.            p_num = 0
5.            for j in range(i):
6.                x = random.uniform(0, d / float(2))
7.                omega = random.uniform(0, math.pi)
8.                x_tip = x - float(l) / float(2)math.sin(omega)
9.                if x_tip < 0:
10.                    p_num += 1
11.            p = float(p_num) / float(i)
12.            pi__=(float(2) * l) / (float(d) * p)
13.            pi_sum=pi_sum+pi__
14.        pi_=pi_sum/Times

规律探究算法方案设计

• 为了减小实验的偶然性，使用Times变量重复多次实验，当重复次数大于500时，做出箱线图，观察是否有异常值，再通过3sigma法则去除异常值，求取出Times次重复试验的平均值作为最后的π。
• 为了验证伯努利大数定律，使用多个N值重复投针实验，并做出散点图。观察其变化，并分析数据序列。

实验过程模拟

本文利用python程序对实验进行模拟，为了减少实验用时，采用multiprocessing库中的ThreadPool类的imap方法，实现并行计算，此外利用python中的random库，任意在X，ω样本空间中选取一个随机值（伪随机值），接着用附录中的代码进行实验的模拟，最后调用matplotlib中的plt用法，做出散点图与箱线图，直观分析数据，实验模拟结果分析如下。

数据统计分析

基于Python的蒲丰投针重复实验模拟结果数据分析

本文使用ThreadPool中的imap方法，设置25个并行池对实验进行并行模拟，此外每个池中设置200次重复试验，每次实验投针100000次，最终得出5000个模拟π值，绘制散点图如下所示：其中红色线为标准π值

可见结果大部分汇聚在标准π值两侧，此外对实验结果绘制箱线图如下所示：其中，箱子的中间的线为数据的中位数。箱子的上下底，分别是数据的上四分位数（Q3）和下四分位数（Q1），这意味着箱体包含了50%的数据。因此，箱子的高度在一定程度上反映了数据的波动程度。上下边缘则代表了该组数据的最大值和最小值。箱子外部会有一些点，为数据中的“异常值”。

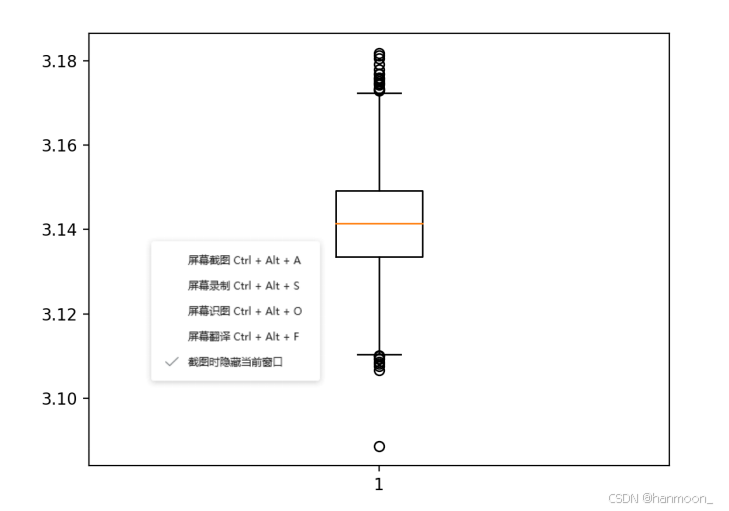
由于该模拟π值序列符合正态分布，可以根据3sigma法则发现随机误差以外的粗大误差，并将其去除，提高结果的准确性。

因此为了减小偶然性，我利用3sigma法则判断异常值并去除，得出结果，模拟π值为3.1415062496074363，误差为8.64039823569307e-05，比较接近标准pi值，结果表现良好。

不同投针次数下蒲丰投针实验的结果数据分析

为了验证伯努利大数定律，使用多个N值重复投针实验，并做出散点图。实验π值随投针次数N变化结果展示如下：

由此可以发现随着投针次数的增加，模拟π值越来越接近相对准确值，为了更直观的展示π误差随着N投针次数的变化，做出误差随N值变化散点图如下：

该图可直观的发现，在N重伯努利实验中，在实验次数足够大的条件下,其中某一事件发生的频率n/N可无限接近其发生的概率，可用频率近似估计来代替概率。概率具有稳定性。当N为2000000000时，模拟π值为3.14158738504382，与标准π值的误差为5.268545973269312e-06。结果较为准确。

实验结果总结

有上述实验可以得知，蒲丰投针实验可以很好的求解出π值近似值，上述实验模拟成功探究了两个问题：

1. 基于蒙特卡洛的蒲丰投针实验中，重复Times次，当Times足够大时，可以通过求算数平均值的方法求解出更加准确的概率值，并且可以使用3sigma法则减弱重复过程中带来的偶然误差。
2. 基于蒙特卡洛的蒲丰投针实验中，重复N次投针，在较小阈值内，N值越大，频率整体上越接近实际概率，符合伯努利大数定律，但是N阈值足够大时，会受到一些实验客观因素如算法精度等，无法趋于最终的实际概率。

此外，在实验过程中我发现，在模拟投针时，我使用了标准π值，以此求积分求解出最终的模拟π值，这是源于该实验是基于自然规律为前提开展的实验，求解最佳π值存在限制。

本次实验受益匪浅，我复习了概率论的相关知识，联合概率密度，大数定律等知识。