使用定义判断函数的奇偶性

题目

判断函数 $f(x)=ln(x+\sqrt{1+x^2})$ 的奇偶性。

解析

本题用到的知识点

$lo{g}_a(MN)=lo{g}_{a}M+lo{g}_{a}N$

在 MATLAB (下面的代码在 MATLAB 9.1.0.441655 (R2016b) 中测试通过) 中输入如下代码：

x=0:0.01:10;
semilogy(x,log(x))

可以绘制出 $y=ln(x)$ 的图像：

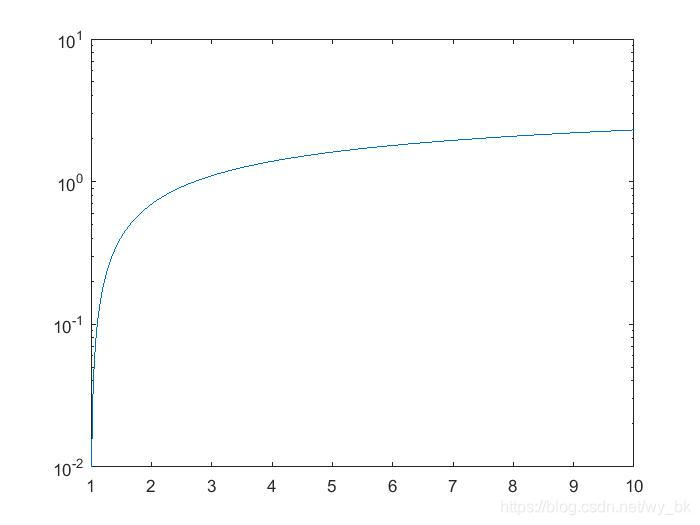
图 1

有图像可以看到，自然对数 $ln(x)$ 只在 $(0,+\infty )$ 的区间里有定义，不符合对数函数或者偶数函数对于“定义域 $X$ 关于原点对称”的要求。不过题目中的函数可以看作是一个符合函数，因此，我们还需要结合 $g(x)=x+\sqrt{1+x^2}$ 的定义域来确定 $f(x)$ 的定义域。

因为：

$\sqrt{1+x^2}>\sqrt{x^2}>|x|>0$

则：

当 $x\in (-\infty ,+\infty )$ 时 $x+\sqrt{1+x^2}>0$ 满足自然对数函数 $ln(x)$ 对定义域的要求，而且，当 $x=0$ 时，$f(x)=ln(1)=0$, 也满足奇函数“当f(x)在原点处有定义时，f(0)=0”的要求。

到这里，定义域的问题解决了，下面要解决的是函数是关于 $y$ 轴对称，还是关于原点对称的问题。

由于：

$f(x)=ln(x+\sqrt{1+x^2})$

$f(-x)=ln(-x+\sqrt{1+x^2})$

则：

$f(x)+f(-x)=ln(\sqrt{1+x^2}+x)+ln(\sqrt{1+x^2}-x)=ln[(\sqrt{1+x^2}+x)(\sqrt{1+x^2}-x)]=ln(1+x^2-x^2)=ln(1)=0$

上面的运算结果符合奇函数的定义，因此，$f(x)=ln(x+\sqrt{1+x^2})$ 是一个奇函数。

此外，使用 WolframAlpha 画出的函数 $f(x)=ln(x+\sqrt{1+x^2})$ 的图像如下：

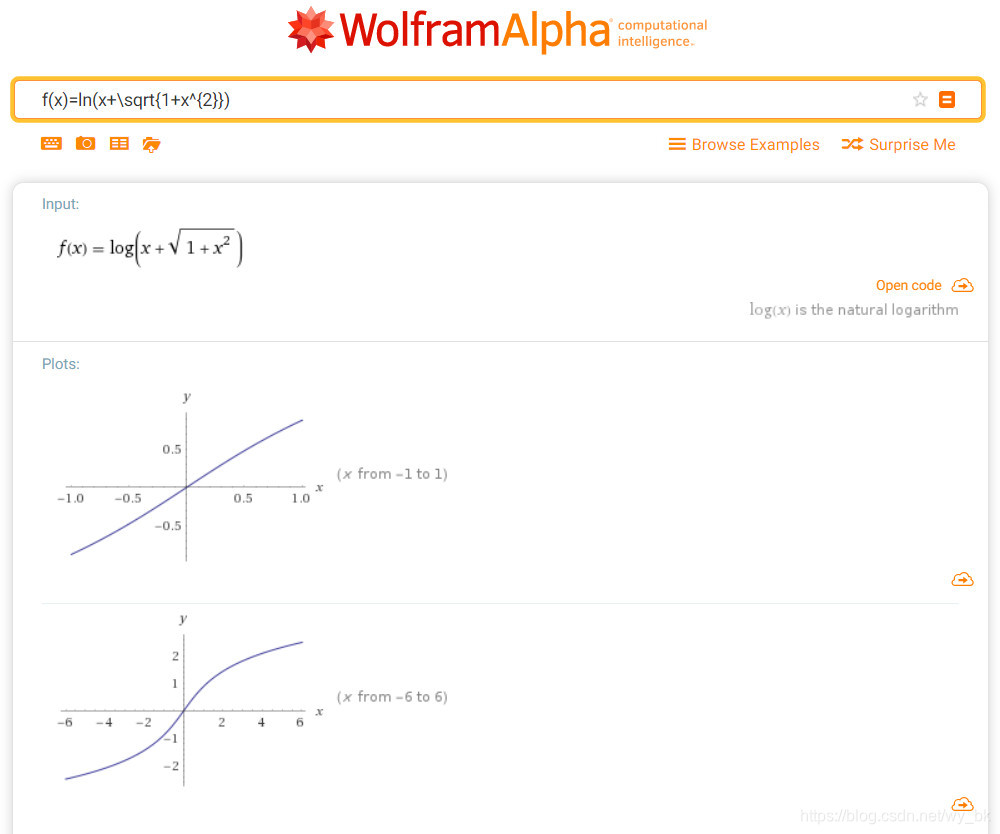
图 2. 图片来自 https://www.wolframalpha.com/

由图像我们也可以看出这是一个奇函数。

EOF