高斯消元学习笔记

先来安利一个博客 高斯消元 & 线性基【学习笔记】
本文就讲了最基础的高斯消元，高斯消元的扩展应用可以看上面的那个呀w

---

高斯消元是用来解线性方程组的。所谓线性方程组，就是一次方程组。
对于解这个一般的线性方程组，求 xi：

a11 * x1 + a12 * x2 + ... + a1n * xn = b1
a21 * x1 + a22 * x2 + ... + a2n * xn = b2
...
an1 * x1 + an2 * x2 + ... + ann * xn = bn

同时，我们顺便定义一下矩阵乘法。设 A 为 m * p 的矩阵，B 为 p * n 的矩阵，那么称 m * n 的矩阵 C 为矩阵 A与 B 的乘积，那么有 $(A×B)_{ij} = \sum_{k=1}^p A_{ik} B_{kj}$。
从这里得到启发，可以定义系数矩阵、未知数矩阵以及等式右边的常数矩阵 $A$、$x$ 和 $B$。那么根据矩阵乘法，我们可以将这一共 n 个等式极为简单地描述为一个等式，即 $Ax = B$。

=

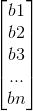
我们将上述矩阵变为增广矩阵：

我们需要一个n 行 n + 1 列的数组来存
多出来那一列就是常数矩阵 $B$

–

for (int j = i + 1; j <= n; j ++) {
    double t = M[j][i] / M[i][i];
    for (int k = i; k <= n + 1; k ++) M[j][k] -= t * M[i][k];
}

这是用第 i 个方程去消第 i + 1 ~ n 个方程，通过调整第 i 个未知数的系数，来消掉后面那些方程中的这个第 i 个未知数
所以 double t = M[j][i] / M[i][i]; 除的是 M[i][i] 。
j 是要被消的方程，k 是被消的方程的第几项

举个例子比如 n = 3 时：

a11 * x1 + a12 * x2 + a13 * x3 = b1
           a22 * x2 + a23 * x3 = b2
                      a33 * x3 = b3

–

消完以后，矩阵变成这样的上三角矩阵：

（用最右边应该还有一列常数项，注意常数项也要消元

然后直接回代即可。从下往上循环，每一次可以确定一个变量，然后将其上面的所有行给代进去，将相应的系数变成 0，方程式右边的常数项也相应地减去相应的量。

接着上面的那个例子：

a11 * x1 + a12 * x2 + a13 * x3 = b1
           a22 * x2 + a23 * x3 = b2
                      a33 * x3 = b3

这时候可以解出 x3，然后带到前面的每个方程里，就变成：

a11 * x1 + a12 * x1 = b1 - x3 * a13
           a22 * x2 = b2 - x3 * a23

然后解出 x2，继续做下去
最终就全解出来了

for (int i = n; i >= 1; i --) {
    M[i][n + 1] /= M[i][i];
    M[i][i] = 1;

    for (int j = 1; j <= i; j ++) {
        M[j][n + 1] -= M[i][n + 1] * M[j][i];
        M[j][i] = 0;
    }
}

这就是带回去的过程
最终 M[i][n] 就是第 i 个未知数的解，因为第 i 个方程是 xi = k 的形式

–

int k = i;
for (int j = i + 1; i <= n; i ++)
    if (fabs(M[j][i]) > fabs(M[k][i])) k = j;

if (k != i) for (int j = i; j <= n + 1; j ++) swap(M[i][j], M[k][j]);

这段是找当前项（当前列）系数绝对值最大的一个方程，并与当前行交换，可以保证精度，在消元的时候把浮点数的误差降到最小。

–

这就是高斯消元法。其的时间复杂度其实是相当好估计的。每一次先选择两行，再将这两行开始消元，于是每一次消元需要枚举每一个矩阵中的变量，所以就是 $O(n^2m)$，是立方级的。

inline void gauss(int n) {
    for (int i = 1; i <= n; i ++) {
        int k = i;
        for (int j = i + 1; i <= n; i ++)
            if (fabs(M[j][i]) > fabs(M[k][i])) k = j;

        if (k != i) for (int j = i; j <= n + 1; j ++) swap(M[i][j], M[k][j]);

        for (int j = i + 1; j <= n; j ++) {
            double t = M[j][i] / M[i][i];
            for (int k = i; k <= n + 1; k ++) M[j][k] -= t * M[i][k];
        }
    }

    for (int i = n; i >= 1; i --) {
        M[i][n + 1] /= M[i][i];
        M[i][i] = 1;

        for (int j = 1; j <= i; j ++) {
            M[j][n + 1] -= M[i][n + 1] * M[j][i];
            M[j][i] = 0;
        }
    }
}