最优性原理:无论过程的初始状态和初始决策是什么,其余决策都必须相对于初始决策所产生的状态构成一个最优序列。
在我的理解就是:对于你的决策答案,一旦确定它是最优的,那么你的答案中的一部分肯定是最优的。
关于动态规划的很多证明都是按照这个,用反证法,如果不是这样则不符合最优性原理。。贪心方法也是,我既然是贪心方法,那么只要是满足我的贪心条件
就必须拿过来,不然你就不是贪心方法。
----------------------------多段图--------------------------------------------
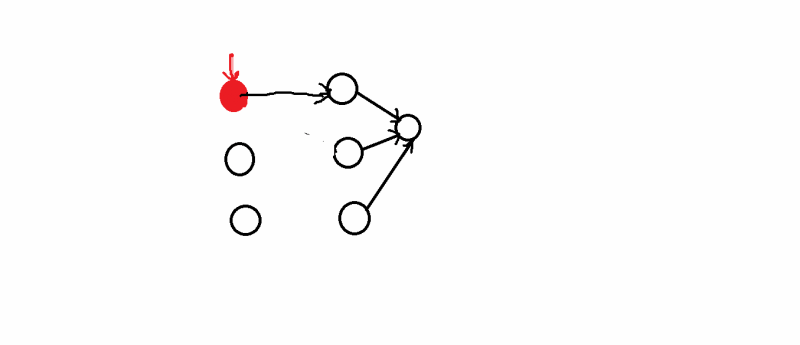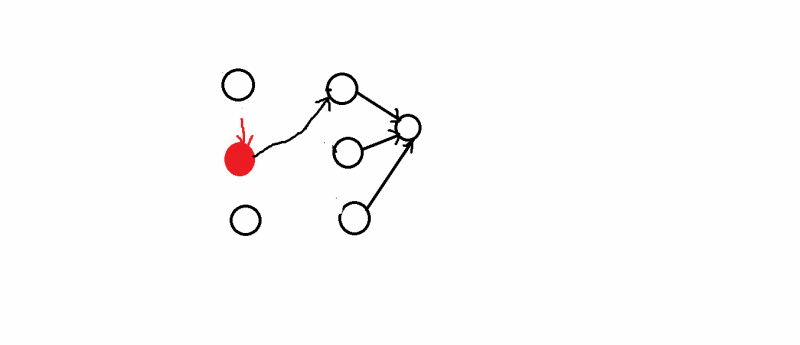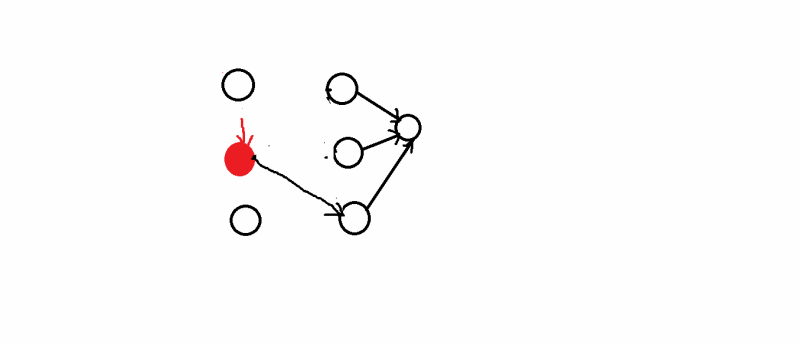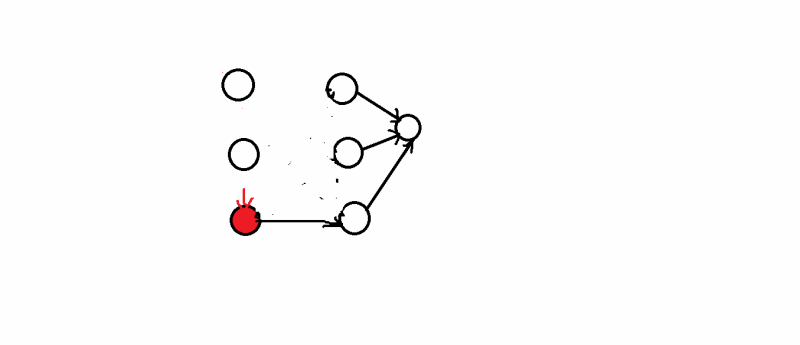
向前处理法:
从后往前处理,这是根据最优性原理,从后面入手,一步一步往前推,对于每个点取min,
向后处理法:
---------------------------------------------------------------------------------------------------------
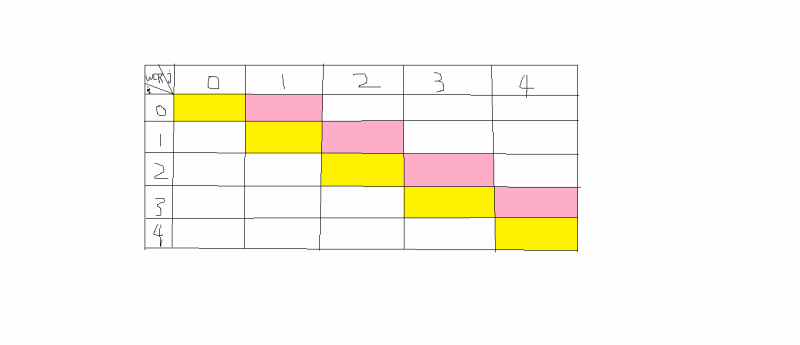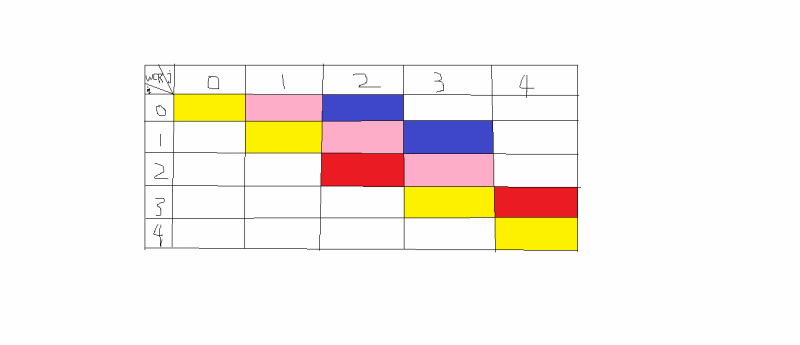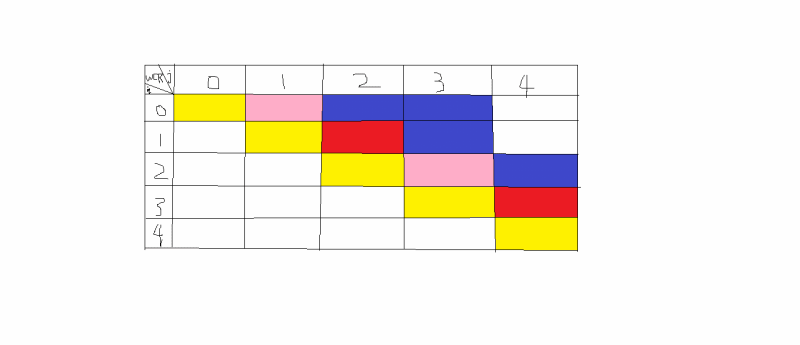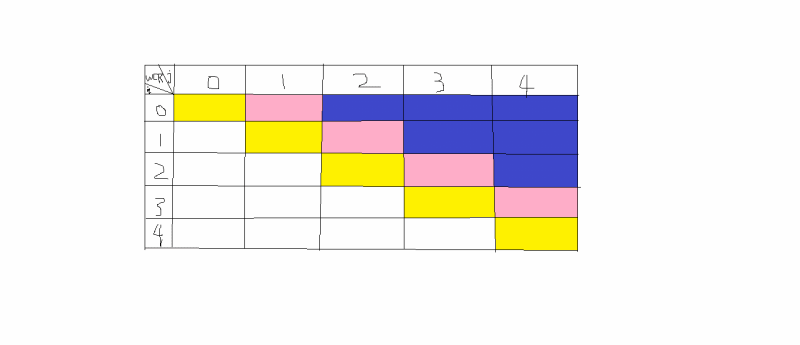
-------------------------------每对节点间最短路径------------------------------
算法中心:以路径中经过的节点为突破口,A的右上角字母K代表路径经过的标号最大的节点。
通过经不经过k讨论,一是经过,则有An(i,j)=An-1(i,k)+An-1(k,j)
二是不经过,则有An(i,j)=An-1(i,j);两者取min,完成递推,又根据最优性原理。可得算法。
两点间最短路径矩阵A(Ak(i,k)=Ak-1(i,k)Ak(k,j)=Ak-1(k,j)故k行k列不动)
算法
更新条件:在那一点的一行中的一个元素,和一列中的一个元素和小于该点值,更新!注意,那两点为(i,k)(k,j)形式。
关于保存路径矩阵P(记录的是下一个即j)
当A更新时,P同步更新下一点,将更新处值改为上面的k。
疑惑:
标记处的条件必须吗?
算法为三重循环k,i,j
当k=2,时进去循环i=1,j=1
这均小于k,也继续计算啊····
----------------------最优二分检索树-------------------------











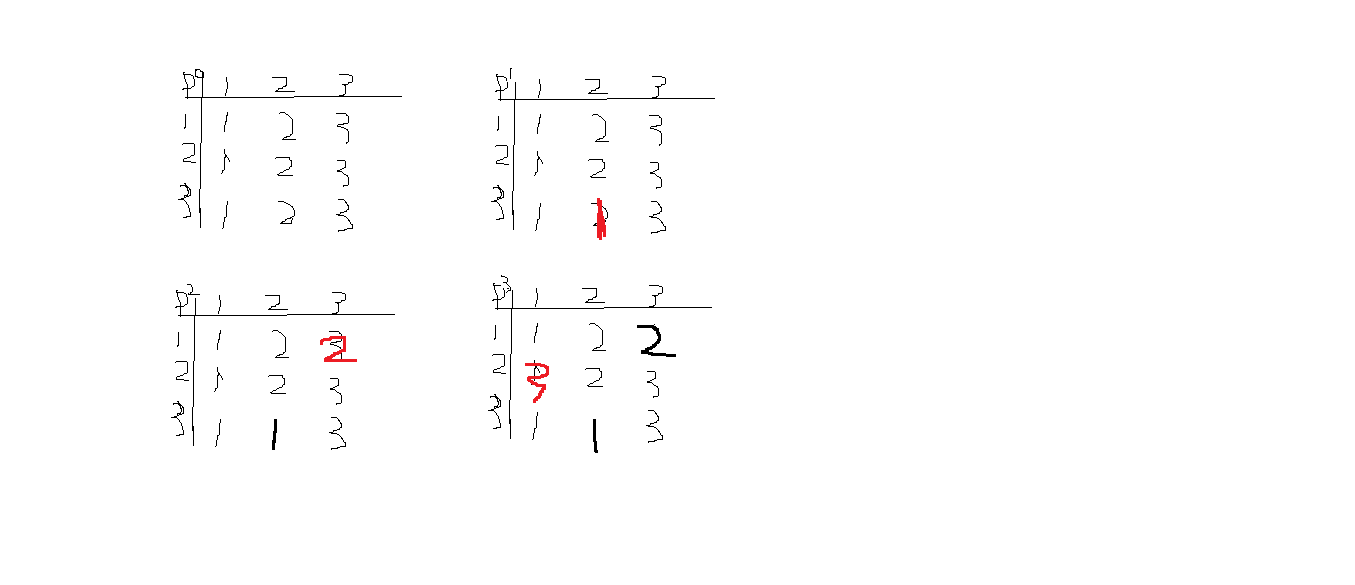















 6964
6964

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








