题目意思:
给出N,K。N代表有N个人,N个人手中每个人都拿了一张卡号,会给出N个人的姓名和他们手中所持卡片的卡号。
给出的K,代表第一次第K个人出局,然后下一个出局的人与当前出局的人手中所持有的卡片上的数字有关。
如果这个数字A是大于0的,代表从当前出局人数的左手边往右数第A个人出局,如果这个数字A小于0,代表
从右手边往左数第A个人出局。如果以右为正方向,就是题中所描述的右手边-Ath人出局。由于每个出局的
人都可以获得一定的糖果数量,所得糖果数量的规律是,第num个出局的人,他所获得的糖果数是num因子的
数量。让求获得糖果数量最多的那个人的姓名和糖果数量。如果最多糖果数对应多个人,则输出的答案是最先
出局的那个人的姓名。
这个题目很难,以前做过名字叫变态杀人狂的题目,就是有n个人,编号为1~n,数到m的人被杀,问最后出局的人
的编号,大一的时候做这个题目,直接就是模拟,现在才知道经过数学的推导是可以直接得到下一个被杀人的编号
的。POJ题目数据范围普遍都偏大,模拟这去淘汰人不现实,更何况每出局一人,其指定的下一个出局的规则还在
不停的变。到现在才知道约瑟夫环,一直知道这种问题,但是不知道这种问题属于约瑟夫环。
线段树专题做到这个题目,感觉真的搞错了,这怎么去线段树,完全不知道怎么线段树。
也是借助了别人的思路,反素数+线段树+约瑟夫环。
难点1:第num个出局的人获得糖果数是num的因子个数,对于一个数N,我们要知道1~N中所有数的因子个数,然后找最大的那个人。
但是这样很耗时,就要借助反素数来求解。
反素数的定义:对于任何正整数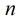
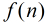
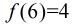
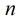
数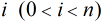
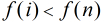
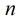
一个数是反素数,假如它是number,说明在1~number里面,number的因子个数最多,
证明如下:如果number是反素数,则(0<i<number) i的因子个数<number的因子个数 (这时反素数的定义)
假如存在(0<i<number) i的因子个数>=number的因子个数,则0~num中的数是反素数,根据定义number不是反素数。
所以我们要制作反素数表,n的范围是5000000,则我们就先求1~500000中每个数的因子个数。
设当前因子的最大个数为mmax,如果mmax小于数字number的因子个数,则更新mmax,number就是反素数,我们存储他,并将他对应的因子个数存在
另一个数组中。有了反素数表以及其所对应因子个数的表,则就能减少循环次数,快速查询到N个人的游戏,第几个人出局时得糖果数最多,同时也就
知道了出局时获得糖果得个数,因为我们用另一个数组存储了对应得个数。
难点2:知道当前未出局得人数为n,还知道要让当前序列中第k个人出局,如何得知下一个要出局得人在n-1人的序列中是第几个人。
看了好多人的博客,形形色色的推导式子都有,都略有不同,但是没有一个人解释如何推导,感觉大神都总是这样,只给结论不给推导,、
我自己推的时候都晕死在约瑟夫环里面了,转来转去都不知道转到哪了。刚开始题目意思也没理解对。好在后来推出来了,现在就来推导人的序号。
假如当前剩余n个人,第k个人出局,然后对剩余n-1个人从左到右编号后,
如果A>0,则下一个出局的人在新序列中的编号为 k = ((k-1+A)%(n-1)+n-2)%(n-2)+1; ///或k = (k-1+A-1)%(n-1)+1;
如果A<0,则下一个出局的人在新序列中的编号为 k = ((k-1+A])%(n-1)+n-1)%(n-1)+1;
现在来推导这两个公式:
假设当前剩余n个人,第k个人出局,n个人的编号是从0~n-1的。则整个序列如下:
考虑A<0的情况:
3.如何构建线段树,如果每次我们都能通过n个人中删除第k个人,推导下一个被删除的人再n-1个人序列中的编号,这个编号就是它再n-1个人中,从最左边开始数,它
排第几个,因此可以构建规模1~n的线段树,记录区间中还活着的人数,每次计算出k之后,就知道这个人再剩余序列中是第几个人,将这个人插入到线段树中,代表这个
人已经死了。已知k,如果k<(根节点左区间的剩余人数,再左子树中查找),否则k-根节点左区间中剩余的人数,再在右区间中查找。
这个题目并不需要把所有人都插入线段树,值需要利用反素数表,求得第几个出列的人获得糖果最多,然后在线段树中插入这么多人就好了,可以插入并返回被杀人在最
原来n个人的序列中的编号,这样比较节省时间,仅仅需要对查询的函数略作改进即可。
AC代码:
#include <iostream>
#include <stdio.h>
#include <string.h>
#define lchild left,mid,root<<1
#define rchild mid+1,right,root<<1|1
using namespace std;
const int maxn = 560000;
/**500000内最大的反素数是498960,但是要多求一位,如果一个数比498960大,肯定会去和下一个反素数比较,
不多找一位的话会RE,下一个反素数是55XXXX,所以maxn开到560000**/
int yinzi[maxn];
int a[]={1,2,4,6,12,24,36,48,60,120,180,240,360,720,840,1260,1680,2520,5040,7560,10080,15120,20160,25200,27720,45360,50400,55440,83160,110880,166320,221760,277200,332640,498960,554400}; ///存放反素数
int b[]={1,2,3,4,6,8,9,10,12,16,18,20,24,30,32,36,40,48,60,64,72,80,84,90,96,100,108,120,128,144,160,168,180,192,200,216}; ///存放a表中对应反素数的因子个数
int num;
char name[maxn][13];
int A[maxn];
/**先求反素数表,然后输出到文件,直接把表制作出来,就像上面,
不过这个题,直接放这个双层for循环提交也不会超时,这个试过了,
不过看到n有点大,把求出来的结果直接输到文件制表,更保险
void create_table()
{
FILE *f1,*f2;
f1 = fopen("text1.txt","a");
f2 = fopen("text2.txt","a");
fprintf(f1,"{");
fprintf(f2,"{");
for(int i = 1;i < maxn; i++)
for(int j = i; j < maxn; j += i)
{
yinzi[j]++;
}
num = 0;
int mmax = 0;
for(int i = 1; i < maxn; i++)
{
if(mmax<yinzi[i])
{
mmax = yinzi[i];
a[num] = i;
b[num] = yinzi[i];
fprintf(f1,"%d,",i);
fprintf(f2,"%d,",mmax);
//printf("{反素数:%d,因子个数:%d}\n",i,mmax);
num++;
}
}
fprintf(f1,"}");
fprintf(f2,"}");
fclose(f1);
fclose(f2);
}
**/
int sum[maxn<<2]; ///所包含区间的剩余活着的人数
void push_up(int root)
{
sum[root] = sum[root<<1]+sum[root<<1|1];
}
void build(int left,int right,int root)
{
sum[root] = right-left+1;
if(left == right) return;
int mid = (left+right)>>1;
build(lchild);
build(rchild);
}
int query(int pos,int left,int right,int root)
{
if(left == right)
{
sum[root] = 0; ///该人踢出去
return left; ///返回再原序列中的编号
}
int mid = (left+right)>>1;
int ans;
if(pos <= sum[root<<1]) ans = query(pos,lchild);
else ans = query(pos-sum[root<<1],rchild);
push_up(root);
return ans;
}
int main()
{
int n,k;
//create_table(); ///先打表
while(~scanf("%d%d",&n,&k))
{
for(int i = 1; i <= n; i++)
{
scanf("%s%d",name[i],&A[i]);
}
int ans=0;
while(a[ans]<=n) ans++;
ans--; ///则第a[ans]个出队的人所获得的糖果数量最多
build(1,n,1); ///构建线段树
int temp = a[ans]; ///一会儿寻找第temp个出局的人就是得到糖果最多的人。
int index;
while(temp--)
{
index = query(k,1,n,1); ///完成杀人并返回被杀人在原始序列中编号的操作
//printf("所剩余人数是%d\n",sum[1]);
//printf("出局的人是 %s\n",name[index]);
if(sum[1] == 0) break;
/**小心,就像题目所给测试数据,最后一个出局的人最多,此时所剩余人数是0,
不能在求下个人的位置了,否则会发生除0错误,导致程序不能运行**/
if(A[index]>0)
k = ((k-1+A[index])%sum[1]+sum[1]-1)%sum[1]+1; ///或k = (k-1+A[index]-1)%sum[1]+1;
else
k = ((k-1+A[index])%sum[1]+sum[1])%sum[1]+1;
///sum[1]是1节点,其含义是1~n这个区间内还活着的人数
}
printf("%s %d\n",name[index],b[ans]);
}
return 0;
}
























 778
778

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








