03-快速排序时间复杂度论证

证明过程中涉及到一些数学公式，

 表示连加求和， i 表示的就是 i = 1 + 2 +3 + .....+ n。

E(X)是数学期望，也表示均值，离散型随机变量E(X) =  （代表具体值，该值出现的概率）。

期望的运算性质：

1. E(c) = c 。c是常数
2. E(cX) = cE(X)。
3. E(X+Y) = E(X) + E(Y)，E(X-Y) = E(X) - E(Y)，E(X*Y) = E(X) * E(Y)。

快速排序的时间依赖于划分是否平衡，而划分是否平衡依赖于划分的元素，如果划分是平衡的，则性能跟归并排序一致，如果划分不平衡，则性能接近插入排序。

最坏情况分析

当划分的两个子问题分别包含n-1个元素和0个元素时，假设每一次调用都出现了这种不平衡划分，划分操作的时间复杂度是(n)，由于对一个大小为0数组进行递归调用会直接返回，T(0) = (1);

算法的运行时间的递归式可以表示为：T(n) = T(n-1) + (n);

T(n)= T(n-1) + (n)= T(n-2) + (n) + (n)= T(n-3) + (n) + (n) + (n)= T(1) + n (n) = ()

在最坏的情况下，快速排序的时间复杂度为 ()。此外，当数组完全有序时，快速排序的复杂度依旧为()，插入排序的复杂度为O(n)。

最好情况分析

在可能得最平衡的划分下，两个子问题的规模是差不多相同的。

算法运行的时间表达式为：T(n) = 2 * T() + (n)。

这个符合递归的master公式，a = 2, b = 2, d = 1,当  = d 时，复杂度为O(* ) 。

在最好的情况下，快速排序的时间复杂度为(nlgn)。

平均情况的直观观察

a中显示出现了一个坏的划分，下一层中是一个好的划分，b中出现的是好的划分，a中出现的待解决的问题规模并不比b中的问题规模大。因此当好的情况和坏的情况交替出现时，快速排序的时间复杂度与全是好的情况下是一样的为O(nlgn)。

期望运行时间

       对于有n个元素的数组来说，划分的次数最多是n次，假设每次划分过程中比较的总次数为X，那么快速排序的运行时间为O(n+X)。

       目标是计算出X，因此需要了解什么时候对数组中的两个元素进行比较，什么时候不比较，为了便于分析，定义： = {,, ..., }.

定义一个指示器随机变量：   = I{与进行比较}。

       我们考虑的是比较操作是否在算法执行过程中任意时间发生，而不是局限在某一次循环是否发生，每一对元素最多比较一次，因为每个元素只会跟主元元素(划分的元素)进行比较，在某一次划分结束后，主元元素则不会再参加比较。所以很容易刻画出总比较次数：X = 。

对上式两边取期望，再利用期望的线性特性可以得到：

E(X) = E() =  E()​​​​​​​ =   {与进行比较}  。

上式中的{与进行比较}需要进一步计算，在我们的分析中，假设随机且独立的选择主元。

首先看两个元素不会进行比较的情况是根据主元划分左右数组后，左边的元素不会再跟右边的元素进行比较，那么两个元素会进行比较的情况是两个的其中一个被选为主元，集合中有（j-i+1）个元素，那么每一个元素被选择的概率为1/(j-i+1)，于是就有：

E(X) =  {与进行比较}  =   

将k = j - i 代入

E(X) =   =   <   < (2)< 2(n−1)lnn

所以时间复杂度为O(n)。

---

指示器随机变量

它为概率和期望之间的转换提供了一个便利的方法，给定一个样本空间S和一个事件A，那么事件A对应的指示器随机变量为

                    

接下来定义一个指示器随机变量，对于硬币正面朝上的事件记作H，表示抛硬币时正面朝上的次数，如果正面朝上则值为1，否则值为0。则可以记成

               

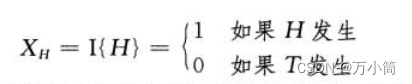
在一次抛硬币中，正面朝上的期望次数就是指示器变量的期望值：

E[] = E[ I{H} ] = 1 * Pr{H} + 0 * Pr{}  = Pr{H} = 1 * 1/2 = 1/2。

综上可得设 = I{H} ，就有() = Pr{H}。