目录
1.原理
经过几天的折磨,终于是把目前遇到的问题全部解决了。下面我主要讲一下我觉得比较关键的两个点。一个是采样的问题一个是适用条件的问题。其实参考文献中都已经讲的比较清楚,只是本人没有认真阅读【汗颜】。话不多说把调试好的代码奉上,开始

总的算法可以分成是上面两类,冲击响应和角谱(这里的单次傅里叶算法不知道能不能算作角谱)。具体算法的由来和分类可以看参考文献1,2。两位大佬讲的是非常好【👏】。
1.1傅里叶变换中的分辨率问题
首先看看对二维图像做傅里叶变换后的图像的分辨率和范围到底是怎么确定的,关于这个问题我们首先给出一个一维的离散坐标系。表示离散的坐标轴,这个坐标轴是有实际的物理尺寸的。如下,这里取x方向分析,y方向是一样的。
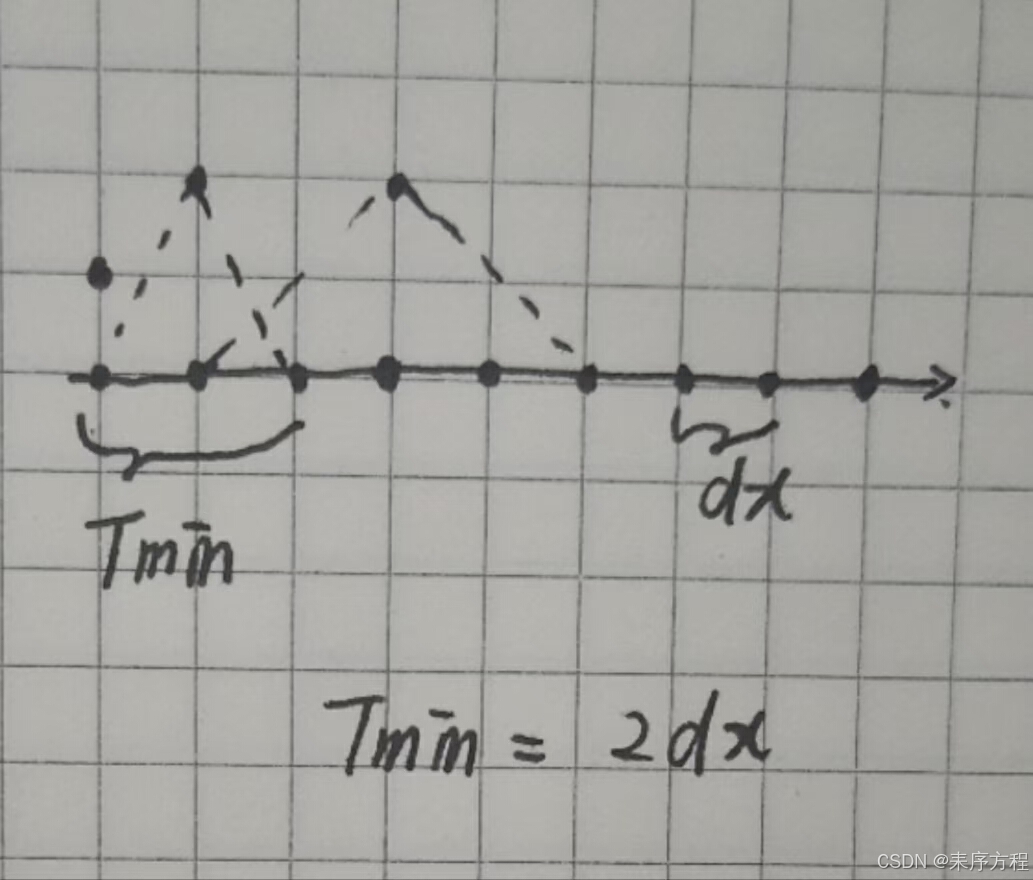
在这么一个坐标轴下,你能找到的最小周期Tmin = 2*dx,这里dx是空间频率的分辨率。那么这时候更具频率和周期的关系,以及假定频率采样点和空间采样点一致。可以得到空间频率的范围和采样率。
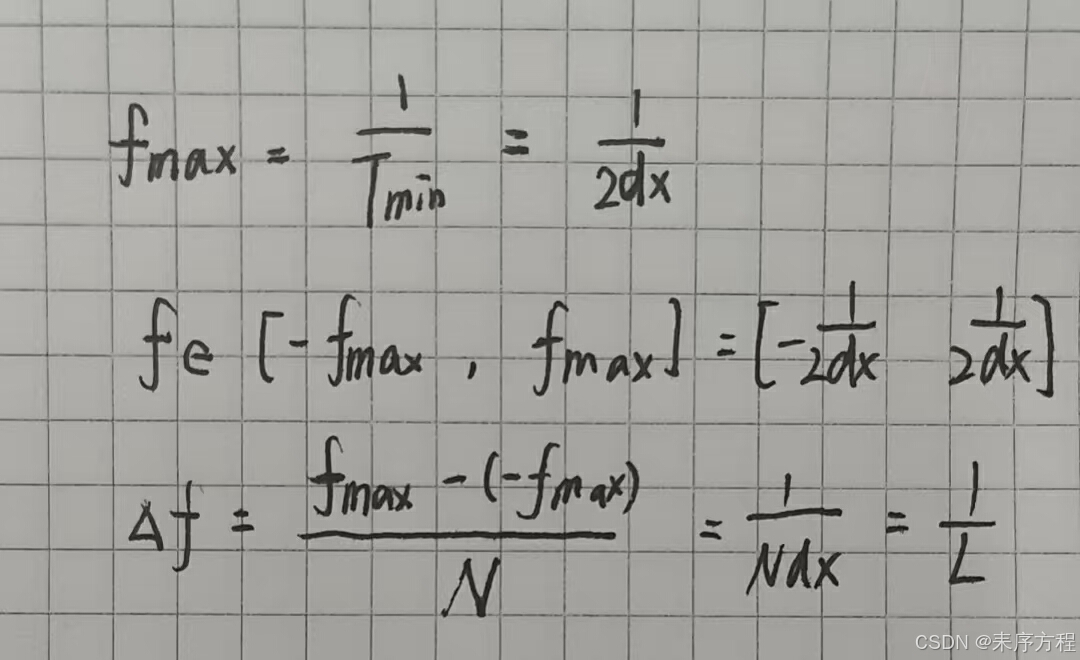
那么通过上面的这两个公式,就可以得到以下两个结论:
1.对原图像补零,L增大->detaf减小,可以得到更高的空间分辨率
2.对信号上采样,采样点数增加但是空间的尺寸不变,也就是空间分辨率dx减小。fmax增大也就是得到了更大的频率范围
读到这里,读者可以思考一下为什么冲击响应的方式可以只计算局部而角谱却必须计算整个和光源平面一样的范围(作者认为:角谱上的每一个频率分量都是光源平面上每一个点的映射)
1.2角谱算法和冲击响应积分的适用条件
这里参考2给了详细的推导,我这里直接剽窃结论


代码里面可以使用,两个条件的交集对应的传播距离,这样可以兼顾两种类型的方法。
d = np.sqrt((deta*L0/lambda_)**2-0.25*(L0**2)) # 传输距离,单位米
f = d2.参考代码
下面是完整的代码,读者可以自己跑一下。
import numpy as np
import time
import matplotlib.pyplot as plt
from fanc import *
# 参数设置
lambda_ = 1.064e-6 # 波长,单位转换为米
k = 2 * np.pi / lambda_ # 波矢大小
N0 = 1024 # 入射面采样点数
N = 512 # 出射面采样点数
L0 = 60*1e-3 # 入射面尺寸,单位转换为米
L = 60*1e-3 # 出射面尺寸,单位转换为米
w = 1*1e-3
n = 6
ll = 5*1e-3
deta = L0/N0
d = np.sqrt((deta*L0/lambda_)**2-0.25*(L0**2)) # 传输距离,单位米
f = d
# 离散化入射平面和出射面
x0 = np.linspace(-L0/2, L0/2, N0)
y0 = np.linspace(-L0/2, L0/2, N0)
X0, Y0 = np.meshgrid(x0, y0)
x = np.linspace(-L/2, L/2, N)
y = np.linspace(-L/2, L/2, N)
X, Y = np.meshgrid(x, y)
dx0, dy0 = np.gradient(x0)[0], np.gradient(y0)[0]
T = {}
# 生成光源
centers = [(ll*1/2, ll*np.sqrt(3)/2), (-ll*1/2, ll*np.sqrt(3)/2), (ll*1/2, -ll*np.sqrt(3)/2), (-ll*1/2, -ll*np.sqrt(3)/2), (ll,0), (-ll,0)]
U_total = generate_gaussian_sources(X0, Y0, centers, w)
U_total2 = generate_gaussian_sources(X0, Y0, centers, w)
# 透镜调制
U_after_lens = apply_lens_phase_factor(U_total, X0, Y0, f, lambda_)
# 利用矩阵乘法计算出射面光场复振幅
start_time = time.time()
u1 = matrix_method(U_after_lens, k, d, x, y, x0, y0)
checkpoint_time = time.time()
T['matrix_method'] = checkpoint_time-start_time
I1 = np.abs(u1)**2
I1 = I1 / I1.max()
# 绘制
plt.figure()
plt.imshow(I1)
plt.title('matrix_method')
plt.colorbar()
# 利用积分法计算出射面光场复振幅
#u2 = integrate_method(U_after_lens, d, lambda_, X0, Y0, X, Y)
#I2 = np.abs(u2)**2
#I2 = I2 / I2.max()
# 绘制
#plt.figure()
#plt.imshow(I2)
#plt.title('integrate_method')
#plt.colorbar()
# 两次傅里叶方法
start_time = time.time()
u5 = d_fft_method(U_after_lens, d, lambda_, dx0, dy0)
checkpoint_time = time.time()
T['d_fft_method'] = checkpoint_time-start_time
I5 = np.abs(u5)**2
I5 = I5 / I5.max()
# 绘制
plt.figure()
plt.imshow(I5)
plt.title('d_fft_method')
plt.colorbar()
# 三次傅里叶方法
start_time = time.time()
u3 = t_fft_method(U_after_lens, d, lambda_, dx0, dy0, L0)
checkpoint_time = time.time()
T['t_fft_method'] = checkpoint_time-start_time
I3 = np.abs(u3)**2
I3 = I3 / I3.max()
# 绘制
plt.figure()
plt.imshow(I3)
plt.title('t_fft_method')
plt.colorbar()
# 单次傅里叶
start_time = time.time()
u4 = s_fft_method(U_after_lens, d, lambda_, X0, Y0)
checkpoint_time = time.time()
T['s_fft_method'] = checkpoint_time-start_time
I4 = np.abs(u4)**2
I4 = I4 / I4.max()
# 绘制
plt.figure()
plt.imshow(I4)
plt.title('s_fft_method')
plt.colorbar()
# 光源绘制
plt.figure()
plt.title('origin_img')
plt.imshow(np.abs(U_total))
plt.colorbar()
plt.show()
print(T)代码中调用的方法
import numpy as np
from tqdm import tqdm
from scipy.fftpack import *
def generate_gaussian_sources(xx, yy, centers, sigma_x=1, sigma_y=None):
if sigma_y is None:
sigma_y = sigma_x
# 初始化叠加后的高斯光源矩阵
gaussian_sources = np.zeros(xx.shape)
# 计算每个高斯分布并叠加
for center in centers:
center_x, center_y = center
# 高斯分布
exponent = - ((xx - center_x) ** 2 / sigma_x ** 2 + (yy - center_y) ** 2 / sigma_y ** 2)
gaussian_source = np.exp(exponent)
# 叠加到总光源矩阵
gaussian_sources += gaussian_source
return gaussian_sources
def apply_lens_phase_factor(U, X, Y, f, lambda_):
k = 2 * np.pi / lambda_
phase_factor = np.exp(-1j * k * (X**2 + Y**2) / (2 * f))
return U * phase_factor
def matrix_method(U, k, d, x, y, x0, y0):
X0, Y0 = np.meshgrid(x0, y0)
# 构建矩阵Mx, My和M
Mx = np.exp(-1j * k / d * np.outer(x, x0))
My = np.exp(-1j * k / d * np.outer(y0, y))
M = U * np.exp(1j * k * (X0 ** 2 + Y0 ** 2) / (2 * d))
# 利用矩阵乘法计算出射面光场复振幅
return Mx @ M @ My
def d_fft_method(U, d, lambda_, dx, dy):
k = 2 * np.pi / lambda_
# 轴向传播在频率域的传递函数
fx = np.linspace(-1/(2*dx), 1/(2*dx), U.shape[0])
fy = np.linspace(-1/(2*dy), 1/(2*dy), U.shape[1])[::-1]
FX, FY = np.meshgrid(fx, fy)
t = 1j*k*d
uxs = np.sqrt(1 - (lambda_*FX)**2 - (lambda_*FY)**2)
H = np.exp(t * uxs)
# 将光场变换到频率空间
U1=fftshift(fft2(U))
U2=H*U1
u2=ifft2(ifftshift(U2))
return u2
def t_fft_method(U, d, lambda_, dx, dy, L):
k = 2 * np.pi / lambda_
# 轴向传播在频率域的传递函数
x = np.linspace(-L / 2, L / 2, U.shape[0])
y = np.linspace(-L / 2, L / 2, U.shape[1])
X, Y = np.meshgrid(x, y)
H = np.exp(1j * k / (2*d) * (X ** 2 + Y ** 2))
# 将光场变换到频率空间
H_freq = fft2(H)
U_freq = fft2(U)
# 应用传递函数
U_freq_after_TTF = U_freq * H_freq
# 将光场变换回实空间
U_z = np.exp(1j*k*d)/1j/lambda_/d * fftshift(ifft2(U_freq_after_TTF))
return U_z
def s_fft_method(U, d, lambda_, X, Y):
k = 2 * np.pi / lambda_
Lx = X.shape[0] * lambda_ * d / (X[-1,-1]-X[-0, -0])
Ly = Y.shape[0] * lambda_ * d / (Y[-1,-1]-Y[-0, -0])
x1 = np.linspace(-Lx / 2, Lx / 2, X.shape[0])
y1 = np.linspace(-Ly / 2, Ly / 2, Y.shape[0])
X1, Y1 = np.meshgrid(x1, y1)
F0 = np.exp(1j * k * d) / (1j * lambda_ * d) * np.exp(1j * k / 2 / d * (X1 ** 2 + Y1 ** 2))
F = np.exp(1j * k / 2 / d * (X ** 2 + Y ** 2))
F = fftshift(fft2(U*F))
return F0 * F
return U
def integrate_method(U, d, lambda_, Xin, Yin, Xout, Yout):
dx = Xin[1] - Xin[0]
dy = dx
# 计算波矢
k = 2 * np.pi / lambda_
phase_shift = k / (2 * d)
# 初始化传播后的场分布
u_propagated = np.zeros((Xout.shape[1], Yout.shape[0]), dtype=np.complex128)
# 对整个空间进行积分以计算传播后的场分布
for i in tqdm(range(Xout.shape[1]), desc="Outer Loop"):
for j in range(Xout.shape[0]):
-1j / lambda_ / d * np.exp(1j * k * d) * sum(sum(U * np.exp(1j * k / 2 / d * ((Xout[i, j] - Xin) ** 2 + (Yout[i, j] - Yin) ** 2))))
return u_propagated3.结果
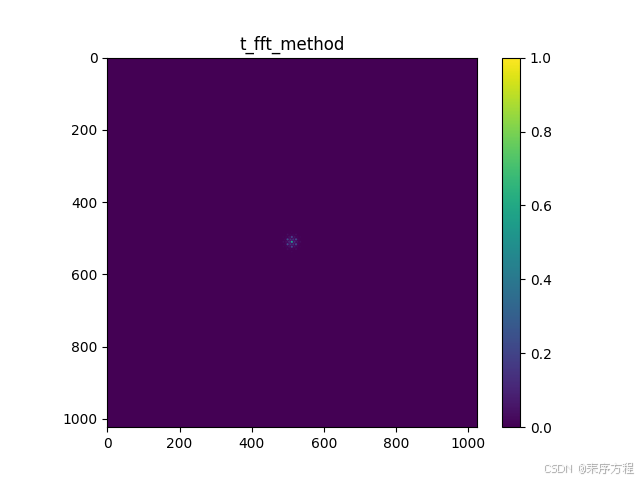
放出结果

这里读者如果理解了上面的思考问题,就可以理解这里的矩阵方法是可以通过调整计算范围来调整准确度的。



4.结论
| 方法 | matrix_method | t_fft_method | s_fft_method | d_fft_method |
| t/s | 0.106697 | 0.101677 | 0.069767 | 0.123922 |
5.参考
人类能看懂的衍射光学(含基尔霍夫衍射,瑞利--索末菲衍射,夫琅禾费衍射,角谱衍射,菲涅尔衍射积分,菲涅尔衍射的S-FFT算法,T-FFT算法,D-FFT算法)_瑞利索末菲衍射积分公式-CSDN博客
标量衍射计算指南(python 实现) - 楚千羽 - 博客园
一种快速实现光场传输的算法研究_龚海龙























 4389
4389

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








