上次介绍了冒泡排序,这次要说的是同属于交换排序中的另一种排序方法:快速排序。
快速排序是由冒泡排序改进而得的,它是一种有效的排序算法,虽然算法在最坏的情况下运行时间为O(n^2),但
由于平均运行时间为O(nlogn),并且在内存使用、程序实现复杂性上表现优秀,尤其是对快速排序算法进行随机化的
可能,使得快速排序在一般情况下是最实用的排序方法之一。快速排序被认为是当前最优秀的内部排序方法。由于快
速排序使用了分治的基本思想,所以很多公司面试都喜欢考这个,包括软考,考研等。
通过阅读很多人的关于快速排序的博客,再加上自己的理解和亲自实验,更深入的领会了分治法的思想。
首先介绍一下快速排序的基本思想:
1、在带排序的记录中任意取一个记录(通常取第一个)将它作为枢轴,设为X。附设指针i和j,分别指向表的上界和下界;
2、第一次交换,当i<j时,从右向左找到比X小的记录,并和X的值进行交换;
3、第二次交换,当i<j时,从左向右找到比X大或者等于的记录,并和X的值进行交换;
4、重复2、3步骤,直到i=j时终止,此时i或j的位置即为枢轴在此趟排序中的最终位置,原表被分成左右两个表。
具体代码如下:
/*********快速排序*********/
#include<stdio.h>
void quick_sort(int array[], int L, int R);
void main()
{
int array[10] = {49,38,65,97,76,13,25,27,86,49};//随意列举10个数
quick_sort(array, 0, 9);
for (int i = 0 ; i<=9 ; i++) //输出10个数
{
printf("%d ",array[i]);
}
printf("\n");
}
//定义递归函数
void quick_sort(int array[], int L, int R)
{
if(L < R)
{
int i = L,j = R; //将L(最左侧数的下标)和R的(最右侧数的下标)分别赋值给i,j
int x = array[L]; //设置一个枢轴x,取最左侧的数
while(i < j)
{
while(i < j && array[j] >= x) //第一次从右往左找到比x小的数,并将其赋值给array[i]
j--;
array[i] = array[j];
while(i < j && array[i] < x) //第二次从左往右找到比x大或等于的数,并将其赋值给array[j]
i++;
array[j] = array[i];
}
array[i] = x; //一趟排序的后,此时i=j,再将x的值赋给array[i]或array[j]
//递归调用
quick_sort(array, L, i-1); //将i左边的数再次调用该函数
quick_sort(array, i+1, R); //将i右边的数再次调用该函数
}
}接下来我们以49,38,65,97,76,13,25,27,86,49随机取的10个数进行一下分析:
1、首先第一步是找到一个枢轴,这里以取第一个为例,即取x=array[ i ]=49(x先保存下第一个数的值):
2、代码函数中的第一次循环,从右到左找到一个比49小的数array[ j ],即图中的27:
while(i < j && array[j] >= x)
j--;
array[i] = array[j];
然后将该值赋值给array[ i ],此时27的位置也就空了出来,
3、代码函数中的第二次循环,从左到右找到一个比49大的数array[ i ],即图中的38:
while(i < j && array[i] < x)
<span style="white-space:pre"> </span>i++;
array[j] = array[i];
然后将该值赋值给array[ j ],此时原来的38的位置便空了出来,
4、在最外层循环体的条件下,重复执行以上2和3,最后经过一趟排序完成后,此时下标 i=j ,如图:
最后再把最开始记录下的x的值49赋值给array[ i ],即array[ i ]=x,
经过这一趟排序后,产生了以49为枢轴的左右两个字表,此时在进行最后的递归调用
quick_sort(array, L, i-1); //将i左边的数再次调用该函数
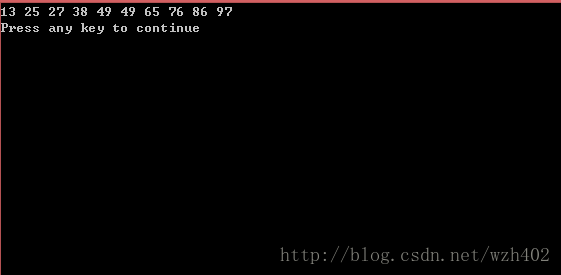
quick_sort(array, i+1, R); //将i右边的数再次调用该函数得出结果:
挖坑方法总结:
1.i =L; j = R; 将基准数挖出形成第一个坑array[ i ]。
2.j--由后向前找比它小的数,找到后挖出此数填前一个坑array[ i ]中。
3.i++由前向后找比它大的数,找到后也挖出此数填到前一个坑array[ j ]中。
4.再重复执行2,3二步,直到i=j,将基准数填入array[ i ]中。










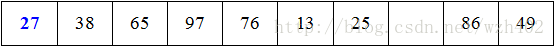
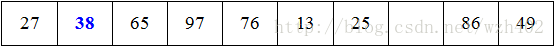




















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








