codeforces 30D King's Problem? 数学

题意:

给定一个坐标系。
有n个点在x轴上，一个点不在x轴上。
询问从给出的第k个点开始走遍所有的点的最小距离花费。
距离定义为两点的欧几里得距离。

---

解析:

首先考虑起始点是第n+1个点。
那么答案要么是这样

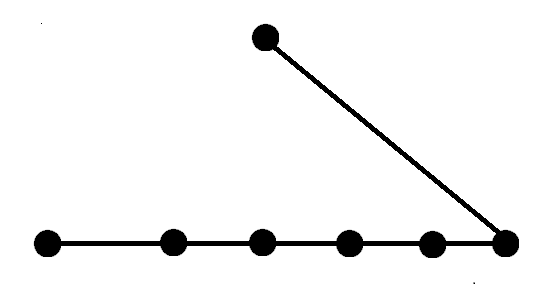
要么是这样

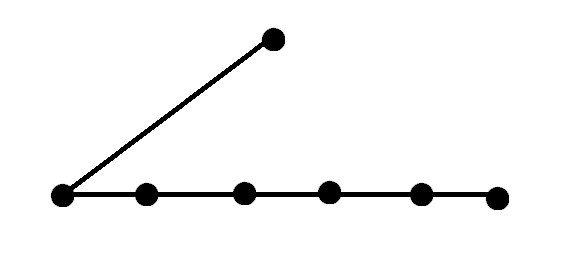
对于起始点不是第n+1个点的情况。
那么答案只有几种情况
为了方便说话我们把x轴的点的编号按照x坐标编号。
第一种情况：设起始点为p
那么从p->1->n+1->p+1->n
第二种情况：p->1->n+1->n->p+1
第三种情况：p->n->n+1->p-1->1
第四种情况：p->n->n+1->1->p-1
因为题中限制每个点可以走两次，所以有额外的情况
额外的情况：从点p可以先往右走一点，再向左一直到1，重复1,2情况。
或者从点p先向左走一点，再向右一直到n，重复3,4情况。
其实上述这么一大坨子讨论就是枚举一个从p可能再次走到的另一个点，看做从那个点走。
代码比较好实现。

---

代码:

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define N 100100
using namespace std;
int n,k;
double newtag;
double xx[N];
double ans;
double y;
double get_dis(int l)
{
    return sqrt((xx[l]-xx[n+1])*(xx[l]-xx[n+1])+y*y);
}
double dis[N];
double to[N];
double calc1(int l,int r)
{
    return xx[r]-xx[l]+min(get_dis(l),get_dis(r));
}
double calc2(int l,int r)
{
    return xx[r]-xx[l]+min(get_dis(l)+fabs(newtag-xx[r]),get_dis(r)+fabs(newtag-xx[l]));
}
int main()
{
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n+1;i++)
    {
        int x;
        scanf("%lf",&xx[i]);
    }
    scanf("%lf",&y);
    newtag=xx[k];
    sort(xx+1,xx+n+1);
    if(k==n+1)
    {
        double ans=calc1(1,n);
        printf("%.10lf\n",ans);
    }else
    {
        double ans=calc2(1,n);
        for(int i=1;i<n;i++)
        {
            ans=min(ans,min(calc1(1,i)+calc2(i+1,n),calc2(1,i)+calc1(i+1,n)));
        }
        printf("%.10lf\n",ans);
    }
}