ADPCM算法浅析

ADPCM算法浅析

1. ADPCM算法简介

1.1 脉冲编码调制（PCM）的概念

• PCM是pulse code modulation的缩写
• 概念上最简单、理论上最完善、最早研制成功、使用最为广泛、数据量最大的编码系统
  

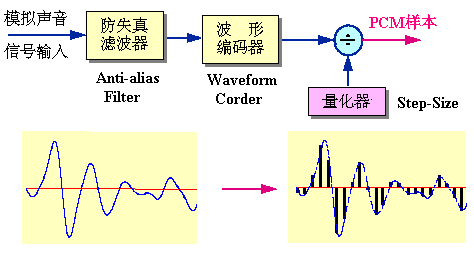
在上图中：

• 输入是模拟信号，输出是PCM样本。
• 防失真滤波器：低通滤波器，用来滤除声音频带以外的信号
• 波形编码器：可理解为采样器
• 量化器：可理解为“量化阶大小(step-size)”生成器或者称为“量化间隔”生成器

PCM实际上是模拟信号数字化：

• 第一步是采样，就是每隔一段时间间隔读一次声音的幅度
• 第二步是量化，就是把采样得到的声音信号幅度转换成数字值

1.2 量化的方法

量化的方法主要有均匀量化和非均匀量化。

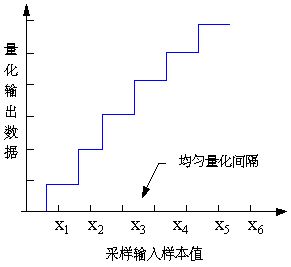
均匀量化：
- 采用相等的量化间隔/等分尺度量采样得到的信号幅度，也称为线性量化。
- 量化后的样本值Y和原始值X的差E=Y-X称为量化误差或量化噪声

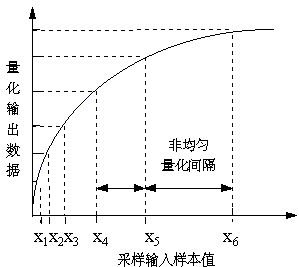
非均匀量化

• 大的输入信号采用大的量化间隔，小的输入信号采用小的量化间隔
• 可在满足精度要求的情况下用较少的位数来表示
• 声音数据还原时，采用相同的规则
• 采样输入信号幅度和量化输出数据之间定义了两种对应关系（μ律压扩算法，A律压扩算法）注：压扩(companding)
  

μ律压扩

• μ律(μ -Law)压扩(G.711)主要用在北美和日本等地区的数字电话通信中，按下式确定量化输入和输出的关系：
  x为输入信号幅度，规格化成 sgn(x)为x的极性；
• u为确定压缩量的参数，它反映最大量化间隔和最小量化间隔之比，取100≤u≤500。
• 由于u律压扩的输入和输出关系是对数关系，所以这种编码又称为对数PCM。具体计算时，用u＝255，把对数曲线变成8条折线以简化计算过程。

A律压扩

• A律(A-Law)压扩(G.711)主要用在欧洲和中国大陆等地区的数字电话通信中，按下式确定量化输入和输出的关系：
  0≤ |x|≤1/A
  1/A < |x|≤1
• x为输入信号幅度，规格化成 -1≤x≤1; sgn(x)为x的极性。
• A为确定压缩量的参数，它反映最大量化间隔和最小量化间隔之比。

小结：PCM编码早期主要用于话音通信中的多路复用。一般来说，在电信网中传输媒体线路费用约占总成本的65%，设备费用约占成本的35%，因此提高线路利用率是一个重要课题。

1.3 自适应差分脉冲编码调制（ADPCM）的概念

• ADPCM的中文术语为自适应差分脉冲编码调制
• adaptive difference pulse code modulation的缩写
• 综合了APCM的自适应特性和DPCM系统的差分特性，是一种性能比较好的波形编码技术

它的核心想法是：

• 利用自适应的思想改变量化阶的大小，即使用小的量化阶(step-size)去编码小的差值，使用大的量化阶去编码大的差值。
• 使用过去的样本值估算下一个输入样本的预测值，使实际样本值和预测值之间的差值总是最小

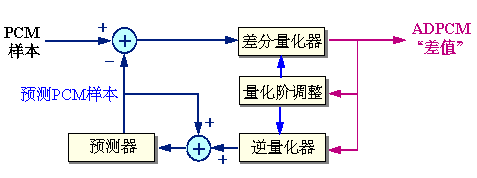
1.4 ADPCM编码框图

接收端的译码器使用与发送端相同的算法，利用传送来的信号来确定量化器和逆量化器中的量化阶大小，并且用它来预测下一个接收信号的预测值。

2 ADPCM代码实现

2.1 ADPCM编码程序逻辑

由待编码文件的起始部分开始，依次读取长度为len的数据段，送入adpcm_encoder，得到编码后的数据，并将结果存入中间文件，直到待编码文件的所有部分都已编码完成。

adpcm_reset(); //此函数只需在编码开始前调用一次

while(待编码文件未读完)
{
    读取长度为len的数据段,存入固定的数组内；
    执行adpcm_encoder，得到编码后的数据段，以及编码后的数据段长度len_2；
    将编码后的数据段顺次存入中间文件内；
}

2.2 ADPCM解码程序逻辑

由中间文件的起始部分开始，依次读取长度为len_2的数据段，送入adpcm_decoder，得到编码后的数据，并将结果存入最终文件，直到中间文件的所有部分都已解码完成。

while(中间文件未读完)
{
    读取长度为len_2的数据段,存入固定的数组内；
    执行adpcm_decoder，得到解码后的数据段；
    将解码后的数据段顺次存入最终文件内；  
}

2.3 代码示例

//#include <stdafx.h>
#include "ADPCM_thirdparty.h"   

static short s_valprev;
static char s_index;

/* Intel ADPCM step variation table */   
static int indexTable[16] = {   
    -1, -1, -1, -1, 2, 4, 6, 8,   
    -1, -1, -1, -1, 2, 4, 6, 8,   
};   

static unsigned int stepsizeTable[89] = {   
    7, 8,