多校联考 Day 3 / 4 题解
多校联考 Day 3
T1

\qquad 本题最先映入眼帘的显然是那 a i a_i ai 范围的限制: a i ≤ 2 64 a_i \leq 2^{64} ai≤264,非常的恶心。不仅爆 l o n g l o n g long\;long longlong,还恰好比 u n s i g n e d l o n g l o n g unsigned\;long\;long unsignedlonglong 大 1 1 1……这不纯属搞心态?但是读完题目我们发现,本题所需要的信息与 a i a_i ai 本身无关,只与 a i a_i ai 所有数位上包含多少个不同的数有关,所以我们果断选择用 c h a r char char 数组读入,然后用 b i t s e t bitset bitset 存一手信息。
\qquad 解决了这个恶心的数据范围,我们就开始分析题目。首先,这题也是一眼 d p dp dp, O ( n 2 k ) O(n^2k) O(n2k) 的暴力 d p dp dp 思路非常好想: d p i , j dp_{i,j} dpi,j 表示考虑到第 i i i 个数,划分了 j j j 段,最大代价是多少。转移式也是十分好写: d p i , j = max d p k , l − 1 + c o s t k + 1 , i dp_{i,j}=\max {dp_{k,l-1}+cost_{k+1,i}} dpi,j=maxdpk,l−1+costk+1,i, c o s t k + 1 , i cost_{k+1,i} costk+1,i 代表从 k + 1 k+1 k+1 到 i i i 分为一段,花费为多少,是可以 O ( n 2 ) O(n^2) O(n2) 预处理出来的。
\qquad
非常玄学的是,我写的
O
(
n
2
k
)
O(n^2k)
O(n2k) 的暴力竟然
A
A
A 了!!!

\qquad
时限四秒,但最慢的一个点只跑了三秒,跑的非常快……这是一个三方暴力该有的分数吗???
\qquad
我们回到上面的
d
p
dp
dp 转移式:
d
p
i
,
j
=
max
d
p
k
,
l
−
1
+
c
o
s
t
k
+
1
,
i
dp_{i,j}=\max {dp_{k,l-1}+cost_{k+1,i}}
dpi,j=maxdpk,l−1+costk+1,i,我们不难发现,
c
o
s
t
k
+
1
,
i
cost_{k+1,i}
costk+1,i 的值很小,只可能是
1
∼
10
1\sim 10
1∼10。对于若干
c
o
s
t
k
+
1
,
i
cost_{k+1,i}
costk+1,i 相同的
k
k
k,我们只需找到这些
k
k
k 中,
d
p
k
,
l
−
1
dp_{k,l-1}
dpk,l−1 最大的即可。到了这一步,我们又发现,当
l
−
1
l-1
l−1 为定值时,
d
p
k
,
l
−
1
dp_{k,l-1}
dpk,l−1 一定是随着
k
k
k 的递增而递增的,因为分成的段数相同,数字越多代价一定不会减少,所以我们记
R
i
,
j
R_{i,j}
Ri,j 为:以
i
i
i 为右端点,花费为
j
j
j 的左端点的最大值。
![R[i][j]](https://img-blog.csdnimg.cn/66b63190605e4d3398c3a402e1129cc3.png)
\qquad
所以,我们的
d
p
dp
dp 转移式就可以成功优化为:
d
p
i
,
j
=
max
d
p
R
i
,
j
−
1
,
l
−
1
+
j
,
j
∈
[
1
,
10
]
dp_i,_j=\max {dp_{R_i,_j-1},_{l-1}+j},j\in [1,10]
dpi,j=maxdpRi,j−1,l−1+j,j∈[1,10]。然后它就会飞快地跑过本题。

\qquad
核心代码:
memset(dp, 0xcf, sizeof dp);
for(int i = 0; i <= n; i ++) dp[i][0] = 0;//注意这里!!!
/*
或许你以为,在这里我们只赋值dp[0][0]=0就够了,实则不然,这样只会获得30pts。反例如下:
1
100 2
11 11 1 1 1 10 13 23 17 1 1 17 16 1 19 19 5 13 1 1 19 21 19 21 1 29 19 10 16 16 7 1 1 13 7 1 26 15 7 10 1 13 16 15 25 7 1 27 11 1 19 23 25 28 1 1 25 1 27 25 25 1 19 1 1 4 11 25 1 26 1 1 9 23 21 25 13 1 25 25 3 7 1 25 1 28 9 21 1 21 25 6 14 16 14 1 27 16 11 1
这个数据前面几个数的代价都是1,所以他们的R[i][1]都是自己本身。那么很显然,dp[2][1]=dp[1][0]+1。答案显然应该是1,但是我们若只给dp[0][0]赋值为0,那么dp[2][1]的值就会和dp[1][0]一样成为负无穷,就只能喜提30pts了。
*/
for(int i = 1; i <= n; i ++)
for(int j = i; j >= 1; j --)
R[i][cost[j][i]] = max(R[i][cost[j][i]], j);
for(int i = 1; i <= n; i ++)
for(int l = 1; l <= min(i, k); l ++)
for(int j = 1; j <= 10; j ++)
if(R[i][j]) dp[i][l] = max(dp[i][l], j + dp[R[i][j] - 1][l - 1]);
printf("%d\n", dp[n][k]);
T2

\qquad 像这种计数题就是一眼 d p dp dp。话不多说,我们直接考虑如何设计 d p dp dp 状态。因为题目中要求:每一个点的编号要大于他的孩子们的编号,有这个限制我们应该怎么想呢?是不是考虑将节点 i i i 插入到节点 i + 1 ∼ n i+1\sim n i+1∼n 的子树里呢?这样这个限制就完美解决了。而且题目中还有一个至关重要的要求:孩子之间是有序的,这说明我们可以将节点 i i i 插入到节点 i + 1 ∼ n i+1\sim n i+1∼n 的子树中的任意一个空位,无需考虑重复计算的情况。这样便可使得不重不漏。有了这个思路的引导,我们考虑设计状态: d p i , j dp_{i,j} dpi,j 表示考虑到点 i i i,总共还剩 j j j 个空位,方案数是多少。那么我们想:假设我想让当前点 i i i 剩余 p p p 个空位,那么 d p i , j dp_{i,j} dpi,j 是不是应该从 d p i + 1 , j + 1 − p dp_{i+1,j+1-p} dpi+1,j+1−p 转移来呢(消耗一个空位,增加 p p p 个空位)?所以 d p i , j = ∑ k = j + 1 − d i j + 1 d p i + 1 , k × k dp_{i,j}=\sum_{k=j+1-d_i}^{j+1}dp_{i+1,k}\times k dpi,j=∑k=j+1−dij+1dpi+1,k×k。乘一个 k k k 是因为节点 i i i 可以插入到上面 k k k 个空位中的任意一个。注意到 d p i + 1 , k × k dp_{i+1,k}\times k dpi+1,k×k 与我们当前枚举的 j j j 无关,所以可以使用前缀和优化。
\qquad 核心代码:
memset(sum, 0, sizeof sum), memset(dp, 0, sizeof dp);
dp[n + 1][1] = 1;//开始只有一个根的空位
for(int i = 1; i <= n + 1; i ++) sum[i] = (sum[i - 1] + (1LL * dp[n + 1][i] * i) % mod) % mod;
for(int i = n; i >= 1; i --) {
for(int j = 0; j <= n; j ++) dp[i][j] = (sum[j + 1] - sum[max(0, j - d[i])] + mod) % mod;
for(int j = 0; j <= n + 1; j ++) sum[j] = (sum[j - 1] + (1LL * dp[i][j] * j) % mod) % mod;
}
printf("%d\n", dp[1][0]);
多校联考 Day 4
T1

\qquad
本题乍一看,好恶心啊……这个
f
(
i
)
f(i)
f(i) 的形式感觉没见过啊……但是冷静分析后,我们可以发现一件事:

\qquad
我们即使把最前面的几个质数相乘,乘到
47
47
47 之后就已经到
6
×
1
0
17
6\times 10^{17}
6×1017,大于
1
0
16
10^{16}
1016 了,这意味着我们的
f
(
i
)
f(i)
f(i) 是不会很大的。所以我们可以直接枚举
f
(
i
)
f(i)
f(i),然后统计
f
(
i
)
f(i)
f(i) 在
1
∼
n
1\sim n
1∼n 中出现几次即可。
\qquad 思路一(题解思路):我们打表发现 f ( i ) f(i) f(i) 都是大于 1 1 1 的,因为 1 1 1 是任何数的因子;偶数的 f ( i ) f(i) f(i) 都是大于 2 2 2 的,因为 2 2 2 是任何偶数的因子; 6 6 6 的倍数的 f ( i ) f(i) f(i) 都是大于 3 3 3 的,因为 2 , 3 2,3 2,3 是任何 6 6 6 的倍数的因子……因此, f ( i ) > v f(i)>v f(i)>v 的 i i i 的个数是 n l c m ( 1 , 2 , … , v ) \frac{n}{lcm(1,2,\dots,v)} lcm(1,2,…,v)n,计算每个数的贡献即可。
\qquad 思路二(本人思路):考场上本人没想到如此简洁的思路,绕了一个大弯。首先,显而易见的是 i i i 的倍数一定每 i i i 个数出现一次,而且这对于任意一个等差数列都是成立的,所以我们直接枚举 f ( i ) f(i) f(i),计算完 f ( i ) f(i) f(i) 的出现次数后把这些 i i i 从 n n n 中剔除,这样就能保证正确性,不重复。但是,我们枚举的数,每一个都会成为 f ( i ) f(i) f(i) 吗?比如说,没有一个数的 f ( i ) f(i) f(i) 是 6 6 6,因为它是 2 , 3 2,3 2,3 的倍数,那么它就一定是 6 6 6 的倍数。所以我们枚举到一个 j j j 时,只需判断一下它的因子在前面枚举过的数中出现过没有即可。注意,假设 j = p c j=p^c j=pc,且 p p p 是质数,那么 j j j 在剩下的数中每 p p p 次出现一次,而不是每 j j j 次出现一次。
\qquad 核心代码:
//思路一
LL n = read(), lcm = 1LL;
LL ans = n % mod;
for(LL i = 1LL; lcm <= n; i ++) {
lcm = lcm / __gcd(i, lcm) * i;
ans = (ans + n / lcm) % mod;
}
cout << ans << '\n';
//思路二
LL ans = 0;
for(LL i = 2LL; i <= 60LL; i ++) {
LL zi = check_li(i);//判断能否写成 p^c 的形式
if(!check_prime(i) && !zi) continue;
if(zi) {
LL k = zi;
LL rest = n / k;
LL cha = n - rest;
ans = (ans + (cha * i) % mod) % mod;
n = rest;
}
else {
LL rest = n / i;
LL cha = n - rest;
ans = (ans + (cha * i) % mod) % mod;
n = rest;
}
if(!n) break;
}
printf("%lld\n", ans % mod);
T2

\qquad
首先,本题一眼贪心直接贪心地取行、列最大值显然是错误的,反例如下:
2 6 10 1
1 1 1 1 1 1
1 1 1 1 1 1
\qquad 若我们直接贪心取行、列最大值,那么我们一定会直接取走两行,还剩 8 8 8 次,在拿完 6 6 6 次 0 0 0 后不得不拿两次负数。但是我们一开始若选择取 6 6 6 个列,然后再选择取 4 4 4 次 0 0 0,就可以避免取负数。那么应该怎么做呢?
\qquad 首先我们想,一个矩阵确定后,取它的最优策略就一定也定下来了,每个位置需要减几个 p p p 也是确定的了。那么我们是不是可以得到一个性质:对于最优策略的取法,打乱顺序不影响最终结果。所以我们基于上面的反例,可以想到:将行列拆开贪心,最后合并取最大值。这个思想和 [CSP-S 2021] 廊桥分配 的贪心思路非常相似。一个小细节就是在合并的时候记得减去行与列重复部分的 p p p 即可。
\qquad 核心代码:
for(int i = 1; i <= n; i ++) h.push(H[i]);
for(int i = 1; i <= m; i ++) w.push(W[i]);//用堆分别维护行、列最大值
for(int i = 1; i <= k; i ++) val_h[i] = val_h[i - 1] + h.top(), h.push(h.top() - m * p), h.pop();
for(int i = 1; i <= k; i ++) val_w[i] = val_w[i - 1] + w.top(), w.push(w.top() - n * p), w.pop();
LL ans = 0xcfcfcfcfcfcfcfcf;
for(int i = 0; i <= k; i ++) ans = max(ans, val_h[i] + val_w[k - i] - 1LL * i * (k - i) * p);
printf("%lld\n", ans);
T3
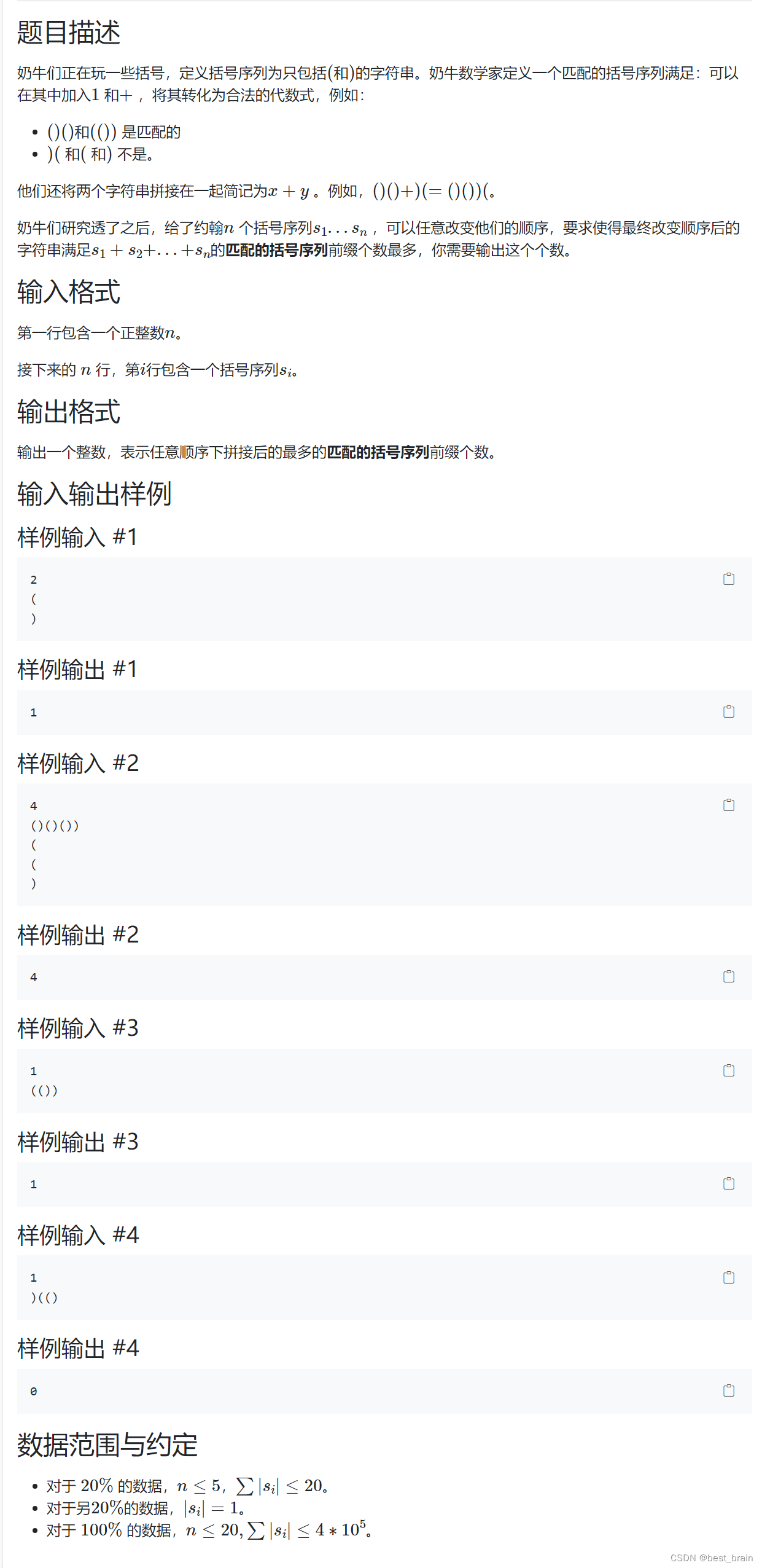
\qquad 首先,观察到本题的数据范围: n ≤ 20 n\leq 20 n≤20,显而易见的状压 d p dp dp。但是本题感觉状压 d p dp dp 的限制很多,因为括号序列还要考虑当前括号串是否合法(我们在此定义:不合法的串是有多余右括号的串,例如 ( ( ( ) ) ((()) ((()) 就是一个合法串, ( ( ) ) ) (())) (())) 就是一个不合法串),在此基础上还要统计拼接带来的代价,感觉十分繁琐。我们按顺序来考虑。
\qquad 一、如何判断当前穿添加上去后新串合不合法呢?这是括号匹配的一个经典套路:将左括号看成 1 1 1,右括号看成 − 1 -1 −1,若当前串存在一个前缀和小于 0 0 0 的前缀,那么他就是一个不合法的串。
\qquad 二、如何统计拼接带来的代价呢?首先我们假设将第 i i i 个括号串拼到长串 S S S 后面。那么长串 S S S 中多出的左括号显然可以和第 i i i 个括号串中多出的右括号匹配,产生代价。现在,我们想:假设长串 S S S 中多出的左括号数量为 c n t 1 cnt1 cnt1,第 i i i 个括号串中多出的右括号数量为 c n t 2 cnt2 cnt2,那么最终计算的时候使用 c n t 1 cnt1 cnt1 来算还是 c n t 2 cnt2 cnt2 来算,还是两者取 min \min min 呢?思考后发现应该用 c n t 1 cnt1 cnt1,因为我们求的是合法前缀数量,而不是合法的括号匹配对数。那也就意味着,若 c n t 1 > c n t 2 cnt1>cnt2 cnt1>cnt2,那么第 i i i 个括号串是不会产生任何代价的。有了以上两点,我们便可进行 d p dp dp 了。
\qquad 不过,还有一些必要的细节是需要注意的。例如,若 c n t 2 > c n t 1 cnt2>cnt1 cnt2>cnt1,那么第 i i i 个括号串拼到 S S S 后面之后产生的新串一定是不合法的。但是,这仍然是可以用来更新答案的。为了避免上面生成的不合法串继续更新后续导致错误,我们不妨钦定当前状态要保证合法,若不合法就不转移,只更新答案。
\qquad
核心代码:
for(int i = 1; i <= n; i ++) {
scanf("%s", s[i] + 1);
ls[i] = strlen(s[i] + 1);
int res = 0;
for(int j = 1; j <= ls[i]; j ++) {
res += (s[i][j] == '(' ? 1 : -1);
minn[i] = min(minn[i], res);
if(minn[i] == res) cnt[i][-res] ++;//若前面出现过比res小的,那么当前res状态与前面的串拼是一定不合法的
}
val[i] = res;
}
memset(f, 0xcf, sizeof f);
f[0] = 0;
int ans = 0;
for(int i = 0; i < (1 << n); i ++) {
for(int j = 1; j <= n; j ++) {
if((i >> (j - 1)) & 1) continue;
if(sum[i] + minn[j] >= 0) {//当前串与状态i的串拼起来是合法的,可以往后更新
f[i | (1 << (j - 1))] = max(f[i | (1 << (j - 1))], f[i] + cnt[j][sum[i]]);
sum[i | (1 << (j - 1))] = sum[i] + val[j];
}
else {//当前串与状态i的串拼起来后,后面就不允许再有别的串拼起来了,但是还是可以更新答案的
ans = max(ans, f[i] + cnt[j][sum[i]]);
sum[i | (1 << (j - 1))] = sum[i] + val[j];
}
}
ans = max(ans, f[i]);
}
T4
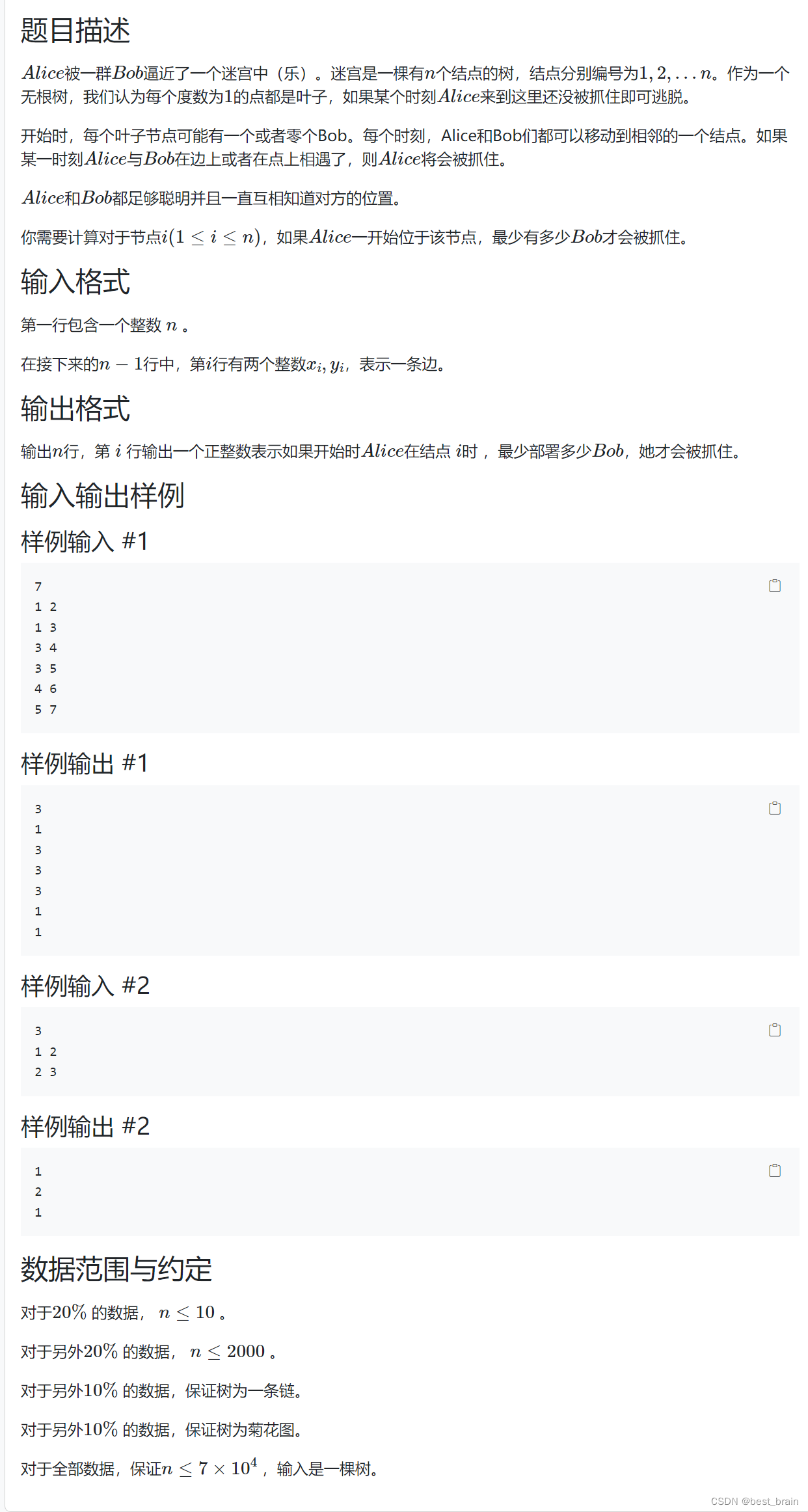
\qquad 首黑啊,Luogu P4183。
\qquad 首先,我们有一个暴力的思路:枚举以每个点 i i i 为根,然后遍历整棵树,对于每个点 j j j,记录一下 d i s i , j dis_{i,j} disi,j( i i i 到 j j j 的距离)和 g j g_j gj(距离 j j j 最近的叶子节点与 j j j 之间的距离)。那么若一个点 k k k 满足 g k ≤ d i s i , k g_k\leq dis_{i,k} gk≤disi,k,那么守住以点 k k k 为根的子树就仅需一个叶子,就是距离点 k k k 最近的那个叶子。然后统计一下最少需要几个类似的 k k k 才能包含住所有叶子即可。
\qquad 现在我们想,这个算法瓶颈在哪?显然是对于每个点 i i i 都把它当作根,每次都遍历整棵树这一步。显然,在这个过程中, g x g_x gx 是定值,可以预处理出来。那么我们只需考虑对于每一个 i i i,如何统计答案。
\qquad 回顾刚刚的思考过程,发现我们统计的是必要的 k k k,而这个 k k k 是一棵子树的根。不难发现,在这棵子树中的每一个点 q q q 都满足 g q ≤ d i s i , q g_q\leq dis_{i,q} gq≤disi,q,所以我们想要进行一步转化:把合法的子树 k k k 设置一个 1 1 1 的权值,然后统计权值和即可(这里的子树要求是极大的,意思是不能再向这棵子树中加点)。然而,统计子树仍然是难搞的。但是,统计点数是很好搞的,所以,我们想要将问题转化为:通过给点赋对应的权值,使得统计所有合法的点的权值和刚好等于最终答案。接下来,我们便需要一点点数学推导。
假设以 k k k 为根的子树中包含的点的集合为 E E E, d e g i deg_i degi 表示第 i i i 个点的度数,则
∑ u ∈ E d e g u = 2 × ( ∣ E ∣ − 1 ) + 1 = 2 × ∣ E ∣ − 1 \sum_{u\in E}deg_u=2\times (|E|-1)+1=2\times |E|-1 ∑u∈Edegu=2×(∣E∣−1)+1=2×∣E∣−1
2 × ∣ E ∣ − ∑ u ∈ E d e g u = 1 2\times |E|-\sum_{u\in E}deg_u=1 2×∣E∣−∑u∈Edegu=1
∑ u ∈ E 2 − ∑ u ∈ E d e g u = 1 \sum_{u\in E}2-\sum_{u\in E}deg_u=1 ∑u∈E2−∑u∈Edegu=1
∑ u ∈ E 2 − d e g u = 1 \sum_{u\in E}2-deg_u=1 ∑u∈E2−degu=1
\qquad 有了上面的推导,我们发现:若给每个点赋一个 2 − d e g u 2-deg_u 2−degu 的权值,那任何一个子树中的点权和都是 1 1 1。这意味着,我们只需将满足条件的点的点权和相加之后,得到的就是合法子树 k k k 的数量。形式化地说,对于一个点 i i i,我们求满足 g j ≤ d i s i , j g_j\leq dis_{i,j} gj≤disi,j 的 j j j 的点权和。注意到 d i s i , j dis_{i,j} disi,j 相当于树上 i , j i,j i,j 两点间路径长度,我们便可将其转化为统计路径类问题,考虑用点分治解决。
\qquad 假设当前树根为 t t t,那么我们要找的就是 g j ≤ d i s i , t + d i s t , j g_j\leq dis_{i,t}+dis_{t,j} gj≤disi,t+dist,j 的 j j j 的点权和,也就是 g j − d i s t , j ≤ d i s t , i g_j-dis_{t,j}\leq dis_{t,i} gj−dist,j≤dist,i 的 j j j 的点权和。我们用一个权值树状数组统计即可。注意到 g j − d i s t , j g_j-dis_{t,j} gj−dist,j 可能小于 0 0 0,考虑整体加个偏移量即可。
C o d e : \qquad Code: Code:
#include <bits/stdc++.h>
using namespace std;
const int maxn = 7e4 + 10;
int n, root, maxx, all;
vector < int > son[maxn];
int du[maxn], g[maxn];//g[i]:点i与最近的叶子节点之间的距离(允许越过根)
struct Tree_array {
int c[maxn << 1];
inline int lowbit(int x) {return x & (-x);}
void add(int x, int y) {while(x <= (n << 1)) c[x] += y, x += lowbit(x);}
int ask(int x) {
int res = 0;
while(x) res += c[x], x -= lowbit(x);
return res;
}
}T;
int sze[maxn], d[maxn], ans[maxn];
bool vis[maxn];
void dfs1(int x, int fa) {//与子树内的叶子连
if(du[x] == 1) g[x] = 0;
for(auto v : son[x]) {
if(v == fa) continue;
dfs1(v, x);
g[x] = min(g[x], g[v] + 1);
}
}
void dfs2(int x, int fa) {//与子树外的叶子连
for(auto v : son[x]) {
if(v == fa) continue;
g[v] = min(g[v], g[x] + 1);
dfs2(v, x);
}
}
void get_root(int x, int fa) {
int cnt = 0; sze[x] = 1;
for(auto v : son[x]) {
if(vis[v] || v == fa) continue;
get_root(v, x);
sze[x] += sze[v], cnt = max(cnt, sze[v]);
}
cnt = max(cnt, all - sze[x]);
if(cnt < maxx) maxx = cnt, root = x;
}
void get_dis(int x, int fa) {
ans[x] += T.ask(d[x] + n);
for(auto v : son[x]) {
if(vis[v] || v == fa) continue;
d[v] = d[x] + 1;
get_dis(v, x);
}
}
void calc(int x, int fa, int opt) {
T.add(g[x] - d[x] + n, opt * (2 - du[x]));
for(auto v : son[x]) {
if(vis[v] || v == fa) continue;
calc(v, x, opt);
}
}
void solve(int x) {
vis[x] = 1;
T.add(g[x] + n, 2 - du[x]);//提前加入根的贡献
for(auto v : son[x]) {
if(vis[v]) continue;
d[v] = 1, get_dis(v, x), calc(v, x, 1);
}
for(auto v : son[x]) if(!vis[v]) calc(v, x, -1);
T.add(g[x] + n, du[x] - 2);//因为要做两遍,但是根只能供献一次,所以做完一遍就要清空
reverse(son[x].begin(), son[x].end());
for(auto v : son[x]) if(!vis[v]) get_dis(v, x), calc(v, x, 1);
ans[x] += T.ask(n);//统计子树内对根的贡献
for(auto v : son[x]) if(!vis[v]) calc(v, x, -1);
reverse(son[x].begin(), son[x].end());
for(auto v : son[x]) {
if(vis[v]) continue;
root = 0, all = sze[x], maxx = n;
get_root(v, 0), get_root(root, 0);
solve(root);
}
}
int main() {
scanf("%d", &n);
for(int i = 1, x, y; i < n; i ++) {
scanf("%d%d", &x, &y);
son[x].push_back(y), son[y].push_back(x);
du[x] ++, du[y] ++;
}
memset(g, 0x3f, sizeof g);
dfs1(1, 0), dfs2(1, 0);
maxx = n, root = 0, all = n;
get_root(1, 0), get_root(root, 0);
solve(root);
for(int i = 1; i <= n; i ++) printf("%d\n", (du[i] == 1 ? du[i] : ans[i]));
return 0;
}
























 439
439











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








