2023.10.19 33dai 全真模拟赛总计-CSDN博客

本文链接：https://blog.csdn.net/x052xiao/article/details/133935133

2023.10.19 33dai 全真模拟赛总结

总述
题目
- T1
- T2
- T3
- T4

总述

时间安排

$\qquad 8:00\sim 8:20$ 通读题面，大概每道题都在脑子里留了印象，思考了一下下（？）。今天的考试感觉很正规，这个感觉应该有一大部分来源于今天的 $p df$ 题面……然后就想着今天一定要打的保守一点，争取不挂分，算是 $CSP - S$ 前涨涨信心。然后开始想 $T 1$ 。

$\qquad 8:20\sim 9:20$ $T 1$ 很快有了一个思路，感觉挺正确的，理论时间复杂度 $O(n\,log\,n)$ ，就火速写了。写完之后测了一发样例发现错了，调试了一下发现假了……有点小崩，但是调整得很快，中间想了 $10 min$ 感觉无思路，就先写了 $n^2k$ 的暴力 $d p$ ，写完后很快想到了一个 $n\sqrt n$ 的，就写了，写完和 $n^2k$ 的拍上了。拍了一会挂了，一调发现 $n^2k$ 的是个假算法…… $1 h$ 内写出了两个假算法，只能苦笑了。

$\qquad 9:20\sim 10:40$ 开场读题的时候注意到了今天部分分很多，例如 $T 1$ 的 $n\sqrt n$ 能拿 $80 pt s$ ，实现好的话说不定还能多拿点（雾），就想着先放放，多拿点部分分应该也能排挺高的吧，就开 $T 2$ 了。 $T 2$ 想的非常顺，上来的思路就是正确的（指并查集维护），感觉可写，但是不会给一个并查集整体赋偏移量，就先放了，打算先打暴力。暴力真是一眼建图跑拓扑，火速写了，中间听 $klz\;dalao$ 说写了一种广为人知的算法被卡了，，，因为和自己的思路完全不同，所以对开始的并查集思路有点小怀疑，但是没管，继续写了拓扑。很快写完了，但是调了有一段。大概的历程：只写了拓扑——在拓扑的基础上加了并查集——入队时的条件加了一条当前点是并查集的根——发现拓扑是假的，换成了 $b f s$ ，然后过了样例。看到有 $10 pt s$ 的链，写了很长的线段树用来拿这 $10 pt s$ ，还好一遍过了，然后跟 $b f s$ 互拍上了。

$\qquad 10:40\sim 11:20$ 回想了一下 $T 1, T 2$ ，发现还是不会，感觉就差临门一脚，但就是想不到，就先写了 $T 3$ 的暴力。看到式子想着先推一推，简单推了一下发现 $O(n^3)$ 统计的式子可以轻易优化到 $O(n^2)$ ，发现可以直接过掉 $n\leq 10$ 的档，就写了。然后推了推菊花图，简单猜了个结论，写了之后拍了拍，感觉没问题就放了。

$\qquad 11:20\sim 11:40$ 看了眼 $T 4$ ，一点不会，直接跳。思考 $T 1, T 2$ 无果，直到比赛结束。

考试结果

$\qquad 90+70+50+0=210,Rank:+\infty$ ， $T 1$ 意外的多拿了 $10 pt s$ ，其他题也没挂分。发现大家 $T 2$ 过的比 $T 1$ 多，但是我 $T 1, T 2$ 都没过，感觉有点崩……快结束的时候想到了 $T 1$ 的枚举 $g c d$ ，思考怎么判断的时候只想到枚举因子，没想到枚举倍数了…… $T 1$ 听完枚举倍数就懂完了（不懂完也不行了）， $T 2$ 听到启发式合并就会了，发现考场上但凡 $T 2$ 往这边想到启发式合并，往那边想到带权并查集（虽然不太会），可能也能磕出来吧……

考试总结

$\qquad$ 部分分拿的差不多，但也就拿了点部分分……

$\qquad$ 怎么说呢，今天打的非常保守，开场前就打好了数据生成和对拍的模板，争取每道题都拍一拍，这也导致今天没挂分。但是还是有很多该拿的分没拿到、应该能想到的点没想到，比如 $T 1$ 的枚举倍数， $T 2$ 的暴力启发式合并， $T 4$ 的 $l e n = 1$ 的部分分。

$\qquad$ 现在没想到还是好事，权当积累经验了，CSP-S的赛场上一定要想到啊！！！

题目

T1

gcd
$\qquad$ 挺裸的题，枚举 $g c d$ 后判断它的倍数出现的次数是否大于等于 $k$ 次即可，复杂度是调和级数，约等于 $O(n\,log\,n)$ 。

T2

$\qquad$ 首先，本题的 $60 pt s$ 是很好拿的（？），每次建图之后暴力 $b f s$ 一遍即可。场上最开始写的拓扑，一顿乱改瞎改后就莫名改对了？很梦幻。大概的过程就是：钦定每个连通块的根的值为 $0$ ，然后模拟过程即可。

$\qquad$ 然后，很关键的一档分： $a_i+1=b_i$ ，这档性质分有着极强的引导性。 对于所有判定的点都挨着的情况，我们可以用并查集维护一段连通块，他们一定是连续的，并查集的时候顺便维护下当前连通块的左右端点，修改值的时候直接上线段树的区间修改即可。它有什么引导性呢？若不考虑连续，思考整个过程便是：用并查集维护每个连通块，合并的时候修改其中一个并查集内的值。场上只顾着想线段树了，忘了至关重要的一个“类暴力”解法：启发式合并！按照大小合并并查集，小的合到大的上，暴力修改小的并查集内的所有元素即可，用 $v ec t or$ 维护一下，整体时间复杂度可证明是 $O(n\,log\,n)$ 。

$\qquad$ 核心代码：

void merge(int x, int y, LL z) {
	int fx = Find(x), fy = Find(y);
	if(son[fx].size() > son[fy].size()) {
		LL cha = val[x] - z - val[y];
		for(auto p : son[fy]) val[p] += cha, son[fx].emplace_back(p);
		son[fy].clear(), bin[fy] = fx;
	}
	else {
		LL cha = val[y] - val[x] + z;
		for(auto p : son[fx]) val[p] += cha, son[fy].emplace_back(p);
		son[fx].clear(), bin[fx] = fy;
	}
}

T3

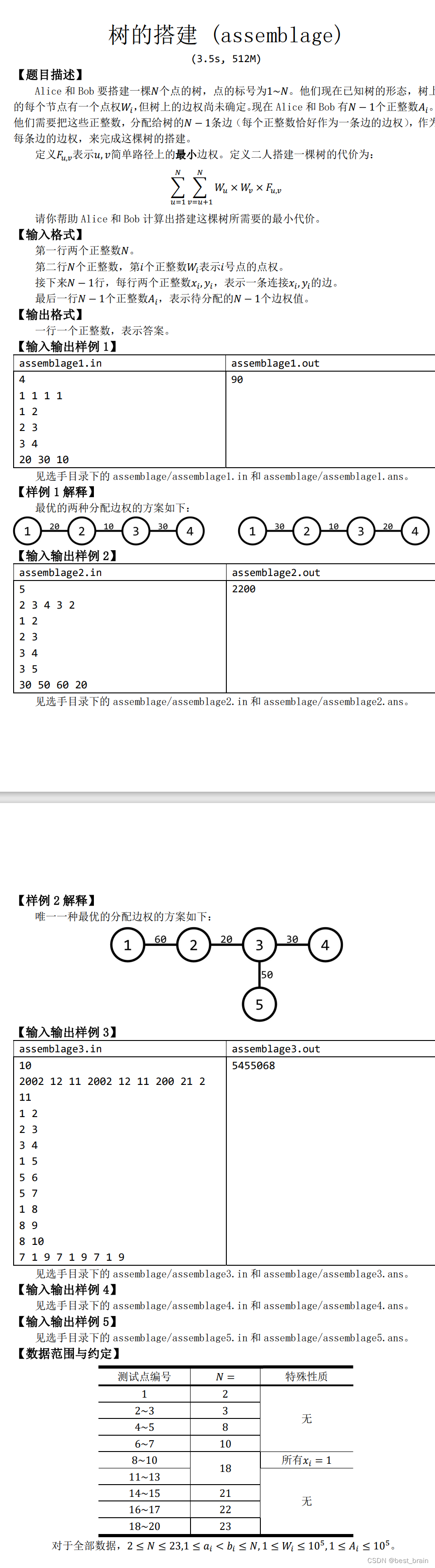
$\qquad$ 本题的部分分也是十分好拿。上面的式子把 $W_u$ 提到两个 $\sum$ 之间可以发现就是以每个点位根跑一遍树，边跑边记录边权最小值。然后直接 $df s$ 即可， $O(n^2n!)$ 轻松拿到 $35 pt s$ 。

$\qquad$ 对于菊花图，大胆猜测结论：把最大的边权赋给最小的点权，最小的边权赋给最大的边权。写完拍上就当证明了。

$\qquad$ 对于正解，数据范围告诉我们这题是个状压。但是压什么呢？~~上面的菊花图引导我们应该将边权排序~~我们先思考：若一开始便将整棵树（带边权、点权）给你，该如何在 $O(n\,log\,n)$ 的时间复杂度内计算这个式子呢？显然我们有两种做法：从小到大删边，从大到小加边。删边的过程感觉类似于点分治（好像是叫边分治？），因为一个较大的边能贡献到的点一定是要被较小的边给断开的。从大到小加边相当于一开始都是些散点，加一条边就是合并两个并查集，贡献就是两个并查集的 $W$ 和乘上边权。这引导我们应该将边权排序，按照上面的做法考虑填边。那么状压的状态也就呼之欲出： $ma s k$ 这个状态表示有哪些边已经填过了边权，有哪些边还没有填。假设 $ma s k$ 的二进制数中有 $k$ 个 $1$ ，那么我们接下来就应该用 $k + 1$ 大（小）的边权来填。计算的过程用上面两种实现方法均可，时间复杂度 $O(2^{n-1}\times n)$ 。

$\qquad$ 核心代码（从大到小加边）：

for(int i = 0; i < (1 << m) - 1; i ++) {
	int num = 1, Now = i;
	while(Now) num ++, Now -= (Now & (-Now));
	for(int j = 1; j <= n; j ++) bin[j] = j, sum[j] = w[j];
	for(int j = 1; j <= m; j ++) {
		if((i >> (j - 1)) & 1) merge(Edge[j].st, Edge[j].ed);//合并时顺便更新sum
	}
	for(int j = 1; j <= m; j ++) {
		if(!((i >> (j - 1)) & 1)) {
			dp[i | (1 << (j - 1))] = min(dp[i | (1 << (j - 1))], dp[i] + a[num] * sum[Find(Edge[j].st)] * sum[Find(Edge[j].ed)]);
		}
	}
}