吴恩达深度学习第一课第二周

第二周 神经网络基础

打卡（1）

2.1 二分类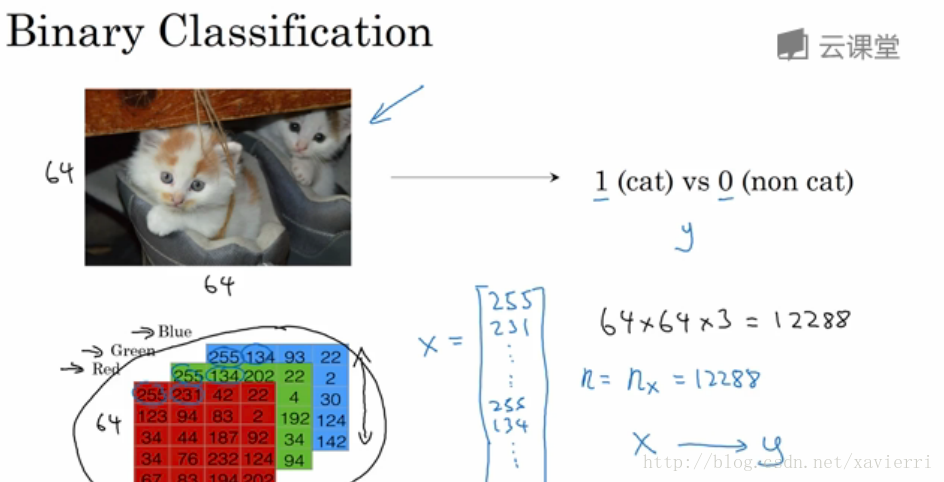

在二分分类问题中 目标是训练处一个分类器，它以图片（本例中）的特征向量X作为输入，来预测输出的结果标签y是1还是0，也就是预测图片中是否有猫。

课程中会用到的数学符号：

• $(x,y)$：表示一个单独的样本；
• $x\in R^{n_x}$:表示x是$n_x$维的特征向量；
• $y\in${0, 1} ：标签y值为0或1；
• 训练集有m个训练样本构成:$(x^{(1)},y^{(1)})$表示样本一的输入和输出；$(x^{(2)},y^{(2)})$表示样本二的输入和输出…$(x^{(m)},y^{(m)})$,这些样本整个一起就表示训练集，m表示训练样本的个数。 m=mtrain(训练