无向图的割点&&点双联通分量(Tarjan算法)总结

最新推荐文章于 2023-08-01 00:39:39 发布

AC-NEWBIE

最新推荐文章于 2023-08-01 00:39:39 发布

阅读量1.3k

点赞数 2

分类专栏：图论文章标签：图论点双联通 Tarjan算法

本文链接：https://blog.csdn.net/xbb224007/article/details/89403492

版权

图论专栏收录该内容

8 篇文章

订阅专栏

（一）预备知识：

无向图概念。
深度优先搜索、时间戳。

（二）概念介绍（建议参看其它文章QWQ）：

在一个无向图中，对于一个点对（u，v），如果从u至少有两条点不重复路径到达v，那么点u和点v在同一个点双联通分量中。而一个点双联通分量即为包含了尽可能多的这样的（u，v）点对的联通子图，且该子图中的任意两个点（u'，v'）均满足上述条件（除非这个双联通分量仅有这两个点--两个点也是双联通的）。
割点定义：在一个联通图中，若删除某个点可以使得该图不再联通，则该点为一个割点（故一个双联通分量中不存在割点）。一个割点可能属于多个不同的双联通分量，除割点外的外只会属于唯一的一个双联通分量。

（三）题解思路（可能有点乱~）：

（注：这里仅对Tarjan算法进行介绍，平时使用时基本也是用的该方法，并且只考虑图联通的情况(不连通可以分为多个不相干的联通图)）。

首先，我们从图的任意一个点开始进行dfs，可以得到一颗深度优先搜索树。我们将遍历至每个点时的深度优先数（时间戳）记录在一个数组pre[maxn]中（许多情况下写为dfn[maxn]）。
下图中pre[1]=1、pre[2]=2、pre[4]=3、pre[3]=4、pre[5]=5、pre[6]=6、pre[7]=7.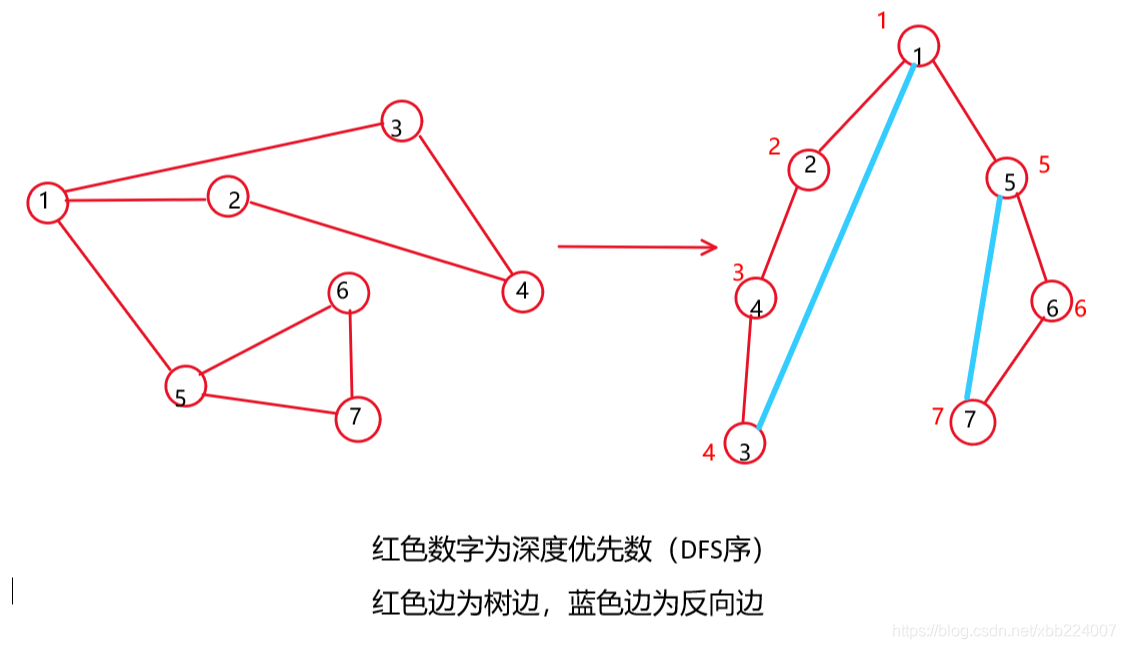
接下来我们考虑一下，这样生成的一棵树有什么性质(存在哪些种类的边)：
a、树边：从父节点指向子节点的边(上图中的红色大的边)；
b、反向边（回边）：从子节点指向祖先结点的边（不包括指向父节点的边，上图中蓝色的边）；
我们定义数组low[maxn]：low[u]为从u结点或u的子孙结点通过反向边可以达到的最低深度优先数。
low[u]可定义为：
low[u]=Min
{
pre[u],
Min{ low[v] | v是u的子节点},
Min{ pre[w] | w是u能通过反向边直接连回的祖先结点}
}
这个过程中low数组在dfs回退的过程中进行更新
上图中low数组的值分别为：low[3]=1、low[4]=1、low[2]=1、low[1]=1、low[5]=5、low[6]=5、low[7]=5;
我们先考虑割点怎么求，因为割点可以划分不同的双联通分量：
a、如果u不是树根：对于一个点u，其有一个子节点为v，如果low[v]>=pre[u]，说明结点u及其子孙结点均不能连回到u结点的祖先结点。那么当我们删除结点u（以及相关的边），结点v及其子孙结点将没有边和u以及u的祖先结点相连，即以v为根的子树会脱离出来，形成一个新的联通块，故u是一个割点。
b、如果u是树根：如果u的子节点数大于1，则u是割点。你可能会有疑问其不同的子节点间可能会有边相连？可以这么想，若果u的两个子树之间有边相连，那么在对其中一颗子树进行dfs时必然会搜索到另外一颗，即另外一颗子树不会是u的子树（也即无向图的深度优先搜索树中不会有“交叉边”）。
c、以上图而言，low[5]>=pre[5]、low[1]>=pre[1]，故1和5为割点。
接下来我们考虑如何求双联通分量：
a、通过上述介绍，我们可以在求low[]数组的时候进行割顶的判断，实际上我们也可以同时进行双联通分量的求解。
b、我们在进行深度优先搜索的过程中将经过的树边以及反向边压入一个栈进行保存，当我们求出来结点u是割点时，则使其为割点的子节点v及v的子孙结点便可以构成一个点双联通分量。此时我们将栈中存入的边出栈，直到遇到边（u，v）。
c、若上述v的子树中存在多个点双联通分量，则在回到v之前已经将相应的边出栈了，剩下的还是一个点双联通分量。
d、上图中有三个点双联通分量[1、2、3、4]、[5、6、7]，[1、5](计算时，包含结点5、6、7的边已经出栈)。
总的时间复杂度为线性的O(n+m)。
理解了求解过程以后（如果...），实现就是比较简单的过程了。

（四）代码模板（来自蓝书）：

#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<vector>
#include<stack>
#include<algorithm>
using namespace std;
const int maxn=1e4+10;
int bccno[maxn];//点所在的双联通分量编号--割点无意义
int iscut[maxn];//点是否是割点
int low[maxn];//low[u]表示点u及其后代能连回到的最早的祖先
int pre[maxn];//pre[u]表示点u第一次被访问到时的时间戳
int dfs_clk=0,bcc_cnt=0;
vector<int>G[maxn];
vector<int>bccp[maxn];
struct Edge{int u,v;Edge(int _u=0,int _v=0){u=_u;v=_v;}};
stack<Edge>S;
void Tarjan(int u,int f){
    low[u]=pre[u]=++dfs_clk;
    int sz=G[u].size();
    for(int i=0;i<G[u].size();i++){
        int v=G[u][i];
        if(!pre[v]){
            S.push(Edge(u,v));
            Tarjan(v,u);
            low[u]=min(low[u],low[v]);      //由其子孙结点更新
            if(low[v]>=pre[u]){             //此时u为割点
                ++bcc_cnt;
                for(;;){
                    Edge e=S.top();S.pop();
                    if(bccno[e.u]!=bcc_cnt)
                        bccno[e.u]=bcc_cnt,bccp[bcc_cnt].push_back(e.u);
                    if(bccno[e.v]!=bcc_cnt)
                        bccno[e.v]=bcc_cnt,bccp[bcc_cnt].push_back(e.v);
                    if(e.u==u&&e.v==v)break;//遇到边(u,v)时退出
                }
            }
        }
        else if(pre[v]<pre[u]&&v!=f)        //用反向边更新low[u]
            S.push(Edge(u,v)),low[u]=min(low[u],pre[v]);
        /*实际上也可以直接写为：
        else if(pre[v]<low[u]&&v!=f)
            S.push(Edge(u,v)),low[u]=pre[v];
        */
    }
}
int main(){
    #ifdef DanDan
    freopen("in.txt","r",stdin);
    #endif // DanDan
    int n,m,u,v;
    scanf("%d%d",&n,&m);
    for(int i=0;i<m;i++){
        scanf("%d%d",&u,&v);
        u--;v--;
        G[u].push_back(v);
        G[v].push_back(u);
    }
    for(int i=0;i<n;i++){
        if(!pre[i])
            Tarjan(i,-1);
    }
//    cout<<"cnt="<<bcc_cnt<<endl;         //输出测试
//    for(int i=1;i<=bcc_cnt;i++){
//        printf("i=%d: ",i);
//        for(int j=0;j<bccp[i].size();j++){
//            printf("%d ",bccp[i][j]);
//        }
//        printf("\n");
//    }
    return 0;
}