线代基础4

矩阵的转置：

矩阵A的行列式 = A转置矩阵的行列式

矩阵乘积的转置 与 矩阵转置的乘积 之间的关系：

推导出：
矩阵乘积的转置 = 矩阵转置的乘积(顺序相反)

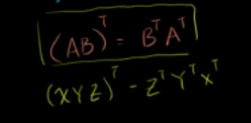
转置矩阵的加法与求逆运算

矩阵和的转置 = 矩阵转置的和

矩阵转置的逆 = 矩阵逆的转置

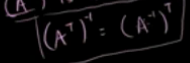
向量的转置：


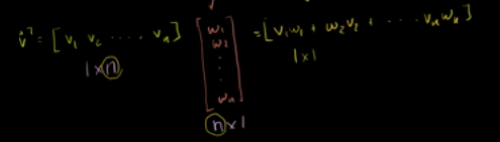
结论：两个向量的乘积(点乘) = 某个向量转置与另一个向量的乘积


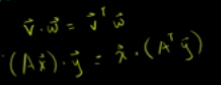
行空间和左零空间
零空间：
零空间就是行最简阶梯型的非主元的线性组合

列空间：
列空间就是主元的线性组合

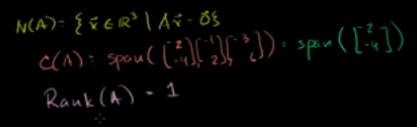
转置零空间(左零空间)：

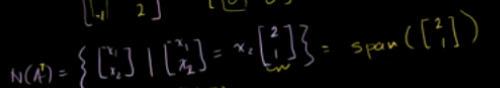
转置列空间(行空间)

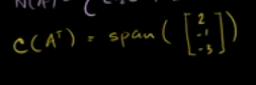
列空间 垂直 转置零空间(左零空间)
零空间 垂直 转置列空间(行空间)

矩阵的秩 = 矩阵列空间维度 = 转置矩阵的秩 = 矩阵行空间维度

正交补：
某个子空间v,它的正交补记作：

v的正交补是符合如上条件的x的集合。

Rn中，一个矩阵v的列空间的正交补就是v的左零空间。
v的秩(列空间纬度) = v转置的秩(v转置列空间纬度 或者 v行空间纬度)
v转置的秩 + v转置零空间(左零空间)纬度 = n
v的秩(列空间纬度) + 左零空间纬度 = n.

Rn中的一个子空间v的纬度 + v的正交补空间的纬度 = n
一个子空间v 与 v的正交补空间的交点 就是0向量。他们重合的元素只有0.
v的一组基 + v补的一组基 = Rn的一组基。
v属于Rn子空间，x属于Rn,则一定有v1,w1使得 x = v1(v1属于v) + w1(w1属于v补)

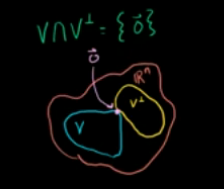
任何子空间的正交补的正交补就是原来的子空间。

(A转置)A是可逆:
如果A各列线性无关，则 (A转置)*A是方阵且可逆。证明略。

正交补与投影
向量x投影到子空间v，则x另一部分的投影在v补上。
可以做如下定义:
v属于Rn子空间，x属于Rn,则一定有v1,w1使得 x = v1(v1属于v) + w1(w1属于v补)

子空间投影是线性变换：
子空间v的一组基 b1,b2…bk;
定义矩阵A(b1,b2…bk)
那么，子空间里的任意一个向量 都可以用矩阵A(b1,b2…bk)点成向量y(矩阵A列向量如何组合)来表示。y未知。
可以取到合适的y来线性组合矩阵A的各个列向量来表示v上的任意一个向量。

向量x在子空间v中的投影 可以用矩阵A点成y的形式表达。这样就可以求出任何物体(由向量构成)投影到子空间(比如屏幕)后的表达形式。

由于向量x = x在v上的投影 + x在v补上的投影

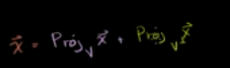
或者令w = x在v补上的投影，即：

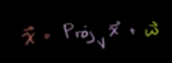
由于，子空间v相当于矩阵A的列空间，所以v补 = 矩阵A的左零空间(A转置的零空间)。
所以，A转置点成w(x在v补上的投影) = 0

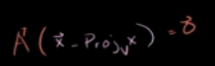
所以，x在v上投影用Ay表示后并展开得到：

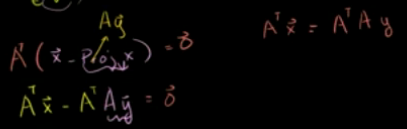
因为：如果A各列线性无关，则 (A转置)A是方阵且可逆
所以，A转置点乘A是可逆的，所以y有解。

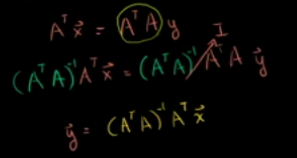
那么x在v上的投影就可以写成通式：

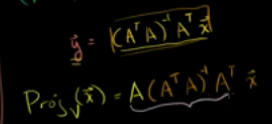
投影=矩阵点成向量的形式，也说明了投影是个线性变换。
也说明了 如果已知一个子空间的基向量，那么就可以构建一个矩阵A(由子空间基向量作为列向量)。通过这个矩阵可以求得任意向量在这个子空间的投影。也就是通过这个矩阵能够构建出投影变换矩阵。其形式就是：

例：
已知一个子空间v的一组基，求将向量x投影到这个子空间的变换矩阵。



所以，该变换矩阵就是一个1/3A(4*4),该矩阵是一个四乘四的方阵。

投影是子空间中距离原向量最近的向量
每个向量都可以理解为一个点，所以这里讨论的距离就是两点间的距离。

证明略

最小二乘：
如果矩阵Ax=b 无解，说明b不在A的列空间内。
那么A的列空间内存在一个距离b最近的向量，利用这个向量来估计b。
就是最小二乘估计 或 最小二乘逼近。

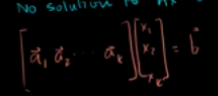
即在A列空间内寻找一个向量y,使得y与b最近。
显然，这个距离b最近的向量就是b在A的列空间的投影。
即用投影代替b，求出的解是最优解。

根据公式求投影有些麻烦，我们来寻找一个简单的最小二乘的求法：
两边同时减向量b：

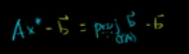
显然，投影向量减去b向量得到的是垂直于A列空间的向量。也就是A的列空间的正交补，也就是A的左零空间。

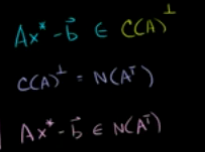
所以：

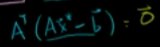
继续化简得到：

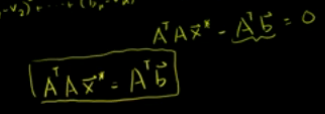
即：

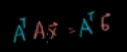
也就是当我们求Ax=b无解时，只要在两边同时乘以A的转置，就可以求出Ax=b的最优解。

最小二乘例题：
三条直线求交点

显然这三条直线没有相交于一点，所以方程组无解。
那么，利用最小二乘估计求出一个最接近的点 来近似估计这个交点。
即：

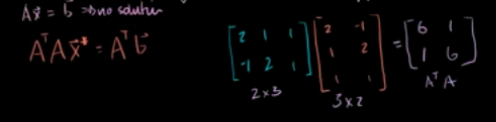
求出：

最小二乘例题：
已知4个点，求过这四个点的直线？

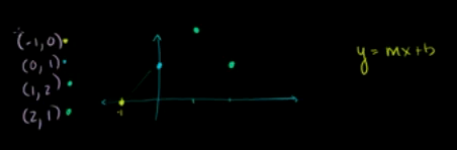
显然无法求出过四点的直线，则利用最小二乘估计 近似 求出距离四个点最近的一条直线。
首先设该直线为 y=mx+b,带入这四个点坐标，构建矩阵。

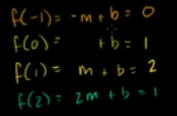
可见，该方程组无解。
构建矩阵：

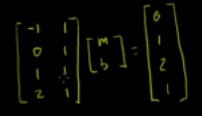
利用最小二乘 求出近似的 m,b

基变换：
已知向量b(3,-1),指的是在标准基下，


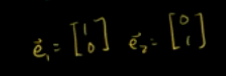
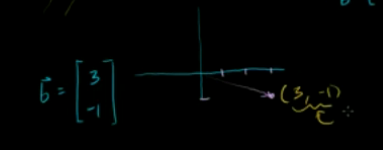
即：

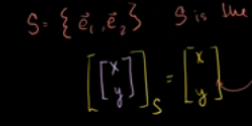
基底为v1,v2时 ，坐标变化图：

某基底B和标准基底下向量的转换：
C为B基底矩阵，a为标准基底下的向量
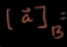为B基底下的向量

矩阵C把基底为B的向量改变到标准基底下，所以C就是基的变换矩阵。
已知基底B和基底B下的向量(7,-4)，求该向量的标准基坐标：
基底B下的坐标是2维，标准基下的是3维。因为基的变换矩阵列空间是在R3中的子空间。
子空间向量向R3空间转换

已知标准基底下的向量(8,-6,2),求该向量在基底B下的坐标：
利用增广矩阵消元，求出为(-3,11)
也就是R3空间向量向子空间转换

特殊情况：
如果基变换矩阵是可逆的，则:不需要建立增广矩阵消元解出基底B下的向量，用该基变换矩阵的逆乘以标准基向量就可以了

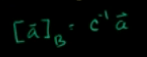
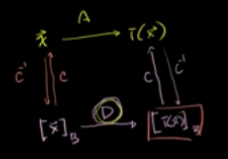
基底变换的情况：不同基底下的矩阵
向量在不同的基底下有不同的表达，矩阵在不同的基底下也有不同的表达。
同一个变换(变换效果相同)在不同基底下 表现为不同的矩阵。
A表示在标准基下的变换 ，D表示在B基底下的相同变换。
所谓相同变换是指：Ax=b , Dx(B)=b(B)即D乘以基底B下的x=基底B下的b

处理后得到：

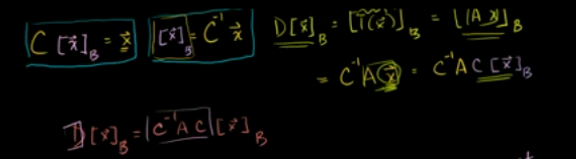
即:基底矩阵有逆矩阵

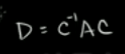
当B基底构成的基底矩阵为可逆时，标准基换成B基底后，变换矩阵A相应的变为基底矩阵C的逆乘以A再乘以基底矩阵C (C为B基底的基底矩阵)

继续推导：

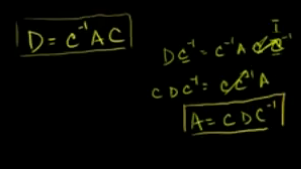
例子：


证明A和D是同一个变换，只是基底不同：

总结：
线性代数是一门选择合适基底的艺术
以下两个变换相同，基底不同，明显D变换使用的基底 能使运算更简单。

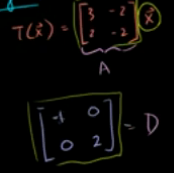
换基底求变换：
求x关于L对称的点的转换矩阵：

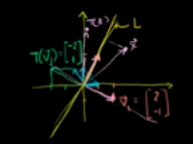
此变换关于L对称，如果L作为坐标轴来看的话，计算起来就会简单很多，所以把标准基换成v1(2,-1),v2(1,2)基底（下图基底B有误），在此基底下的变换为矩阵D，标准基下的变换为矩阵A。则

那么 v1在此基底B下的向量为：(1,0) v2在此基底下的向量为(0,1)
由此可见，在基底B下 矩阵D将v1,v2 变换到 -v1,v2.
由于v1,v2在基底B下坐标的特殊性，可以很容易求出矩阵D

求出D后 即可通过

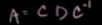
计算出标准基下的变换矩阵A。

标准正交基：
一组基 每个向量长度为1，且互相垂直。

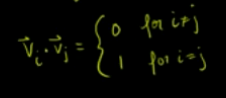
符合以上条件的向量集 必然线性无关，是一组基,证明略
标准正交基在运算中的特点：
x是标准基下的向量，属于子空间V
c(权重)是B基底下的向量坐标
v是B基底的基底元素

例：
B为标准正交基的子空间


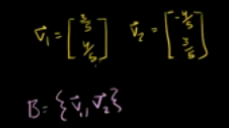
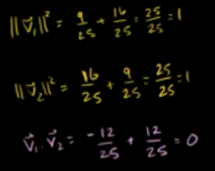
已知标准基下向量x（9，-2），求B基底下的x向量
B不是标准正交基的情况下：

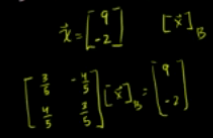
B是标准正交基的情况下：

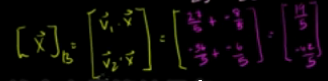
标准正交基下求投影的简化：
非标准正交基求投影：下图写法有误，第四项应该是A的转置

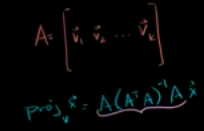
标准正交基求投影：
由于标准正交基的基变换矩阵有如下特点：

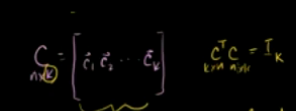
所以

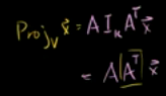
投影矩阵计算：

构造镜像变换：
已知v1,v2,v3 ,他们是一个正交集，是R3的一个正交基底。

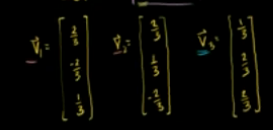
v1,v2张成一个平面子空间。v3垂直这个平面。
已知向量x属于R3，求x关于这个平面的镜像的变换矩阵。

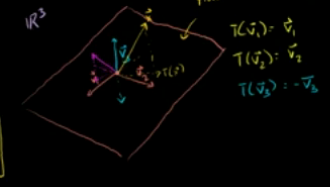
构建基底：
x属于R3，定义在标准基下，这时构建以v1,v2,v3为基底的坐标系，将使该变换更容易解决。
B{v1,v2,v3}基底构成的矩阵C为方阵，所以
C的转置=C的逆

所以在B基底下 v1,v2,v3的值为：

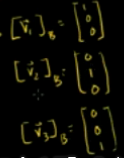
设新基底B下的变换矩阵D为：

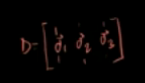
所以基底B下的这个变换可以表示为：

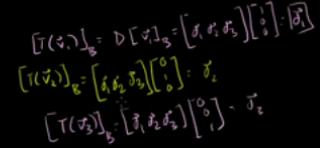
以为基底B下的该变换为：

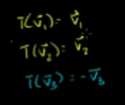
所以

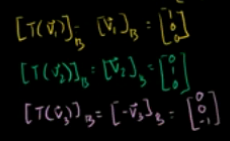
即基底B下的变换矩阵D为：

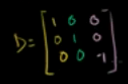
因为：

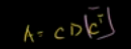
即：


正交的基底矩阵的保角性和保长性。C为正交基底矩阵(由标准正交基构成)

通过一组非标准正交基获得一组标准正交基的方法：
找到对应向量，出以该向量的模
互相垂直的向量通过投影的方法来找





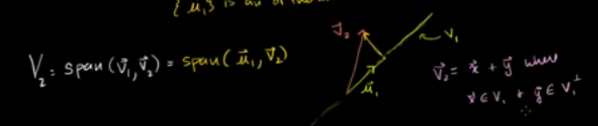
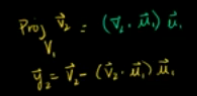
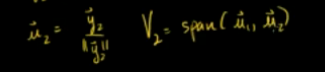
特征向量和特征值：
当我们在寻找一组基使变换的表达更加简单时，通常需要找到一组标准正交基，而这组基 通常能够使这个变换容易实现。
这组基在该变换下通常只是改变缩放比例或调转方向。
能够用如下表达：

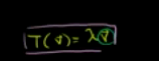
例如镜像变换

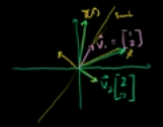
他的变换表达在换基之后为：

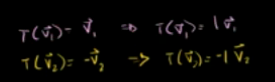
由于这些缩放比例对于定义基时很有用，因为在那些基下计算矩阵就变得简单了
所以 任何向量满足如下等式

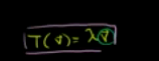
该向量叫做 特征向量，缩放比例叫做特征值。
所以特征向量通常是我们要寻找的基向量。

如下，v叫做矩阵A的特征向量

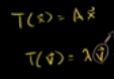
通过特征向量可以容易的找到该变换的一组基，使计算更容易。
很多变换寻找标准正交基并不把么容易，通过特征向量可以容易的确定一组基。

尝试寻找特征向量和特征值：
也就是寻找如下等式的解(零向量除外，因为零向量对构建一组基没有价值)




、
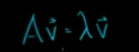
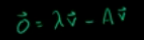
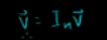
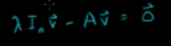
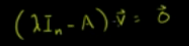相当于

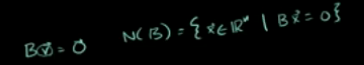
因为v不等于0，v在该矩阵的零空间，且假设该等式有解，说明该矩阵的列必然线性相关，零空间不是只包含0元素。
所以如下矩阵必然有线性相关的列，不可逆，行列式=0，零空间包含非平凡元素，零空间不仅仅包含零元素。

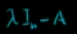
求解矩阵特征值：

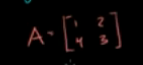
如下矩阵行列式=0




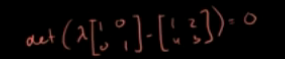
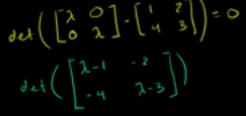
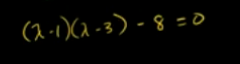
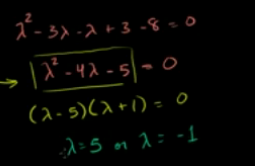
定义特征空间如下，特征向量构成的子空间。也就是如下矩阵的零空间

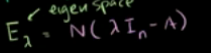
特征值=5时，特征空间就是如下矩阵的零空间

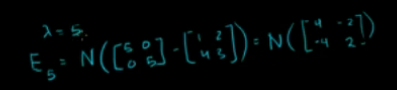
计算出这个矩阵的零空间为(1/2,1)

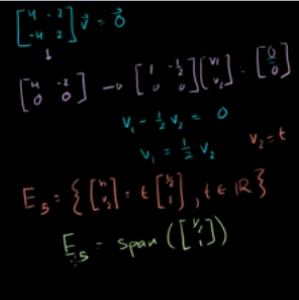
特征值=-1时，特征空间就是如下矩阵零空间，且求出零空间


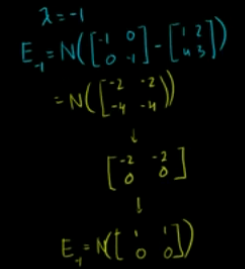
特征空间里的任意一个向量都是对应该特征值的有效特征向量

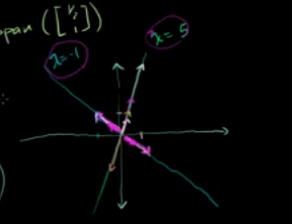
所以，矩阵A的特征值是-1和5，特征向量无限多个。特征向量张成的特征空间为如图的两条直线。

特征基有利于构造合适的坐标：
假设有变换如下

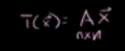
v1,v2…vn是矩阵A的特征向量，这些特征向量构成该空间的一组基，叫特征基。则

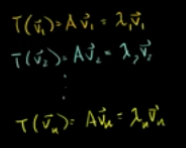
则



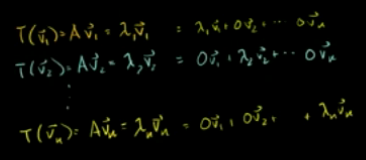
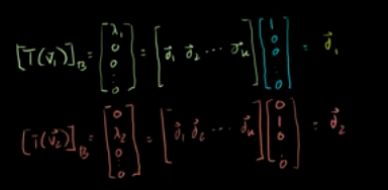
则