量子力学摘记2

5. 量子体系状态、算符与可观测量、表象

$\bullet$　量子体系状态
\qquad
\qquad 量子体系的状态用一个态矢量 $|\psi ⟩$ 描述，态矢量满足线性叠加性（即态叠加原理）：

$\begin{array}{rl}|\psi ⟩& =c_1|{\psi }_2⟩+c_2|{\psi }_2⟩\\ |\psi ⟩& =\sum _n{c}_n|{\psi }_n⟩\end{array}$
\qquad 右矢$\text{(ket)}$的厄密共轭$\text{(H.c.)}$定义为左矢$\text{(bra)}$，记为：$⟨\psi |=(|\psi ⟩{)}^{†}$，并有：
$(1)$ 态矢 $|\psi ⟩$ 和 $|\phi ⟩$ 的内积，记为：$⟨\psi \Vert \phi ⟩\equiv ⟨\psi |\phi ⟩$
$(2)$ 态矢 $|\psi ⟩$ 和 $|\phi ⟩$ 的正交性，记为：$⟨\psi |\phi ⟩=0$
$(3)$ 态矢 $|\psi ⟩$的归一性，记为：$⟨\psi |\psi ⟩=1$

\qquad
$\bullet$　算符与可观测量$\text{(Observable)}$
\qquad
\qquad 在量子力学中，用算符来表示微观粒子的力学量。对一个可观测的力学量进行测量，其结果都是实数。因此，与可观测量相对应的算符都是厄密算符。

\qquad 把一个一般的力学量 $A$（比如位置、动量、角动量、能量）所对应的厄密算符写成 $\hat{A}$，则有本征方程 $\hat{A}|{\psi }_n⟩=a_n|{\psi }_n⟩$，其中 $a_n$ 为本征值，$|{\psi }_n⟩$ 为本征矢量。
$(1)$ 本征值是实数：$a_n=a_n^{\ast }$，此处为复数共轭$\text{(C.c.)}$
$(2)$ 属于不同本征值的本征矢相互正交：$⟨{\psi }_n|{\psi }_m⟩=0$
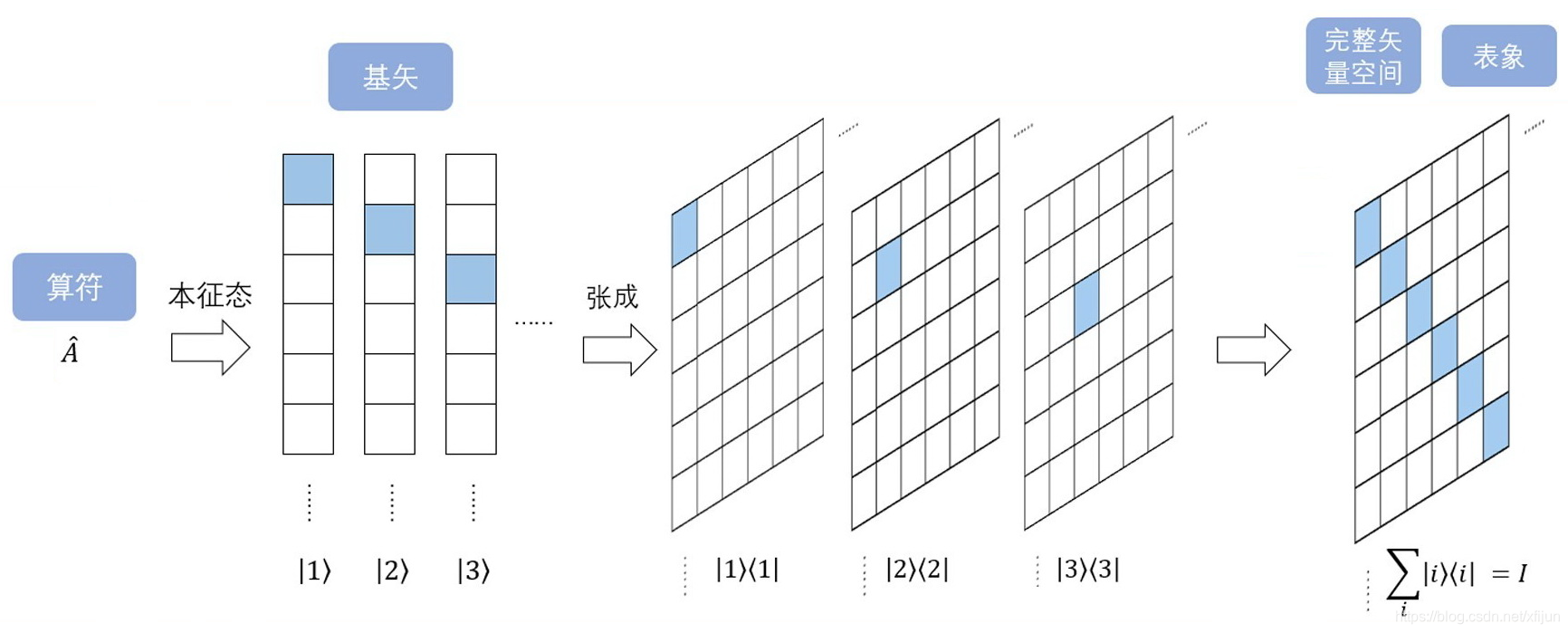
$(3)$ 本征矢的完备性条件：${\sum }_n|{\psi }_n⟩⟨{\psi }_n|=I$

$\Rightarrow$　由完备性条件，任意态矢 $|\psi ⟩$ 可由算符的本征矢展开为：

$|\psi ⟩=\sum _n|{\psi }_n⟩⟨{\psi }_n|\psi ⟩=\sum _n{c}_n|{\psi }_n⟩,c_n=⟨{\psi }_n|\psi ⟩$

图片引自https://zhuanlan.zhihu.com/p/183187859

\qquad
$\Rightarrow$　若态矢 $|\psi ⟩$ 已经归一化，则

$⟨\psi |\psi ⟩=\sum _m\sum _n{c}_m^{\ast }{c}_n⟨m|n⟩=\sum _m\sum _n{c}_m^{\ast }{c}_n{\delta }_{mn}=\sum _n{c}_n^{\ast }{c}_n=\sum _n|c_n{|}^2=1$
\qquad 　　 其中，$c_n^{\ast }{c}_n=|c_n{|}^2$ 表示当量子体系处于量子态 $|\psi ⟩$ 时，测量力学量 $A$ 取值为 $a_n$ 的概率。
\qquad
$\Rightarrow$　力学量 $A$ 在态 $|\psi ⟩$ 中的期望值为 $⟨A⟩=⟨\psi |\hat{A}|\psi ⟩$

在全同体系组成的系综中，每个体系都处于相同的 $|\psi ⟩$ 态，每次测量都可能会得到不同结果。期望值就是对含有相同体系的系综中不同体系的重复测量的平均值。
期望值不是对同一个体系的重复测量，对同一个体系进行重复测量会导致波函数的坍缩。

\qquad
\qquad 因此，力学量算符的本征值就是力学量的实际可能值，实验测量只能测得本征值。

$(1)$ 若系统处于力学量算符 $\hat{A}$ 的本征态 $|{\psi }_n⟩$ ，则测量力学量 $A$ 得到相应的本征值 $a_n$ ，测量后系统仍处于本征态 $|{\psi }_n⟩$ ，这种情况下的测量结果是完全确定的，没有随机性。

$(2)$ 若系统处于线性叠加态 $|\psi ⟩={\sum }_n{c}_n|{\psi }_n⟩$，则测量力学量 $A$ 时以概率 $|c_n{|}^2$ 得到本征值 $a_n$，若测量得到了本征值 $a_n$，则测量后系统坍缩到相应的本征态 $|{\psi }_n⟩$，再次测量均为本征值 $a_n$，也就是由于测量导致了波函数的坍缩$\text{(collapse)}$。

采用一般的写法：$\hat{A}{\psi }_n=a_n{\psi }_n$，其解为：$\{\begin{array}{l}\psi ={\psi }_1,{\psi }_2,\cdots ,{\psi }_n,\cdots \\ a=a_1,a_2,\cdots ,a_n,\cdots \end{array}$
（1）如果粒子刚好处于某个本征态 ${\psi }_n$，则力学量的取值就是相应的本征值 $a_n$
（2）如果粒子处于线性叠加态 $\psi ={\sum }_n{c}_n{\psi }_n$，则测量力学量会以概率 $|c_n{|}^2$ 得到本征值 $a_n$
　
若要求任何状态的波函数 $\psi$ 能够表示成 $\psi ={\sum }_n{c}_n{\psi }_n$，则 ${\psi }_1,{\psi }_2,\cdots ,{\psi }_n,\cdots$ 必须是完备函数系（也称完全系）。这就要求力学量算符 $\hat{A}$ 必须是厄密算符，因为厄米算符（对应于不同特征值）的本征函数是相互正交的。满足这个条件的算符所代表的力学量，就称为可观测量$\text{(Observable)}$。

\qquad
$\bullet$　表象$\text{(representation)}$

\qquad 表象的引入从某一力学量算符出发。

离散表象
\qquad
\qquad 假设某一力学量算符 $\hat{A}$ 的本征方程为 $\hat{A}|{\psi }_n⟩=a_n|{\psi }_n⟩$，将 $\hat{A}$ 的正交归一的本征态 { ∣ ψ n ⟩ } \{\vert\psi_n\rangle\} {∣ψn​⟩} 简记为 { ∣ n ⟩ } \{\vert n\rangle\} {∣n⟩}。

\qquad 以 { ∣ n ⟩ } \{\vert n\rangle\} {∣n⟩} 作为基矢，就可张起一个完备的矢量空间（希尔伯特空间），用该空间中的基矢 { ∣ n ⟩ } \{\vert n\rangle\} {∣n⟩} 来表示其他量子态与力学量算符，称为 $A$ 表象。

\qquad 在离散表象 $A$ 中，任意态矢 $|\psi ⟩$ 可由基矢 { ∣ n ⟩ } \{\vert n\rangle\} {∣n⟩} 的线性叠加 $|\psi ⟩={\sum }_n{c}_n|n⟩$ 构成，系数 $c_n=⟨n|\psi ⟩$ 为态矢 $|\psi ⟩$ 在基矢 $|n⟩$ 上的投影，满足归一化条件 ${\sum }_n|c_n{|}^2=1$ 。由于作为基矢的 { ∣ n ⟩ } \{\vert n\rangle\} {∣n⟩} 是已知的，知道了 { c n } \{c_n\} {cn​} 就知道了 $|\psi ⟩$。

\qquad 将 $c_n$ 排成列矢量，就表示态矢 $|\psi ⟩$ 在（离散）表象 $A$ 中的“波函数” $\psi (A)$：

$\psi (A)\equiv \left[\begin{array}{c}⟨1|\psi ⟩\\ ⟨2|\psi ⟩\\ ⋮\\ ⟨n|\psi ⟩\\ ⋮\end{array}\right]=\left[\begin{array}{c}{c}_1\\ c_2\\ ⋮\\ c_n\\ ⋮\end{array}\right],{\psi }^{†}(A)\equiv [⟨\psi |1⟩⟨\psi |2⟩\cdots ⟨\psi |n⟩\cdots ]=[c_1^{\ast }{c}_2^{\ast }\cdots c_n^{\ast }\cdots ]$

$\psi (A)$ 为态矢 $|\psi ⟩$ 在表象 $A$ 中“波函数”。
$\psi (A)$ 是列矢量，是态矢 $|\psi ⟩$ 在表象 $A$ 中的矩阵表示；${\psi }^{†}(A)$ 是行矢量，是 $⟨\psi |$ 在表象 $A$ 中的矩阵表示。

\qquad 一个微观量子态用抽象的态矢 $|\psi ⟩$ 描述，与表象无关；态矢 $|\psi ⟩$ 在某表象基矢上的投影，就是态矢 $|\psi ⟩$ 在该表象的波函数。使用狄拉克符号可以使得“态矢”与“波函数”区分开来。

同一个态 $|\psi ⟩$ 在不同的表象中用“波函数”来描写。所选取的表象不同，波函数的形式也不同，但它们描写的是同一个量子态
（1）选取一个特定的表象 $A$，就相当于选取了一个特定的坐标系，该坐标系由表象 $A$ 的本征矢 { ∣ n ⟩ } \{\vert n\rangle\} {∣n⟩} 作为基矢
（2）波函数中的 $c_1,c_2,\cdots ,c_n,\cdots$ 是态矢 $|\psi ⟩$ 在表象 $A$ 中沿各基矢 $|n⟩$ 方向的“分量”

\qquad
连续表象

\qquad 以一维运动为例，粒子的位置算符记为 $\hat{x}$，其本征值为 $x,x^{\prime },x^{\prime \prime },\cdots$，相应的本征矢记为 $|x⟩,|x^{\prime }⟩,|x^{\prime \prime }⟩,\cdots$，满足本征方程：

$\hat{x}|x⟩=x|x⟩,\hat{x}|x^{\prime }⟩=x^{\prime }|x^{\prime }⟩$

\qquad 由于本征值可以连续变化，因此 $x$ 表象是连续表象。

\qquad 连续变量 $x$ 表象中：
$(1)$ 完备性条件为 $\int \mathrm{d}x|x⟩⟨x|=I$。
\qquad 　　任意态矢 $|\psi ⟩$ 可以展开为：$|\psi ⟩=\int \mathrm{d}x|x⟩⟨x|\psi ⟩=\int \mathrm{d}x|x⟩\psi (x)$
\qquad 　　其中 $\psi (x)=⟨x|\psi ⟩$ 是态矢 $|\psi ⟩$ 在 $x$ 表象中的波函数。

$(2)$ 正交性为 $⟨x|x^{\prime }⟩=\delta (x-x^{\prime })$

$(3)$ 归一化条件 $⟨\psi |\psi ⟩=1$

$\begin{array}{rl}⟨\psi |\psi ⟩& =⟨\psi |\int \mathrm{d}x|x⟩⟨x|\psi ⟩\\ & =\int \mathrm{d}x⟨\psi |x⟩⟨x|\psi ⟩\\ & =\int \mathrm{d}x{\psi }^{\ast }(x)\psi (x)\\ & =\int \mathrm{d}x|\psi (x){|}^2=1\end{array}$
\qquad 其中，$|\psi (x){|}^2$ 为概率密度，${\psi }^{\ast }(x)\psi (x)\mathrm{d}x$ 表示体系处于量子态 $|\psi ⟩$ 时 $\hat{x}$ 的本征值在 $(x,x+\mathrm{d}x)$ 之间的的概率。

常用的连续表象有：坐标表象、动量表象
常用的离散表象有：能量表象、角动量表象

\qquad

6. 量子力学的矩阵表示

\qquad 选定某一个力学量 $A$，代表它的线性厄密算符 $\hat{A}$ 的本征方程为 $\hat{A}|n⟩=a_n|n⟩$，算符 $\hat{A}$ 的正交归一的本征态为 { ∣ n ⟩ } \{\vert n\rangle\} {∣n⟩}，特征值为 $a_n$，即包含如下关系：

$\{\begin{array}{l}\hat{A}|n⟩=a_n|n⟩,⟨n|{\hat{A}}^{†}=⟨n|a_n\\ |\psi ⟩={\sum }_n{c}_n|n⟩,c_n=⟨n|\psi ⟩,c_n^{\ast }=⟨\psi |n⟩\\ ⟨n|k⟩={\delta }_{nk}\\ {\sum }_n|n⟩⟨n|=I\\ ⟨\psi |\psi ⟩=1\end{array}$

\qquad
$\bullet$线性算符的矩阵表示
\qquad
\qquad 假设任意力学量算符 $\hat{F}$ 作用于归一化的态矢 $|\psi ⟩$ 后变成了态矢 $|\varphi ⟩$，即 $\hat{F}|\psi ⟩=|\varphi ⟩$。令态矢 $|\psi ⟩$ 在表象 $A$ 中的波函数为 $\psi (A)$，态矢 $|\varphi ⟩$ 在表象 $A$ 中的波函数为 $\varphi (A)$，也就是

$|\psi ⟩={\sum }_n{c}_n|n⟩,\psi (A)\equiv \left[\begin{array}{c}⟨1|\psi ⟩\\ ⟨2|\psi ⟩\\ ⋮\\ ⟨n|\psi ⟩\\ ⋮\end{array}\right]=\left[\begin{array}{c}{c}_1\\ c_2\\ ⋮\\ c_n\\ ⋮\end{array}\right]$

$|\varphi ⟩={\sum }_m{b}_m|m⟩,\varphi (A)\equiv \left[\begin{array}{c}⟨1|\varphi ⟩\\ ⟨2|\varphi ⟩\\ ⋮\\ ⟨m|\varphi ⟩\\ ⋮\end{array}\right]=\left[\begin{array}{c}{b}_1\\ b_2\\ ⋮\\ b_m\\ ⋮\end{array}\right]$

\qquad 算符 $\hat{F}$ 在离散表象 $A$ 中表现为一个矩阵 $F(A)$，记为 $[F]$，那么：

$[F]\psi (A)=\left[\begin{array}{cccccc}{F}_{11}& F_{12}& \cdots & F_{1n}& \cdots & \\ F_{21}& F_{22}& \cdots & F_{2n}& \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \\ F_{m1}& F_{m2}& \cdots & F_{mn}& \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \end{array}\right]\left[\begin{array}{c}{c}_1\\ c_2\\ ⋮\\ c_n\\ ⋮\end{array}\right]=\left[\begin{array}{c}{b}_1\\ b_2\\ ⋮\\ b_m\\ ⋮\end{array}\right]=\varphi (A)$
\qquad
\qquad 矩阵运算中 $b_m={\sum }_n{F}_{mn}{c}_n$，可得到矩阵 $F(A)$ 的矩阵元为 $F_{mn}=⟨m|\hat{F}|n⟩$

将 $\hat{F}|\psi ⟩=|\varphi ⟩$ 两边左乘 $⟨m|$，那么 $⟨m|\hat{F}|\psi ⟩=⟨m|\varphi ⟩$，可以在 $⟨m|\hat{F}|\psi ⟩$ 中插入完备性条件 ${\sum }_n|n⟩⟨n|=I$
　
$b_m=⟨m|\varphi ⟩=⟨m|\hat{F}|\psi ⟩=⟨m|\hat{F}{\sum }_n|n⟩⟨n|\psi ⟩={\sum }_n⟨m|\hat{F}|n⟩c_n$，比较可得 $F_{mn}=⟨m|\hat{F}|n⟩$

\qquad
\qquad 特别地，算符 $\hat{A}$ 本身在表象 $A$ 中的矩阵元为 $A_{mn}=⟨m|\hat{A}|n⟩=a_n⟨m|n⟩=a_n{\delta }_{mn}$，表示成矩阵为：

$[A]=\left[\begin{array}{cccccc}{a}_1& 0& \cdots & 0& \cdots & \\ 0& a_2& \cdots & 0& \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \\ 0& 0& \cdots & a_m& \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \end{array}\right]$

矩阵元也可以通过插入两个完备性条件 ${\sum }_m|m⟩⟨m|=I$ 和 ${\sum }_n|n⟩⟨n|=I$ 来得到，也就是：
　
$(1)$ 算符 $\hat{F}$ 的矩阵表示 $F(A)={\sum }_m|m⟩⟨m|\hat{F}{\sum }_n|n⟩⟨n|={\sum }_{m,n}⟨m|\hat{F}|n⟩|m⟩⟨n|$
　
$(2)$ 算符 $\hat{A}$ 本身的矩阵表示 $[A]={\sum }_{m,n}⟨m|\hat{A}|n⟩|m⟩⟨n|={\sum }_{m,n}{a}_n{\delta }_{mn}|m⟩⟨n|={\sum }_n{a}_n|n⟩⟨n|$

\qquad
\qquad
$\bullet$平均值公式及矩阵表示

\qquad 在表象 $A$ 中，仍然假设归一化态矢 $|\psi ⟩={\sum }_n{c}_n|n⟩$，力学量 $A$ 在态 $|\psi ⟩$ 中的期望值为 $⟨A⟩=⟨\psi |\hat{A}|\psi ⟩$。

$\begin{array}{rl}⟨A⟩=\sum _n{a}_n{c}_n^{\ast }{c}_n& =\sum _n{a}_n{c}_n⟨\psi |n⟩,c_n^{\ast }=⟨\psi |n⟩\\ & =\sum _n⟨\psi |c_n{a}_n|n⟩,\hat{A}|n⟩=a_n|n⟩\\ & =⟨\psi |\sum _n{c}_n\hat{A}|n⟩\\ & =⟨\psi |\hat{A}\sum _n{c}_n|n⟩\\ & =⟨\psi |\hat{A}|\psi ⟩\end{array}$

\qquad 由于算符 $\hat{A}$ 本身在表象 $A$ 中的矩阵元为 $A_{mn}=⟨m|\hat{A}|n⟩=a_n{\delta }_{mn}$，表示成矩阵形式为：

$\begin{array}{rl}⟨A⟩=\sum _n{a}_n{c}_n^{\ast }{c}_n& =[c_1^{\ast }{c}_2^{\ast }\cdots c_n^{\ast }\cdots ]\left[\begin{array}{cccccc}{a}_1& 0& \cdots & 0& \cdots & \\ 0& a_2& \cdots & 0& \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \\ 0& 0& \cdots & a_n& \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \end{array}\right]\left[\begin{array}{c}{c}_1\\ c_2\\ ⋮\\ c_n\\ ⋮\end{array}\right]\\ & ={\psi }^{†}(A)[A]\psi (A)\end{array}$

由于 $c_n^{\ast }{c}_n=|c_n{|}^2$ 表示体系处于量子态 $|\psi ⟩$ 时测量力学量 $A$ 取值为 $a_n$ 的概率，$⟨A⟩={\sum }_n|c_n{|}^2{a}_n$ 就是求数学期望

\qquad
\qquad 在表象 $A$ 中，对于任意力学量算符 $\hat{F}$，可观测量 $F$ 在态 $|\psi ⟩$ 中的期望值仍然为 $⟨F⟩=⟨\psi |\hat{F}|\psi ⟩$。

$\begin{array}{rl}⟨F⟩=⟨\psi |\hat{F}|\psi ⟩& =⟨\psi |\sum _m|m⟩⟨m|\hat{F}\sum _n|n⟩⟨n|\psi ⟩\\ & =\sum _m⟨\psi |m⟩⟨m|\hat{F}\sum _n|n⟩c_n\\ & =\sum _{m,n}{c}_m^{\ast }{c}_n⟨m|\hat{F}|n⟩=[c_1^{\ast }\cdots c_n^{\ast }\cdots ][F]\left[\begin{array}{c}{c}_1\\ c_2\\ ⋮\\ c_n\\ ⋮\end{array}\right]\\ & ={\psi }^{†}(A)F(A)\psi (A)\end{array}$

算符 $\hat{F}$ 所对应矩阵 $F(A)$ 的矩阵元为 $F_{mn}=⟨m|\hat{F}|n⟩$

\qquad

7. 表象变换

\qquad 态矢之间的基矢可以有多种选择。

$\bullet$假设力学量 $A$ 对应的线性厄密算符为 $\hat{A}$，其正交归一的本征矢 { ψ n } \{\psi_n\} {ψn​}，满足：

$⟨{\psi }_n|{\psi }_k⟩={\delta }_{nk},{\sum }_n|{\psi }_n⟩⟨{\psi }_n|=I,⟨\psi |\psi ⟩=1$

\qquad 　　态矢 $|\psi ⟩$ 在 $A$ 表象中展开为 $|\psi ⟩=\sum _n|{\psi }_n⟩⟨{\psi }_n|\psi ⟩=\sum _n{c}_n|{\psi }_n⟩,c_n=⟨{\psi }_n|\psi ⟩$

\qquad 　　由 { c n } \{c_n\} {cn​} 组成的列矢量是态矢 $|\psi ⟩$ 在 $A$ 表象中的波函数：

$\psi (A)\equiv \left[\begin{array}{c}{c}_1\\ c_2\\ ⋮\\ c_n\\ ⋮\end{array}\right],{\psi }^{†}(A)\equiv [c_1^{\ast }{c}_2^{\ast }\cdots c_n^{\ast }\cdots ]$

\qquad 　　任意线性算符 $F$ 在 $A$ 表象中的矩阵表示为 $F(A)$，其矩阵元为 $F_{mn}=⟨{\psi }_m|\hat{F}|{\psi }_n⟩$。

\qquad
$\bullet$另选一个力学量 $R$ 所对应线性厄密算符为 $\hat{R}$，其正交归一的本征矢 { ϕ ν } \{\phi_{\nu}\} {ϕν​}，满足：

$⟨{\varphi }_{\nu }|{\varphi }_{\mu }⟩={\delta }_{\nu \mu },{\sum }_{\nu }|{\varphi }_{\nu }⟩⟨{\varphi }_{\nu }|=I,⟨\psi |\psi ⟩=1$

\qquad 　　态矢 $|\psi ⟩$ 在 $R$ 表象中展开为：$|\psi ⟩=\sum _{\nu }|{\varphi }_{\nu }⟩⟨{\varphi }_{\nu }|\psi ⟩=\sum _{\nu }{a}_{\nu }|{\varphi }_{\nu }⟩,a_{\nu }=⟨{\varphi }_{\nu }|\psi ⟩$

\qquad 　　由 { a ν } \{a_{\nu}\} {aν​} 组成的列矢量就是态矢 $|\psi ⟩$ 在 $R$ 表象中的波函数：

$\psi (R)\equiv \left[\begin{array}{c}{a}_1\\ a_2\\ ⋮\\ a_{\nu }\\ ⋮\end{array}\right],{\psi }^{†}(R)\equiv [a_1^{\ast }{a}_2^{\ast }\cdots a_{\nu }^{\ast }\cdots ]$

\qquad 　　任意线性算符 $F$ 在 $R$ 表象中的矩阵表示为 $F(R)$，其矩阵元为 $F_{\mu \nu }=⟨{\varphi }_{\mu }|\hat{F}|{\varphi }_{\nu }⟩$。

\qquad
$\bullet$同一态矢 $|\psi ⟩$ 在 $A$ 和 $R$ 表象之间可通过变换矩阵 $S$ 联系起来，即 $\psi (R)=S\psi (A)$，表示成矩阵运算为：

$\left[\begin{array}{c}{a}_1\\ a_2\\ ⋮\\ a_{\nu }\\ ⋮\end{array}\right]=\underset{[S]}{\underbrace{\left[\begin{array}{cccccc}{S}_{11}& S_{12}& \cdots & S_{1n}& \cdots & \\ S_{21}& S_{22}& \cdots & S_{2n}& \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \\ S_{\nu 1}& S_{\nu 2}& \cdots & S_{\nu n}& \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \end{array}\right]}}\left[\begin{array}{c}{c}_1\\ c_2\\ ⋮\\ c_n\\ ⋮\end{array}\right]$，此处 $\{\begin{array}{l}{a}_{\nu }=⟨{\varphi }_n|\psi ⟩\\ c_n=⟨{\psi }_n|\psi ⟩\end{array}$

\qquad 显然有 $a_{\nu }=\sum _n{S}_{\nu n}{c}_n$，又由于 $⟨{\varphi }_{\nu }|=\sum _n⟨{\varphi }_{\nu }|{\psi }_n⟩⟨{\psi }_n|$，可得到

$\{\begin{array}{ll}{a}_{\nu }=\sum _n{S}_{\nu n}{c}_n& ⟹⟨{\varphi }_{\nu }|\psi ⟩=\sum _n{S}_{\nu n}⟨{\psi }_n|\psi ⟩\\ ⟨{\varphi }_{\nu }|=\sum _n⟨{\varphi }_{\nu }|{\psi }_n⟩⟨{\psi }_n|& ⟹⟨{\varphi }_{\nu }|\psi ⟩=\sum _n⟨{\varphi }_{\nu }|{\psi }_n⟩⟨{\psi }_n|\psi ⟩\end{array}$

\qquad 对比可得到 $S_{\nu n}=⟨{\varphi }_{\nu }|{\psi }_n⟩$。

变换矩阵 $S$ 完全由基矢 { ψ n } \{\psi_n\} {ψn​} 和 { ϕ ν } \{\phi_{\nu}\} {ϕν​} 的相互关系决定，而与态矢 $|\psi ⟩$ 无关。

\qquad 变换矩阵 $S$ 的厄密共轭矩阵 $S^{†}$ 的矩阵元为 $S_{n\nu }^{†}=(S_{\nu n}{)}^{\ast }=⟨{\varphi }_{\nu }|{\psi }_n{⟩}^{\ast }=⟨{\psi }_n|{\varphi }_{\nu }⟩$，可得到：

$\{\begin{array}{l}[S^{†}S{]}_{nm}=\sum _{\nu }{S}_{n\nu }^{†}{S}_{\nu m}=\sum _{\nu }⟨{\psi }_n|{\varphi }_{\nu }⟩⟨{\varphi }_{\nu }|{\psi }_m⟩=⟨{\psi }_n|{\psi }_m⟩={\delta }_{nm}\\ \\ [S{S}^{†}{]}_{\nu \mu }=\sum _n{S}_{\nu n}{S}_{n\mu }^{†}=\sum _n⟨{\varphi }_{\nu }|{\psi }_n⟩⟨{\psi }_n|{\varphi }_{\mu }⟩=⟨{\varphi }_{\nu }|{\varphi }_{\mu }⟩={\delta }_{\nu \mu }\end{array}$

\qquad 因此，$S{S}^{†}=S^{†}S=I$ 都是单位矩阵（恒等算符），并且将 $S$ 与 $S^{†}$ 称为幺正矩阵$\text{(unitary matrix)}$。

\qquad
结论1：若有表象之间的变换关系 $\psi (R)=S\psi (A)$，那么存在以下关系：

$\psi (R)=S\psi (A)⟹\psi (A)=S^{†}\psi (R)$　　 （两边左乘 $S^{†}$）
${\psi }^{†}(R)={\psi }^{†}(A)S^{†}⟹{\psi }^{†}(A)={\psi }^{†}(R)S$　　（两边右乘 $S$）

表象的幺正变换实际上就是线性代数中“正交变换”概念，幺正矩阵就是（互相正交的特征向量作为列矢量的）正交矩阵

\qquad
结论2：任意线性算符 $\hat{F}$ 在 $A$ 表象中的矩阵表示为 $F(A)$，矩阵元为 $F_{mn}=⟨{\psi }_m|\hat{F}|{\psi }_n⟩$；在 $R$ 表象中的矩阵表示为 $F(R)$，矩阵元为 $F_{\mu \nu }=⟨{\varphi }_{\mu }|\hat{F}|{\varphi }_{\nu }⟩$。
\qquad
\qquad 根据 $\{\begin{array}{l}{S}_{\nu n}=⟨{\varphi }_{\nu }|{\psi }_n⟩\\ S_{n\nu }^{†}=⟨{\psi }_n|{\varphi }_{\nu }⟩\end{array}$，可得到：$F(R)=SF(A)S^{†}$ 或 $F(A)=S^{†}F(R)S$

此处的矩阵乘法 $F(R)=SF(A)S^{†}$ 相当于矩阵元的计算：
　
$\begin{array}{rl}{F}_{\mu \nu }=⟨{\varphi }_{\mu }|\hat{F}|{\varphi }_{\nu }⟩& =⟨{\varphi }_{\mu }|\sum _n|{\psi }_n⟩⟨{\psi }_n|\hat{F}\sum _m|{\psi }_m⟩⟨{\psi }_m||{\varphi }_{\nu }⟩\\ & =\sum _n\sum _m{S}_{\mu n}⟨{\psi }_n|\hat{F}|{\psi }_m⟩S_{m\nu }^{†}\\ & =\sum _n\sum _m{S}_{\mu n}{F}_{nm}{S}_{m\nu }^{†}\end{array}$

\qquad
结论3：表象变换时，态矢和算符的具体矩阵表示与所选择的表象有关，但它们描述的物理内容不受表象选择的影响。
$(1)$ 态矢的模方不变
$⟨\psi |\psi ⟩={\psi }^{†}(A)\psi (A)={\psi }^{†}(R)S{S}^{†}\psi (R)={\psi }^{†}(R)\psi (R)$
$⟨\psi |\varphi ⟩={\psi }^{†}(A)\varphi (A)={\psi }^{†}(R)S{S}^{†}\varphi (R)={\psi }^{†}(R)\varphi (R)$

$(2)$力学量算符的本征值与表象选择无关
$$\begin{gathered} F(A){\psi }_{\lambda }(A)=\lambda {\psi }_{\lambda }(A)\to S^{†}F(R)S{S}^{†}{\psi }_{\lambda }(R)=\lambda S^{†}{\psi }_{\lambda }(R) \\ \to F(R){\psi }_{\lambda }(R)=\lambda {\psi }_{\lambda }(R) \end{gathered}$$

$(3)$平均值公式不变 $⟨F⟩=⟨\psi |\hat{F}|\psi ⟩$
$$\begin{gathered} ⟨F⟩=⟨\psi |\hat{F}|\psi ⟩={\psi }^{†}(A)F(A)\psi (A)={\psi }^{†}(R)S{S}^{†}F(R)S{S}^{†}\psi (R) \\ \to ⟨F⟩={\psi }^{†}(R)F(R)\psi (R) \end{gathered}$$

$(4)$算符之间的相互关系不变
\qquad\qquad 若$\hat{F}=\hat{P}\hat{Q}$，那么 $F(A)=P(A)Q(A)=P(R)Q(R)=F(R)$

\qquad
主要参考书籍：
[1] Griffith. 量子力学概论
[2] 钱伯初. 量子力学
[3] 周世勋. 量子力学教程