ACM知识点 之 贪心（3）区间选点问题

版权声明：本文为博主原创文章，转载须注明地址：http://blog.csdn.net/liuxucoder

区间选点的问题大致可以描述为： 
给定N个区间[a,b]，取尽量少的点，使得每个区间内都至少有一个点（不同区间内含的点可以重复）。

关于贪心算法的验证过程就不再赘述，现在思考一下贪心策略的制定。 
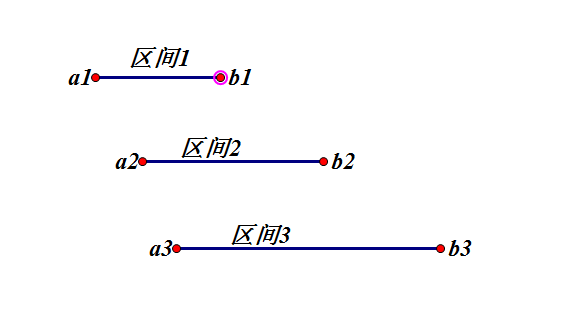
对于区间[a1, b1] 、[a2, b2]、 [a3, b3] 来说， 
如果想选择最少的点，那么必须选择每个区间的右端点，示意图如下： 

当你每一次都选择区间的最右端，才能保证每一个选的点覆盖的范围都是最广泛的，也就是说选的点才是最少的。

和之前不相交区间的思考方法类似，把区间进行预处理，按照端点的大小排序（同样，按照右端点排序会好理解一点，但是左端点排序一样可以起到作用，初学者不必迷信右端点排序）。 
预处理过后，求解策略的思路和求不相交区间相似，如果下一个区间的左端点不被覆盖，则答案+1，如下：

while(剩余区间的数目不为0)
{
    if（找到符合条件的下一个区间）
    {
        当前区间 = 下一个区间；
        答案数+1；
    }

    区间数--；
}

---

看题：NYOJ 1036

                                    非洲小孩
                    时间限制：1000 ms  |  内存限制：65535 KB
                                    难度：2

描述 
家住非洲的小孩，都很黑。为什么呢？ 
第一，他们地处热带，太阳辐射严重。 
第二，他们不经常洗澡。（常年缺水，怎么洗澡。） 
现在，在一个非洲部落里，他们只有一个地方洗澡，并且，洗澡时间很短，瞬间有木有！！（这也是没有的办法，缺水啊！！） 
每个小孩有一个时间段能够洗澡。并且，他们是可以一起洗的（不管你是男孩是女孩）。 
那么，什么时间洗澡，谁应该来洗，由谁决定的呢？那必然是他们伟大的“澡”神啊。“澡”神有一个时间表，记录着该部落的小孩，什么时候段可以洗澡。现在，“澡”神要问你，一天内，他需要最少开启和关闭多少次洗澡的水龙头呢？因为，开启和关闭一次水龙头是非常的费力气的，即便，这也是瞬间完成的。

输入 
多组数据 
第一行一个n<=100。 
接下来n行，每行一个时间段。H1H1:M1M1-H2H2:M2M2，24小时制。 
保证该时间段是在一天之内的。但是，不保证，H1H1:M1M1先于H2H2:M2M2。

输出 
题目描述，“澡”神最少需要开启和关闭多少次水龙头呢？

样例输入 
1 
00:12-12:12 
2 
00:12-12:12 
14:00-12:00

样例输出 
1 
1

提示 
Ps：开启和关闭为一次

---

这道题是完美的区间选点，但是数据有坑（不保证H1H1:M1M1先于H2H2:M2M2。） 所以读入的时候要注意进行判断。

解决代码如下:

/*
************************************
    Title: NYOJ1036-非洲小孩
************************************
    Date：2015/07/23
************************************
    author：刘旭
************************************
Memory：256KB
Time：8ms
************************************
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

#define MAX 1005

struct Node
{
    int x;
    int y;
};

Node map[MAX];

bool cmp(Node a,Node b){
    if(a.y != b.y){
        return a.y < b.y;
    }

    return a.x < b.x;
}

int main()
{
    int num = 0;
    while(EOF != scanf("%d", &num)){
            memset(map, -1, sizeof(map));
            int a1,b1,a2,b2;

            for(int i = 0; i < num; i++){
                scanf("%d:%d-%d:%d",&a1,&b1,&a2,&b2);
                int key1 = a1*60+b1;
                int key2 = a2*60+b2;
                if(key1 > key2){
                    swap(key1, key2);
                }
                map[i].x = key1;
                map[i].y = key2;
            }

            sort(map, map+num, cmp);

            int start = map[0].y;
            int num_node = 0;
            int ans = 1;
            while(num - num_node){
                if(map[num_node].x > start){
                    start = map[num_node].y;
                    ans++;
                }

                num_node++;
            }

            printf("%d\n", ans);
    }

    return 0;
}