Codeforces Round #479 (Div. 3)——E. Cyclic Components【并查集判环】

E. Cyclic Components

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given an undirected graph consisting of $n$ vertices and $m$ edges. Your task is to find the number of connected components which are cycles.

Here are some definitions of graph theory.

An undirected graph consists of two sets: set of nodes (called vertices) and set of edges. Each edge connects a pair of vertices. All edges are bidirectional (i.e. if a vertex $a$ is connected with a vertex $b$, a vertex $b$ is also connected with a vertex $a$). An edge can't connect vertex with itself, there is at most one edge between a pair of vertices.

Two vertices $u$ and $v$ belong to the same connected component if and only if there is at least one path along edges connecting $u$ and $v$.

A connected component is a cycle if and only if its vertices can be reordered in such a way that:

• the first vertex is connected with the second vertex by an edge,
• the second vertex is connected with the third vertex by an edge,
• ...
• the last vertex is connected with the first vertex by an edge,
• all the described edges of a cycle are distinct.

A cycle doesn't contain any other edges except described above. By definition any cycle contains three or more vertices.

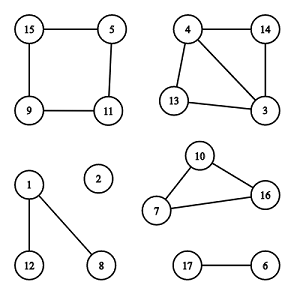There are $6$ connected components, $2$ of them are cycles: $[7,10,16]$ and $[5,11,9,15]$.

Input

The first line contains two integer numbers $n$ and $m$ ($1\le n\le 2\cdot {10}^5$, $0\le m\le 2\cdot {10}^5$) — number of vertices and edges.

The following $m$ lines contains edges: edge $i$ is given as a pair of vertices $v_i$, $u_i$ ($1\le v_i,u_i\le n$, $u_i\ne v_i$). There is no multiple edges in the given graph, i.e. for each pair ($v_i,u_i$) there no other pairs ($v_i,u_i$) and ($u_i,v_i$) in the list of edges.

Output

Print one integer — the number of connected components which are also cycles.

Examples

input

Copy

5 4
1 2
3 4
5 4
3 5

output

Copy

1

input

Copy

17 15
1 8
1 12
5 11
11 9
9 15
15 5
4 13
3 13
4 3
10 16
7 10
16 7
14 3
14 4
17 6

output

Copy

2

Note

In the first example only component $[3,4,5]$ is also a cycle.

The illustration above corresponds to the second example.

题目分析：就是让你判断有几个元素在一起可以组成一个单环（每个环里的每个元素的度数都为2），用并查集判环就行。

并查集判环：如果元素属于同一个根节点则可以成环。

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int pre[100010];
void init(int n){
	for(int i=0;i<=n;i++){
		pre[i]=i;
	}
} 
int find(int x){
	if(pre[x]==x) return x;
	else{
		pre[x]=find(pre[x]);
		return pre[x];
	}
}
int join(int x,int y){
	int fx=find(x),fy=find(y);
	if(fx!=fy){
		pre[fx]=fy;
		return 0;//如果两边的根节点相同则说明可以成环 
	}
	else return 1;
}
int du[1000010]; 
int main(){
	int n,m;
	while(~scanf("%d%d",&n,&m)){
		memset(du,0,sizeof(du)); 
		init(n);
		//int ans=0;
		int a[100010],b[100010];
		for(int i=1;i<=m;i++){
			scanf("%d %d",&a[i],&b[i]);
			du[a[i]]++;//记录每一条边的度数 
			du[b[i]]++; 
		}
		//如果只成一个单环则环内每一点的度数都为2 
		int cnt=0;
		for(int i=1;i<=m;i++){
			if(du[a[i]]==2&&du[b[i]]==2&&join(a[i],b[i])){
				cnt++;
			}
		}
		printf("%d\n",cnt); 
	}
	return 0;
}