需求分析
0.问题描述
小明和小芳出去乡村玩,小明负责开车,小芳来导航。
小芳将可能的道路分为大道和小道。大道比较好走,每走1公里小明会增加1的疲劳度。小道不好走,如果连续走小道,小明的疲劳值会快速增加,连续走s公里小明会增加s^2的疲劳度。
例如:有5个路口,1号路口到2号路口为小道,2号路口到3号路口为小道,3号路口到4号路口为大道,4号路口到5号路口为小道,相邻路口之间的距离都是2公里。如果小明从1号路口到5号路口,则总疲劳值为〖(2+2)〗2+2+22=16+2+4=22。
现在小芳拿到了地图,请帮助她规划一个开车的路线,使得按这个路线开车小明的疲劳度最小。
1.问题分析
要实现的功能:
1.通过键盘输入路口数量、道路数量以及道路信息(类型、长度、位置);
2.设计算法找到一条路线使疲劳值最小;
3.通过屏幕输出疲劳值。
疲劳值计算方法:
1).大路:疲劳值=公里数;
2).小路:疲劳值=连续的公里数的平方。
2.输入数据
输入的第一行包含两个整数n, m,分别表示路口的数量和道路的数量。路口由1至n 编号,小明需要开车从1号路口到n号路口。
接下来m行描述道路,每行包含四个整数t, a, b, c,表示一条类型为t,连接a与b 两个路口,长度为c公里的双向道路。其中t为0表示大道,t为1表示小道。保证1 号路口和n号路口是连通的。
2 ≤ n ≤ 8,1 ≤ m ≤ 10,1 ≤ a, b ≤ n,t是0或1,c ≤10^5 保证答案不超过 10^6。
3.输出数据
输出一个整数,表示最优路线下小明的疲劳度。
4.测试样例设计
样例一:不存在小道
输入:5 7
0 1 2 10
0 1 4 20
0 2 4 5
0 1 3 3
0 2 3 2
0 3 5 15
0 4 5 11
输出:18
样例二:所有的小道不相交
输入:6 7
0 1 2 4
1 2 3 2
0 1 4 2
1 1 5 3
0 4 5 2
0 5 6 10
0 3 6 8
输出:14
样例三:有多条连续的小道相连
输入:6 7
1 1 2 3
1 2 3 2
0 1 3 30
0 3 4 20
0 4 5 30
1 3 5 6
1 5 6 1
输出:76
样例四:边界条件最小值
输入:2 1
0 1 2 15
输出:15
样例五:全为小路
输入:5 7
1 1 2 10
1 1 4 20
1 2 4 5
1 1 3 3
1 2 3 2
1 3 5 15
1 4 5 11
输出:324
二、概要设计
1.抽象数据类型
每一个路口相当于一个顶点,每一条道路相当于一条边,每个路口可以和多个其他路口 关联成双向道路,因此符合网状逻辑结构的特征,故可以利用图(无向图)这种数据结 构。
数据对象:所有的路口以及道路
数据关系:所有路口之间都可以以不同的双向道路相连从而构成的带权无向图
基本操作:
1.准备能储存这组数据的空间
2.设置边的权重
3.获得边的权重
ADT Graph{
数据对象D:
顶点集V={vi|vi∈整数,i=1,2,… ,n,n∈整数}
弧集:E={e_ij| i,j∈V}
Graph=(V,E)
数据关系R:
VR={<v,w>| v,w∈V且P(v,w)∈E}
基本操作:
Graphm(int v); // 构造函数
~Graphm();//析构函数
void setEdge(int v1, int v2, long long wght);// 为边(v1,v2)设置权值为wght
long long weight(int v1, int v2);// 返回边(v1,v2)的权值
}
2.算法的基本思想
1.用两个图将大路和小路分别储存下来;
2.用floyd算法处理小路构成的图,找到只走小路时每两个路口之间的最短距离;
3.通过spfa算法记录大路和小路到达i点时的最小疲劳值;
4.如果到达i点的路是大路,那么它可以由大路转移过来,也可以由小路转移过来;
5.如果到达i点的路是小路,就只能由大路转移过来;
6.最终大路和小路到达i点最小疲劳值中的最小值就是所有路线中的最小疲劳值。
3.程序的流程
1.初始化模块:初始化两个图
2.归并模块:用FLoyd算法将走小路进行归并
3.spfa处理模块:用spfa算法分别记录大路和小路到达每个顶点时的最小疲劳值
4.比较模块:找到大路和小路到达终点最小疲劳值中的最小值,并通过屏幕显示结果
三、详细设计
1.物理数据类型
物理数据类型:顶点信息还有边权的数据类型都为整形int。
物理数据结构:因为要频繁的访问两个顶点间(边)的信息,所以用邻接矩阵(二维数 组)实现图,在图信息的存储和图遍历及图信息的读取上会带来很大的方便。
#define inf 0x3f3f3f3f
Graphm(int v) // 构造函数
{
int i, j;
numVertex = v;
numEdge = 0;
mark = new int[v];
for (i=0; i<numVertex; i++)
mark[i] = UNVISIT;
undirected = true;//初始化为无向图
//初始化邻接矩阵
matrix = (long long**) new long long*[numVertex];
for (i=0; i<numVertex; i++)
{
matrix[i] = new long long[numVertex];
}
for (i=0; i<numVertex; i++)
for (j=0; j<numVertex; j++)
matrix[i][j] = inf;//初始化权值为无穷大
}
~Graphm()//析构函数
{
delete []mark; //回收动态分配内存
for (int i=0; i<numVertex; i++)
delete []matrix[i];
delete []matrix;
}
void setEdge(int v1, int v2, long long wt)// 为边(v1,v2)设置权值为wt
{
if(matrix[v1][v2] == inf)
numEdge++;
matrix[v1][v2] = wt;
if(undirected)//无向图
matrix[v2][v1] = wt;
}
long long weight(int v1, int v2)// 返回边(v1,v2)的权值
{
return matrix[v1][v2];
}
2.输入和输出的格式
输入格式:
输入的第一行包含两个整数n, m,分别表示路口的数量和道路的数量。路口 由 1至n编号,小明需要开车从1号路口到n号路口。
接下来m行描述道路,每行包含四个整数t, a, b, c,表示一条类型为t,连接a与b 两个路口,长度为c公里的双向道路。其中t为0表示大道,t为1表示小道。保证1 号路口和n号路口是连通的。
输出格式:
输出一个整数,表示最优路线下小明的疲劳度。
3.算法的具体步骤
初始化模块:
void creat( )
{
//n为路口数,m为道路数 cin >> n >> m;
//创建n+1个顶点的图 Graphm *Gx = new Graphm(n+1);//储存小路构成的图
使图的顶点i为路口i Graphm *Gd = new Graphm(n+1);//储存大路构成的图
//初始化图为无向图
for (int i=0; i<m; i++){
//输入路口信息和道路 int a, b, c, d;
信息 cin >> a >> b >> c >> d;
if (a==1 && Gx->weight(b,c) > d) {
//给储存小路的图的边 Gx->setEdge(b,c,d);
赋权值 Gx->setEdge(c,b,d);
}
else if (a==0 && Gd->weight(b,c) > d){
//给储存大路的图的边 Gd->setEdge(b,c,d);
赋权值 Gd->setEdge(c,b,d);
}
}
}
归并模块:
void floyd(Graphm **G)//对路预处理
{
//遍历整个邻接矩阵 for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
//如果i到j的边的权重大于if( (*G)->weight(i,j) > (*G)->weight(i,k) + (*G)->weight(k,j)
边ik的权重加边kj的权重 &&(*G)->weight(i,k)!=inf&&(*G)->weight(k,j)!=inf ) {
//令边ij权重等于边ik的权 (*G)->setEdge(i,j, (*G)->weight(i,k) + (*G)->weight(k,j));
重加边kj的权重 }
}
}
spfa处理模块:
//dis1[i]和dis[2]分别来储存大 void SPFA( ){
路和小路到达i的最小疲劳值 long long dis1[100],dis2[100];
//vis[i]标记i是否在队列中 bool jl[100],vis[100];
//将dis1和dis2数组初值设 memset(dis1,inf,sizeof(dis1));
为无穷大 memset(dis2,inf,sizeof(dis2));
//队列q用于保存待优化结点 queue<int>q;
//将dis[源点]设为0 dis1[1]=dis2[1]=0;
q.push(1); vis[1]=1;
//实现spfa算法 while(!q.empty()){
int now=q.front();
q.pop();
vis[now]=0;
for(int i=1;i<=n;i++){
long long v = Gd->weight(now,i);
//大路转移到大路 if(dis1[i]>dis1[now]+v){
//松弛dis1[i] dis1[i] = dis1[now] + v;
if(vis[i]) continue;
vis[i] = 1;
q.push(i);
}
//小路转移到大路 if(dis1[i] > dis2[now] + v){
//松弛dis1[i] dis1[i] = dis2[now] + v;
if(vis[i]) continue;
vis[i] = 1;
q.push(i);
}
if(Gx->weight(now,i) < 1e10){
//计算小路的疲劳值 v = Gx->weight(now,i) * Gx->weight(now,i);
//大路转移到小路 if(dis2[i] > dis1[now] + v)
//松弛dis2[i] { dis2[i] = dis1[now] + v;
if (vis[i]) continue;
vis[i] = 1;
q.push(i); }
}
}}
}
比较模块:
//获取最小疲劳值 long long getResult( )
//大路和小路到达i点最小疲劳值 { return min(dis1[n],dis2[n]); }
中的最小值就是所有路线中的最小疲劳值。
4.算法的时空分析
初始化模块:
图的顶点和边权值的输入时空复杂度都为O(n)
除此之外对每个图信息输入的操作的时空复杂度都为O(1)
图边权值的设置时空复杂度为O(1)
spfa处理模块:
图边权获取时空复杂度为O(1)
由于每个顶点都要入队和出队,所以时间复杂度是O(n)
比较模块: 调用函数输出时空复杂度为 O(1)
四、调试分析
1.调试方案设计
调试目的:查看出错的地方在哪里
样例:6 7
1 1 2 3
1 2 3 2
0 1 3 30
0 3 4 20
0 4 5 30
1 3 5 6
1 5 6 1
调试计划:
1)设置断点
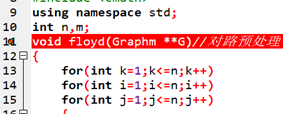
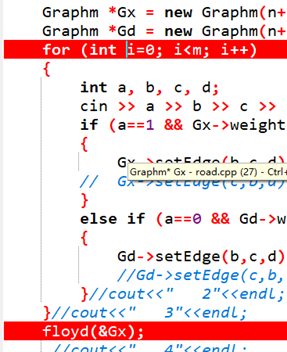
2)添加查看
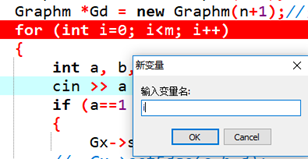
3)增加cout
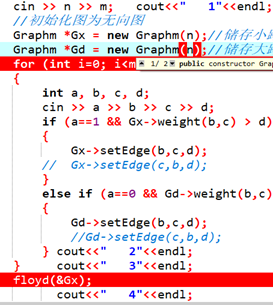
4)编译调试
2.调试过程和结果,及分析
调试结果:
分析:调试结果显示指针越界,显示屏显示到for循环结束就不再输出了,所以可推断出是for循环里面越界了,检查后发现是获取设置图中边的时候没有将下标-1,最后给图扩容+1就可以运行成功了。
五、测试结果
样例一:
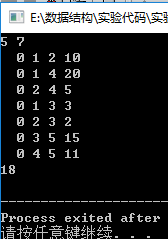
分析:从大道1走到大道3,再走到大道5, 疲劳值为3+15=18。
样例二:
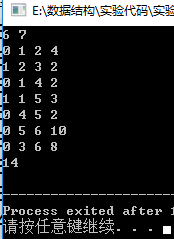
分析:走1到4的大路、4到5的大路、5到6的大路,最终疲劳值是2+2+10=14。
样例三:
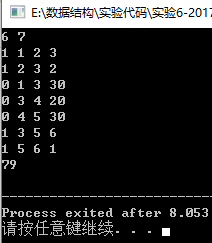
分析:从1走小道到2,再走小道到3,疲劳度为5^2=25;然后从3走大道经过4到达 5,疲劳度为20+30=50;最后从5走小道到6,疲劳度为1。总共为76。
样例四:
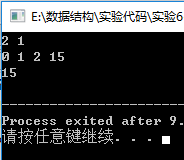
样例五:
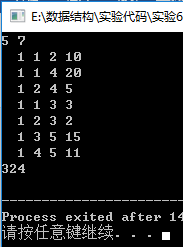
结果正确
六、实验日志(选做)
2018-12-03:去计算机职业资格认证官网查看17年3次考试中的第四题,最终确认题目为行车路线。
2018-12-04:去csdn上搜索代码,寻找思路。
2018-12-05:开始写实验报告的需求分析及概要设计。
2018-12-08:用图的ADT改写代码,出现了一些问题:1.在用实验5写的图的ADT的时候,构造函数中没有对图的类型进行初始化,建图的时候我也没有设置图的类型,导致在设置边权时出现了一些未知错误。2.我是通过邻接矩阵来储存图,初始化顶点距离为无穷远,但是没改变类中边权的返回类型以及一些函数的参数类型,编译器报错。3.没注意下标起始为0,指针越界,编译后结果不能输出。
2018-12-09:完善预习报告的剩余部
附代码:
Graphm.h
#ifndef _GRAPHM_H
#define _GRAPHM_H
#define inf 0x3f3f3f3f
#define VertexType int
#define M 100
#define UNVISIT 0
#define VISIT 1
class Graphm
{
private:
int numVertex, numEdge;
bool undirected;//true表示无向图
long long **matrix;
int *mark;
VertexType vexs[M];
public:
Graphm(int v); // 构造函数
~Graphm();//析构函数
int n();//返回节点数
int e();//返回边数
int first(int v);// 返回v的第一个邻居
int next(int v,int w);// 返回v的在w后的邻居
void setType(bool flag);//设置图的类型
bool getType(); //获取图的类型
int locateVex(VertexType u);//找到(包含实际信息的)顶点在图中的位置
VertexType getVex(int v);//返回某个顶点的值(实际信息)
void putVex(int v,VertexType value);//给某个顶点赋值
void setEdge(int v1, int v2, long long wght);// 为边(v1,v2)设置权值
void delEdge(int v1, int v2);//删除边(v1,v2)
bool isEdge(int i, int j);// 判断边(i,j)是否在图中
long long weight(int v1, int v2);// 返回边的权值
int getMark(int v) ;//取得顶点的标志位
void setMark(int v, int val);//设置顶点的标志位
};
#endif
Graphm.cpp
#include "Graphm.h"
#include <iostream>
#include <string.h>
using namespace std;
Graphm::Graphm(int v) // 构造函数
{
int i, j;
numVertex = v;
numEdge = 0;
mark = new int[v];
for (i=0; i<numVertex; i++)
mark[i] = UNVISIT;
undirected = true;//初始化为无向图
//初始化邻接矩阵
matrix = (long long**) new long long*[numVertex];
for (i=0; i<numVertex; i++)
{
matrix[i] = new long long[numVertex];
}
for (i=0; i<numVertex; i++)
for (j=0; j<numVertex; j++)
matrix[i][j] = inf;//初始化权值为无穷大
}
Graphm::~Graphm()//析构函数
{
delete []mark; //回收动态分配内存
for (int i=0; i<numVertex; i++)
delete []matrix[i];
delete []matrix;
}
int Graphm::n()//返回节点数
{
return numVertex;
}
int Graphm::e()//返回边数
{
return numEdge;
}
int Graphm::first(int v)// 返回v的第一个邻居
{
for (int i=0; i<numVertex; i++)
{
if (matrix[v][i]!=inf) return i;
}
return numVertex;//如果没有邻居,返回节点数
}
int Graphm::next(int v,int w)// 返回v的在w后的邻居
{
for (int i=w+1; i<numVertex; i++)
{
if (matrix[v][i]!=inf) return i;
}
return numVertex;//如果没有,返回节点数
}
void Graphm::setType(bool flag)//设置图的类型
{
undirected = flag;
}
bool Graphm::getType() //获取图的类型
{
return undirected;
}
int Graphm::locateVex(VertexType u)//找到(包含实际信息的)顶点在图中的位置
{
for (int i=0; i<numVertex; i++)
{
if (u == vexs[i])
return i;
}
return -1;
}
VertexType Graphm::getVex(int v)//返回某个顶点的值(实际信息)
{
return vexs[v];
}
void Graphm::putVex(int v,VertexType value)//给某个顶点赋值
{
vexs[v]=value;
}
void Graphm::setEdge(int v1, int v2, long long wt)// 为边(v1,v2)设置权值
{
if(matrix[v1][v2] == inf)
numEdge++;
matrix[v1][v2] = wt;
if(undirected)
matrix[v2][v1] = wt;
}
void Graphm::delEdge(int v1, int v2)//删除边(v1,v2)
{
if(matrix[v1][v2] != 0)
numEdge++;
matrix[v1][v2] = 0;
if(undirected)
matrix[v2][v1] = 0;
}
bool Graphm::isEdge(int i, int j)// 判断边(i,j)是否在图中
{
return matrix[i][j] != inf;
}
long long Graphm::weight(int v1, int v2)// 返回边的权值
{
return matrix[v1][v2];
}
int Graphm::getMark(int v)//取得顶点的标志位
{
return mark[v];
}
void Graphm::setMark(int v, int val)//设置顶点的标志位
{
mark[v] = val;
}
main.cpp
#include "Graphm.h"
#include <iostream>
#include <cstring>
#include <string>
#include <queue>
#include <stack>
#include <vector>
#include <cmath>
using namespace std;
int n,m;
void floyd(Graphm **G)//对路预处理
{
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
if((*G)->weight(i,j)>(*G)->weight(i,k)+(*G)->weight(k,j)&&(*G)->weight(i,k)!=inf&&(*G)->weight(k,j)!=inf)
{
(*G)->setEdge(i,j, (*G)->weight(i,k) + (*G)->weight(k,j));
}
}
}
int main()
{
cin >> n >> m;
//初始化图为无向图
Graphm *Gx = new Graphm(n+1);//储存小路构成的图
Graphm *Gd = new Graphm(n+1);//储存大路构成的图
for (int i=0; i<m; i++)
{
int a, b, c, d;
cin >> a >> b >> c >> d;
if (a==1 && Gx->weight(b,c) > d)
{
Gx->setEdge(b,c,d);
// Gx->setEdge(c,b,d);
}
else if (a==0 && Gd->weight(b,c) > d)
{
Gd->setEdge(b,c,d);
//Gd->setEdge(c,b,d);
}
}
floyd(&Gx);
long long dis1[100],dis2[100];
bool jl[100],vis[100];
memset(dis1,inf,sizeof(dis1));
memset(dis2,inf,sizeof(dis2));
queue<int>q;
dis1[1]=dis2[1]=0;
q.push(1);
vis[1]=1;
while(!q.empty())
{
int now=q.front();
q.pop();
vis[now]=0;
for(int i=1;i<=n;i++)
{
long long v = Gd->weight(now,i);
if(dis1[i]>dis1[now]+v)//大路加大路
{
dis1[i] = dis1[now] + v;
if(vis[i]) continue;
vis[i] = 1;
q.push(i);
}
if(dis1[i] > dis2[now] + v)//大路加小路
{
dis1[i] = dis2[now] + v;
if(vis[i]) continue;
vis[i] = 1;
q.push(i);
}
if(Gx->weight(now,i) < 1e10)
{
v = Gx->weight(now,i) * Gx->weight(now,i);
if(dis2[i] > dis1[now] + v)//小路加大路
{
dis2[i] = dis1[now] + v;
if (vis[i]) continue;
vis[i] = 1;
q.push(i);
}
}
}
}
cout << min(dis1[n],dis2[n]) << endl;
return 0;
}





















 834
834











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








