用L-型砖块铺砌正方形棋盘

在正文之前，我能不能先吐槽一下，上周算法老师布置了实验，其中有些题目只有一句话。如果这个题目比较特殊，一句话就知道是什么题义，那咱们也就不说什么了。你看哈，任务二：实现铺砖问题的算法。只有这样一句话，就没了，没有题义，所以要了解具体的题目要求，具体的输入输出，是不是就要问一下度娘，搜完之后，分为两种，一种是一维的铺砖问题，一种是二维的铺砖问题。我就想着我们这样的水平老师可能想让我们写一维的那个题。然后我就屁颠屁颠的写完然后提交了。

等到第二天老师上课的时候，老师就把这个铺砖问题说是怎样的，要怎样写。然后我就呆了，心里有一万句骂人的话，但是咱不敢说啊，/(ㄒoㄒ)/~~

说正事，铺砖问题：
在 2^n * 2^n 棋盘上任意除去一个方格，剩下的棋盘能够被L-型完全覆盖。这是一个定理，是已证明的。
我从网上下载了证明过程的PDF，给你们分享一下。



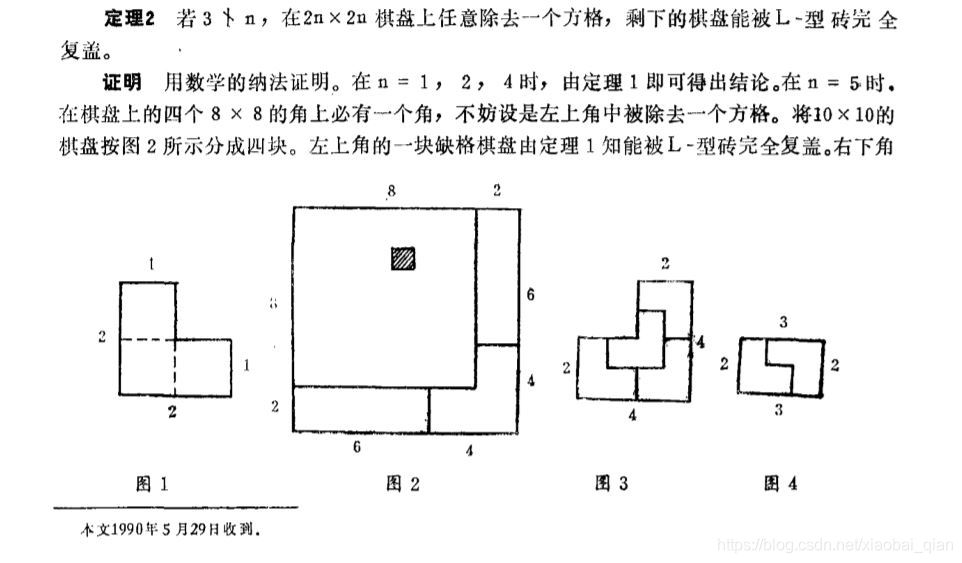
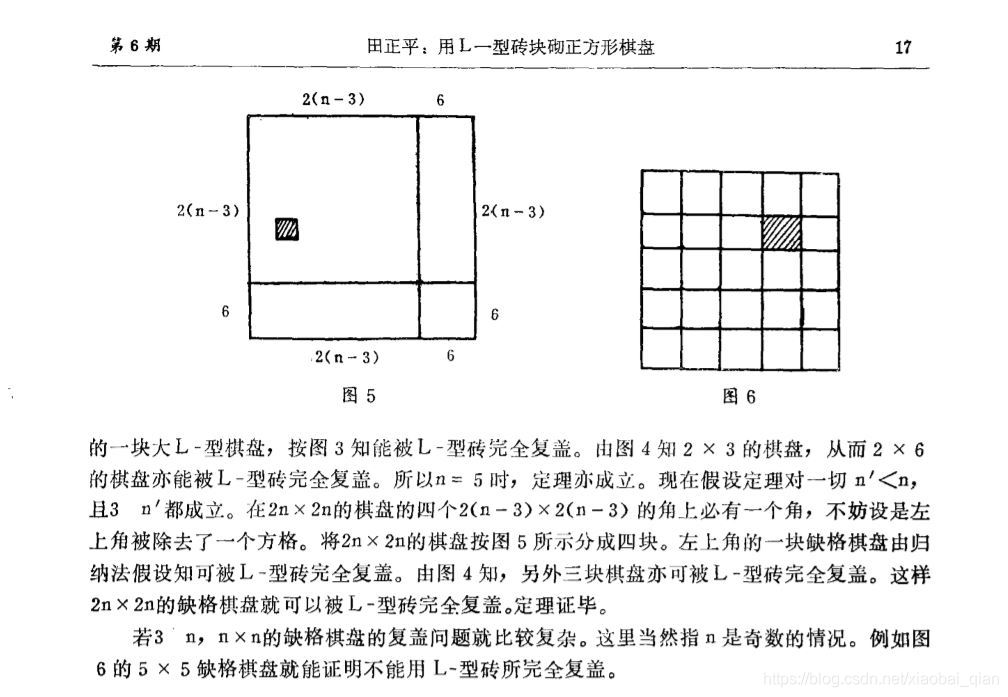
现在我们要做的是，输入棋盘的边长，（注意：边长是2^n）

输出是 2^n* 2^n这样一个二维数组，同一块L-型砖用相同的数字来填充，不能填充的那一块，我们假定用-1来填充

来看一个输入输出样例：
利用这个输入输出样例，我们来好好分析一下这道题，这是初始化的一个正方形棋盘：

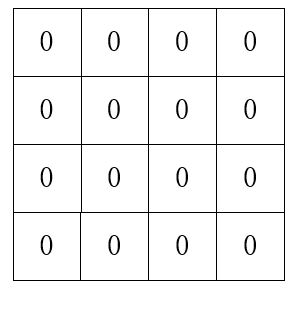
接下来，我们任意选取一个方格，用-1来填充这个方格，表示这个方格是不用覆盖的那一个。

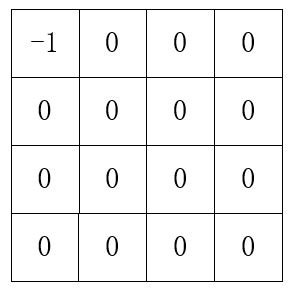
递归划分的第一次过程：
找到在哪一部分之后，对大部分平均分成四小部分。
然后把大部分中间的那四块，除了已经找到的那一部分，
剩下的三部分都填充上值v，v是递归传递的参数。
然后每次以此类推。

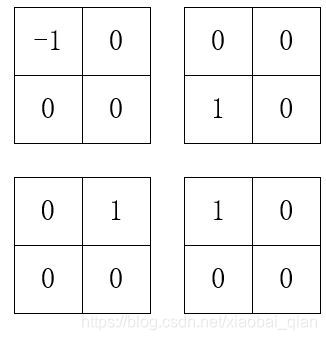
下面这个棋盘是第一次铺砖的结果，三个数字1表示，第一次铺覆盖的方格。

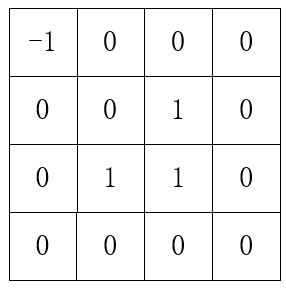
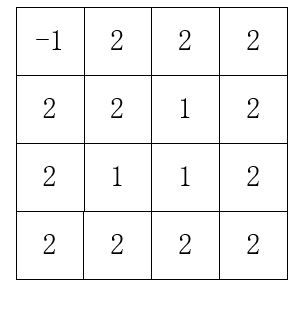
下面这个棋盘其实已经铺好了，用2填充的方格，表示第二次覆盖的方格。很明显 用2覆盖的方格它们也都是L-型的，是可以用L-型砖来覆盖的。

然后，我们再来看一下代码，因为我在写代码的过程中，二维数组不会传递参数/(ㄒoㄒ)/~~，所以写了一个类，里面有三个属性，然后用一维数组来完成这个题目。つ﹏⊂

#include<iostream>
using namespace std;
int N;    //所有的方块数量
int n1;   //全局变量边长

class A  //每一个方块是一个类
{
    public:
    int x;//方块的横坐标
    int y;//方块的纵坐标
    int key;//方块中填的值
};

void fun(A a[],int n,int x1,int y1,int x2,int y2,int v)
{
    //x1,y1递归部分的起始坐标
    //x2,y2递归部分的终止坐标
    int m=0; //判断不需要覆盖的那一块在哪一部分，左上m=1,右上m=2,左下m=3,右下m=4,
    for(int i=0;i<N;i++) //在递归的部分找到不需要铺的那一块在哪一部分，或者已经铺好的在哪一部分
    {
    if(a[i].x>=x1&&a[i].x<=x2&&a[i].y>=y1&&a[i].y<=y2)
    {
        if(a[i].key!=0)
        {
            if(a[i].x<n/2+x1)//在左边部分
            {
                if(a[i].y<n/2+y1)//左上
                    m=1;
                else//左下
                    m=3;
            }
            else//在右边部分
            {
                if(a[i].y<n/2+y1)//右上
                    m=2;
                else//右下
                    m=4;
            }
            break;
        }
    }
    }
//找到在哪一部分之后，对大部分平均分成四小部分。
//然后把大部分中间的那四块，除了已经找到的那一部分，
//剩下的三部分都填充上值v，v是递归传递的参数。
//对应上图的第3张棋盘图，然后每次以此类推。
    if(m==1) //不需要铺的那一块在第一部分的情况
    {
        for(int i=0;i<N;i++)
        {
            if(a[i].x==n/2+x1&&a[i].y==n/2-1+y1)
            {
                a[i].key=v;
            }
            if(a[i].x==n/2-1+x1&&a[i].y==n/2+y1)
            {
                a[i].key=v;
            }
            if(a[i].x==n/2+x1&&a[i].y==n/2+y1)
            {
                a[i].key=v;
            }
        }
    }
    if(m==2) //不需要铺的那一块在第二部分的情况
    {
        for(int i=0;i<N;i++)
        {
            if(a[i].x==n/2-1+x1&&a[i].y==n/2-1+y1)
            {
                a[i].key=v;
            }
            if(a[i].x==n/2-1+x1&&a[i].y==n/2+y1)
            {
                a[i].key=v;
            }
            if(a[i].x==n/2+x1&&a[i].y==n/2+y1)
            {
                a[i].key=v;
            }
        }
    }
    if(m==3) //不需要铺的那一块在第三部分的情况
    {
        for(int i=0;i<N;i++)
        {
            if(a[i].x==n/2-1+x1&&a[i].y==n/2-1+y1)
            {
                a[i].key=v;
            }
            if(a[i].x==n/2+x1&&a[i].y==n/2-1+y1)
            {
                a[i].key=v;
            }
            if(a[i].x==n/2+x1&&a[i].y==n/2+y1)
            {
                a[i].key=v;
            }
        }
    }
    if(m==4) //不需要铺的那一块在第四部分的情况
    {
        for(int i=0;i<N;i++)
        {
            if(a[i].x==n/2-1+x1&&a[i].y==n/2-1+y1)
            {
                a[i].key=v;
            }
            if(a[i].x==n/2+x1&&a[i].y==n/2-1+y1)
            {
                a[i].key=v;
            }
            if(a[i].x==n/2-1+x1&&a[i].y==n/2+y1)
            {
                a[i].key=v;
            }
        }
    }

    if(n!=2)//当n的规模不是2，就把当前规模分为四部分，进入下面的递归
    {
        v++;
        n=n/2;
        fun(a,n,x1,y1,x1+n-1,y1+n-1,v);//左上部分的递归
        fun(a,n,x1+n,y1,x1+n+n-1,y1+n-1,v);//右上部分的递归
        fun(a,n,x1,y1+n,x1+n-1,y1+n+n-1,v);//左下部分的递归
        fun(a,n,x1+n,y1+n,x1+n+n-1,y1+n+n-1,v);//右下部分的递归
    }
}
int main()
{
    int n;
    int v=1;    //方块第几次递归被铺上时的值
    cout<<"请输入方块的边长n(其中n=2^k)：  ";
    cin>>n;
    n1=n;
    N=n*n;
    A a[n*n];
    int k=0;
    for(int i=0;i<n;i++)//棋盘的初始化，对应上面的第一张棋盘图
    {
        for(int j=0;j<n;j++)
        {
            a[k].x=i;
            a[k].y=j;
            a[k].key=0;
            k++;
        }
    }
    a[0].key=-1;   //可以任取一块置为-1，表示这一块不需要铺
    //这里选取的是第一块，对应上面的第二张棋盘图
    fun(a,n,a[0].x,a[0].y,a[N].x,a[N].y,v);
    for(int i=0;i<N;i++)//输出部分
    {
        cout<<a[i].key<<"\t";
        if((i+1)%n==0)
            cout<<endl;
    }
    return 0;
}

再来给你们看一下，其他输入的输出结果：

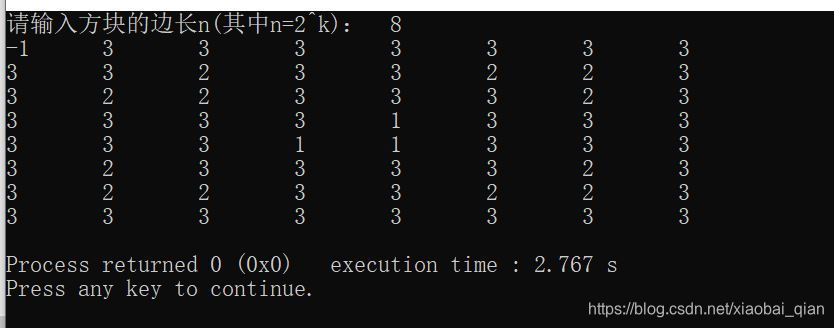
怎么说呢，我自己都没想到我可以写出来，可能是因为懒吧，拿到题目就想去网上搜一下，看别人怎么写的，可是这次我都没有找到，难为死我了/(ㄒoㄒ)/~~

你看我都可以写出来，所以你一定要相信，你也可以写出来的，说不定你会用更简单，更少的代码来解决，那你一定要给我留言哦。